离心泵快速启动过程仿真与优化
2021-07-31唐爽王彦伟刚鹏
唐爽,王彦伟,刚鹏
(武汉工程大学 机电工程学院,湖北 武汉430074)
离心泵广泛应用在日常生活和工业生产中,具有转速高、体积小、重量轻、效率高、流量大、结构简单、性能平稳、容易操作和维修等优点[1]。离心泵基本长时间在稳定工况下运行,对应的输送工况也相对较稳定。在稳定工况下离心泵运行转速或负载基本不变或者变化不很明显。当前离心泵输送性能和内部流动特性的研究主要集中在稳定工况下,对启动、停机等瞬态过程中离心泵本身的内部特性研究较少,尤其缺少对快速启动过程中水泵外特性的研究。离心泵外特性是以流量为变量、其他各参数随流量改变而变化的曲线,离心泵快速启动过程是指离心泵从停机状态到达稳定状态。
在研究离心泵快速启动过程的瞬态性能方面,王乐勤等[2-3]对泵的瞬态操作过程进行理论分析、数值模拟和实验研究,尤其是对启动过程做了大量的研究工作。LEFEBVRE等[4-6]在离心泵工况发生瞬态变化时进行试验,得出离心泵的瞬态特性与准稳态假设不合。其次,离心泵叶轮的仿真中发现实际测量的值与理论计算的值也有较大的出入[7-8]。
离心泵在快速启动的过程中转速到达最大值时,扬程也随之到达最大值,流量到达稳定状态受管道阻力的影响,转速上升与管道的阻力没有很大无关,在转速到达最大值后,瞬态性能与稳态性能基本对应,而离心泵在快速启动过程中转速的上升规律基本取决于动力源自身特性,与工况点基本无关。离心泵快速启动的水力特性对于系统能否正常运行起着决定性的作用,这个过程中离心泵的转速、流量、扬程随着时间的变化而变化,且瞬态工作下的汽蚀特性也直接左右着系统的正常运行。因此很有必要建立专用的适合于离心泵快速瞬变过程的性能测试台。
一般离心泵的设计和使用,基本参考稳态过程的研究结果,但随着对离心泵使用要求的提高以及管路系统的复杂化,特别是在舰艇武器发射装置和其他含有涡轮泵的管路系统上,要求泵在快速启动过程中起到推动武器发射等决定性作用。这个瞬态过程需要满足一定的性能要求,因此研究离心泵快速启动过程中的特性,比较其与稳态水力特性的区别,采用合适的计算方法预测动态过程将具有重要意义。此外应用Flowmaster软件搭建离心泵运行模型,根据实际测量参数设置边界条件进行仿真并与试验结果进行对比,在可信的情况下,针对离心泵不同的启动方式进行仿真分析对比验证了星-三角启动的优点[9]。
目前对复杂系统的控制策略的研究更多是建立数学模型,并运用Simulink进行仿真验证。这样研究者将花更多的精力在系统的建模上,增加了研究人员的工作量,很可能因为系统所建立的数学模型与实际系统存在很大的差异,直接影响研究结果的真实性[10]。采用实验来验证动力源特性对离心泵转速与流量等外特性的影响,操作复杂且需要付出大量的时间和经济成本,通过成熟的仿真工具模拟仿真能有效地解决这一问题。此前对离心泵的仿真应用主要集中在阀门开度和管道阻力对离心泵外特性的影响,尚未有通过Flowmaster与Simulink联合仿真来分析离心泵的快速启动过程。文中运用一维流体仿真软件Flowmaster模拟离心泵的测试平台,在Simulink中构建直流电机闭环PI调速的仿真模型作为动力源,建立Simulink和Flowmaster联合仿真的平台,为探究离心泵快速启动过程创造了条件。
1 模型构建
离心泵测试台由水箱、泵、阀门、管道、动力源和其他检测设备构成。离心泵的结构并不非常复杂,但泵中液体的运动规律非常复杂,目前为止很难做到用纯理论的方法准确的析出离心泵在不同工况下的性能,而离心泵仿真是以理论公式和经验数据为参考,具有较高的可信度。离心泵在快速启动过程中存在瞬态行为,这一过程是在极短的时间内发生的,即使是实验装置也很难准确测量该过程中的外特性,往往会由于测量环境、检测设备精度等原因使结果产生误差。离心泵的动力源特性,虽然能够在出厂时得到,但加上离心泵作为负载后,其复杂的内流特性难以确定分析。因此很有必要建立联合仿真模型来分析离心泵的动力源特性在快速启动过程中的瞬态行为。
1.1 离心泵测试模型
Flowmaster中管网模型是由各种管道元件所组成,其计算原理是基于质量流量与进出口压力得出。管道与各种元件的相互连接,通过质量守恒定律和能量守恒定律导出的线性化方程来描述管网中元件内介质的流动。可以看作是将模型中的每个管道与每个元件都当作单独的阻力部件,其中各种水泵相当于负作用阻力部件,管道与阀门等都是正阻力部件,因此可以依据流过部件的实际流量,作用压力等因素计算出元件的阻抗大小。所以模型的计算可以转化为求解一组单独的线性化方程组,计算出方程组就能得到质量、流量和进出口压力。加上其他条件就能求得密度、流速等参数。
Flowmaster元件库中有丰富的泵类、管道等组件满足大部分用户的需求,能较好地实现对离心泵测试台的仿真。
如图1所示,元件3和4长5 m,直径为40 mm。元件8的标题名称应与Simulink中模块标签和名称一致且标签为全局可见。离心泵额定流量0.069 m3/s,额定扬程52 m,额定功率3.5 kW,初始速度0 r/min。一般可通过Pro/E的模型分析菜单,计算出各种材质离心泵所对应的转动惯量。Flowmaster中离心泵的转动惯量有自己的计算公式,算得离心泵转动惯量为0.00079 kg·m3,电机转动惯量0.00252 kg·m3。为提高仿真精度,尽量减少仿真过程中的数据与实际测量数据的误差,需自定义离心泵的流量扬程曲线,将稳态工况下的离心泵实际测得的数据拟合成离心泵的流量扬程特性曲线添加至泵参数中。

图1 Flowmaster离心泵测试台网络模型
1.2 直流电机模型
离心泵泵轴与电机的连接方式有固定连接、直接连接和法兰式电动机连接。本文选用有刷直流电机作为离心泵测试系统的动力源,以下简称直流电机,其连接方式为直接连接,依据离心泵的轴功率计算出直流电机的配套功率为4.26 kW。基于等效电路构建直流电机的仿真模型,它的结构简单,便于调速控制,该仿真模型由机械部分和电气部分构成,电气部分由电枢电路、机械部分由电磁转矩和电枢电势构成[11],相关计算如下:

式中:U为电机电动势,V;Ea为电枢电势,V;i a为电枢电流,A;Ra为电枢绕组,Ω;La为电枢电感,H;t为时间,s;Te为电磁转矩,N·m;K T为MATLAB提供的直流电机模型中额定励磁下的转矩电流比,N·m/A;J为电机转动惯量,kg·m2;ω为输入转速rad/s;TL为负载转矩,N·m;K E为电机结构确定的一个常数,V/rad·s。
当电枢在磁场中转动时,线圈产生感应电势,由于电枢电势与电流或者外加电压方向相反,也称反电动势。
由以上的数学关系可以得到直流电机的仿真模型,通过输入相同参数与Simulink库中DC Machine模块对比,直流电机的动态响应基本一致,验证了构建的直流电机仿真模型的正确性。引入PI控制可以得到直流电机闭环PI调速仿真模型[12],如图2所示。

图2 直流电机闭环PI调速仿真模型
1.3 PI参数整定
PI参数整定的方法主要有理论计算整定和工程整定,前者通过确定的数学模型计算出最优的整定参数,后者主要依据工程经验,通过输入参数得到特征量,经过查询经验表得到最佳控制参数。
常用的工程整定法衰减曲线法又称阻尼振荡法,是在只考虑比例的情况下运行使系统产生衰减振荡,得到衰减比例度δ和衰减周期T,然后依据经验总结出来的关系求出控制器的参数值[13-14]。具体操作是,首先将闭环系统的纯比例度由大逐渐调小,观察输出响应的过程,直到出现y1:y2=4:1的衰减过程为止,这时的比例度称为4:1衰减比例度,相邻波峰之间的距离为T1,由经验公式计算出参数,通过衰减曲线法,经过试验查表后适当调整得到Kp=125、Ki=499。
2 联合仿真
2.1 联合仿真模型
离心泵的驱动方式为泵轴直接连接,因此可将离心泵看作是直流电机的负载,直流电机为离心泵提供转速。图3为直流电机驱动下离心泵的仿真模型,子系统是直流电机闭环PI调速仿真模型。其中From模块和Goto用于接收Flowmaster与Simulink间的交互信号。配置联合仿真接口需要选分析类型为Incompressible Transient。

图3 联合仿真模型
如图4所示,离心泵在快速启动过程中转速在0~0.8 s间到达稳定状态。启动初期,离心泵作为电机的负载较小,管道内的液体呈静止状态。随着液体的流动,管道内阻力变大,加上流量上升使电机负载变大,电机转速随之下降,当负载扭矩上升到趋于稳定,电机转速也趋于稳定。离心泵的流量在1 s左右趋于最大值,流量达到稳定状态的时间滞后于转速达到稳定状态的时间。其中转速在快速启动过程中超调量过大,容易产生扬程冲击,影响离心泵的使用寿命。
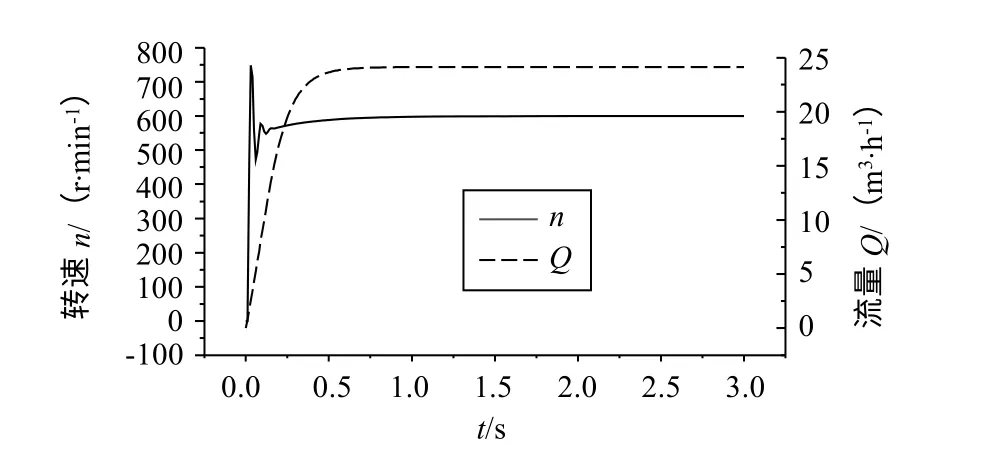
图4 离心泵流量与转速
2.2 仿真优化
使用闭环PI控制的直流电机作为动力源,离心泵在快速启动过程中超调量较大,因此有必要对直流电机的控制方法进行优化。由PI控制器各个环节的作用可知,比例控制作用动态响应快,积分控制能消除静态误差,但动态响应慢,PI控制器的积分作用从理论上可以使系统的稳态误差到达零,但时间上较为滞后。在传统的控制系统中,必须有数学模型,而模糊控制是基于用语言描述的经验规则,并不基于准确数学模型[15],它是以人的经验和知识为依据运用模糊推理机制的控制方法。模糊控制具有实现简易性和快速性的优点,一般采用二维的模糊控制,这类控制器都是以系统偏差和偏差变化率作为输入,可以获得良好的动态特性,其能有效地消除稳态误差,有关学者提出模糊控制和PI调节控制结合的思路[16]。
如图5所示,依据Simulink中模糊控制模块帮助文件中非线性面模糊控制器编写m文件,构建模糊推理系统为:

图5 加入模糊PI控制的直流电机调速模型

Sugeno型模糊推理系统运用了反向传播下降梯度法与最小二乘法相结合的方法,Gaussmf为高斯曲线隶属度函数。
2.3 优化结果分析
由图6可知,在模糊PI控制下,流量提前0.2 s到达稳定状态,这对离心泵在特殊场合的应用具有重要意义。

图6 模糊PI控制下离心泵流量曲线
由图7可知,模糊PI控制下,离心泵转速的稳态误差较小,超调量有明显减小,动态响应快慢基本一致,且更快到达稳定状态。这是因为非线性控制面的模糊PI控制器在误差较小时更快地减小误差,当误差较大时,控制器变得不那么主动从而限制了控制动作。
3 总结
本文对直流电机驱动离心泵快速启动过程进行仿真,由仿真结果可看出,离心泵流量和转速到达稳定状态的过程与离心泵配套的动力源特性有直接关系。改变动力源特性,通过优化直流电机控制参数,离心泵流量到达稳定状态的时间有所提前,转速超调量变小,离心泵性能得到优化。此外构建的联合仿真模型可以后续用来分析离心泵扬程、出口压力、功率等外特性曲线。且仿真模型的互换性较好,相比实验测试,更加方便快捷,为离心泵的设计提供了参考。
图7 模糊PI控制下离心泵转速曲线
