基于轴箱加速度时频域特征的车轮多边形故障识别

2021-07-31陈翔宇樊懿葳李凤林

机械 2021年7期

陈翔宇，樊懿葳，李凤林

（成都运达科技股份有限公司，四川成都611731）

铁道车辆的车轮多边形化会严重影响车辆的运行安全、运行品质和部件的使用寿命。1998年，因车轮多边形化导致的轮辋疲劳裂纹，德国ICE列车发生严重事故，造成101人死亡和194人受伤[1]。车轮多边形引起的轮轨冲击会增加轴箱盖和制动盘的螺栓断裂风险[2]；车轮多边形会导致噪声和振动水平提高、运行品质降低，使乘客感到不适，特别是在特定车速下[3]；车轮多边形会增加轮轨垂向接触力，从而导致疲劳并缩短轨道和车辆零部件（例如轮对轴承、齿轮箱、螺栓、紧固件）的使用寿命[4]。

检测车轮多边形目前有三种较为常用的方法，一是采用车轮粗糙度测量系统，但该系统需在检修库内离线运行，对车辆的正线运营会造成一定影响；二是基于轨旁设备检测出垂向轮轨力进而推导出车轮多边形，但该方法的精度受车轮直径、轨枕间距和地面传感器布置的影响较大[5]；三是基于轴箱振动加速度进行检测，该方法信噪比高、可在线实时监测车轮多边形，是三种方法中可行性最高的方案[6]。

本文以HXD1型和谐电力机车为研究对象，建立了考虑轮对柔性和车轮多边形的刚柔耦合动力学模型，对受车轮多边形影响的轴箱加速度信号的时域特征、频域特征进行了说明，并利用时频特征与车轮多边形之间的关系提出一种车轮多边形故障诊断流程，该流程可以诊断出车轮多边形的阶数以及车轮多边形是否达到镟修标准。

1 动力学模型

1.1 刚柔耦合动力学模型

在SIMPACK中建立HXD1型机车的刚体动力学模型[7]，再导入柔性轮对替换刚性轮对，得到车辆刚柔耦合动力学模型[8]如图1所示。

图1 HXD1机车动力学模型

1.2 车轮多边形模型

HXD1机车车轮多边形一般存在一个低阶的多边形和高阶的多边形，低阶以一阶为主[9]，高阶多集中在16～24阶[10-11]。某机务段对段属HXD1型和谐机车的1088个车轮的多边形分布情况的统计结果[12]如图2和图3所示，统计范围包括16～20和24阶多边形。

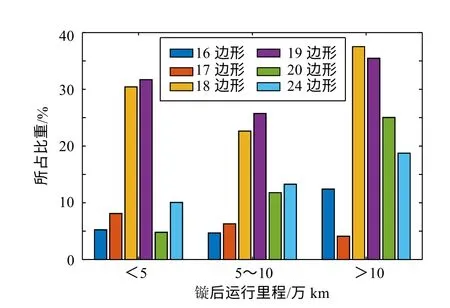
图2 多边形阶次分布图

图3 车轮径跳值分布图

由图2可知：

（1）当镟后里程分别为0～5万km、5～10万km和10万km以上时，60.8%、47.1%和71.6%的车轮都出现了18或19阶多边形，这说明在任何阶段HXD1车轮的18、19阶车轮多边形都十分普遍。

（2）三个阶段出现高阶多边形的概率分别为90.4%、84.4%和133.3%，说明镟后里程小于10万km时大概率会出现高阶多边形，大于10万km时会同时出现多个多边形阶次。

由图3可知：

（1）车轮的多边形化是一个发展的过程，随着运行里程的增加，车轮的多边形磨耗深度会逐渐加深。

（2）当镟轮后运营里程分别为0～5万km、5～10万km和10万km以上时，径跳值小于0.2 mm的概率分别为94%、81.3%和64.3%，设定径跳值阈值为0.2 mm能有效区分出多边形化车轮与非多边形化车轮。

（3）机务部门通常以车轮的径跳值来判断车轮多边形的严重程度以及是否达到镟修状态，一般认为车轮的径跳值超过0.2 mm时车轮已达到镟修临界状态，结合图3数据可以发现，设定径跳值阈值为0.2 mm完全符合车轮多边形的发展规律，因此本文规定的镟修标准为车轮径跳值不能超过0.2 mm。

综上所述，HXD1机车的高阶多边形化现象十分普遍，18和19阶尤其突出；设定径跳值报警阈值为0.2 mm可以有效区分HXD1机车的多边形化车轮与非多边形化车轮。

以18阶和19阶占主导地位的多边形车轮为例，随机拟合1～40阶多边形的幅值Ai和相位φi，使用1～40阶谐波的傅里叶级数形式的位移函数来描述车轮多边形[13]：

式中：v为车辆运行速度，m/s；R为车轮半径，m；t为时间，s；Z0为随时间变化的车轮径跳值，mm。

得到临修状态的车轮多边形样本如图4。

图4 车轮多边形样本

图4（a）中18阶的粗糙度幅值最高，为38.03 dB，车轮径跳值为0.20094 mm；图4（b）中19阶的粗糙度幅值最高，为36.31 dB，车轮径跳值为0.2 mm。

2 轴箱加速度时频特征

2.1 频域特征

将上述车轮多边形样本以Input function的格式导入图1所示动力学模型中。设定车速分别为40～120 km/h，得出轴箱垂向加速度的频谱图如图5所示。

轮对的柔性模态信息如表1所示。

表1 轮对柔性模态信息

由图5和表1可知：

图5 轴箱加速度频谱图

（1）车轮发生多边形化时，在频谱一般会出现若干个主频，并且在转频倍频位置会出现转频倍频的边频带。

（2）轮对的柔性模态集中在60～120 Hz的频率范围内，当转速倍频与轮对柔性模态接近时，容易引发轮对的柔性模态共振。如图5（a）所示，在车速为60 km/h时，18阶多边形特征频率为76.4 Hz，接近轮对一阶垂弯频率74.28 Hz，说明18阶的车轮多边形激发了轮对一阶垂弯共振，导致轴箱加速度幅值迅速增大。

（3）非主导地位的多边形阶次也可能激发轮对柔性模态共振，如图5（a）所示，70 km/h时，频谱响应幅值最高频率是17倍转频84.2 Hz，非常接近轮对构架耦合共振频率84.3 Hz，由图4（a）可知17阶并非车轮多边形的主导阶次，但17阶对应频响幅值最高，这说明了17阶转频边频激起了轮对柔性模态共振。如图5（b）所示，70 km/h时频谱响应幅值最高的频率是16倍转频79.2 Hz，正好对应车轴的一阶横弯频率79.2 Hz，而由图4（b）知，16阶并非该条数据的多边形主导阶次，这说明16阶的车轮多边形激发了轮对一阶垂弯共振，导致轴箱加速度幅值迅速增大。

由以上结论可知，多边形化的车轮的频谱图有以下特点：频谱能量集中在转频倍频附近；频谱最大幅值出现在主导多边形阶次频率或与模态特征频率接近的转频倍频频率；因此可以利用这些特点对多边形故障特征进行识别。

2.2 时域特征

HXD1车轮的高阶多边形多集中在16～24阶，前文只制作了18和19阶的多边形样本，为了完善仿真数据库，制作了分别由16、17、20和24阶多边形占主导地位，各样本的径跳值均为0.2 mm的车轮多边形样本如图6所示。

图6 车轮多边形样本

将各阶次车轮样本导入到动力学模型中，得到对应的轴箱加速度，16阶样本在100 km/h时对应的轴箱加速度时域及时域包络信号如图7所示。对信号时域谱求有效值可以描述信号的能量特征；对信号的包络谱求峭度值可以描述信号的突变程度。

图7 轴箱加速度时域响应

分别导入16～24阶的车轮多边形样本，选取仿真速度区间为40～100 km/h，仿真数据库中包含了40～100 km/h共7级速度，16、17、18、19、20和24阶共6级多边形阶次，共计42组工况的数据，统计不同样本在各级速度下的有效值如图8所示，图中数据如表2所示。

表2 不同阶次的轴箱加速度有效值

图8反映了轴箱振动能量随车速和车轮多边形阶次的变化情况，当车速在60～90 km/h时，16～24阶多边形的激振频率为67.9～152.8 Hz，正好对应表1中轮对柔性模态范围，因此可推断，轮对柔性共振对轴箱加速度有效值影响较大，主要影响的速度区间为60～90 km/h。

统计不同阶次样本在各级速度下的包络谱峭度值如图9，数据如表3所示，一般正常轴箱振动信号的峭度为5左右，故障振动信号的峭度一般大于5，由表3可知，多边形故障下的仿真数据峭度值大多都在正常范围内，说明仿真数据与实际加速度信号波形较为类似。

由图9可见，在60～90 km/h的速度区间下，轴箱加速度的峭度值随着速度的变化程度不明显，这说明多边形故障与轮对的柔性模态共振并非冲击信号，时域信号突变程度不大。

由以上分析可知，有效值指标对多边形故障与轮对的柔性模态共振更为敏感，更能全面地描述多边形故障随车速和多边形阶次的变化情况，因此有效值指标的权重值更高，为0.8，包络谱峭度值的权重比为0.2。以图8和图9所示的轴箱加速度有效值和包络谱峭度乘以各自的权重系数再相加作为诊断阈值。

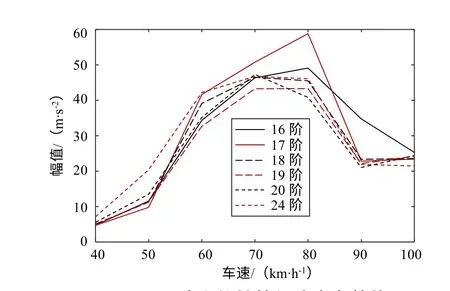
图8 不同阶次的轴箱加速度有效值

图9 不同阶次的轴箱加速度包络谱峭度值

导入机车的实测轴箱加速度数据，当得知实测轴箱数据有高阶多边形故障（16～24阶）特征后，由识别出的主导多边形阶次和车速等信息便可插值计算出有效值阈值和包络谱峭度阈值。以同样的方法计算出实测信号的有效值和包络谱峭度值，并乘以各自的系数作为计算值。当实测轴箱加速度的计算值大于诊断阈值时，即认为车轮径跳值超过了0.2 mm，车轮已达到镟修标准。例如实测数据的多边形阶次为18阶，数据样本的车速为67 km/h，根据插值结果，其有效值阈值为45.83 m/s2，包络谱峭度阈值为2.12 m/s2，诊断阈值为37.09 m/s2，当实测数据的计算值超过37.09 m/s2时，即可认为车轮已达镟修标准。

3 车轮多边形故障识别

3.1 多边形故障诊断流程

根据时域与频域分析结果，提出车轮多边形故障诊断流程，如图10所示。

图10 多边形故障识别流程图

（1）当轴箱加速度满足40～100 km/h的速度区间要求，且数据不存在干扰时，采用数据，否则弃用数据；

（2）对加速度做FFT得出频谱图，在频域上对多边形故障特征进行识别；

（3）计算出信号的时域有效值和时域包络谱峭度值，乘以各自权重后与诊断阈值相比较，若小于诊断阈值则认为该条数据车轮多边形不明显，若大于等于诊断阈值则说明该车轮对应的多边形已达到镟修标准。

3.2 多边形故障特征识别子流程

图10中的多边形特征识别子流程如图11所示。

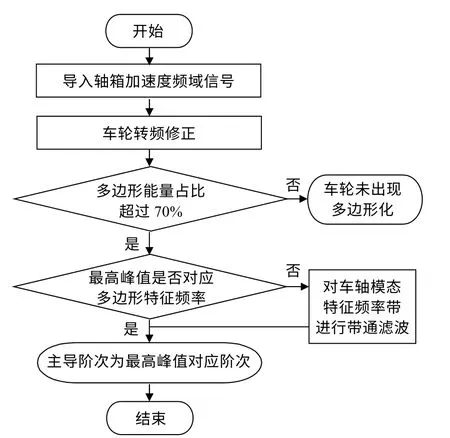
图11 多边形阶次识别子流程图

车轮的转频为：

式中：0f为车轮转频，Hz；V为车速，km/h；D为车轮滚动接触圆的直径，m。

多边形故障特征频率为f0的倍频。但由于各车轮的D值各不相同，各车轮的f0也略有不同，f0的取值对多边形的特征识别有很大的影响，因此有必要对f0进行修正。以f0的1～40倍为中心频率，以f0的0.05倍为搜索半径，若搜索范围内幅值最大的频率落在频谱前5大波峰值上的次数大于等于4次，则以前4大波峰值频率对应的基频的平均值重新修正f0。

振动信号为离散信号，其能量计算公式为：

式中：xi为离散振动信号的加速度值，m/s2；N为各离散信号对应的序号。

以修正后的f0的1～40倍为中心频率，以f0的0.15倍为搜索半径，分别计算多边形倍频段的频谱能量E p和信号样本整体的频谱能量E，E与E p的比值即为多边形能量占比。当多边形能量大于70%，则说明频谱能量集中在转频倍频附近，车轮多边形化现象明显。

4 实测数据验证

在某机务段HXD1型机车各轴箱测点布置原始振动数据采集传感器，采集到第4轴右侧轴箱的原始振动数据，如图12所示。

图12 原始轴箱振动加速度（车速52.6609 km/h）

先按照图11对该条数据进行多边形阶次识别：采集该条数据时对应车速为52.66 km/h，满足速度区间要求。未磨耗车轮直径为1.25 m，根据式（2）计算得出f0＝3.7249 Hz，修正后，f0＝3.7248 Hz。据式（3）计算出该条数据多边形故障的能量占比为84.69%。频谱主频对应频率63.33 Hz，63.33/5.3771＝17.0023。综上可判定，车轮出现了明显的17阶多边形。

然后按照图10对该条数据进行多边形深度诊断：由图8和图9的数据插值可得，该条数据对应的加速度有效值阈值为44.0810 m/s2，包络谱峭度阈值为3.1071，因此整体的诊断阈值为35.8862；对时域原始数据进行计算，得出加速度有效值为7.2205 m/s2，包络谱峭度阈值为3.3106，因此诊断指标值为6.4385，指标值远小于诊断阈值，说明该车第4轴右侧车轮出现了17阶多边形但其多边形深度未达0.2 mm，车轮多边形故障仍处于发展初期阶段。