巧添辅助线计算组合图形的面积

文|陈仲琼

在解决组合图形面积时经常用到添辅助线的方法，如何借助辅助线让组合图形面积的计算更有效，可以这样设计教学过程。

1.通过添辅助线将不规则图形分割成规则图形。

出示图1，要计算这个图形的面积，你需要先做什么？通过添辅助线，将其分割成学过的图形。学生独立在图中添辅助线，然后和同桌交流添了哪一条，分割成哪些基本图形。讨论得出四种不同的添辅助线的方法。

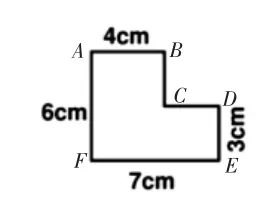
图1

思考：添怎样的辅助线对解题有帮助？让学生理解有效地添辅助线需要满足两个前提条件：第一，将不规则图形分割成已学过的图形；第二，分割成的每个图形都拥有完整的解题数据。

2.在添辅助线的基础上利用等积变形解决问题。

出示图2，ABCD 是直角梯形，∠B是直角，AB 长3cm，BC 长6cm，求阴影部分的面积。要解决这个问题，你现在遇到什么困难？你打算在哪里添辅助线？添几条？让学生明白，这里只能连出两条辅助线：连接AC 或连接BD。

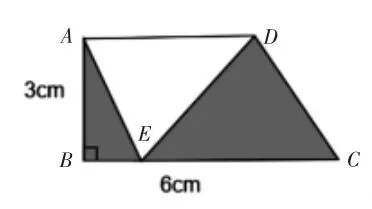
图2

思考：这两种都添了一条辅助线，哪种可以解决问题呢？为什么？根据讨论，得出解题思路。让学生体会到：添辅助线可以有不同的添法，不同的添法都可以解决问题。

3.在多条辅助线中找出可以解决问题的辅助线。

出示图3，求阴影部分的面积。

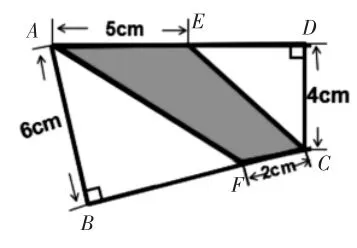
图3

思考：可以添几条辅助线？预设：⑴连接AC；⑵连接BD；⑶连接DF；⑷连接BE。追问：每种添辅助线的方法是否都可以解决问题？为什么？经过讨论，发现只有其中一条可以轻松解决问题,其他三条辅助线都不能帮助求出阴影部分面积。得出解题思路：连接AC，把阴影部分拆分成三角形AFC 和三角形AEC，并且这两个三角形拥有完整的解题数据。让学生体会到：添加辅助线不是越多越好，关键的辅助线才对解题有帮助，过多的辅助线反而会干扰解题。