小学生推理能力培养的三个阶段

文 唐少雄

《数学课程标准（2011年版）》明确指出：“推理能力的发展应贯穿在整个数学学习过程中。推理是数学的基本思维方式，也是人们学习和生活中经常使用的思维方式。”推理作为学生数学学习的一个基本能力，受到了空前的重视。早在2001年的实验版课标中就把“推理能力”列为六个核心词语之一，2011年版的课标更是赋予“推理能力”全新的解释，并明确了推理能力的教学价值与目标要求。逻辑推理是高中学生发展的六大核心素养之一，进一步明确了推理能力的学科地位和价值取向。可见，小学数学应把学生推理能力的培养和发展作为教学的出发点和归宿，贯穿在学生数学学习的全过程。推理是学生学习的基本能力，是学生数学学习的基础和保障，是重要的学习方法和数学思想，教师应重视学生推理能力的培养和发展。

一、小学生推理能力培养的总体目标

从基本内涵看，逻辑推理是指从一些数学已有的事实和命题出发，依据规则推出其他的事实和命题。一般包括合情推理和演绎推理。合情推理是从已有的事实出发，让学生凭借知识经验和数学直觉，通过归纳和类比等推断其他的数学事实；演绎推理是从已有的事实（包括概念、规律和性质等）和确定的规则（包括运算的定义、法则、顺序等）出发，按照逻辑推理的法则加以证明。小学阶段以合情推理为主，演绎推理为辅，把对学生推理能力的培养贯穿于学生整个学习过程，在解决实际问题中，这两种推理经常相辅相成、合二为一。合情推理用于探索思路，蕴含在学生的数学探究中，引导学生在操作中发现结论；演绎推理则用于一些简单的数学证明。合情推理的基本形式有归纳、类比，是一种从特殊到一般的推理；演绎推理则是从一般到特殊的推理，借助一般的数学事实推导出其特殊性，并加以证明。

《数学课程标准（2011年版）》对学生推理能力的培养有具体明确的目标要求，在第一学段中要着力培养学生“在观察、操作等活动中，能提出一些简单的猜想”“会独立思考问题，表达自己的想法”；第二学段则要“在观察、实验、猜想、验证等活动中，发展合情推理能力，能进行有条理的思考，能比较清楚地表达自己的思考过程与结果”“会独立思考，体会一些数学的基本思想”。从目标要求看，第一学段重在培养学生的问题意识，能结合数学活动提出猜想，关注学生创造性思维的培养；第二学段重在培养学生的合情推理能力，培养学生良好的思维习惯和创新意识。这就决定了，推理能力的发展具有一定的阶段性，每个阶段要有明确的目标要求和渗透重点。

二、小学生推理能力培养的三个阶段

在教材的编排上，人教版以《数学课程标准（2011年版）》为指导，把推理贯穿学生整个学习活动过程，从一年级上册就开始有意识地渗透推理。教材的编排思路主要是逐步渗透、螺旋上升，突显逻辑推理的阶段性和发展性，根据学生的年龄特征和思维习惯，人教版教材对逻辑推理的渗透分三个阶段，每个阶段有明确的目标要求。

第一阶段：启蒙阶段。

人教版教材对推理的渗透从一年级上册就开始了，主要的编排特征是逐步渗透，重在启发学生学会思考，培养学生良好的思维习惯。如《9 加几》一课中，由于学生之前已经在《10 的组成》中学会了凑十，而且也学会了连加的计算，这些是学生学习本课的学习基础，而“凑十法”是本课教学的重点，是正式引入推理的载体。教材以“9＋4”为例，先引导学生摆小棒进行计算，体验“接着数”的基本方法；接着，引导学生感受“凑十法”，即“9＋1＋3”的过程，这个过程是学生推理的理论基础，引导学生把4 分成“1＋3”再进行凑十；最后，形成严谨的归纳推理（如下图）。

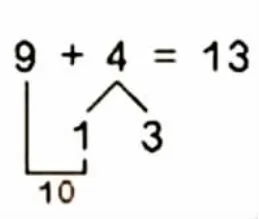
这是人教版渗透推理的雏形，也是正式引入推理的开始，比较完整地引导学生进行数学思考，学会有理有据地推理。从一般的数学思考“接着数”，到有依据地数学思考“凑十法”，重在引导学生学会思考，促进他们思维的发展，培养良好的思维习惯。像这样零散的推理在后续的“8、7、6 加几”“5、4、3、2 加几”比比皆是，这些数学思维都是“凑十法”的延续和发展，是类比推理思维形式的丰富与发展，到了一年级下册《20 以内的退位减法》更是“凑十法”的反思与推理，在“想加算减法”的基础上借助“破十法”进行退位减法，体会一般的归纳推理。一年级下册“数学广角”安排了《找规律》一课，奠定了“推理”的基础地位，让学生在找规律中体验归纳与类比的推理过程，感悟推理的基本思想，培养和发展学生的合情推理能力。

第二阶段：形成阶段。

人教版二年级下册的“数学广角”编排了独立单元“推理”，主要的编排特征是正式引入“推理”，让学生结合具体的情境，初步学会用推理的思维进行判断，学会简单的数学推理，重在感受推理的基本形式，学会有理有据地数学思考，体会推理的应用价值。《推理》一课安排了两个例题，例1 以小红、小丽和小刚三人分别拿了语文、数学和品德与生活三本书为情境，让学生在活动中体会推理的思维形式。

教学中，让学生学会从信息本身寻找解决问题的突破口，读懂信息背后蕴含的信息。首先，要从既定的事实出发。“小红拿的是语文书”这一信息是确定的，可以作为解决问题的突破口，并以此为判断依据，也可以进一步理解剩下的两本书分别是数学和品德与生活。其次，要从其他的信息寻求思路。“小丽拿的不是数学书”这一信息背后蕴藏着两条信息，一是小丽拿的不是数学书，二是剩下数学和品德与生活两本书，这两条信息是相互关联的，是进一步推理的基础和前提。最后，进行合情推理。剩下的两本书是数学和品德与生活，因为小丽拿的不是数学书，所以，小丽拿的肯定是品德与生活。那么，剩下一本数学书就是小刚拿的。在看似简单的推理中蕴含推理的基本形式，让学生明白简单推理的思维形式，能确定的要先确定，能排除的要排除，要读懂信息，还要读懂信息背后的隐藏信息。同时，在逻辑推理时，要注意适当地抽象，引导学生用形式化的语言表达，如用画图、列表等方法帮助学生梳理信息、理解信息，实现更好的推理。

例2 是例1 的丰富和发展，是在稍复杂情境中对信息的甄别与分析，培养学生寻找解决问题的突破口，从推理的角度进行思考和分析。

教材要求在16 宫格中判断B 是几，读懂基本要求“每个数在每行、每列都只出现一次”，因此要引导学生思考：哪一个空格所在的行和列出现了三个不同的数？这样就把“A 是几”作为解决问题的关键，A所在的行有了2，所在的列有了1 和3，这就有了推理的依据，A 就是4，把能确定的先确定下来。用同样的推理方式，引导学生思考B 所在的行和列各有哪些数？找到行和列有2、3、4，所以B 应该是1，接下去，让学生自己尝试推理其他的空格。教学中，要尽量引导学生学会使用“因为……所以……”“再因为……所以……”的句式表达自己的推理过程，学会有理有据地推理。

在形成阶段，教师首先要注重引导学生读懂信息，发现推理的关键信息；其次要寻找突破口，找到最先能确定的既定信息，寻找推理的重要依据；接着，尝试根据已有的信息合情推理，探寻推理的一般方法；最后，学会用一定的逻辑思维有依据地推理，形成推理的一般表达习惯，学会严谨有条理的推理过程，培养良好的思维习惯。

第三阶段：发展阶段。

人教版教材六年级下册总复习编排了“数学思考”独立内容，意在对第二学段所渗透的逻辑推理作梳理、总结和提升，为第三学段的数学探究提供思维基础和方法保障，培养和发展学生的逻辑推理能力。六年级下册总复习中的“数学思考”集中安排了四道例题，涵盖小学阶段所涉及的合情推理和演绎推理两种思维形式（见下表），这四道例题所采用的素材不一样，呈现的形式也不一样，但是其教学的内涵是一样的，都蕴含着推理的思想方法。

例1 找规律 合情推理例2 列表推理演绎推理例3 等量代换例4 简单的几何证明

这四道例题的编排思路由易及难、相互关联、相互补充，完整呈现了小学阶段的逻辑推理形式。

例1 的找规律是一年级简单找规律的高级形式，要求平面上几个点可以连多少条线段，让学生从简单入手通过寻找增加的点数和增加的线段数之间的关系，利用枚举和数列，寻找蕴含其中的数学规律，推理出点数与线段数之间的关系，是一种典型的合情推理。例2 的列表推理是对二年级推理形式的发展，从简单的列表推理到复杂情境中的列表推理，让学生通过列表，逐步缩小与A 同班的人的范围，最终确认唯一符合要求的人。让学生在列表推理中不断排除矛盾、推出必然结果的思维方式，是一种演绎推理。例3的等量代换，在之前的编排中虽有涉及，但不系统，这里结合实例帮助学生理解等量代换时，可以用一个与它相等的量去代替，它是演绎推理的基础，为第三学段解方程的方法、发展代数思想做准备。例4 是一道经典的用演绎推理来进行证明的几何题，小学阶段的数学没涉及证明，通过本例题教学可以发展学生的推理能力，积累证明的基本经验，有利于中小学教学的良好衔接。

在小学的整理和复习阶段，安排了以“推理”为主线的这几个内容，让学生系统地经历从特殊到一般的合情推理、从一般到特殊的演绎推理的过程，让学生在观察、猜想、验证等活动中，发展合情推理能力，培养学生学会有条理的思考，能比较清楚地表达自己的思考过程与结果。这样的编排有利于培养学生学会思考、独立思考，体会一些数学的基本思想，还有利于培养学生的逻辑思维，结合实例体会推理的应用价值和实践意义。