抓住本质 边“破”边“立”——《倍的认识》教学实践与反思

文|倪斌强

在一次和新思维教育科学研究院共同开展的教研活动中，我们连续听了几节《倍的认识》，课后感觉到学生学习“倍”有点困难，根本原因在哪里呢？经过与教研员的讨论，认识到主要原因有三点。

第一，认识“倍”是学生从“加法结构”到“乘法结构”的一次质的转化，而认知结构的转变是学生学习的最大困难。

第二，“倍”在刻画两个量的关系时，要从绝对数量的多少比较转变到相对数量的关系认识，这是很多学生不易想通的地方。

第三，日常的“倍”与数学上的“倍”稍有区别。日常的“倍”，商一般大于1，而数学上的“倍”，商大于、等于或小于1 都可以。

找到了学生学习“倍”的困难之处，教学中应设计哪些有效教学活动来突破学生学习的障碍呢？我们对《倍的认识》进行了重新设计，并进行实践，取得了较好的效果。

一、初步认识“倍”

1.出示题目。

第一题：说说第一行的△和第二行的○有什么关系？

图1

生：第一行比第二行少3 个。

生：第二行比第一行多3 个。

师：它们除了相差关系还有什么关系呢？这是我们这节课要研究的内容。

第二题：出示下图，要求根据前三幅图的规律，画出第四幅图第二行的图形。

图2

图3

图4

2.反馈交流。

师：说说你是怎么想的。

生：我画了8 个☆，因为第一行几个，第二行就比它多几个。

生：我画了8 个□，第一行的个数乘2 就是第二行的个数。

师：如果把第一幅图中第一行三个△看为一份（边说边圈），那么第二行有这样的几份？

生：2 份！

师：另外几幅图，像老师这样圈一圈，看看是不是都一样。

（学生动手圈画）

师：比较这几幅图有什么共同点？

生：都是第一行的个数为一份，第二行的个数有这样的两份。

师：那我们就可以说：第二行的个数是第一行的2 倍。

师：按“（ ）为一份，（ ）有这样的（ ）份，（ ）是（ ）的2倍。”说一说。

3.提炼。

师：每组图的东西不一样，个数也不一样，为什么都可以说第二行的个数是第一行的2 倍呢？

生：因为都是以第一行的个数为一份，第二行都有这样的两份。

师：对啊，不管什么物体，有几个，只要以第一行为一份，第二行有这样的两份，都可以说第二行的个数是第一行的2 倍。

【设计意图：1.课始出示第一行3 个△和第二行6 个○的图片，让学生说说第一行的△和第二行○的关系，学生说出相差关系后，教师引导学生说“除了相差关系还有什么关系呢？”打破学生的认知平衡（相差关系），激发学生学习的兴趣（除了相差关系还有什么关系），为“破”加法结构“立”乘法结构做好了准备。2.学生根据前三幅图画图时已初步体会到“倍”的结构，也就是第一行都有一份，第二行都有这样的两份。引出“倍”后，再让学生异中求同——“每组图东西不一样，个数也不一样，为什么都可以说第二行的个数是第一行的2 倍呢？”这样逐步剥离“倍”的非本质属性（与是什么物体、个数有几个无关），显现倍的本质特征——只要以第一行为一份，第二行有这样的两份，都可以说第二行的个数是第一行的2 倍。】

二、着力构建2 倍

1.课件把物体隐去，留下第一行一个圈圈，第二行两个圈圈。

师：这两样比较的东西除了作业纸上的这些，还可以是什么？

生：还可以是铅笔、书本、男生、女生……

师：个数除了1、2、3、4，还可以是几个？

生：5、6、7、8……

2.画一画。

要求：画的两种量，一种量是另一种量的2 倍。并且尽量画得与众不同。

3.反馈交流。

（1）出示学生的各种画法。

（2）比较这些图：为何都可以说一种物体是另一种物体的2 倍？

4.提炼。

师：只要一种物体的个数为一份，另一种有这样的两份，都可以说两份的物体个数是一份物体个数的2 倍。

师：一份的如果是20 个、50个、100 个，两份的分别是多少？

师：一份的如果是a 个，那么两份的有多少个？

生：b 个。

师：很好，能用字母来表示，但b 个能看出有这样的两份吗？

生：不能。

师：那到底怎么表示呢？

生：2 个a。

【设计意图：1.由于要求画得不一样，学生就会存同求异，出现了以第二行为标准量、不工整排等几种变式情况，也就“破”了一定以第一行为标准量的思维定势，更好地建立了“2 倍”的模型。然后又进行了异中求同的比较——“为何都可以说一种物体是另一种物体的2 倍”，使学生明白“只要一种物体的个数为一份，另一种有这样的两份，都可以说两份的物体个数是一份物体个数的2 倍”。2.“一份的如果是a 个，那么两份的有多少个？”尝试在三年级就渗透用字母表示数，让学生体会符号的含义。经过实践，学生完全能够接受，一开始很多学生会想到用“b”来表示，“但b 个能看出有这样的两份吗？”经教师提醒，有部分学生会想到用“2 个a”来表示，这样也就突破了低段学生只局限于具体数量的问题，出现了用代数符号表达的“2 倍”概念。】

三、拓展到几倍

练习一：第一行△△△。

画一画：第二行的△是第一行的3 倍。

师：如果第二行的△是第一行的5 倍、10 倍，又怎么画？

师：如果是1 倍呢？

练习二：

第一行△△△

第二行△△△△△△

师：第一行如果去掉一个△，第二行还是第一行的2 倍吗？那是几倍呢？为什么？

师：第一行如果去掉两个△，第二行是第一行的几倍呢？

练习三：

第一行△△△

第二行△△△△△△

师：如果以第二行为一份，第一行是第二行的几倍呢？

（画一画、说一说）

生：半倍。

生：0.5 倍。

师：这几位同学说得都对，这个我们以后会学到。

小结：如果以第一行的个数为一份，第二行有这样的几份，我们就说第二行的个数是第一行的几倍。

【设计意图：1.在这个环节有两个“变”：一是标准量不变，比较量变化（即两个量之间成正比例关系）。由于对“2 倍”有较为深刻的认识，所以对其他倍数，学生基本没有问题。在此基础上，引导学生认识较难理解的“1倍”，由于前期铺垫充分，学生的理解也水到渠成。二是比较量不变，标准量变化（即两个量之间成反比例关系）。“第一行如果去掉一个△，第二行还是第一行的2 倍吗？那是几倍呢？为什么？”“第一行如果去掉两个△，第二行是第一行的几倍呢？”让学生感受到比较标准的重要性，潜移默化地渗透反比例关系。在两个变中寻不变，基于丰富的体验，建立好“几倍”的结构。2.第一行3 个△，第二行6 个△。如果以第二行为一份，第一行是第二行的几倍呢？让学生打破刚刚形成的商大于或等于1 的几倍模型，渗透也有可能是不到1 倍的情况，为高段进一步学习分率（分数倍）做好铺垫。】

四、变式练习

第一题：

（ ）看作1 份，（ ）有这样的（ ）份，（ ）是（ ）的（ ）倍。

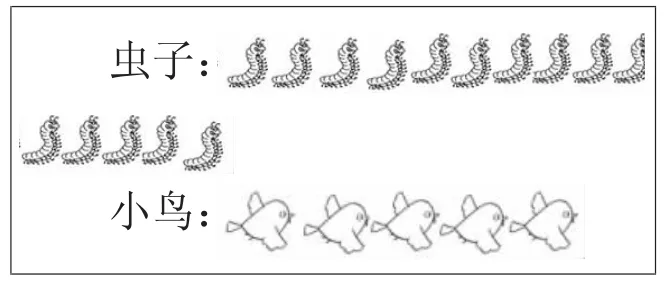
（ ）看作1 份，（ ）有这样的（ ）份，（ ）是（ ）的（ ）倍。

空白部分的大小是阴影部分的（ ）倍，整个长条的大小是阴影部分的（ ）倍。

第三题：○○●●○●○○

○○○○●○○○

○的个数是●的（ ）倍。

【设计意图：课的最后阶段，进一步通过变式检测和提升学生对倍的认识。分三个层次处理：第一题中的两个量虽然仍上下分开摆放，但需要学生自己辨识谁是标准量，谁是比较量。第二题是融成一行，探讨总体和部分之间的倍比关系。第三题是打乱了图形的排列，需要学生自己概括出两个量的关系。至第三题，学生完全摆脱了刻板的倍的图示，建立了抽象的倍的图式。】

类似于《倍的认识》这样的概念起始课，学生数学认知的发生是本质性的跃升。在这样的课中，学生对概念的理解程度，将深刻影响到后期学生解决问题、创造新知的水平。本节课设计的创新之处在于：一、学生在学习中，不断经历“破”与“立”的过程，层层剥离概念的非本质属性，建立新的数量关系模型。二、处处为学生的后续学习做铺垫。基于“倍”的概念，自然地联系到字母符号意识的渗透、标准量的变化、分数（小数）倍的建立、正反比例的涉及等等。“前有基础，中有突破，后有发展”是新思维数学的一贯理念，我们一线教师完全可以利用这样的理念，创造性地组织和改编学习材料，边破边立，融通教学，让概念教学更加扎实有效，真正促进学生数学思维的发展！