别让粗心成为借口

魏兰

【摘    要】在初中生学习数学的过程中，出现错误是不可避免的。因此，对错误的分析尤为重要，不能将每次的错误都归结为学生的粗心。其实错误也是从另一个角度揭示了学生学习中的思维缺陷。

【关键词】粗心;初中数学;错误浅析

中图分类号：G633.6       文献标识码：A      文章编号：1006-7485（2021）18-0187-02

Don't Let Carelessness Be an Excuse

——Analysis of Intuitive Errors in Junior Middle School Mathematics

（The Affiliated School of Yong'an No.1 Middle School，China） WEI Lan

【Abstract】In the process of junior high school students learning mathematics， mistakes are inevitable. Therefore， the analysis of errors is particularly important， and each error cannot be attributed to student carelessness. In fact， the error also reveals the thinking defects in students' learning from another angle.

【Keywords】Carelessness; Junior high school mathematics; Error analysis

一、對数学概念理解的肤浅性

由于学生在学习数学的过程中，对一些数学概念或数学原理没有深刻的理解，仅仅停留在表面概括上，无法把握事物的本质。因此学生在分析和解决数学问题时，往往只善于处理一些直观的或熟悉的数学问题，而对那些间接使用定理的数学问题，往往不能抓住其本质。

例题一：6a-a=6

对于刚从小学升上初中的学生来说，减去即等于消失，所以这样的错误并不少见，他们没有意识到6a是6个a，而只是简单地让字母a去除。同时，6a减a也涉及合并同类项的概念，正是由具有抽象性的字母计算来代替具体数字的一个重要概念。初中学生正处于经验型思维到逻辑型思维转换的过程，无法将抽象的概念运用于实际的题目中，往往做题时还是依赖自己的直观感知。甚至到了初三，这样的问题还会出现，个别学生会犯这样的错误，6[2]-6=[2]。

二、仅凭直观，粗浅判断

在解决数学问题时，经常会产生一些直觉是正常的，有时还是很可贵的，但是数学是一门严谨的科学，产生直觉后还要周密地思考、严谨地推理、精密地计算，否则以眼睛的直觉代替理性的思维就很可能会出现错误。

例题二：如图，在等腰直角△ABC中，∠ACB=90°， D为△ABC内一点，将线段CD绕点C逆时针旋转90°后得到CE，连接BE，若∠DAB=10°，则∠ABE是 A.75°B. 78° C. 80° D. 90°

因为其中说明了是旋转线段CD，应该是得到△BEC全等于△ADC，从而得到∠EBC=∠DAC=40°，可是学生只是根据看到图形，经过最简单的直观判断，选D的人居多。天文学家开普勒曾经说过：“当知识通过感官被直接提供给心灵时，是模糊、混乱和矛盾的，从而也就不可靠的。”教师要时刻教育学生确定事物的本质，不能只靠感觉，应该多一些理性的思考。

三、受思维定式的影响

学生受先前形成的知识经验、习惯的影响，容易形成认知的固定倾向，从而影响后来的分析判断，形成思维定式。在环境不变的条件下，定式会使人能够应用已掌握的方法，迅速解决问题，但是如果环境改变，也会影响人们的创造性。

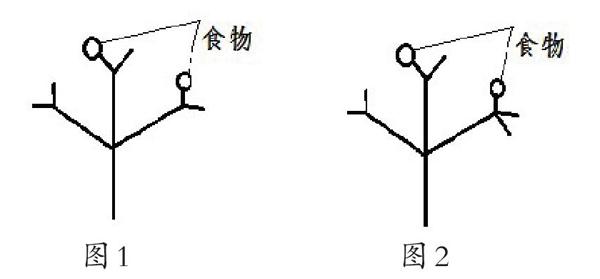
例题三：一只蚂蚁在如图所示的树枝上寻觅食物，假定蚂蚁在每个岔路口都会随机选择一条路径，那么它获得食物的概率是多少？

图1                               图2

图1和图2看上去图形非常类似，只不过图1有六个树枝，而图2有七个树枝。但是他们的概率却完全不一样。图1找到食物的概率是 [16+16=13]，而图2找到食物的概率是 [16+19=518]。学生通常用求图1的概率方法来做第二幅图的题目，却得出了[27]错误答案。没有意识到图1中每个树枝是等可能性的，而图2却不是。学生常常寻求表面上相似的东西，而忽略结构上、本质上的差异，最终导致理解错误。因此作为教师要引导学生在学习时，首先应该明白对一个问题不要急于按原先的套路求解，应该从模仿的路子跳出来，避免按部就班，而要先仔细地观察，学贵存疑，小疑则小进，大疑则大进，这才有可能让学生针对性地解决问题。

四、知识的负迁移

知识的负迁移是学生形成思维障碍的重要原因，面对一个新的数学问题，学生首先是联想与之形似或意似、且熟悉的问题，然后迁移解决问题的方法，将当前的问题与头脑中已有的知识经验之间建立起某种联系。这种以类比、联想为基础的思维活动，如果伴随着突破或者创新，那么就是课改所倡导的创新思维能力。如果只是一味地机械照搬，那么思维会呈现呆板，产生错误。如学习了有理数加法法则对乘法法则的学习会产生负迁移，学习同底数幂的乘法对幂的乘方产生负迁移。

五、分析问题不够全面

由于初中学生的年龄小，知识面较为狭窄，逻辑思维能力较为薄弱，分析问题时通常不够全面细致，而且通常在潜意识中容易出现臆断，造成解题过程中常常出现顾此失彼的现象。在学生进入初中高年级以后，数学知识点的面加宽、难度明显增大，而且有些问题已带有开放性的特征，如果学生一味依靠模仿与死记硬背的学习方法就难以奏效。表现在数学习题的解题中，就是缺少开放性思维方法，思路较为狭窄，往往就是顾此失彼，或者是解答过程简单化。

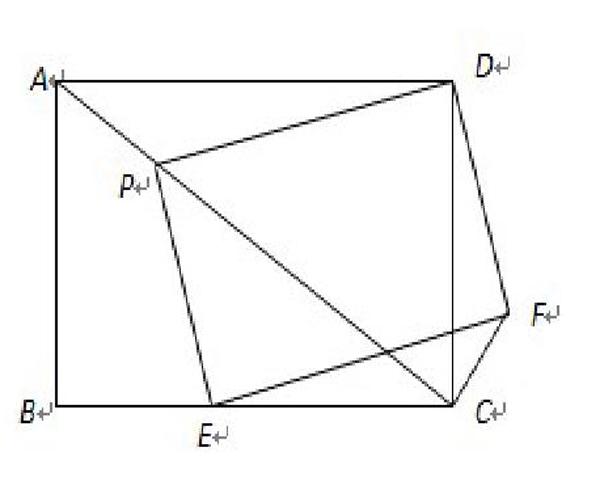
例题四：（17年福建）如图，矩形[ABCD]中，[AB=6，AD=8] [P，E]分别是线段AC、BC上的点，且四边形[PEFD]为矩形。

（Ⅰ）若[△PCD]是等腰三角形时，求[AP]的长;

[△PCD]是等腰三角形有三种情况[PC]=[PD]，[CP]=[CD]，[DP]=[DC]但是很多学生会被原题中给出的图形固定住思维，负略了P、E是可以动的，只考虑了DP=DC。

数学是一门具有高度抽象性和精密逻辑性的科学，思维的严密性是学好数学的关键之一。教师在授课过程中应该有意识地强调和培养学生思维的嚴密性，不要受现有图形和既定做法的影响。

六、将图形当成已知条件

将图形中出现的貌似的形状当成条件来解答，这在初中，尤其低年级学生群体中更是屡见不鲜。由于年龄段的特征，初中学生的智力还处于较为低级的阶段，对新生事物的认识、理解能力较差，而直观感知的能力却较强，他们常常会将图形中出现的类似等边三角形、直角三角形的图形当成已知条件来应用，教师应该及时提醒、纠正，引导学生由形象思维向抽象思维过渡。

例题五：已知：AB是⊙O的直径，AB=4，∠ABC=30°，D是BC中点且BD=4[3]，过点D作DE⊥AC。求证：DE与⊙O相切。

这道题学生做辅助线通常是连接AD，然后说明因为AB为直径，所以∠ADB=90°，但是实际上题目没有任何语句说明点D在圆上，这个结论是需要证明的。但是学生就是将图中看到的当成了已知条件，想当然地认为，点D已经在圆上了，忽略了对它的证明过程。

上述这些错误在学生的数学学习过程中并不少见，学生经常仅靠直观判断犯想当然的错误，当代科学家波普尔认为：“错误中往往孕育着比正确更丰富的发现和创造因素。”因此教师在教学过程中应不断地分析教材、研究学生，将那些容易出错的问题作为范例，认真上好错例分析课，直击要害，让学生体验错误，探究症结所在。而且应力争在课堂上给学生的不是一道题目的正确答案，而是一种思维方法，让学生发现错误的所在以及错误发生的原因，从中吸取教训，举一反三。在辨析错因、启发纠错的过程中，培养学生思维的严密性、广阔性、深刻性和创造性，让学生在错误中寻求正确的方向，反思错误的原因。然后对症下药，形成正确合理的认识，找到知识的薄弱环节并尽快弥补，力求在以后的解题中少出现错误或不出错，这也是学生反思成长的过程。

教师应该尽量在教学过程中培养学生的科学理性思维。初中学生的理性思维发展是靠数学来完成的。特别是学生的思维正处于从直观归纳向逻辑抽象思维转变的阶段。后续的高中数学学习对思维严谨性、逻辑性的要求更高，而且数学的理性思维方式远远超过了数学试题的本身，广泛应用于自然科学甚至人文科学和社会科学中，也对学生今后生活长期发挥积极的作用。所以不能只靠眼睛看到的表面现象来直观判断事物的属性，应该学会更深入理智地思考问题的本质，这才是学习数学带给学生真正的意义。

参考文献：

[1]王开珍. 初中数学解题错误浅析[J].宿州教育学院学报， 2002（02）.

（责编  侯  芳）