威布尔分布模型在巨龙竹林直径与年龄分布特征估测中的应用1)
2021-07-30郭强刘蔚漪辉朝茂官凤英邹学明
郭强 刘蔚漪 辉朝茂 官凤英 邹学明
(国际竹藤中心,北京,100102) (西南林业大学) (国际竹藤中心) (沧源县林业和草原局)
林分直径结构反映了林木个体随直径变化的分布状况,与林木的生长发育、生产力、生物量和林分的生态稳定性等密切相关,是重要且关键的生长特征因子和参数推导因子[1]。利用相关分布模型,如正态(Normal)分布、威布尔(Weibull)分布、逻辑斯蒂(Logistic)分布等,可以有效地表征林木直径分布规律,其中威布尔分布模型因其灵活性大、适应性强、参数易于求解等优势而被广泛用于林木直径分布拟合和预估[2-4],如蒙古栎(Quercusmongolica)、油松(Pinustabulaeformis)、杉木(Cunninghamialanceolata)等[5-7]。通常林木直径威布尔分布模型,主要指一元3参数威布尔分布模型,其位置参数(a)、尺度参数(b)、形状参数(c)与林木直径分布特征密切相关(当a=0时,即为2参数分布)。但综合看,分析直径与其它结构因子的二元威布尔分布模型比一元威布尔分布模型能更全面地反映林木直径分布的实际情况。为此,一些学者对林木直径与其它因子的二元威布尔分布模型进行了探索[8],在一定程度上为二元威布尔分布模型的理论研究和林业应用提供了参考[9];但其总体上还不成熟,相关研究成果也较少,还需进一步研究和完善。
巨龙竹(Dendrocalamussinicus)为禾本科竹亚科牡竹属特大型合轴丛生竹种,是中国西南地区特有珍惜竹种,同时也是迄今发现径级最大的竹种,有“世界竹王”之美誉[10]。但是长期以来,由于巨龙竹形态巨大、分布偏远,且分布山区地形与气候复杂等原因,对其相关研究较少,且较为局限,对其的保护和研究具有一定的紧迫性[11-12]。由于广泛适用于一般林木树种的威布尔分布模型,对这类特大型丛生竹种的适用性还不确定,这一珍稀竹种的直径分布规律还不清晰,为此,本研究以滇西南连续分布的整个巨龙竹林分为试验对象,于2019年12月份,筛选得到健康且非林缘处生长的巨龙竹共计93丛,对其竹高达到主林层及以上的2090株巨龙竹进行直径和年龄检尺统计;采用一元3参数威布尔概率密度函数模型、二元威布尔生存函数模型、导出的2种改进二元威布尔概率密度函数模型,分析滇西南巨龙竹林直径与年龄分布特征。旨在为巨龙竹林业工作开展和林用二元威布尔分布模型研建提供参考。
1 研究区概况
研究区位于云南省临沧市沧源佤族自治县(98°52′~99°43′E、23°4′~23°40′N),属亚热带季风气候类型,干湿季分明,一般夏秋季为雨季、春冬季为旱季;年平均气温21 ℃,年积温约7 500 ℃,年降水量约2 100 mm,月均空气相对湿度约80%;土壤类型主要为红壤、赤红壤、砖红壤等;林下分布植被主要为小叶肉实树(Sarcospermagriffithii)、光叶火筒树(Leeaglabra)、猪肚木(Canthiumhorridum)、多羽凤尾蕨(Pterisdecrescens)、破坏草(Ageratinaadenophora)等。
2 研究方法
2.1 样地选择与数据调查
以研究区班洪乡处连续分布的整个巨龙竹林分为试验对象(见表1)。2019年12月份,筛选得到健康且非林缘处生长的巨龙竹共计93丛,对其竹高达到主林层及以上的2 090株巨龙竹进行直径和年龄检尺(见表2)。

表1 研究样地基本概况
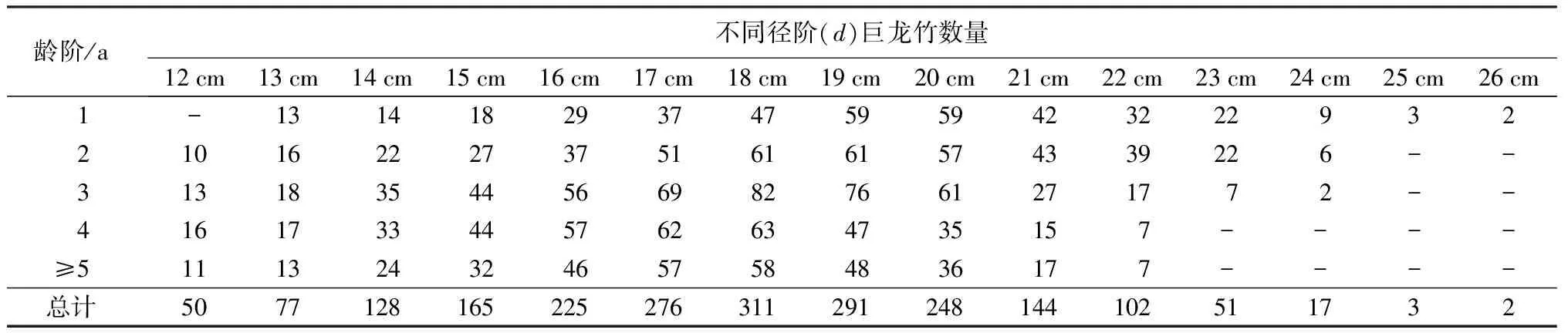
表2 研究样地的巨龙竹直径与年龄分布统计
2.2 分布模型选择
2.2.1 一元3参数威布尔概率密度函数模型
一元3参数威布尔概率密度函数分布模型,即式(1):
f(D)=[(D-a)/b]c·[c/(D-a)]·exp{-[(D-
a)/b]c}=(c/b)·[(D-a)/b]c-1·exp{-
[(D-a)/b]c}。
(1)
式中:a为位置参数,与林木直径分布最小值有关;b为尺度参数,与林木直径分布范围有关;c为形状参数,与林木直径分布形状有关。
2.2.2 二元威布尔生存函数模型
二元威布尔生存函数分布模型[9],即式(2):
N(D>d,T>t)=n·P(D>d,T>t)=n·exp{-[(d-
a1)/b1]c1+(t/b2)c2}。
(2)
式中:a1为位置参数,与林木直径分布最小值有关;b1、b2为尺度参数,分别与林木直径和年龄分布范围有关;c1、c2为形状参数,分别与林木直径和年龄分布形状有关;n为数量参数,与林木分布总数量有关;P(D>d,T>t)为林木的生存概率。
2.2.3 改进的二元威布尔概率密度函数模型
研究表明[8,13-14],一元3参数威布尔分布模型的3个参数(a、b、c)与部分林分结构因子具有多元线性或指数等回归关系。因此,假设其分布模型的3个参数(a、b、c)和林木直径、年龄分别具多元线性及指数回归关系,则有:
c1=g1+g2·T+g3·D、b1=g4+g5·T+g6·D、a1=
g7+g8·T+g9·D;
将相关回归式对应代入式(1)后,导出2种改进的二元威布尔概率密度函数分布模型,即式(3)、式(4):
f1(T,D)=g10·[(g1+g2·T+g3·D)/(g4+g5·T+
g6·D)]·{[D-(g7+g8·T+g9·D)]/(g4+g5·T+g6·D)}(g1+g2·T+g3·D-1)·exp{-[D-
(g7+g8·T+g9·D)]/(g4+g5·T+g6·
D)}(g1+g2·T+g3·D);
(3)

(4)
式中:g1、…、g10为改进的二元威布尔分布模型Ⅰ,即式(3)的参数;q1、…、q10为改进的二元威布尔分布模型Ⅱ,即式(4)的参数。
利用Office Excel 2007和SPSS 19.0进行数据整理和分析。
3 结果与分析
3.1 巨龙竹直径的一元威布尔概率密度函数模型拟合及求解
3.1.1 巨龙竹直径分布服从威布尔分布假设检验
概率散点图可检验样本数据是否服从某种理论分布,即当符合既定理论分布时,各数据点在概率散点图中近似呈一条直线地分布于右斜对角线位置,而在无趋势概率散点图中则呈离散分布。对现实巨龙竹林分直径分布进行威布尔分布检验(见图1、图2),由图1、图2可见,概率散点图中的各数据点近乎一条直线地分布于“Y=X”线处,而无趋势概率散点图中的各数据点则呈离散状分布于“Y=0”线的上下侧。因此,可以认为现实巨龙竹林分直径分布服从威布尔分布。

图1 巨龙竹直径分布概率散点图

图2 巨龙竹直径分布无趋势概率散点图
同时,利用柯尔莫可洛夫-斯米洛夫检验(K-S)检验法对巨龙竹直径分布进行假设检验。首先假设其直径分布服从威布尔分布,计算其统计量Dn=sup[Fn(x)-F(x)]=0.010 959,经查表(0.05水平)得其临界值D=0.029 749,通过检验可知Dn 3.1.2一元3参数威布尔概率密度函数模型求解与评价 应用牛顿迭代法求解一元3参数威布尔分布模型的3个参数值(a、b、c)。根据一元威布尔分布模型参数值与其分布形状的关系,并结合巨龙竹直径分布的散点图,分别选取其初始值为5.3、12.0、2.5。经过12次迭代后稳定(表3为最后5次迭代结果),并得最优解:a=5.330 583、b=13.409 918、c=5.154 559。因此,可以确定,巨龙竹直径分布的一元3参数威布尔概率密度函数最优预估模型为: 表3 最后5次迭代过程 f(D)=[(D-5.330 583)/13.409 918]5.154 559· [5.154 559/(D-5.330 583)]·exp[-(D- 5.330 583)/13.409 918]5.154 559, R2=0.993 436。 根据巨龙竹直径分布的实际观测和分布模型拟合结果(见表3、图3)分析可知,巨龙竹直径一元3参数威布尔分布模型的拟合效果优良,其拟合的决定系数R2=0.993 436、平均绝对误差值ε=0.003 183。巨龙竹林分直径分布呈单峰状,主要分布于16~20 cm,其它径阶的巨龙竹数量则相对较少;其直径分布的偏度值和峰度值分别为0.282 982、-1.378 235。 图3 巨龙竹直径分布观测数据与威布尔分布拟合 3.2.1 二元威布尔生存函数模型求解 3.2.2 二元威布尔生存函数模型评价 巨龙竹直径与年龄的二元威布尔生存函数模型可适用于其林分直径与年龄分布规律研究,其拟合的决定系数R2=0.997 341、平均绝对误差值ε=64.013 527。利用二元威布尔生存函数预估模型对巨龙竹的生存株数进行预测,并与实际观测值对比(见表4)。由表4可知,巨龙竹生存株数随直径分布的下降幅度在不同年龄特征的变化趋势基本类似,即慢-快-慢的降幅变化,且包含的年龄结构信息量越大,其降幅程度也越大,这间接地反映出巨龙竹林直径分布呈单峰状分布的特点。同时,将生存株数的分布模型预估值分别除以n(即2 145.405 447),可相应地得到巨龙竹林直径与年龄分布的生存概率预测值。 表4 巨龙竹生存干数的实际观测值与理论分布值 3.3.1 改进二元威布尔概率密度函数模型求解 应用牛顿迭代法求解2种改进的巨龙竹直径与年龄二元威布尔概率密度函数模型的相关参数,并将其参数估计值对应代入其分布函数模型表达式式(3)、式(4)式后,则有: 图4和图5反映了2种改进的巨龙竹直径与年龄二元威布尔概率密度函数模型的拟合特征。由图4、图5可见,其分布形状在直径和分布概率的投影上,均呈一元威布尔分布状,各年龄竹的直径分布较为稳定,但彼此仍略微差异,其总体上表现为新生竹比老竹的直径有逐渐增大的趋势,这与林分实际情况相吻合。可见,考虑竹年龄特征的二元威布尔分布模型,在反映巨龙竹林分直径分布特征方面比一元威布尔分布模型更为客观、全面。 图5 巨龙竹直径与年龄的二元威布尔分布模型Ⅱ 3.3.2 2种改进二元威布尔概率密度函数模型评价 综合2种改进的二元威布尔概率密度函数模型拟合巨龙竹林直径与年龄分布结果,并与现实林分实际观测值对比(见表5),由表5可见,2种改进的二元威布尔分布模型对巨龙竹林直径与年龄分布的拟合效果良好,其拟合的决定系数分别为0.919 323、0.906 260,平均绝对误差值分别为0.000 072、0.001 325,可满足基本的精度要求。根据现实林分巨龙竹总干数乘以表5中对应径阶与龄阶的理论分布概率值,可得到其林分直径和年龄分布的估测预期值。 表5 巨龙竹直径与年龄的实测概率值和理论概率值 葛宏立等[9]在对浙江省毛竹(Phyllostachysheterocycla)直径与年龄二元威布尔分布模型研究中,提出了一种二元威布尔生存函数模型,并认为其研究方法在理论上可应用于毛竹林分。本研究中,利用二元威布尔生存函数模型可较好地反映巨龙竹林分直径与年龄分布特征,说明这类分布模型,不仅可以应用于林分,还可适用于巨龙竹这样的特大型丛生竹种。但是,该类分布模型的拟合结果具有累积式分布特征,难以快速且方便地反映具体径阶与龄阶的林木直径与年龄分布状况,而二元威布尔概率密度函数模型在这方面则具有一定的优势。本研究通过一元3参数威布尔分布模型参数(a、b、c)对林木直径与年龄进行多元线性、指数回归,导出了2种改进二元威布尔概率密度函数模型,并均具有良好的拟合效果,可满足基本的精度要求,其中由多元线性回归导出的改进二元威布尔分布模型,与周国模等[8]研究结果相似。 本研究中,在利用迭代法求解2类3种二元威布尔分布模型的多个模型参数时,均存在参数初始值选取困难等难题,这常常使得模型参数值计算工作量大、拟合效果不佳。因此,如何巧妙且恰当地选取二元分布模型参数初始值,以便于高效且准确地得到其模型参数最优解,还需进一步研究。 本研究中,二元威布尔生存函数模型在对巨龙竹直径与年龄分布拟合时,尽管难以直观地反映各个径阶与龄阶的竹株具体分布特征,但其拟合精度较高,且模型参数值的生态学意义明确。本研究中,对于尝试改进的2种二元威布尔概率密度函数模型,尽管较为真实且方便地反映了巨龙竹林直径与年龄分布情况,但其模型多个参数值的生态学意义还不明确,甚至其分布模型本身也有待于从数学理论层面做进一步考证。同时,本研究未能考量巨龙竹“丛生”这一特性,如何在巨龙竹或其它丛生竹种的二元或多元威布尔分布模型研究中引入“竹丛”这一特征因素进行分析,还需深入研究。 此外,本研究通过最小二乘的牛顿迭代法求解一元3参数威布尔概率密度函数模型拟合巨龙竹直径分布概率、二元Weibull生存函数模型拟合巨龙竹直径与年龄生存株数、2种改进二元威布尔概率密度函数模型拟合巨龙竹直径与年龄分布概率的参数最优解,而针对不同的分布模型类型、参数估计方法、变量含义等会对其模型拟合效果产生怎样的变化,仍需进一步探讨。 利用一元3参数威布尔分布模型可以较好地描述巨龙竹林直径分布特征;而利用巨龙竹直径与年龄的二元威布尔生存函数模型和2种改进二元威布尔概率密度函数模型,则可以更加真实地反映考虑年龄特征的巨龙竹林直径分布规律。综合各类威布尔分布模型拟合特征认为,巨龙竹林直径分布呈单峰状,主要分布于16~20 cm,且具有新生竹比老竹直径逐渐增大的变化趋势。 本研究分别建立了巨龙竹林直径一元3参数威布尔概率密度函数最优预估模型、直径与年龄的二元威布尔生存函数最优预估模型、直径与年龄的2种改进二元威布尔概率密度函数最优预估模型,并在此基础上得到了巨龙竹林直径与年龄的生存数量(概率)和分布概率的理论估测数表,可满足基本的精度要求。相关研究方法和结果可为今后巨龙竹林业工作开展和林用二元威布尔分布模型研建提供参考。

3.2 巨龙竹直径与年龄的二元威布尔生存函数模型求解与评价

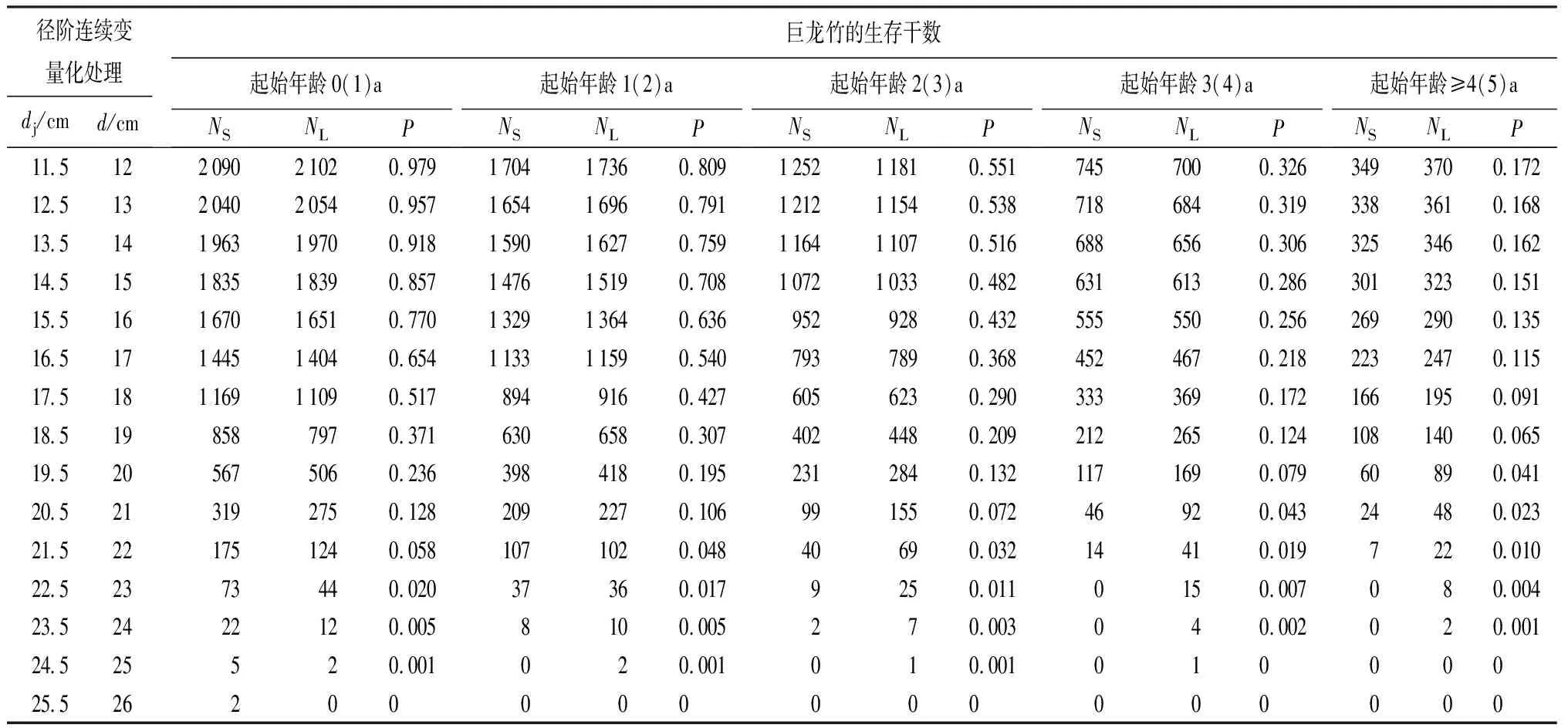
3.3 巨龙竹直径与年龄的二元威布尔概率密度函数模型求解与评价
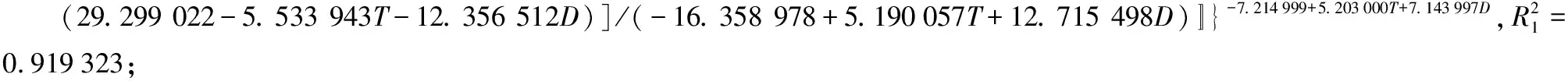

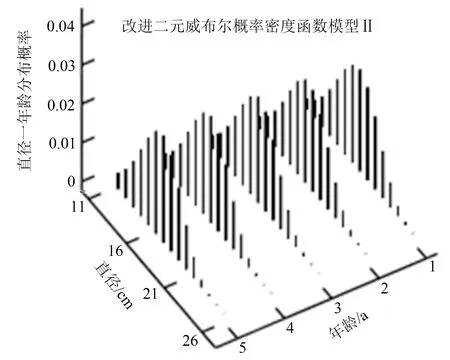

4 讨论
4.1 林木直径与年龄的二元威布尔分布模型及求解
4.2 林木直径与年龄的二元威布尔分布模型适用性评价
5 结论
