导弹箱式发射初始扰动仿真与试验研究
2021-07-30吴俊全王军辉
吴俊全,王军辉,杨 森
(西安航天动力技术研究所固体火箭发动机燃烧、热结构与内流场国防科技重点实验室,西安 710025)
0 引言
倾斜导轨发射是各种战术导弹在装箱状态下大量采用的一种发射方式[1]。导弹发射时,在动力装置作用下,导弹通过自身滑块与导轨配合约束,沿导轨滑行预定的距离后,导弹离轨。离轨时,导弹具有一定的离轨速度和运动姿态[2]。对于顺序离轨形式,由于在离轨过程中导弹存在半约束状态,其运动姿态会发生变化。导弹离轨速度主要受发射倾角、发射过载、以及导弹在轨有效滑行距离的影响。导弹出箱离轨的运动姿态受质心位置、导轨和滑块实际配合间隙、配合面的平面度、滑块相对质心位置、动力装置推力横移和偏斜等多种因素影响。因此会出现导弹俯仰和偏航方向上姿态的变化,对导弹的精度和命中概率有较大影响。
目前关于导弹发射离轨的相关技术文献中,多以导弹离轨安全性分析为主,陈全龙等通过有限元仿真分析模型,对机载导弹离轨过程中导弹的离轨时间、离轨姿态、导弹滑块与滑轨接触力等进行了离轨安全性研究[3]。程运江等对前后滑块同时离轨的倾斜发射方式进行了发射动力学仿真分析,表明增大初始射角可减小发射初始扰动,且质心偏差对导弹姿态变化较为敏感[4]。
文中以某型号导弹的出箱离轨过程为研究对象,通过适当的简化,建立相应运动分析的数学模型[5],得到出箱过程中导弹的运动方程。为导弹出箱离轨扰动分析提供理论支撑,为导弹总体参数提供参考。
1 导弹与导轨配合形式
某型导弹采用前后两组T型滑块吊挂在发射箱内导轨下方,滑块与导轨配合形式如图1所示,导轨与滑块之间根据需要设计相应的配合间隙。
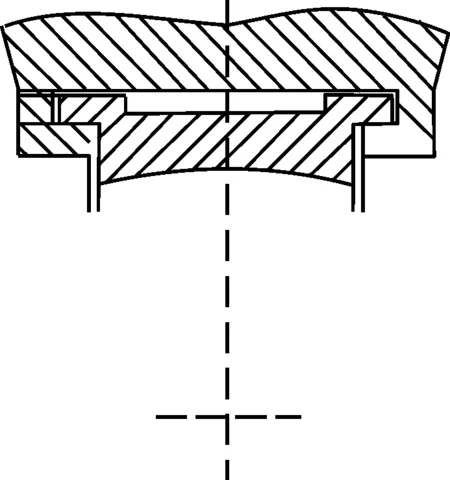
图1 滑块与导轨截面配合形式
弹体滑块与导轨布局图如图2所示。前、后滑块分别位于质心两侧。其中L1为前滑块距导轨前端距离;L2为前滑块距弹体质心距离;L3为后滑块距弹体质心距离;L4为后滑块距弹尾距离。发射时滑块在导轨槽内沿导轨滑行,其运动过程可分为3个阶段:
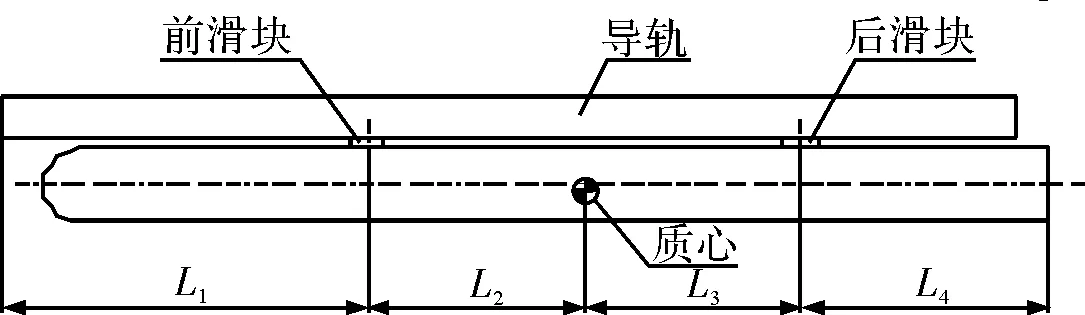
图2 弹上滑块布局图
第一阶段,约束段,即弹体前后滑块在导轨上的滑行段,此时,导弹受两滑块约束。导弹滑行过程中可能出现两滑块均与导轨下表面接触;前滑块与导轨下表面接触、后滑块与导轨上表面接触(即低头);前滑块与导轨上表面接触、后滑块与导轨下表面接触(即抬头)3种情况,该阶段导弹滑行距离如图2中的L1。
第二阶段,半约束段,即前滑块已经滑离导轨,而后滑块仍在导轨上滑行运动。此时会出现弹体绕后滑块转动,该阶段导弹滑行距离如图2中的(L2+L3)。
第三阶段,无约束段,即前后滑块均滑离导轨,弹体不受导轨约束。弹尾离开导轨即认为导弹完全出箱,该阶段导弹滑行距离如图2中的L4。
由于在俯仰方向较偏航方向上姿态影响因素较多,以下仅对导弹俯仰姿态进行分析。
2 数学模型及仿真计算
2.1 数学模型
从计算分析的实际需要出发,对模型作以下简化:
1)导弹和发射箱是刚体;
2)导轨与滑块配合面为平直面;
3)摩擦力为平行于弹轴的常值;
4)导弹发射前导轨处于固定状态;
5)假设弹体质量为恒定值。
2.1.1 第一阶段
前滑块离轨前,弹体受力如图3所示。
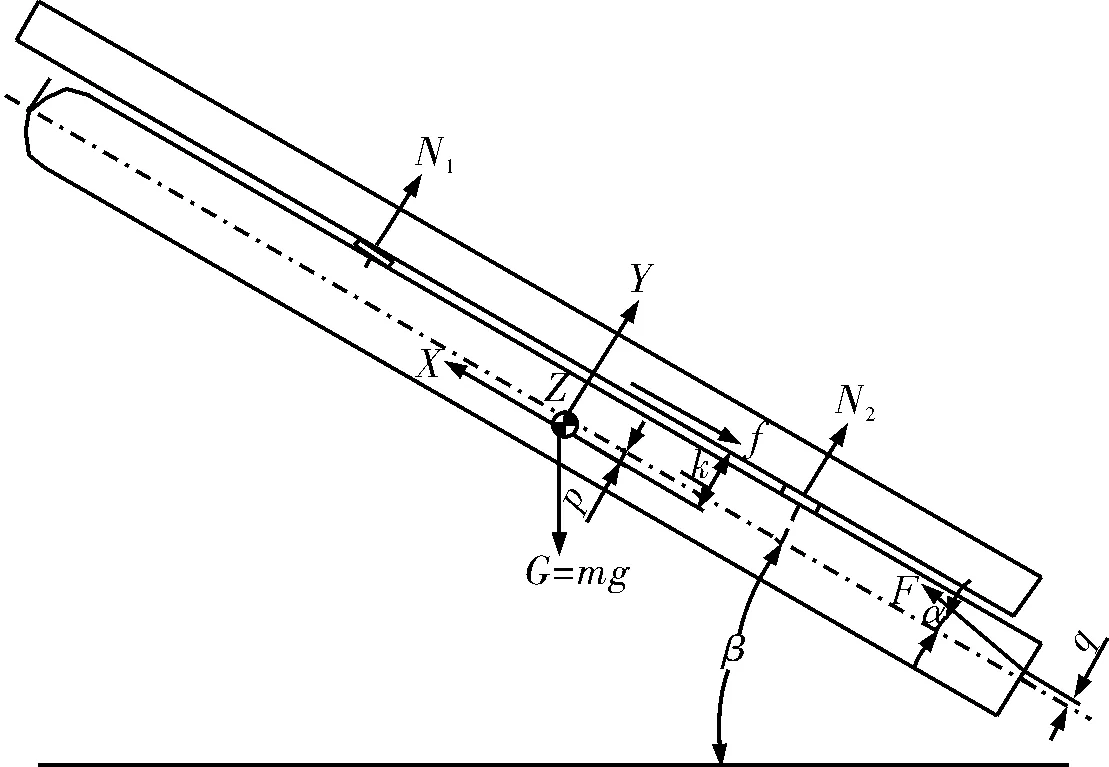
图3 导弹离轨过程受力分析
其中:f为导弹与导轨摩擦力;μ为摩擦系数;N1,N2为导弹前、后滑块所受的支反力;F为动力装置推力;α为动力装置推力偏斜角;β为导弹发射仰角;φ为导弹俯仰角;m为导弹的质量;JZ为弹体相对弹体坐标系Z轴的转动惯量;p为导弹质量偏心;q为动力装置推力横移;k为滑块与滑轨接触面距弹体质心距离。
根据图3受力分析可得:
(1)
(2)
(3)
式(3)中等式两侧为正,导弹出现抬头现象;等式两侧为负,导弹出现低头现象。常规状态下,该工况既不会出现导弹抬头现象,也不会出现低头现象。即导弹两滑块均与导轨下表面一直处于接触状态。
2.1.2 第二阶段
前滑块离轨后,后滑块离轨前,图3中N1=0。
根据受力分析可得:
(4)
(5)
(6)
式(6)中等式两侧为正,导弹出现抬头现象;等式两侧为负,导弹出现低头现象。常规状态下,该工况仅出现导弹低头现象。
2.1.3 第三阶段
后滑块离轨后,弹尾离开导轨前。图3中N1=N2=0。
根据受力分析可得:
(7)
(8)
(9)
式(9)中等式两侧为正,导弹出现抬头现象;等式两侧为负,导弹出现低头现象。常规状态下,该工况仅出现导弹低头和下沉现象。
2.2 仿真计算结果
通过PRO/E进行导轨与滑块配合设计,将最终状态导入ADAMS/View进行运动分析[6],输入各结构件材料、质量特性等参数,施加约束和边界条件。模型中动力装置推力以实测推力曲线作为输入条件,动力装置推力曲线如图4所示。前后滑块与弹体之间使用固定副连接;两滑块与导轨之间定义接触,可以沿弹体X轴方向运动,导轨采用固定副形式。
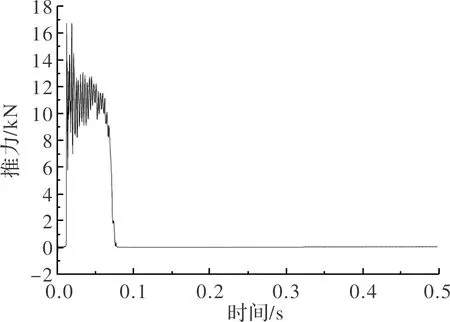
图4 动力装置推力曲线
根据动力学计算结果,在标准设计状态下,导弹离轨过程中俯仰角度、角速度随时间的曲线如图5和图6所示。
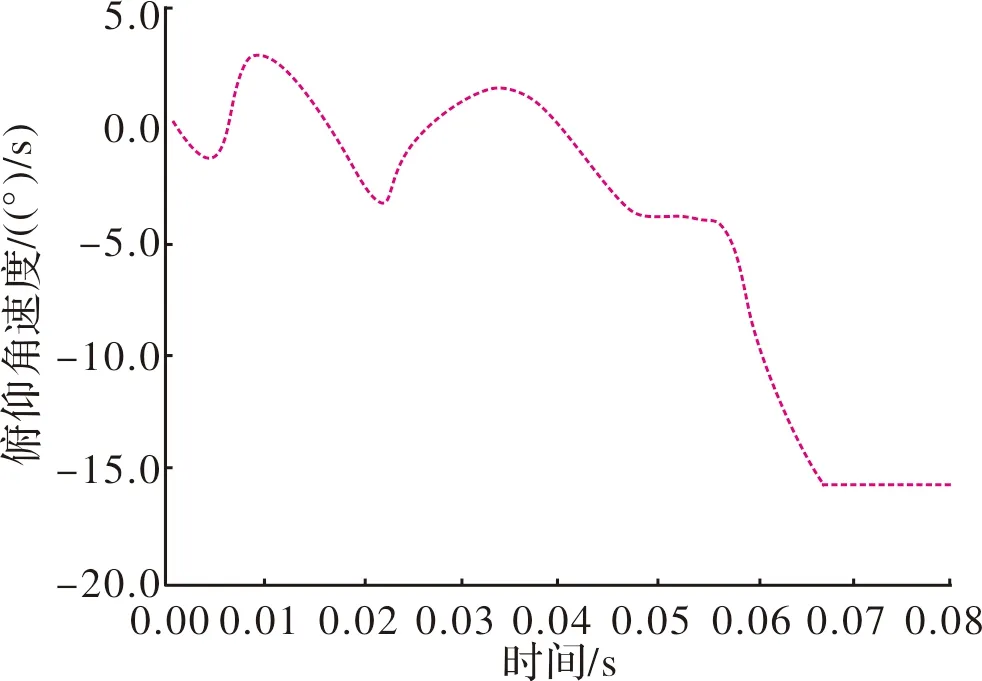
图5 标准设计状态下俯仰角速度与时间关系
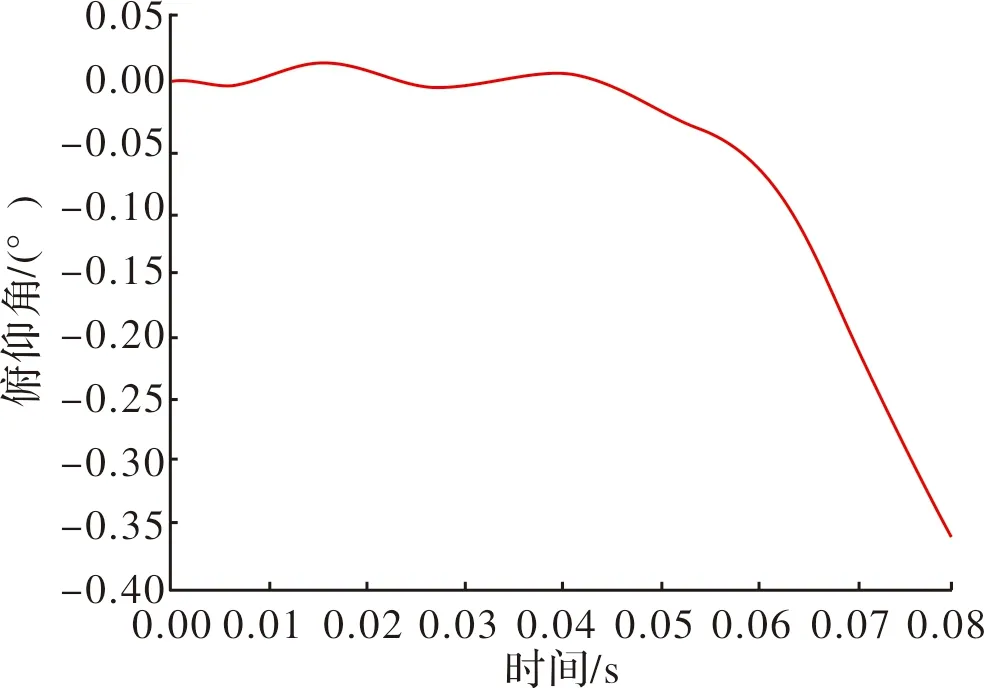
图6 标准状态下俯仰角度与时间关系
2.3 出箱姿态影响因素分析
根据发射箱导轨与滑块配合形式,对弹体出箱离轨姿势的主要影响因素有:导弹的转动惯量偏差δJZ、质量偏心p、导弹滑块与导轨的摩擦力即摩擦系数μ、动力装置的推力横移q1和偏斜q2。两种极限偏差如表1所示。

表1 两种极限偏差
将以上组合形式作为模型前处理的输入条件,其中质量特性通过弹体质量特性参数直接调整。通过动力装置对弹尾的不同作用点,实现动力装置的推力横移;通过增加Y向作用力与弹体轴线X向作用力的共同作用实现推力的偏斜模拟。
在表1所示的极限条件下,计算得导弹俯仰方向角度和角速度随时间曲线如图7和图8所示。
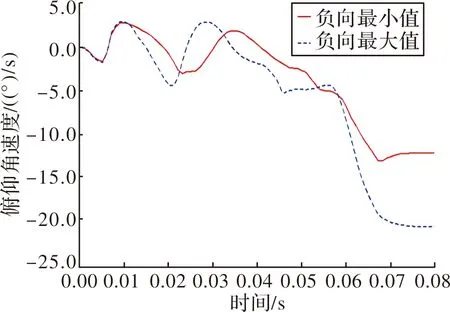
图7 极限条件下俯仰角速度与时间关系
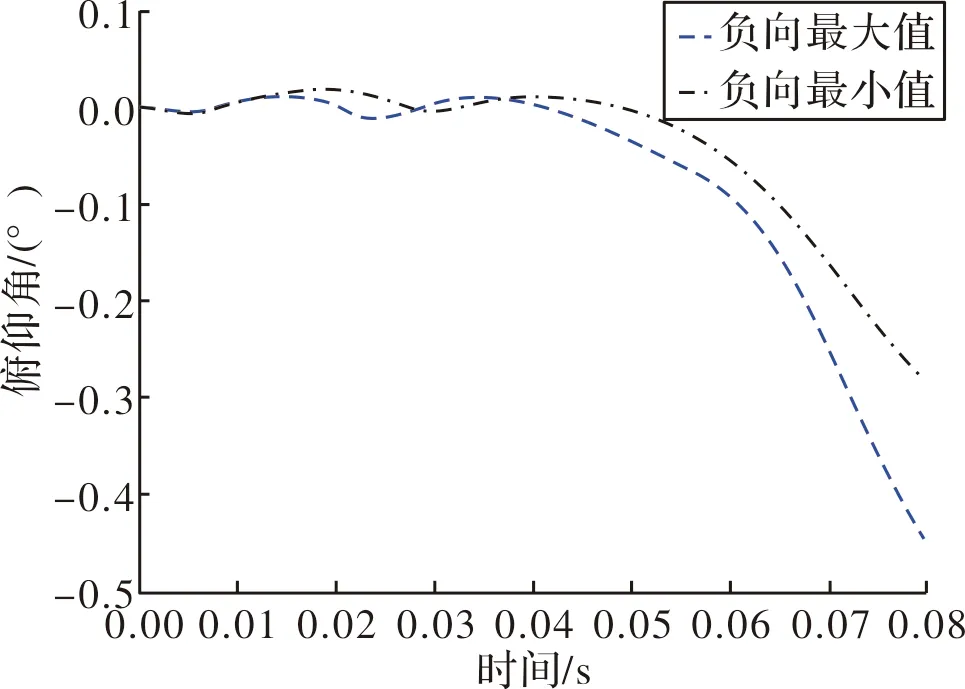
图8 极限条件下俯仰角度与时间关系
3 飞行试验结果
通过弹载记录装置对3发飞行试验产品中角速度传感器数据进行判读。每间隔5 ms进行一次导弹姿态采样,其结果如图9所示。在动力装置初始点火工作冲击作用下,弹体以及整个发射系统均发生振动,导致整个导弹在出箱过程中处于高频振动状态,而且采样较少,初始段不能真实反应导弹的俯仰姿态,动力装置稳定工作后,导弹俯仰姿态均收敛,且出箱离轨时刻,3发产品俯仰角速度较一致,均处于15°/s~25°/s之间。将角速度进行积分,得到俯仰角度与发射时间之间关系,如图10所示。根据试验数据,导弹完全出箱时刻约为70 ms,此时导弹俯仰角为-0.5°~-1.2°之间,即导弹低头角度最大为1.2°。
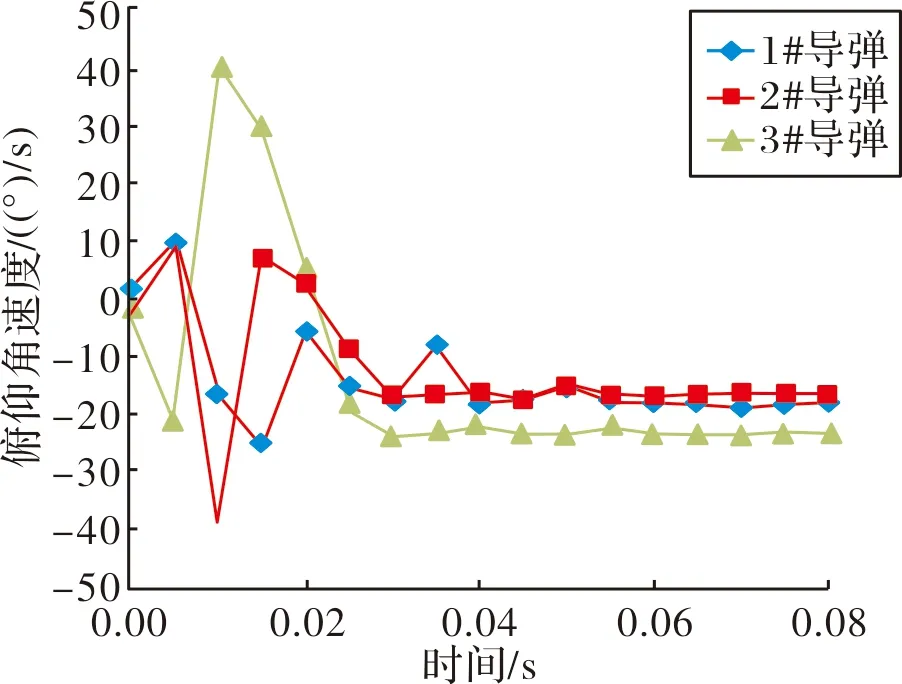
图9 飞行产品俯仰角速度-时间曲线
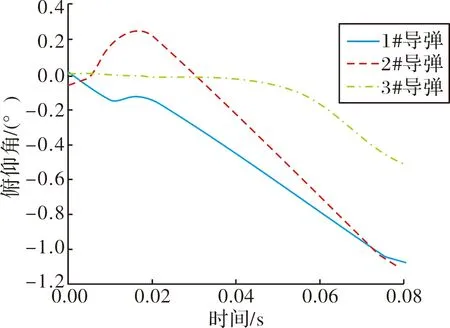
图10 飞行产品俯仰角-时间曲线
4 仿真与试验结果对比分析
将俯仰角速度的试验结果和仿真极限情况进行比较,其结果见图11。从图中可以看出,导弹实际飞行出箱过程中在俯仰方向的扰动较仿真结果振荡更为明显,出箱时刻一致性较好。
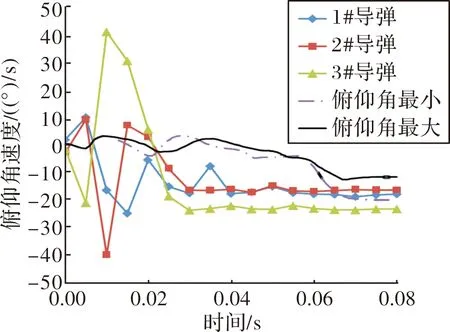
图11 俯仰角速度试验与计算比较情况
经分析,由于导弹与地面发射装置之间导致低头的所有配合间隙,均在导弹发射初期振动飞行过程中消除,因此,在导弹出箱前期,试验测得的数值较计算值偏大,后期一致性较好。
5 结论
ADAMS动力学仿真计算和飞行试验数据对比结果表明:
1)模型可以真实模拟导弹离轨出箱时导弹的运动姿态,仿真和飞行试验结果一致性较好。
2)导弹出箱时,影响导弹姿态的因素较多,姿态俯仰角速度范围较大,仿真结果为12.0°/s~20.5°/s,飞行试验结果为16.6°/s~23.4°/s。
3) 在动力装置初始点火工作冲击作用下,弹体以及整个发射系统均发生振动,导致整个导弹在出箱过程中处于高频振动状态,俯仰角度受整个发射系统影响较大。
