基于PNN某型弹载计算机故障诊断

唐 颜，徐天蒙，周 伟，王改堂，蔡睿洁

(西安现代控制技术研究所，西安 710065)

0 引言

弹载计算机作为弹上的控制中心，其硬件性能是决定武器系统运行状态的重要因素[1]，因此需要对其硬件性能进行充分鉴定。

目前的鉴定方式中，弹载计算机的检测状态通过总线接口以十六进制数据形式输出，形成对应文本文件[2]，测试人员对数据逐一分析判定是否存在异常。然而，文本文件中数据规模大，若要充分鉴定硬件性能，就面临着巨大的数据分析，采用现有的人工分析方式耗时长且容易出现疏漏。

神经网络可用来对数据进行故障分类，但目前基于神经网络的分类方式多以单一特征量作为故障提取依据；而弹载计算机的每帧检测数据含有多个故障特征量，因此传统的神经网络方式难以直接进行分类。

针对上述问题，提出一种基于概率神经网络PNN的弹载计算机故障诊断方法。该方法可将每个文件的存储数据由矩阵形式简化为向量，以此作为数据输入的特征向量；然后采用特定编码方案，对所有特征量进行映射，得到与之对应的唯一编码输出，形成故障编码集；同时采用PNN对编码集的输入输出进行模型训练，实现多故障特征量、大容量数据输入下的故障分类，仿真结果验证了该方法的可行性及有效性。

1 故障编码集建立

1.1 故障输入数据处理

检测结果中的数据帧由帧头、测试项1结果、测试项2结果、…、测试项n结果、校验和构成。对于每一数据帧而言，将其测试结果以A表示：

Ai=[Ai1,Ai2,Ai3,…,Ain]

(1)

式中：n为检测项数量；Ain为第i帧数据第n项检测结果，取值为0(正常)或1(异常)。总共m帧数据则构成一个故障输入矩阵A：

(2)

式中，每列数据为同一检测项的不同时刻的故障检测结果，若按测试类别进行分类，则矩阵A又可表示为：

A=[X1,X2,…,Xn]

(3)

其中：

Xi=[A1i,A2i,…,Ami]T,i=1,2,…,n

(4)

接下来求取向量Xi的模Mi：

(5)

若Mi不等于0，则代表向量Xi中存在非零值，即第i类测试项存在异常，将Mi置1(i=1,2，…，n)，按此方式，求出所有测试项对应的模Mi，构成新的向量：

B=[M1,M2,…,Mn]

(6)

由此，输入数据由m×n矩阵A转换为n维向量B，以此作为数据的特征向量，简化数据分析规模。

1.2 故障编码函数确定

若弹载计算机检测项数量为n，每个检测项包含正常和异常两种情况，则共有2n种结果，当所有检测项均正常时，弹载计算机才算是检测正常，剩下2n-1种测试情况均视为故障。

结合1.1节分析可知，由n项检测数据构成的故障输入矩阵A，可转换成n维向量B，作为检测数据的特征向量。为了将特征向量B映射至2n-1种故障结果组成的故障空间，需求取故障编码函数f，使每一种特征向量B的取值都与相应的故障结果r一一对应，三者之间满足关系式如下：

r=f(B)

(7)

由于向量B的组成元素为0或1，因此若将向量B中的元素组合视为二进制数据的高低位，则存在唯一的十进制数值与之相对应。

如表1所示，确定故障特征向量B以后，可采用二进制转十进制方式得到唯一数值，用来表示与之对应的故障输出结果r，实现故障输入到输出之间的映射。因此，故障编码函数f表达式为：

4.3 词汇密度与“个性风格词汇”之计算。词汇密度计算方中，实词是指名词、动词、形容词和副词四类。根据Biber(2000：62),计算公式是：词汇密度=实词数÷总词数×100%。Ure指出，词汇密度可以作为区别语体正式程度的一个指标，某文本的词汇密度越高，则该文本的语体越接近正式端；反之，若该文本词汇密度低，则可以说明，该文本越靠近非正式端，越接近自然口语。据Ure(1971：443-452)的研究，口语的词汇密度大概通常低于40%，而在书面语里，词汇密度通常要超过40%。

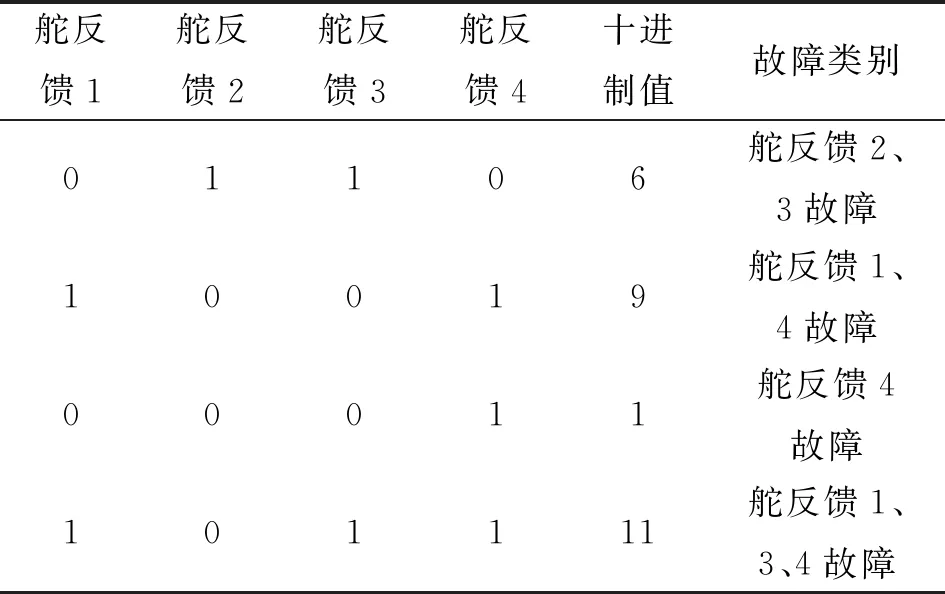
表1 故障编码用例

f=M1×2n-1+M2×2n-2+M3×2n-3+…+Mn-1×2+Mn

(8)

通过式(8)即可得到故障输入与故障输出种类的映射关系，进而形成弹载计算机故障输入输出数据集，再利用概率神经网络对上述样本进行模型训练，实现弹载计算机故障诊断。

2 基于PNN的故障诊断

2.1 PNN结构及分析

PNN是径向基网络的一个分支，由输入层、模式层、求和层、输出层构成，具体结构如图1[3]。

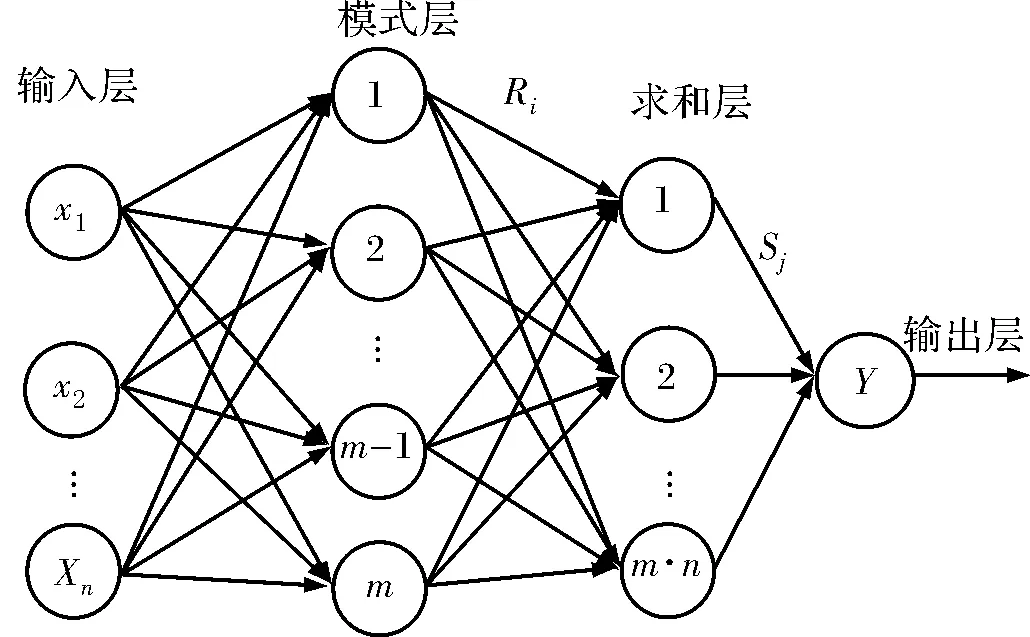
图1 PNN结构图

如图1所示，输入层由n个神经元构成，其个数为输入向量的维数，输入层计算输入向量与所有训练样本向量之间的距离。m个作为隐神经元构成模式层，该层采样高斯函数作为激活函数，计算测试样本与训练样本中的每一个样本的高斯函数的取值，计算公式为[4]：

(9)

式中：σi为平滑系数；Xi为训练样本；Z为待训练的输入样本。

求和层的神经元个数与总的类别数量一致，求取相同类别测试样本对应的模式层节点输出之和：

(10)

式中：j为样本种类，取值为1到m的整数；n为输入特征向量的维度；训练样本中故障类型为j的样本有tj个；i为故障类型j的样本排列数值[5]。

输出层输出求和层神经元中后验概率最大者：

Y=max(Sj)

(11)

2.2 基于PNN的故障诊断模型设计

I=[B1,B2,…,Bm]T

(12)

式中m为输入样本个数。

若检测项数量为n，则PNN故障模型输出向量为Y=[1,2,3,…,2n-1]T。整个故障诊断流程如图2所示。

图2 弹载计算机故障诊断流程

2.3 实验结果分析

现选取某型弹载计算机的环境试验测试数据为样本，对文中提出的测试方法进行检验，数据中检测项包含Flash检测结果、IO初始状态、舵反馈1 AD采集精度、舵反馈2 AD采集精度、舵反馈3 AD采集精度、舵反馈4 AD采集精度共6项内容。为了保证测试的准确性，选取常温、低温、高温、冲击振动、低温贮存、高温贮存等多个环境条件下的试验数据作为训练样本，且覆盖所有故障类型，现将上述条件各选取50个样本，总共300组数据，将其中250组作为训练组，剩下50组作为测试组，求出PNN的故障输入矩阵I及故障模型输出向量Y后进行模型训练。

采用Matlab中的newpnn函数创建PNN，对前文所述方法进行仿真验证，将径向基函数的分布密度θ分别设为0.3，0.5，0.8，1.0对分类结果进行验证。

图3～图6为不同θ数值下，PNN对50组测试样本的实际分类结果与预期分类结果的对比图。其分类准确率如表2所示。

图3 θ=0.3故障分类结果

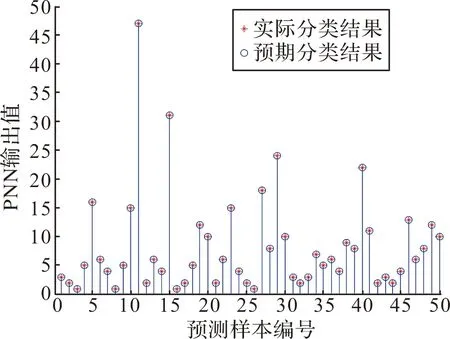
图4 θ=0.5故障分类结果

图5 θ=0.8故障分类结果

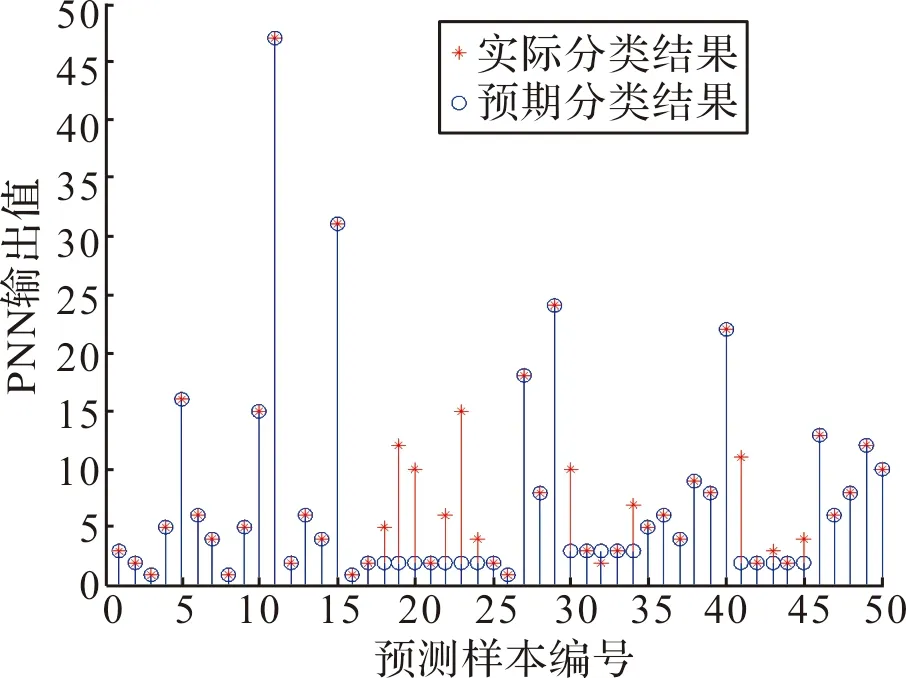
图6 θ=1.0故障分类结果

表2 PNN分类结果统计

从表2可知，θ越大，分类准确率越低，θ为0.3和0.5时，分类结果的准确率均为100%，均可满足对测试集样本故障分类的要求。但是参数θ的大小对网络逼近精度同样有很大影响[6]，θ越小，逼近的过程就越粗糙；θ越大，逼近过程就比较平滑[7]。因此θ取值为0.5时既可满足故障分类的准确率，也可确保逼近过程的平滑度。

3 结论

提出了一种基于PNN网络的故障诊断方法。该方法将测试数据由复杂的m×n矩阵转化为n维向量，简化了输入数据的分析规模；通过二进制到十进制之间的数据转换确立了故障输入与输出之间的唯一映射关系；最后利用PNN网络实现了多故障特征量下的故障分类。仿真结果验证了该方法的可行性和有效性，可以实现对弹载计算机的故障分类，且准确率满足要求。