带时间约束的双参数再入轨迹设计方法

2021-07-30白凤科杜凤怀

弹箭与制导学报 2021年3期

乔浩，毛瑞，白凤科，杜凤怀

(西安现代控制技术研究所，西安 710065)

0 引言

现有导弹飞行时间可控研究工作主要集中在常规战术导弹层面。2006年，Jeon等首先提出了针对反舰导弹命中时间可控的制导方法(impact-time-control guidance,ITCG)[1]，随后在该方法的基础上加入落角约束，提出同时考虑落角与命中时间的制导方法(impact-time-and-angle-control guidance,ITACG)[2]。2011年，Kang等对ITCC剩余时间的估计方法进行了改进，提出了一种同时满足落角与时间约束的微分对策制导方法，该方法将弹目之间的运动关系线性化，采用二次型性能指标函数先对落角约束进行优化求解，然后根据对剩余时间的估计修正制导指令，实现对落角与到达时间的控制[3]。2015年，Zhang等采用一种基于偏置比例导引的分布式协同制导方法，研究了多枚反舰导弹的同时攻击问题，并考虑了视场约束，在固定或切换通信网络中有较好的收敛性，对通信拓扑的要求降低[4]。与上述方法不同，Zhao等提出一种轨迹曲线矫正的方法，将寻的过程的轨迹定义为特定形式的多项式，通过调节系数控制导弹满足终端落角及时间约束，具有较好的几何意义[5]。

再入时间可控，是再入飞行新的应用场景，对未来战场环境有可能造成较大的影响。相对常规导弹而言，这方面的研究仍处于起步阶段，主要分为两种策略，一是通过航向偏差走廊进行控制，代表性的有双层航向偏差走廊方法与神经网络航向偏差走廊方法[6-7]；二是在设计参考轨迹时考虑飞行时间的要求，代表性的有基于解析剖面的时间协同方法[8]。由于航向偏差走廊本质上是一种侧向制导逻辑，并不能直接对飞行时间进行调节，文中在第二方法基础上对其中的轨迹设计方法进行改进，提出一种更为简洁的直接设计总飞行时间的参考轨迹生成方法。

1 再入问题描述

1.1 动力学模型

以能量为自变量将时间信息提取出来，对于含时间约束的再入问题尤为适用。假设飞行器为质点，地球为均匀球体，忽略地球自转。再入飞行器的总能量e定义为：

(1)

(2)

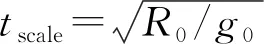
L=ρ(r)V2SACL(α,Ma(e,r))/2m

(3)

D=ρ(r)V2SACD(α,Ma(e,r))/2m

(4)

式中：ρ为大气密度；SA为飞行器参考面积;CL，CD分别为升力系数和阻力系数；m为飞行器质量。倾侧角σ使升力矢量位于竖直平面右侧(从飞行器尾部看去)时为正。

1.2 过程约束与再入走廊

再入飞行器一般具有很大的初始能量，在进入稠密大气层之后，飞行器与大气相互作用，产生严重的气动加热、气动过载及动压，相应的过程约束可描述为：

(5)

(6)

q=0.5ρV2≤qmax

(7)

(8)

上述约束是一种对再入安全性的宏观考量，不能保证飞行轨迹的平稳。因此一般将准平衡滑翔约束作为软约束，对应的阻力加速度下边界为：

(9)

上述两组约束共同构成了能量-阻力加速度空间内的再入走廊。

2 带时间约束的双参数轨迹设计

对于侧向机动较多的再入过程，大圆弧假设会造成较大的轨迹长度偏差，增加后续迭代次数，也容易错过倾侧角最佳符号反转位置。采用提前量化轨迹长度的方式，定义Pm为机动系数，以其与初始大圆弧Rl的乘积表示期望的实际轨迹长度，即：

Rflight=PmRl

(10)

在参考阻力加速度剖面中首先设定两个能量点E1，E2，各点对应的阻力加速度取值由再入走廊确定，记作[Ddown，Dup]；取两点的调节系数k1，k2∈[0,1]，则E1，E2对应的阻力加速度分别为：

(11)

对k1，k2进行搜索，获得同时满足轨迹长度与飞行时间的参考轨迹，如图1所示。

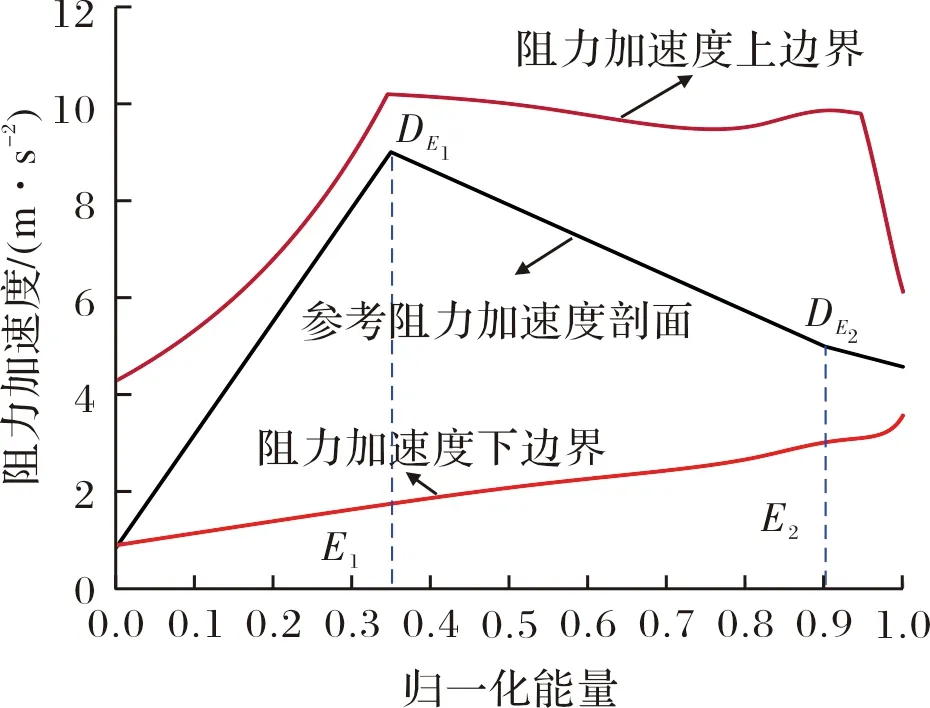
图1 双参数的阻力加速度剖面设计示意图

初始的阻力加速度D1与终端的阻力加速度D3由任务确定，此时对应的阻力加速度剖面为：

(12)

指定机动系数Pm与期望的飞行时间Treq，采用标称跟踪确定的实际轨迹长度Rreal与总飞行时间Treal作为预测值，可得总飞行时间与轨迹长度的偏差函数为：

(13)

此时问题转化为二元非线性方程组的求根问题[9]。

对于二元函数z=f(x,y)，假设其在(x0,y0)的邻域内连续且具有连续的二阶偏导，可得：

(14)

式中：h=x-x0，k=y-y0。将∂f(x,y)/∂x记作fx，同理对y的偏导记作fy，f(x,y)=0可近似为：

(15)

同理，对于二元函数z=g(x,y)，对应的二元非线性方程g(x,y)=0可近似为：

g(xk,yk)+(x-xk)gx(xk,yk)+

(y-yk)gy(xk,yk)=0

(16)

联立式(15)与式(16)，可得：

(17)

式(17)即二元函数的牛顿迭代法。对应文中待求变量为指定能量点的系数k1，k2。根据式(17)可得：

(18)

在实际求解过程中，飞行时间与轨迹长度的偏差可由全弹道积分获得，关于k1，k2的偏导需要采用有限差分进行求解。因此在迭代初期需要人为设定初始值，避免迭代失效。同时需要设置迭代的终止条件：|F|<ε1且|G|<ε2，避免无效运算。ε1，ε2分别为飞行时间与轨迹长度的允许偏差。上述求解过程等价于多元函数的极值问题，即搜索k1，k2使轨迹长度与飞行时间的加权性能指标最小：

J=ω1F2+(1-ω1)G2

(19)

式中，ω1为权重系数。在这种表示方法下，参数优化的牛顿迭代法同样可以用于调节系数k1，k2的求解。在获得满足轨迹长度与飞行时间的k1，k2之后，对应的参考阻力加速度剖面随即确定。

3 仿真分析

3.1 带时间约束的参考阻力加速度剖面迭代

直观上讲，在不考虑轨迹跳跃的情况下，当倾侧角指令增大，会增加高度方向的变化率，使朝向终端高度演化的时间缩短，总飞行时间呈现出减少的趋势；但另一方面，随着高度的降低，大气密度又会快速增加，导致气动阻力增大，飞行器飞向目标的速度变慢，总飞行时间又呈现出增加的趋势。可见，制导指令对于总飞行时间的影响机理是较为复杂的。以CAV-H为研究对象，其详细参数见文献[10]；攻角方案见文献[11]。以东向为0°航向角，逆时针旋转为正。设飞行器的初始位置为(0°,0°)，目标位置为(60°,0°)；初始与终端高度分别取60 km，28 km；初始与终端速度分别取6.8 km/s，1.8 km/s；设置末端能量管理区域的半径为sT=50 km；再入终端高度、速度、剩余航程的最大允许偏差分别为2 km，10 m/s，5 km；最大热流率取4 MW/m2，最大过载取3，最大动压取为70 kPa。根据再入走廊的分布情况，在可调节范围较大的区域选取校准点，取E1=0.35，E2=0.9。由于再入走廊的上边界对应了热流、过载与动压这类硬约束，因此在飞行过程中应保留一定裕度，对两个校正点处的阻力加速度取值范围进行限制，有：DE1∈[1.8, 9]，DE2∈[1.8, 9]。指定机动系数Pm=1.02，期望飞行时间Treq=1400 s，取权重系数ω1=0.5，此时对应的参考阻力加速度剖面迭代过程如图2所示，由上、下边界迅速向搜索结果收敛。

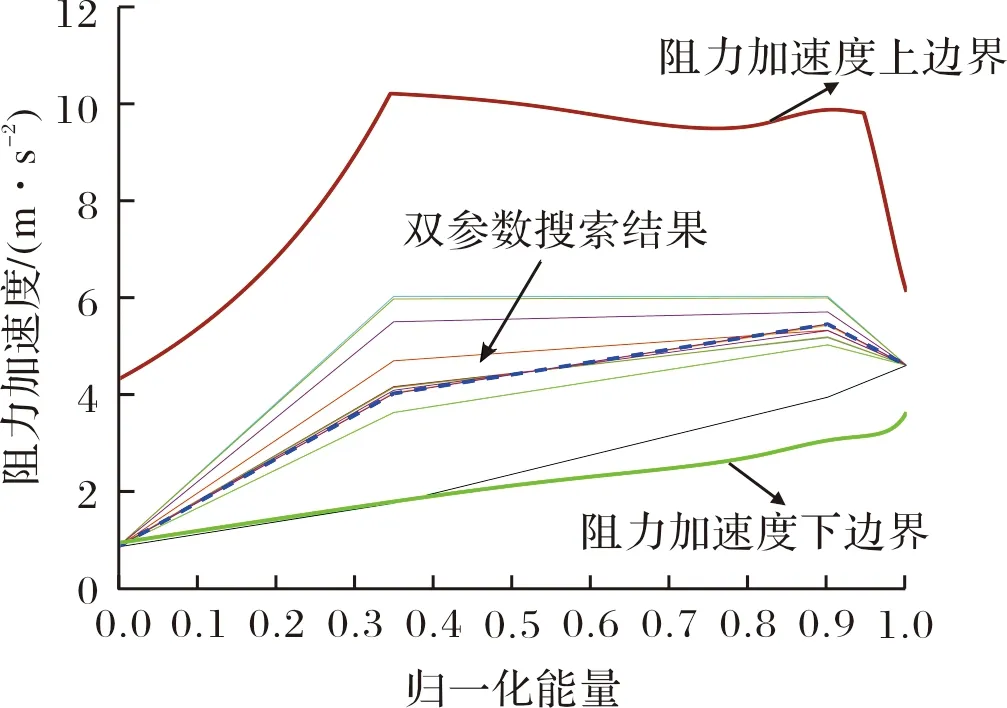
图2 双参数的阻力加速度剖面迭代过程

其中，DE1=3.9944 m/s2，DE2=5.4267 m/s2，总飞行时间偏差F=-4.534×10-5s，轨迹长度偏差G=-2.4046 m。可见，双参数的参考阻力加速度剖面生成方法能够很好满足轨迹长度与飞行时间的需求。

3.2 多任务场景仿真测试

为增加总飞行时间调节规律分析结果的可靠性，进一步增加任务场景，对参考阻力加速度剖面的形式与总飞行时间的对应关系做更深入的分析。对机动系数Pm=1.02分别设置Treq为1 350 s，1 400 s，1 450 s，对应的仿真结果如图3～图7所示。

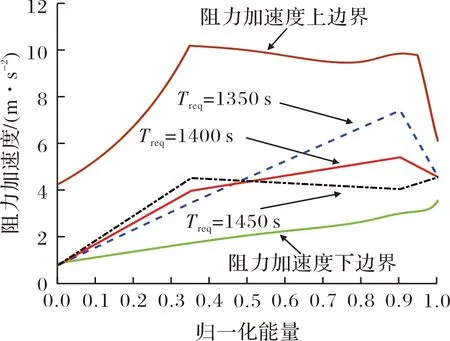
图3 阻力加速度剖面搜索结果

图4 地面轨迹投影

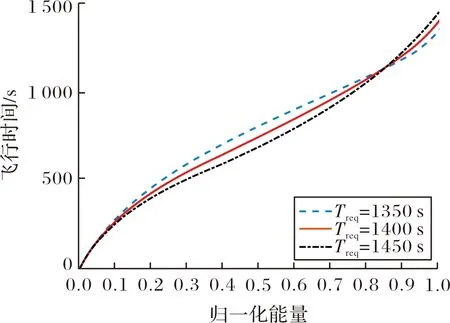
图5 飞行时间演化曲线

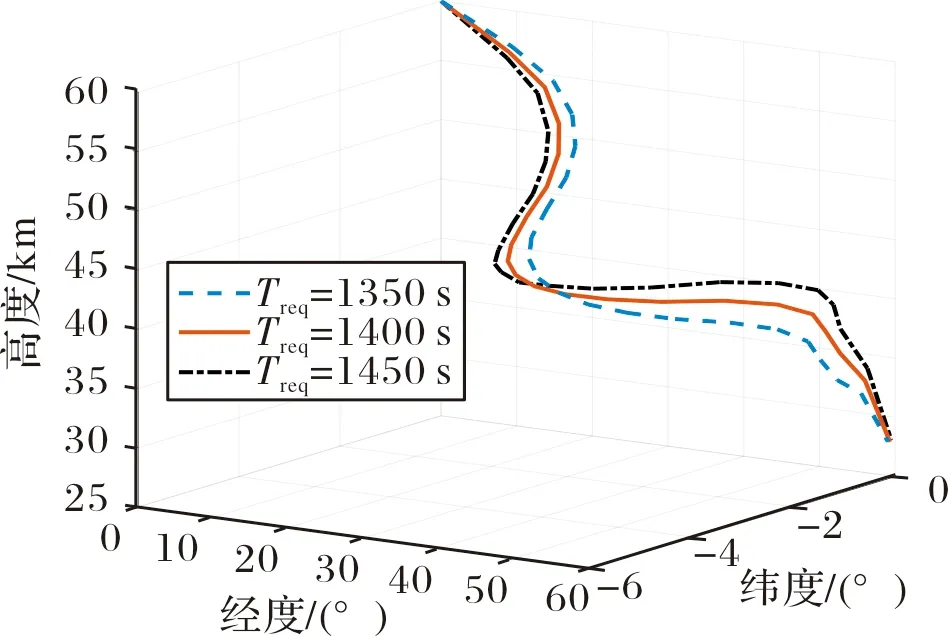
图6 三维轨迹

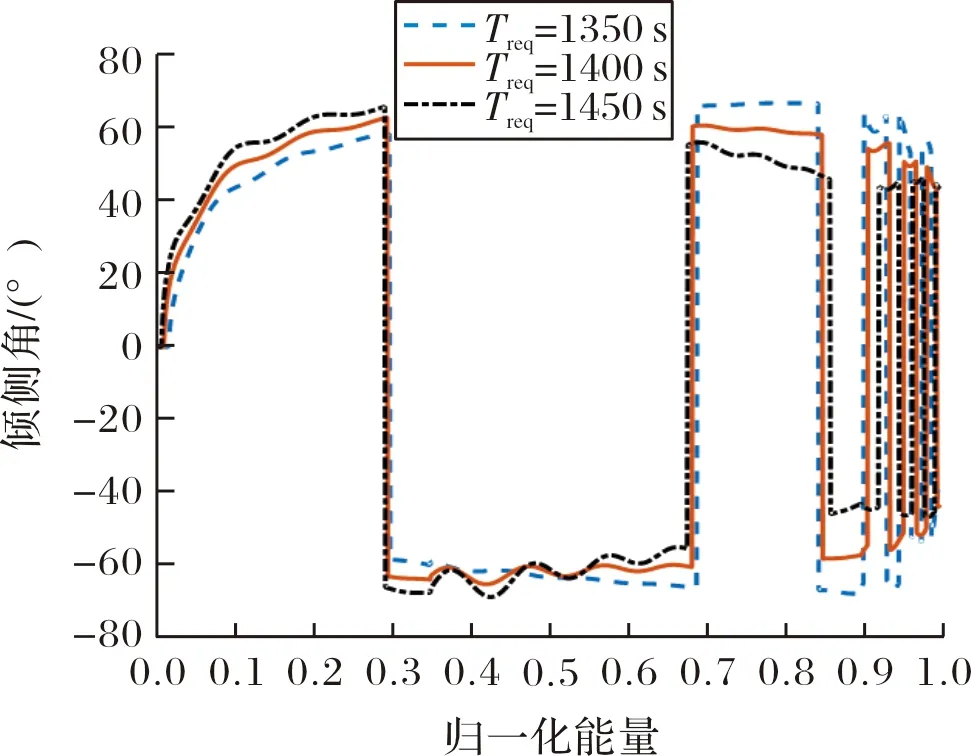
图7 标称跟踪对应的倾侧角指令

可以看出，不同期望飞行时间Treq对应的参考阻力加速度剖面具有一定的规律，即：Treq越小，第一个校正点E1处的阻力加速度越小，而在第二个校正点E2处的阻力加速度越大，此时飞行器以相对最速到达的方式飞行；Treq越大，两个校正点上的阻力加速度分布与最速到达恰好相反，飞行器前期以较大的阻力加速度飞行，后期阻力加速度逐渐减小。从倾侧角指令的分布情况可以看出，在归一化能量0.5之前，最慢到达的倾侧角幅值最大，在这之后，最慢到达对应的倾侧角幅值最小。

综上可知：对于初始位置与目标给定的飞行任务，当期望的飞行时间Treq较大时，飞行器首先应采用幅值较大的倾侧角，使纵向平面内的气动力分量减小，飞行器快速掉高，进入大气较为稠密的高度区间，此时飞行器减速加快，飞行速度相对变慢，到达目标所需的时间增加，后期倾侧角幅值变小主要是为了弥补前期掉高造成的轨迹长度不足，飞行器以更接近准平衡滑翔的方式接近目标，在接近目标区域上方进行轨迹下压；当希望飞行器较快到达目标时，再入初期应采用幅值较小的倾侧角指令，使飞行器以较高的轨迹飞行，减小速度衰减，直至最终接近终端区域，通过增大倾侧角幅值的方式完成轨迹快速下压，以匹配相应的轨迹长度约束。