两栖车航行间发射动力学研究
2021-07-30李玉龙
余 浩,李玉龙,姜 毅
(1 北京理工大学宇航学院,北京 100081;2 96901部队,北京 100094)
0 引言
随着我国军事实力的提升与发展,两栖火炮战车具有机动性好、可实现水陆两栖作战、隐蔽性强的优点,但受制于火炮射程的限制,其打击范围以及打击精度有限,在某些情况下难以满足军事需求,而导弹则在射击精度及射程上较火炮具有一定的优越性,两栖导弹发射车的概念也就应运而生。以两栖战车作为导弹的发射平台,不仅具有良好的机动性,同时也保障了打击的射程与精度,但目前对于两栖导弹发射车的研究相对较少。因此,对于两栖导弹发射车的相关研究就显得较为迫切。
马广松对两栖火炮发射稳定性进行了研究,但仅仅研究了静水条件下的发射动力学问题[1]。蒋华剑等通过建立某两栖自行火炮的横向发射动力学模型,得出应避免小射角射击以提高射击稳定性的结论[2];刘云等对两栖车的水上行驶过程进行了仿真[3];王蕾等采用两种改进方法对海浪进行了数值模拟[4]。
文中以某型两栖车为对象,对其进行受力分析,基于单参数Pierson-Moscowitz谱生成随机海浪激励,利用多体动力学软件建立了两栖车海上航行发射导弹的多刚体动力学模型,通过多次仿真得到了导弹出筒姿态的分布规律,以及海平面上19.5 m高处的平均风速、两栖战车航速以及航向角等因素对导弹出筒姿态角以及角速度的影响。
1 两栖战车行进间发射动力学模型
1.1 模型假设
当两栖车于水上行驶时,两栖车车体结构稳定,车轮、前滑板以及后滑板等组成部分主要影响车体流体外形,均无明显的变形以及相对于车体主体的位移,因而车体所产生的形变对于行进间发射动力学响应基本可以忽略。同时,不考虑发射装置以及导弹的形变,故假设整个模型为刚体。
导弹发射过程持续时间较短,约为0.8 s,因此弹射过程中发射系统质量变化对于发射动力学响应影响可忽略。
基于成熟的两栖车及船舶相关理论知识,主要考虑两栖战车的升沉、纵摇以及横摇;不考虑连接处摩擦,假定为理想连接。
两栖车在水上行驶时所受到海浪激励载荷远大于所受风载荷,导弹在弹射过程中与发射筒之间作用力也远大于其所受风载荷影响。因此,主要考虑海浪激励载荷,忽略风载荷影响。
1.2 坐标系说明
如图1所示,两栖车主要由车体、发射架、发射筒以及导弹4部分组成。规定全局坐标系的Z轴负方向与重力作用方向相同,X轴负方向为车辆行进方向,Y轴正方向可用右手螺旋定则确定。
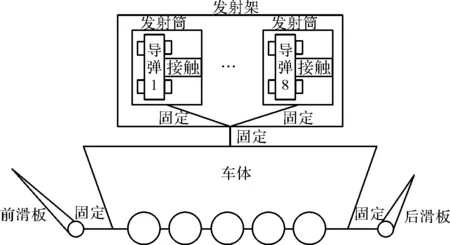
图1 两栖车拓扑连接图
两栖车采用垂直弹射方式进行单发导弹发射。定义导弹绕X轴转角为偏航角θx,绕Y轴转角为俯仰角θy,绕Z轴转角为滚转角θz;绕X轴角速度为偏航角速度ωx;绕Y轴角速度为俯仰角速度ωy;绕Z轴角速度为滚转角速度ωz。
1.3 车体受力分析
除重力外,两栖车主要受到的力与力矩有[5]:海浪干扰力与力矩,航行推力与航行阻力,浮力与浮力矩,流体阻尼力与阻尼力矩,附加质量力与附加质量力矩,弹射反作用力。
1.3.1 海浪激励
根据单参数Pierson-Moscowitz谱,可以得到随机海浪波面升高能量谱密度函数Sζ(ω)和随机海浪波倾角能量谱密度函数Sα(ω):
(1)
(2)
式中:a,b均为系数,一般取a=8.1×10-3,b=0.74;U为在海面上19.5 m高处的平均风速;ω为波浪圆频率;g为重力加速度,一般取9.81 m/s2。
理论上海浪频谱分布为0~∞,但大量经验表明:各种海浪的能量主要集中于一特定频段,故可取能量增量Δω,在特定频段内进行等间隔采样。利用谐波叠加法,可得随机海浪波面升高ζ(t)和随机海浪波倾角α(t):
(3)
(4)

引入波的遭遇频率ωe:
(5)
式中:v0为两栖车航行速度;γ为航向角。
结合式(3)和式(4),得到引入航速、航向的随机海浪遭遇波面升高和遭遇波倾角:
(6)
(7)
将式(7)在车体横摇以及纵摇方向上分解,得车辆遭遇横摇波倾角αeφ(t)和车辆遭遇纵摇波倾角αeθ(t):
(8)
(9)
由式(6)~式(9)得到作用于车体质心的海浪垂向扰动力Zs、车体所受海浪横摇扰动力矩Ks和纵摇扰动力矩Ms:
(10)
(11)
(12)
式中:kz,kφ,kθ分别为车辆在垂向、横摇方向和纵摇方向上的弹性系数;nz,nφ,nθ分别为车辆在垂向、横摇方向和纵摇方向上的阻尼系数;mw为被扰动的水的质量;ix,iy分别为被扰动的水的转动惯量在车辆横摇方向和纵摇方向上的分量。
1.3.2 航行推力与航行阻力
为模拟两栖车航行的动态过程,在两栖车航行方向施加航行推力T与航行阻力R:
T=T0-txu
(13)
R=nuuW
(14)
式中:T0为拖桩牵引力;tx为推力速降系数;u为航速;nu为车辆在航行方向的阻尼;W为车辆在航行方向的阻尼nu与航速u的方幂系数。当航行推力与航行阻力相等时,两栖车航行速度为定值。
1.3.3 浮力与浮力矩
浮力F作用方向竖直向上,浮力矩则作用于车体质心,并向车体横摇方向和纵摇方向进行分解,分别记为Mφ及Mθ:
F=ρgV
(15)
Mφ=Fhφφ
(16)
Mθ=Fhθθ
(17)
式中:V为车体排开水的体积;hφ,hθ分别为车体横稳心半径以及纵稳心半径;φ,θ分别为车体横摇角及纵摇角。
1.3.4 流体阻尼力及阻尼力矩

Fz=nzw
(18)
(19)
(20)

1.3.5 附加质量力与附加质量力矩
附加质量力Fmw沿竖直方向,附加质量力矩分别向车体横摇方向以及纵摇方向分解,分别记为Mmφ,Mmθ:
Fmw=mwa
(21)
(22)
(23)
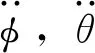
1.3.6 弹射力激励
弹射力经内弹道计算给出,作用于导弹质心,方向沿发射筒壁向外,弹射反作用力作用于发射筒底部中心,与弹射力方向相反。
2 仿真计算与分析
2.1 导弹出筒姿态分布规律研究
由于海浪对发射系统的激励具有随机性,因此仅凭单次仿真结果难以探究导弹出筒姿态角以及角速度的分布规律。故通过编写程序生成用于进行多次仿真的批处理文件以及脚本文件,以导弹发射时间为仿真变量,对每一种工况进行多次仿真,最终得到基于多次仿真的统计结果。
由于仿真结果中,导弹出筒滚转角θz以及滚转角速度ωz相较于其他出筒姿态角及角速度为极小量,仅列出导弹出筒偏航角θx、俯仰角θy、偏航角速度ωx以及俯仰角速度ωy的统计结果。
图2~图5为两栖车在航速v=25 km/h,航向角γ=120°,海面上19.5 m高处的平均风速U=7.9 m/s下行进间进行发射,导弹的θx,θy,ωx以及ωy的仿真结果频数分布直方图。
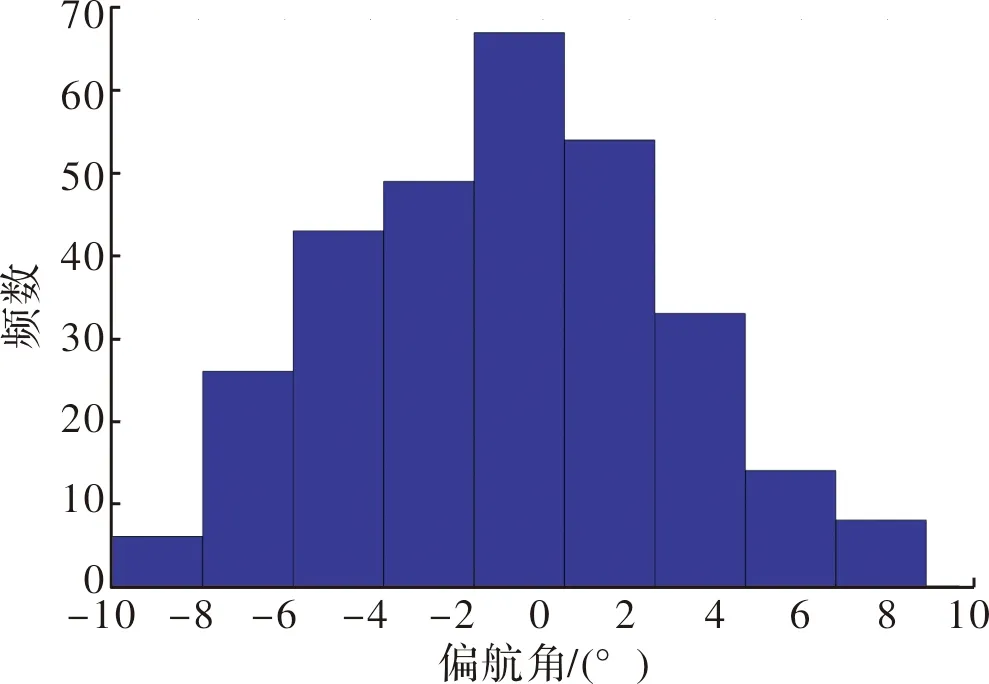
图2 偏航角频数分布直方图
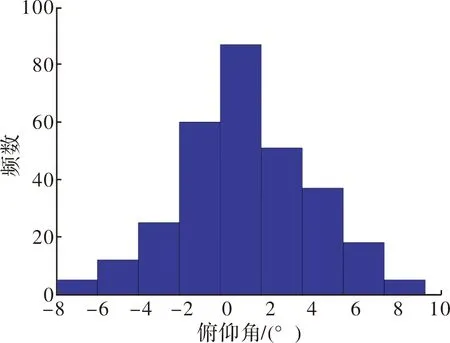
图3 俯仰角频数分布直方图

图4 偏航角速度频数分布直方图
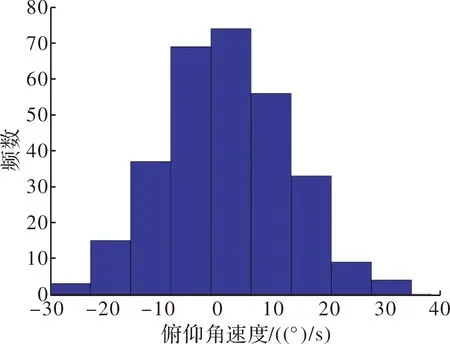
图5 俯仰角速度频数分布直方图
由图2~图5可以看出,在同一工况下,导弹出筒姿态角以及角速度的分布近似呈正态分布。图6给出了导弹出筒偏航角的概率密度曲线与频数直方图的对比图。
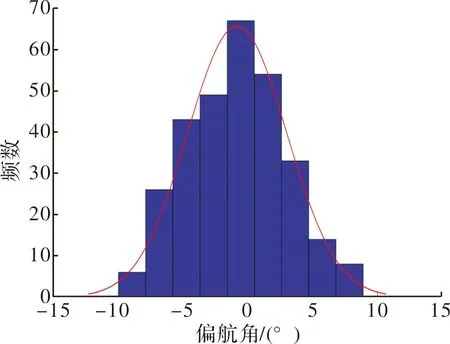
图6 偏航角概率密度曲线与频数分布直方图对比图
从多个工况仿真计算的统计结果来看,导弹的出筒姿态角以及角速度分布与正态分布均有良好的符合度。因此可以得出结论,两栖车行进间进行导弹发射,其导弹的出筒姿态角以及角速度分布均呈正态分布。
2.2 导弹出筒姿态影响因素研究
为探究海平面上19.5 m高处的平均风速U、两栖车航速v以及航向角γ对导弹出筒姿态的影响,分别以平均风速U、两栖车航速v以及航向角γ为变量,设计了多种工况,并进行多次动力学仿真,利用批处理得到了相关的统计结果。表1~表5分别给出了以海平面上19.5 m高处平均风速U以及两栖车航速v为变量进行计算的计算结果。图8~图9给出了U=7.9 m/s,v=25 km/h下导弹出筒姿态角和角速度均方根值随航向角变化折线图。
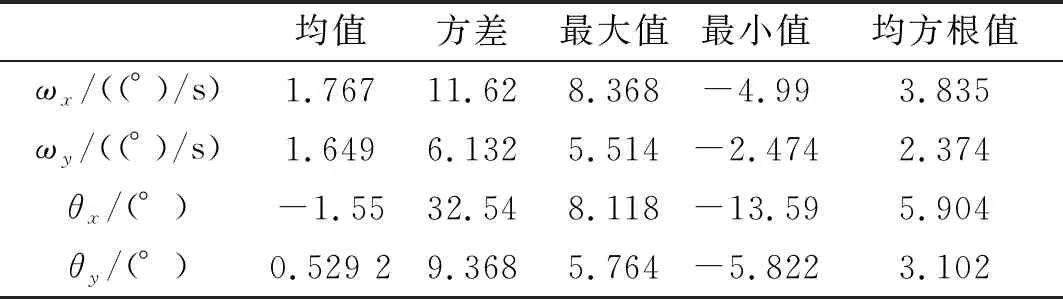
表1 γ=60°,v=25 km/h,U=7.9 m/s时计算结果

表2 γ=60°,v=25 km/h,U=6 m/s时计算结果

表3 γ=60°,v=25 km/h,U=4 m/s时计算结果
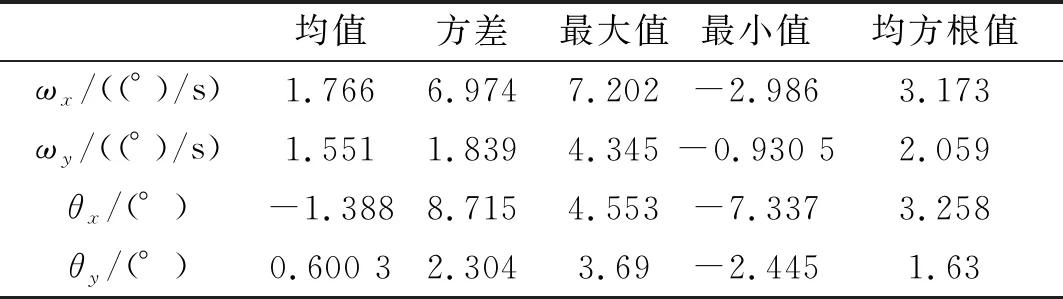
表4 γ=60°,v=18 km/h,U=7.9 m/s时计算结果
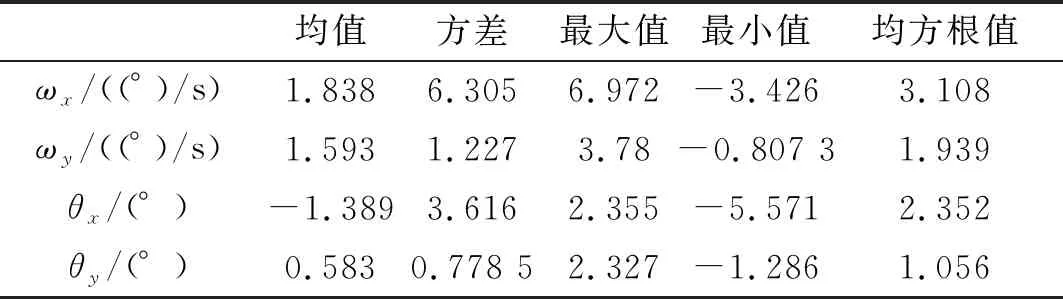
表5 γ=60°,v=10.8 km/h,U=7.9 m/s时计算结果
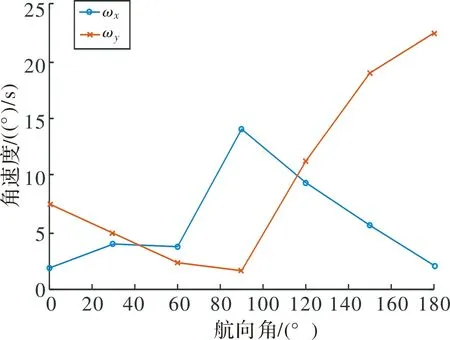
图8 姿态角速度均方根值随航向角变化折线图
由表1~表5可以看出,随着海平面上19.5 m处平均风速U以及两栖车航速的增大,导弹出筒姿态角、姿态角速度方差及均方根值也随之增大。因此,海平面上19.5 m处平均风速越高,两栖车航速越大,导弹出筒姿态越恶劣。
由图7~图8可得,导弹出筒偏航角θx以及偏航角速度ωx均方根值随着航向角增加先增大后减小,导弹出筒俯仰角θy以及俯仰角速度ωy均方根值随着航向角增加先增大后减小,均在航向角γ=90°时出现极值。显然当两栖战车尾斜浪(30°≤γ≤60°)航行时进行发射,导弹出筒姿态角以及角速度均处在一个较好的水平。而当航向角γ≥90°时,导弹出筒姿态角速度较为恶劣,因此两栖车应避免在此情况下进行导弹发射。
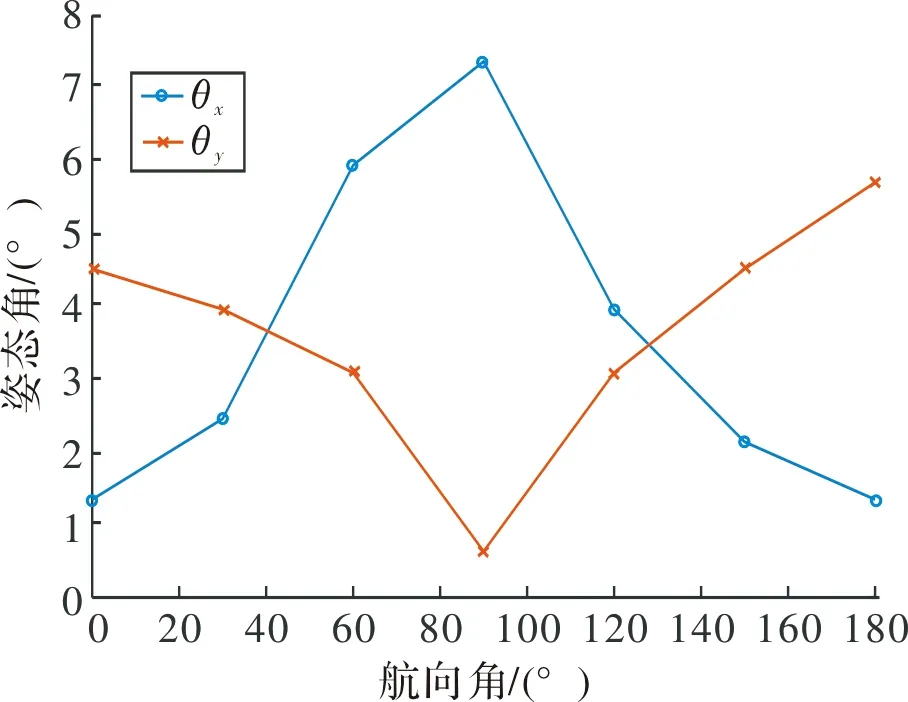
图7 姿态角均方根值随航向角变化折线图
3 结论
根据单参数Pierson-Moscowitz谱,利用谐波叠加法生成随机海浪激励,建立了两栖车行进间多刚体发射动力学模型,对两栖车发射导弹的出筒姿态分布规律及影响因素进行了研究,得到如下结论:
1)两栖车行进间进行发射,其导弹的出筒姿态角以及角速度分布符合正态分布。
2)海平面上19.5 m处平均风速及两栖车航行速度越小,导弹出筒姿态越好。
3)两栖车航向角在0°~180°范围内变化时,导弹出筒偏航角以及偏航角速度均方根值随着航向角增加先增大后减小,导弹出筒俯仰角θy以及俯仰角速度ωy均方根值随着航向角增加先增大后减小,均在航向角γ=90°时出现极值。因此,两栖车在尾斜浪航行时进行发射,发射安全性较高。
