喷动床粉体混合机混合性能的数值模拟

2021-07-29王一泽熊桂龙苏文康刘振峰

南昌大学学报（工科版） 2021年2期

王一泽，熊桂龙，苏文康，刘振峰

( 1.南昌大学a.资源环境与化工学院；b.鄱阳湖环境与资源利用教育部重点实验室，江西南昌 330031；2.宜春万申制药机械有限公司，江西宜春 336000)

离散物料的混合设备主要有两大类：机械式混合设备与气力式混合设备[1]。与传统的机械式混合设备相比，气力式粉体混合机具有混合体积大、均匀性好、能耗低、密闭无泄漏、清洁环保等优点，在能源、化工、制药，食品等行业领域应用广泛[2-3]。气力式混合设备主要有喷动床、流化床混合设备，其工作原理是通过压缩空气使离散物料流态化并向上膨胀，压缩空气膨胀到一定程度后物料由于重力作用向下沉降，离散物料在气流作用下产生上下翻滚和激烈的沸腾搅拌，在相对较短的时间内达到混合均匀[4-5]。因此，对喷动床粉体混合机的粉体混合过程及运动行为规律进行分析具有重要意义。

对于喷动床粉体混合的研究常采用实验方法与数值模拟的手段，但由于受到实验条件与设备的限制，通过实验难以获得颗粒微观尺度上的全面运动信息，例如颗粒速度、颗粒混合质量、基于颗粒尺度的碰撞信息等。随着计算机技术快速发展，数值模拟在研究气固两相流动问题的优势日益凸显，可以获得更为全面的颗粒运动信息[6-7]。李斌等[8]采用CFD-DEM耦合的数值模拟方法对循环流化床内颗粒的混合行为进行了研究，认为增大流化风速有助于加速颗粒混合。张俊强等[9-10]采用数值模拟的方法分别研究了单孔与双孔射流流化床颗粒的混合效果，结果表明，颗粒的轴向混合速率大于径向混合速率。陈程等[11]基于CFD-DEM的方法对旋转流化床粉体混合机进行了研究，结果表明，进气管倾斜一定角度布置，可全面提高混合强度。Sharma等[12]对鼓泡流化床内不同颗粒的混合与分离过程进行了数值模拟。Olaofe等[13]采用数值模拟的方法研究了流化床内气固两相运动特性，分析了颗粒在气流作用下的混合过程。Ren等[14]采用数值模拟的方法对喷动床中不同密度颗粒的混合行为进行了研究，研究结果表明，随着颗粒密度差的增大，粉体混合均匀性指数增大。已有的研究大多以实验室小规模装置为研究对象，所用的颗粒大多为毫米级，然而，在实际工业过程中设备的尺寸相对较大、颗粒的粒度较小，颗粒粒径通常在微米或亚微米的数量级，颗粒数量较大，对实际工程尺度的喷动床进行数值模拟研究是喷动床粉体混合研究的热点与难点。

本文采用数值模拟的方法对工业级喷动粉体混合机中直径为165 μm的同种淀粉颗粒混合过程进行了研究，根据相似原理与流动相似理论，对颗粒直径进行了工程缩放，以减少颗粒数量，降低计算资源与计算量。建立了喷动床中粉体混合的模型，分析了喷动床中粉体微观混合过程，喷动床中气体与颗粒沿床宽和床高方向的速度分布，颗粒循环运动周期，评价粉体混合均匀性的混合指数，为工业级喷动床粉体混合机的研发与应用提供理论基础与参考。

1 数值模拟

1.1 模型建立

喷动床粉体混合机的几何模型和流体网格模型如图1(a)～(c)所示，采用底部轴向进气，顶部为出气口，坐标原点设置在底部的圆心处，初始粉体堆积状态如图1(a)所示，床层表面颗粒1与床层底部颗粒2的比例为1:10；喷动床几何尺寸参数如图1(b)与表1所示；喷动床中流体运动区域的网格划分采用结构化网格，流体网格模型如图1(c)所示，经网格无关性验证后，最终Fluent网格划分的节点数为45 903，网格数37 660。

(a) 喷动床结构图 (b) 几何尺寸

表1 喷动床几何尺寸参数Tab.1 Geometry parameters of spouted bed

1.2 数学模型

1.2.1 流体相控制方程

对于不可压缩流体，利用N-S方程来描述气相的流动，连续性方程和动量方程分别为：

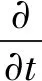
(1)

(2)

式中：ρf为流体密度，ρf=1.205 kg·m-3；αf为空隙率；p为压力；uf为流体速度；τ为应力张量；Fpf为颗粒相与流体相的动量交换。

1.2.2 颗粒相控制方程

暮色四合，潼关泣血，天策府的女将军曹雪阳绰长枪，领着将士们百战断头，蹚在血海里，奋力杀贼，饶是如此，也难挽哥舒翰力战败北，归降安禄山。大战之余，朗朗晴天风云变幻，电闪雷鸣中，暴雨如注，荡涤谷中血肉，将数十万腥臭的尸骨冲进黄河。大唐经此一役，由盛转衰，奄忽百年遂亡，这是后话不提。

采用离散单元法对颗粒相进行模拟计算，该方法可描述系统中的每个单个粒子i通过接触力Fc,ij与其他粒子或壁面j的相互作用。接触力Fc,ij可以被分解为法向分力Fn,ij和切向分力Ft,ij。颗粒运动过程中所受的力主要包括：重力、颗粒之间、颗粒与壁面间的接触力、摩擦力、曳力、浮力。颗粒的运动包括平动和转动，由牛顿第二定律确定[15]：

(3)

(4)

式中：mp,i、Ip,i分别为颗粒i的质量、转动惯量；vp,i、ωp,i分别为颗粒的平动速度、转动速度；Fg,i和Ff,i分别表示颗粒重力和气相对颗粒的作用力；Tt,ij和Tr,ij分别是由切向力和滚动摩擦产生的扭矩。颗粒间接触采用Hertz-Mindlin模型。

1.2.3 曳力模型

气体对颗粒的曳力Fd,i采用Gidaspow曳力模型，在空隙率αf>0.8时，颗粒的曳力计算方程为：

(5)

在空隙率αf≤0.8时，颗粒的曳力计算方程为：

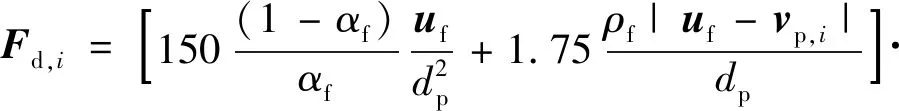
(6)

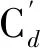
Cd为单个颗粒的曳力系数，其取值与颗粒雷诺数Rep有关，Rep≤1 000时，Cd计算方程为：

(7)

当Rep=1 000时，

Cd=0.4

(8)

粉体物料混合后，其混合的均匀性可采用目前国内外使用较多的Lacey指数[11]来表征与评价，当粉体处于完全分离的状态时，Lacey指数为0，粉体在理想混合均匀状态时，Lacey指数为1，在实际混合过程中，Lacey指数在0～1之间变化，因此，可以利用Lacey指数的变化来分析粉体在整个喷动过程中的混合情况。表征粉体混合均匀性的Lacey指数为：

(9)

(10)

(11)

(12)

式中：P为一种颗粒所占比例；(1-P)为另一种颗粒所占比例；n为每一个样本内平均颗粒数量；NS为样本总数；ai为两类颗粒中任意一类在样本i中所占的比例；a为相应的颗粒在喷动床中所占比例；ki为样本i的权重，表示为：

(13)

(14)

式中:Ni为样本i内的颗粒数；Nt为颗粒数总和。

1.3 模型参数

颗粒系统中有两种颗粒，初始堆积状态下床层表面淀粉颗粒1的质量5 kg，床层底部淀粉颗粒2的质量为50 kg，两种颗粒总数量为146亿个，颗粒直径为165 μm，颗粒密度为1 600 kg·m-3。气流进口边界条件设为速度进口，并采用UDF函数控制入口处气流速度，前5 s为匀加速进气状态，初速度为0 m·s-1，加速度为1 m·s-2，在第5秒时入口处进气速度达到并稳定在5 m·s-1，直到第30秒时停止进气；气流出口边界条件设置为一个标准大气压。为了减小计算量，缩短计算时间，基于相似原理与流动相似理论进行工程缩放，在工程缩放过程中，保证颗粒总体积、颗粒最小流化速度Umf、颗粒雷诺数Rep、阿基米德数Ar为常数不变[16-18]，可将计算的粒子总数Np由146亿个减少到128 227个。

为了保证缩放前后颗粒床层体积的相似性，缩放后的颗粒直径可由下式得到：

(15)

式中:mbed、N、ρp、dp分别为颗粒床层总质量、颗粒数目、颗粒密度和颗粒直径。下角标1和2分别为初始颗粒系统与缩放后的颗粒系统。

缩放因子kc可由下式得到：

(16)

对于缩放前后的系统，气体密度ρg和重力加速度g保持不变。

在数值模拟计算中，DEM时间步长为10 μs，CFD时间步长为500 μs，颗粒与颗粒间发生碰撞时恢复系数、静摩擦系数、滚动摩擦系数分别为0.75、0.5、0.06，颗粒与壁面间发生碰撞时恢复系数、静摩擦系数、滚动摩擦系数分别为0.8、0.3、0.05。缩放前后的颗粒与气体的相关参数如表2所示。计算中所需的其他参数设置如表3所示。

表2 缩放前后颗粒和气体的参数Tab.2 Parameters of particles and gases before and after scaling

表3 模拟参数设置Tab.3 Simulation parameter setting

采用EDEM2017与Fluent17.0耦合的方法，通过UDF(用户自定义函数)实现耦合，模拟计算粒子运动与气相流场，离散相可以与流体相交换动量、质量和能量。

2 结果与讨论

2.1 粉体的混合过程

图2(a)～(f)是在不同时刻的喷动床混合机中粉体的混合过程，模拟时长共31 s。初始状态下，床层底部淀粉颗粒2与床层表面淀粉颗粒1的体积比为10:1。

(a) t=0.32 s (b) t=5 s (c) t=9 s (d) t=13 s (e) t=19 s (f) t=31 s

由图2(a)～(f)的混合过程可看出，根据喷动床中粉体的运动特征，喷动床可划分为喷射区、喷泉区、环隙区。从图2(a)可看出，在第0.32秒时刻，粉体颗粒依然处于初始堆积状态，两种粉体颗粒之间有明显的分层；随着床层底部进口气流速度的增大，喷动床底部气体压强增大，床层开始向上膨胀，如图2(b)所示；当进口气体流速在第5秒时刻达到5 m·s-1并稳定之后，喷射区逐渐形成，喷动气体开始穿透粉体床层，喷动床层底部的粉体开始在气流曳力作用下向上运动，粉体在向上运动的过程中会与周围粉体发生相互碰撞；从图2(c)可看出，当向上运动粉体在到达喷泉区时，在气流和其他粉体的碰撞作用下，喷泉区的粉体开始向四周扩散并向下运动；从图2(d)可知，粉体在喷泉区会发生强烈的混合，环隙区的粉体颗粒运动较缓慢，混合程度较弱，由图2(e)可知，当向下运动的粉体沉降到床层表面时，由于粉体所受重力大于流体曳力，粉体沿壁面向下运动，之后粉体从环隙区进入喷射区，在气体曳力作用下又重新向上运动，形成一个完整的循环运动过程。在循环运动的过程中最终达到粉体混合的动态平衡，如图2(f)所示。

2.2 粉体与气流速度分布

图3为喷动床达到稳定喷动时，在YOZ平面床层高度分别为0.2、0.4、0.6、0.8、1.0 m的粉体轴向速度和径向速度沿床层宽度的分布，轴向速度正方向和Z轴正方向一致，径向速度正方向和Y轴正方向一致。

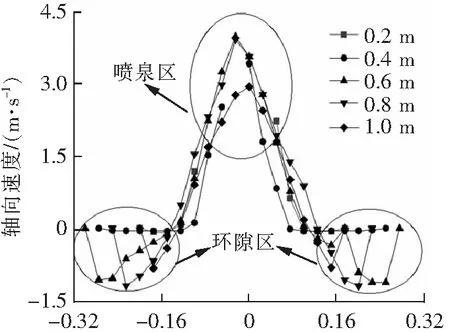
床宽/m(a) 粉体轴向速度

由图3(a)粉体轴向速度分布可知，喷射区不同高度处粉体的轴向速度为正值，该区域粉体向上运动，并且粉体轴向速度随着床层高度的增加先增加后减小，因为在喷射区床层高度为0.2 m时，粉体受到气体曳力作用加速运动，此时粉体轴向速度小于流体轴向速度，曳力为动力；当床层高度为1.0 m时，粉体轴向速度大于气体轴向速度，此时曳力为阻力，粉体减速运动。在环隙区的粉体轴向速度为负值，粉体向下运动，壁面附近粉体的流动性差，其轴向速度越小。由图3(b)粉体径向速度分布可知，床层高度为0.2～0.4 m时，喷射区左侧粉体径向速度为正值，粉体向右运动进入喷射区；右侧粉体径向速度为负值，粉体向左运动。床层高度为0.6～1.0 m时，喷射区左侧粉体径向速度为负值，粉体向左运动，离开喷泉区后向四周扩散，且粉体径向速度随高度的降低而增大；喷射区右侧粉体径向速度为正值，粉体向右运动。由此可知，在喷射区粉体受到气体的卷吸作用不断向中间聚集，之后在气流作用下向上运动，在喷泉区粉体不断混合，之后向四周扩散，在重力作用下向下运动进入环隙区，与环隙区的粉体重新混合后向喷射区运动，如此循环反复，粉体混合程度不断加深。

图4为喷动床形成稳定喷动后，在YOZ平面床层高度分别为0.2、0.4、0.6、0.8、1.0 m的气流运动的轴向速度和径向速度沿床层宽度的分布。

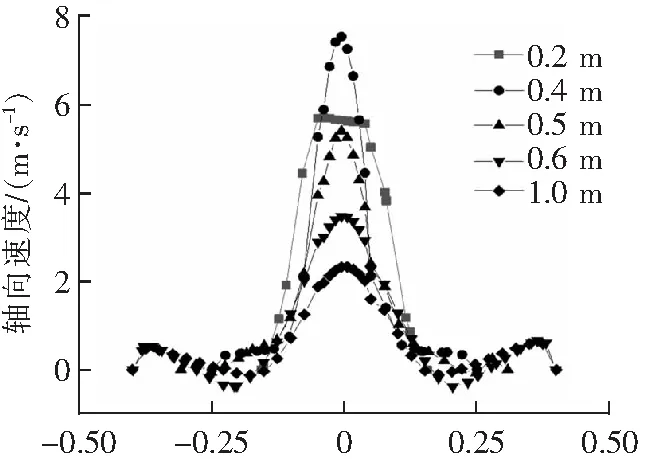
床宽/m(a) 气流轴向速度

由图4可知，在轴向上，喷射区气流向上运动，环隙区的气流向下流动；随着床层高度的增加，在喷射区气流轴向速度先增大后减小。沿径向床层底部气流向喷射区流动而喷泉区气体向四周扩散。由图3和图4对比可知，粉体与气流的分布规律相似，这也证明气流曳力作用下的粉体运动是影响喷动床粉体混合的主要原因，此外，气流轴向速度大于粉体轴向速度，流体动能转化为粉体动能和流体穿透床层的压力能。

2.3 粉体的循环运动周期

粉体在喷动床中依次经过喷射区、喷泉区和环隙区，做周期性的循环运动，其循环运动周期可定义为颗粒完成从床层表面开始向上运动，经过喷泉区，然后向下经过环隙区，然后进入喷射区并回到床层表面所需要的时间。为了分析粉体在每个循环周期内的运动过程，分别提取了床层表面颗粒1与床层底部颗粒2的空间位置随时间的变化，如图5所示。

图5 颗粒的三维空间坐标随时间的变化Fig.5 Changes of particle's three-dimensional space coordinates over time

由图5可知，床层底部颗粒2在第5.2秒时从床层表面开始向上运动，其在Z向的坐标值快速增大，运动至喷泉区，在第6秒左右的时刻，回落床层表面，进入环隙区，在第14.6秒左右的时刻，进入喷射区重新上升至床层表面，经历了一个完整的循环运动，其循环运动的周期约为9.4 s。其中，粉体在环隙区运动的时间为8.6 s，占整个循环运动周期的90%以上。颗粒1在第12.4秒时，完成第1次循环运动，颗粒2在第14.6秒时，完成第1次循环运动，床层表面和床层底部的粉体循环周期相差约2 s左右。颗粒1与颗粒2在第5.2秒时，进入喷泉区向四周扩散，其对应的X向与Y向坐标值突然增大；在从环隙区运动至喷射区的过程中，其对应的X与Y向坐标值会突然减小。在整个模拟计算时长内，粉体颗粒大约经历了3个循环运动周期：第1个运动周期在第14秒左右的时刻结束；第2个运动周期在第23秒左右的时刻结束；第3个运动周期在第30秒左右的时刻结束。由上述分析可知，颗粒在喷动床中循环运动周期约为9.4 s，在循环运动的过程中粉体不断混合并最终达到动态平衡。

2.4 粉体混合的均匀性

在粉体颗粒混合操作过程完成后，可利用大小一致的立方体虚拟网格对混合后的粉体区域进行划分。网格大小对Lacey指数有较大影响，因此，需选择合适的网格大小。如图6(a)所示，分别采用边长为32、40、50 mm的立方体虚拟网格进行划分，并对相应的混合均匀性指数进行计算，提取混合均匀性指数随时间的变化规律。

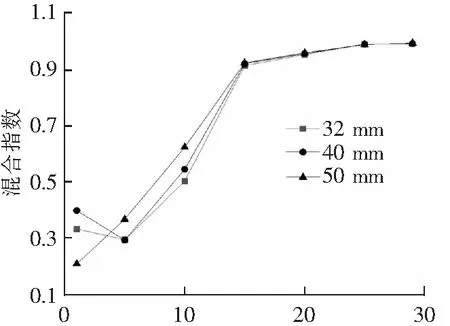
t/s(a) 样本网格大小对混合指数的影响

由图6(a)可知，在0～5 s时，选用不同大小的取样网格，其对应的混合均匀性指数差别明显，这是因为粉体在初始堆积状态下，在两种粉体颗粒的交界面取样时，会认为两种粉体有一定的混合度，因此，在初始阶段，混合均匀性指数越小，越能反映粉体物料混合的真实情况，因此，可以认为，在0～5 s内，选用边长为50 mm的立方体取样更为合理；在5～15 s时，不同时刻混合指数的取值较为接近，在15 s之后，不同时刻混合指数的取值极为接近，综合考虑认为边长50 mm的立方体网格更为合理。由图6(b)可知在0～5 s内，混合均匀性指数较小且会发生波动，这是因为在起始阶段，床层膨胀，整体粉体床层整体向上运动，随着两种粉体分界面向上提升，在虚拟取样网格内会认为粉体进行了一定程度的混合。在5～15 s内，由于喷射区的形成，两种粉体在喷泉区发生剧烈混合，此阶段的混合均匀性指数快速增大。在15 s之后，随着混合过程的进行，两种粉体的混合已经到了较高的水平，混合指数随时间的变化开始变得缓慢。当混合均匀性指数达到0.95时，可以认为两种粉体的混合已经基本均匀，所需要的时间约为20 s，之后随着混合过程的进行，混合指数略微增加，最终可达到0.99以上，认为两种粉体混合均匀。