基于层次分析法的MIG焊焊缝几何形貌监测

马国红，洪蕾，李健,余乐盛,何银水，肖文波

(1.南昌大学a.机电工程学院，江西 南昌 330031；b.江西省轻质高强结构材料重点实验室，江西 南昌 330031；c.资源环境与化工学院，江西 南昌 330031；2.南昌航空大学无损检测技术教育部重点实验室，江西 南昌 330063)

随着工业的快速发展，人们对材料的耐腐蚀性提出了更高的要求。镀锌钢板因其良好的抗腐蚀性和成本效益在汽车、船舶、建筑等行业得到了广泛的应用[1-2]。在焊接的过程中，焊接质量可以通过电弧声、弧光和电流等信号来判断[3]。但是镀锌钢板在焊接时，表面锌蒸发会使焊接过程变得不稳定。干扰噪声会增加焊接信号采集和质量监测的难度[4]。为了避免干扰信号的影响，结构简单、小体积的激光视觉传感器已经在工业中得到了成熟的应用[5]。激光视觉传感技术利用激光三角测量原理测量焊缝尺寸，这比人工手动测量焊缝几何尺寸的精确率更高。激光器在使用时分为斜射型和直射型。当激光照射到母材和焊缝金属表面时，产生代表当下焊缝轮廓的激光条纹。CCD捕获焊缝的激光条纹图像经过一系列的图像处理算法便可以计算焊缝的几何形貌参数[6]。

众所周知，焊接质量受焊接过程中的众多因素影响，且缺少数学方程表达此高度非线性过程[6]。为获得理想的焊缝形貌，焊工会根据经验调整电流、电压、电弧高度、保护气体等参数。这不仅劳动强度大，还受工人情绪的影响。受仿生学中大脑认知机制启发的人工神经网络(artificial neural network,ANN)可以克服这些问题[8]。大量的研究表明ANN有很强的非线性函数逼近能力，可用于拟合多个输入和输出变量之间的关系。如今已研发出的模型多种多样，其中应用最多的包括ART、Radial Basis Function、Hopfield和BPNN。研究表明BPNN已经成功应用在焊接领域的多方面，如焊缝性能预测，接头形状分类，焊接过程控制。Manikya Kanti等[9]提出了BPNN用于预测的焊缝熔深和凸度指数。该模型的输入参数为峰值电流、脉冲频率、送丝速率、送丝速率/焊接速度比和板的厚度。Kim等[10]比较了误差反向传播算法和Levenberg-Marquardt近似算法训练的BPNN模型的训练效果，并根据焊道数、焊接电流、焊接电压和焊接速度这些关键工艺参数预测了焊缝宽度。分析发现BPNN模型具有依靠大规模数据集快速完成精确预测的能力，适用于弧焊的焊缝特征预测。然而，受到不确定环境因素的影响，焊接实验的实际值可能与模型的预测结果存在一定偏差。为了在线调整焊接参数以实现理想的焊缝几何形貌，层次分析法(analytic hierarchy process,AHP)值得一试。AHP于上世纪70年代被美国学者提出，是一种结合定性和定量分析的决策工具。它将决策的问题及其相关影响因素分为多个层次，方法简单，适用于选择最佳方案，资源分配，解决冲突和优化问题[11]。Liu等[12]通过AHP分析了焊缝形貌对接头疲劳性能的影响。Ravisankar等[13]用它决定出熔化极气体保护焊是AA7075高强度铝合金对接焊的最好焊接工艺。李强等[14]则用它来判断工业生产中影响焊缝质量的各因素的重要程度。验证结果都表明AHP决策效果可靠。

文献调查发现，大多数焊接质量的检测方法都只适用于离线，目前没有学者提出结合视觉传感技术与决策经验以实现焊接质量在线监测的方案。本文提出了结合BPNN预测和AHP决策的方法用于镀锌钢板MIG焊焊接质量在线监测。该方法主要由3个阶段组成：阶段一，通过视觉传感和图像处理技术在线提取焊缝的特征参数熔宽和余高；阶段二，利用提取的特征参数与相应的电流、电压和焊接速度构建一个BPNN，该模型用于预测与当前参数设置相对应的几何形貌；阶段三，利用AHP结合经验知识在线决策需要改变的焊接工艺参数，以获得更理想的焊缝。

1 实验系统和参数设置

实验使用的焊接平台包括图像采集系统和MIG焊接系统，如图1所示。图像采集系统主要由工业计算机(IPC)，CCD相机(WAT-902H2)，窄带通滤光片(中心波长为650 nm，带宽为50 nm)，中性减光片(透光率0.1%和50%)，激光传感器(FU655AL30-HGD1465)等硬件和一个VS配置OpenCV开发的软件组成。MIG焊接系统包括弧焊电源(华远NB-350IGBT)、送丝机构(SB-10)、气瓶、焊枪和步进电机。步进电机用来控制焊接方向和焊接速度。

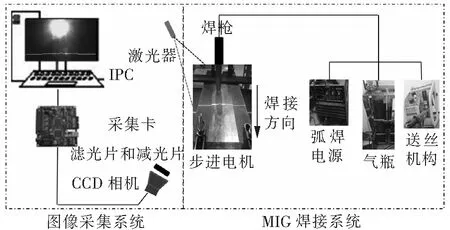
图1 焊接平台Fig.1 Welding platform

本实验使用的搭接材料是尺寸为250 mm×50 mm×1 mm的Q235热浸镀锌钢板。填充材料为直径0.8 mm的低碳钢焊丝。保护气体为质量分数大于99.9%的高纯度氩气，保护气流量为15 L·min-1。其他主要焊接参数如表1所示。

表1 焊接参数Tab.1 Welding parameters

2 激光条纹的预处理与特征点检测

图像处理操作通过MATLAB完成，处理后的激光条纹被用于替代实际的焊缝形貌以进行后续的分析。因此，图像处理算法的准确性、实时性和鲁棒性都非常关键。为了提取激光条纹特征参数，本文提出了一套有效的图像处理算法，如图2所示。具体图像处理算法流程包括激光条纹的提取和特征点的提取两部分。

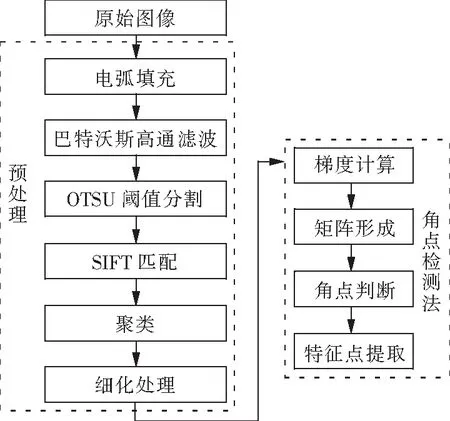
图2 图像处理算法流程图Fig.2 Flow of image processing algorithm

2.1 图像预处理

图3为用CCD相机采集的典型图像，主要包括了弧光区和激光条纹区。激光条纹的轮廓需要经过一系列的图像预处理操作才能得到。图4是激光条纹提取的每个算法步骤的示例图。电弧与激光条纹提取的目的无关，因此需要被去除。roifill函数可填充电弧区域且巴特沃斯高通滤波能有效消除填充边界。填充及滤波后的效果分别如图4(a)、(b)所示。为了完全分离激光条纹与背景，需要对滤波后图像进行阈值处理。经过比较，最终确定使用OTSU算法，处理效果如图4(c)所示。镀锌钢板表面花纹导致材料对激光反射强度不一致，因此激光条纹在阈值处理后轮廓线会不完整。形态学处理可以连接细小的缺口部分，分析表明合适参数选择后的闭运算能取得最好的效果，如图4(d)所示。为了进一步去除图像中的干扰点，运用了尺度不变特征变换(scale invariant feature transform，SIFT)算法和聚类处理。SIFT算法的作用是对干扰和焊后无明显干扰背景下采集并阈值化后图像进行匹配，该算法的结果表现为一定数量的匹配点，如图4(e)所示。随后，这些匹配点可以作为图像聚类的依据，如图4(f)所示。最终，激光条纹被从激烈干涉的背景中准确提取，如图4(g)所示。然而，聚类后的激光条纹仍然相对较粗，无法直接利用它提取所需的特征点。所以必须对激光条纹进行细化，图4(h)是细化处理后的效果。

图3 原始图像Fig.3 Original image

(a) 填充 (b) 滤波 (c) 阈值分割 (d) 闭运算

2.2 特征点检测与特征参数计算

Harris角点检测法[15-17]因算法简单，计算速度快，性能稳定而被广泛应用。它主要包括梯度计算、矩阵形成和角点判断3个步骤。在经过以上图像预处理阶段后，本研究先用Harris角点检测法从细化图像中提取到5个特征点，如图5(a)所示。然后，从左到右用1、2、3、4、5标记这些特征点，如图5(b)所示。焊缝的熔宽(W)和余高(H)可以表示为：

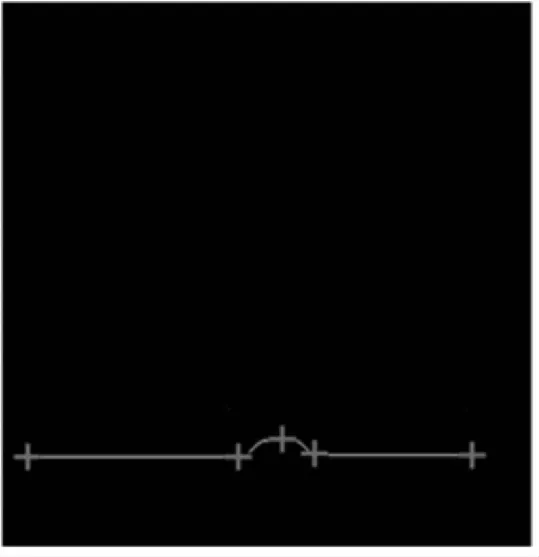
(a) 特征点提取

(1)

(2)

式中:x2、x3、x4分别表示特征点2、3、4的横坐标；y2、y3、y4则是特征点2、3、4的纵坐标。

3 预测与决策

3.1 余高熔宽与电流电压的关系

本研究通过控制变量法进行了MIG焊接实验，建立了焊缝形貌与重要工艺参数之间的定量关系。实验过程中保持其他焊接参数不变，仅改变焊接电流可获得获得电流变化与焊缝余高变化之间的关系，如图6(a)所示。同样仅改变焊接电压，可获得焊接电压变化与焊接熔宽变化之间的关系，如图6(b)所示。数据拟合的结果表明平均每单位电流的变化导致余高改变0.12个像素，而每单位电压的变化导致熔宽改变4.29个像素。

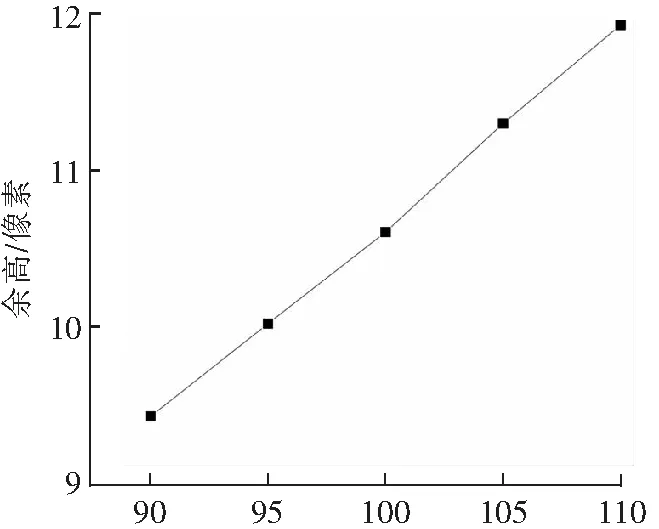
电流/A(a) 焊接电流对余高的影响

3.2 BPNN模型预测

BPNN是一种前馈神经网络，其结构如图7所示。当输出层无法在正向传播中达到预期效果时，则进行误差反向传播。3层BPNN模型的输入参数为焊接电流、焊接电压和焊接速度，因此输入层节点数为3。输出参数为余高和熔宽，因此输出层节点数为2。根据经验公式(3)计算得出该模型的隐藏层节点数在3～12之间。

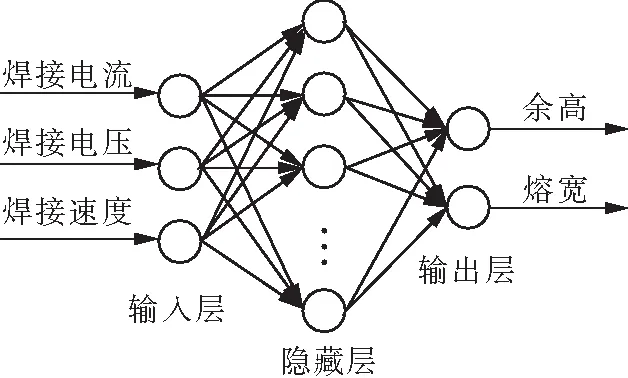
图7 BPNN的结构Fig.7 Structure of BPNN

(3)

式中：h为隐藏层节点数；m为输入层节点数；n为输出层节点数；α为1～10之间的常数。

本研究基于360组实验样本数据完成了BPNN的构建，经过测试证明隐藏层节点数为12时取得最好的拟合精度，高达95.83%。当实验焊缝与模型预测余高差在±0.5像素范围内且熔宽差在±5像素范围内就可以认为焊缝获得了预期的效果。为了验证模型的准确性，一组未用于训练模型的焊接参数电流100 A，电压25 V，焊接速度5.5 mm·s-1被选择进行了焊接测试。图8展示了焊接后获得的焊缝。每间隔1 cm取一个测量点，提取该处激光条纹并计算焊缝高度和焊缝宽度。将所选的12个测量点的平均高度代表整个焊缝的余高，平均宽度代表整个焊缝的熔宽。测量计算的焊缝实际余高和熔宽分别为10.41像素和58.64像素，BPNN模型预测的焊缝余高和熔宽分别为10.72像素和60.87像素。模型预测和实验焊缝的余高差为0.31像素，熔宽差为2.23像素。很显然本组焊接参数获得的实验计算与模型预测值的差值在允许范围之内。

图8 实验焊缝Fig.8 Experimental weld

3.3 AHP模型决策

由于焊接过程受环境等不确定因素影响，实验实际几何形貌值和模型预测值之间的差并不总能在误差范围内。因此，本文设计了基于焊接经验的AHP模型，如图9所示。最高层是决策需要解决的问题，可能是改变熔高也可能是改变熔宽。中间层是决策的准则，由板厚B1、焊接位置B2和焊丝直径B33个因素组成。最底层是决策时备选方案包括调整电流C1、电压C2和焊接速度C3。当实际值与预测值存在较大误差时，模型决定调整焊接参数，让决策目标的实际值和预测值之间的差值减小到允许范围内，以实现理想的焊接效果。

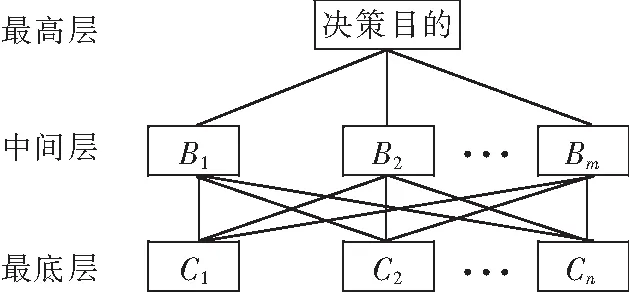
图9 层次分析法决策模型Fig.9 AHP decision model

当焊接电流为76 A，焊接电压为22 V，焊接速度为5.83 mm·s-1时，获得的实验焊缝余高和熔宽分别为8.65像素和45.91像素，如图10中焊缝A所示。而模型预测的焊缝高度和宽度分别为9.22像素、47.34像素。尽管焊缝熔宽的实验值与期望值的误差仅1.43像素，远小于5像素的误差允许范围，余高实验值与期望值误差超出了0.5像素的误差允许范围，为0.57像素。故判断焊缝A超出误差范围。AHP最高层决定改变焊缝余高，从最高层向最底层进行决策，过程如下。

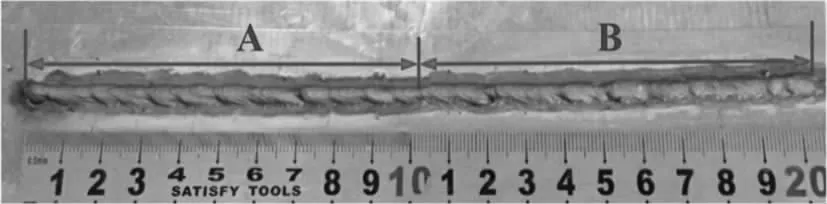
图10 焊缝Fig.10 Weld

1) 最高层的余高支配着中间层的所有因素，获得判断矩阵B：

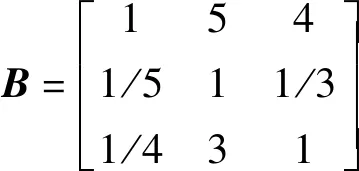
经计算得出一致性指标Q等于0.042 9。三阶矩阵的平均随机性指标I为0.58。因此，一致性比率R等于0.074 0。因为R小于0.1，故判断矩阵B通过了一致性检验。然后权重WB被求出等于[0.673 8,0.100 7,0.225 5]。

2) 中间层所有因素都关联着最底层的所有因素，获得判断矩阵C1、C2和C3：

同样，计算出的R1、R2和R3分别为0.003 1、0.015 7和0.081 0，均小于0.1。故判断矩阵C1、C2和C3均通过一致性检验。最终计算的相应权重W1、W2和W3分别为[0.648 3,0.122 0,0.229 7]、[0.319 6,0.558 4,0.122 0]和[0.186 5,0.687 0,0.126 5]。总一致性比率被计算出来是0.022 3，也小于0.1，故总排序一致性检验通过，总权重为[0.511 1,0.293 3,0.195 6]。各备选方案的权重C1>C2>C3，所以AHP模型最后做出调整焊接电流的决策。

在决策备选方案确定后，AHP触动相应的参数调整过程，将焊接电流增加了4 A。新产生的焊缝实际余高和熔宽分别为9.11像素和46.27像素，如图10中焊缝B所示。余高和熔宽的误差都进一步减小，分别变成了0.11像素和1.07像素。调整参数后的焊缝B较调整参数前的焊缝A实现了预期效果。图11(a)和图11(b)分别展示了焊缝A、B各测量点余高和熔宽的实验值。

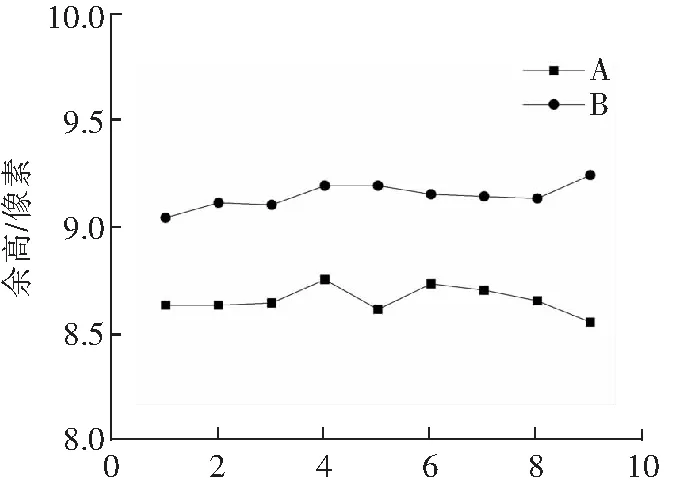
测量点(a) 高度值

4 结论

根据大量的镀锌钢板MIG焊搭接实验数据，建立了焊缝几何形貌特征参数与焊接工艺参数之间的有效BPNN模型，并定量分析了余高与电流、熔宽与电压的关系。提出的AHP模型，可以在BPNN预测值和实际几何形貌特征值的误差过大时，对焊接工艺参数进行决策。实验结果表明，所提出的方法可用于在线调整焊缝几何形貌，进而控制焊接质量。根据这项工作获得的结果，未来可以将其应用到其他焊接方法。另外，图像处理算法的进一步改进将确保更准确和可靠的预测结果。