基于隐马尔可夫链的自适应MODE及应用

崔彩霞，毕超超，范勤勤，3

1.上海海事大学 物流科学与工程研究院，上海201306

2.上海海事大学 物流研究中心，上海201306

3.上海交通大学 电子信息与电气工程学院，上海200240

差分进化算法[1]是由Storn和Price于1997年提出的一种高效元启发式搜索算法。由于该算法易于实现、寻优性能强、鲁棒性好，从而吸引了国内外学者的关注与研究，并被用于求解各领域的优化问题。

除求解单目标优化问题外，差分进化算法也被用来求解各类多目标优化问题。为提高其性能，各种多目标差分进化算法（Multi-Objective Differential Evolution Algorithm，MODE）被不断提出。比如Kukkonen 等人[2]于2005 年提出的GDE3（The Third Evolution Step of Generalized Differential Evolution）算法是其中一种较为典型的多目标差分进化算法，并被用于解决有约束的多目标优化问题。该算法对变异策略进行改进，并且增加新的选择规则。张春美等人[3]提出一种参数自适应的分布式差分进化算法（Distributed Differential Evolution Algorithm with Adaptive Parameters，APDDE）。该算法根据冯·诺依曼拓扑结构将初始种群分为多个子种群，用子种群的优秀个体代替其邻域子种群中的较差个体，并根据个体适应值的变化情况对种群内各个体分配不同的F和CR，从而实现参数自适应。结果表明该算法在收敛速度和求解质量上都有所提高。李牧东等人[4]于2016年提出一种基于最优高斯随机游走和个体筛选策略的差分进化算法（Differential Evolution Based on Optimal Gaussian Random Walk and Individual Selection Strategies）。在该算法中，首先利用最优高斯随机游走策略产生新的种群；然后仅对种群中性能较差的个体进行交叉和变异操作，并使用改进的个体筛选策略来产生新个体；最后，得到一个新种群。实验结果表明该算法具有较快的收敛速度和较好的鲁棒性。Fan 等人[5]提出一种基于性能指标的多目标差分进化算法（Multi-Objective Differential Evolution with Performance-Metricbased Self-adaptive Mutation Operator，MODE-PMSMO）。该算法采用一种多目标性能评价指标来指导变异策略的动态调整。所得结果表明MODE-PMSMO 能够根据进化进程自适应得到合适的变异策略来求解相应类型的多目标优化问题。候莹等人[6]提出了一种基于参数动态调整的多目标差分进化算法（Adaptive Multi-Objective Differential Evolution Algorithm Based on the Dynamic Parameters Adjustment，AMODE）。该算法通过实现控制参数自适应的方式来提高其求解多目标优化问题的能力。实验结果表明该算法能够有效提高所得帕累托前沿的收敛性和多样性。Lin等人[7]于2018年提出一种具有多种差分进化策略的自适应免疫启发多目标算法（An Adaptive Immune-inspired Multi-Objective Algorithm with Multiple Differential Evolution Strategies）。该算法将差分变异算子融入到多目标免疫算法中，结果表明所提算法有效提高了解集的多样性。艾兵等人[8]提出一种基于多策略和排序变异的多目标差分进化算法（Multi-Objective Differential Evolution Algorithm with Multi-strategy and Ranking-based Mutation，MODEMERM）。该算法利用基于多策略和排序变异的DE 算子进行变异操作。所得结果表明MODE-MERM采用多种变异策略能够平衡解集的收敛性与多样性。童旅杨等人[9]于2019 年提出一种基于分解和多策略变异的多目标差分进化算法（Multi-Objective Differential Evolution Algorithm Based on Decomposition and Multi-Strategy Mutation，MODE/DMSM）。该算法利用改进的切比雪夫分解方法将多目标优化问题分解成多个单目标子问题；并采用多策略变异的方法来求解各个子问题。实验结果表明MODE/DMSM使用多个差分变异算子能够得到多样性和收敛性较好的解集。

虽然众多学者对多目标差分进化算法已进行大量研究，但是在其控制参数和策略自适应方面仍存在一些问题。比如，现有多目标差分进化算法的自适应方法一般不具有预测功能，因此这会大大降低其所得控制参数和策略的适应性。为解决该问题，本研究提出一种基于隐马尔可夫链的自适应多目标差分进化算法（Selfadaptive Multi-Objective Differential Evolution Algorithm Based on Hidden Markov Chain，SMODE-HMC）。在SMODE-HMC 算法中，隐马尔可夫链方法被分别用来预测控制参数和变异策略的演化趋势，从而实现自适应调整。通过16 个基准多目标优化问题的测试，结果表明所提算法的整体性能要好于其他9 种比较算法。另外，本研究还将SMODE-HMC 算法用于求解海铁联运多目标优化问题，得到令人满意的结果。

1 预备知识

1.1 多目标优化问题

在现实世界中，多目标优化问题（Multi-objective Optimization Problems，MOPs）广泛存在于各个领域，如多目标柔性车间作业调度[10]、电动车充电站规划[11]等问题。通常情况下，多目标优化问题中的各个子目标相互矛盾且不可调和。不失一般性，多目标优化问题的数学形式表示如下：

其中，x为决策向量；Ω∈RD为D维决策空间；m表示优化目标数量。其他一些相关概念如下：

定理1（支配关系）向量p支配另一个向量q（记作p≻q）的条件是：如果对∀w∈{1,2,…,k},pw≤qw，并且p≠q。

定理2（Pareto 最优解集）一个向量x*∈Ω，如果不存在其他向量x∈Ω，使得F(x)≻F(x*)，那么就称x*为Pareto解，x*的集合（记作X*）被称为Pareto最优解集。

定理3（Pareto 前沿）多目标优化问题中，Pareto 最优解集中的解对应的目标向量被称为Pareto前沿（Pareto Front，PF）。

1.2 多目标性能评价指标

多目标性能评价指标能够对所得解集质量做出评判，通常使用的方法有世代距离（Generational Distance，GD）、空间分布评价方法（Spacing，SP）与反向世代距离（Inverted Generational Distance，IGD）[12-14]。其中GD是收敛性指标，评价的是所得解集与真实Pareto前沿的逼近程度；SP 是多样性指标，评价的是所得解集在真实Pareto前沿上分布的均匀性；IGD是综合性指标，评价的是所得解集的收敛性和多样性。具体计算公式如下：

（1）GD

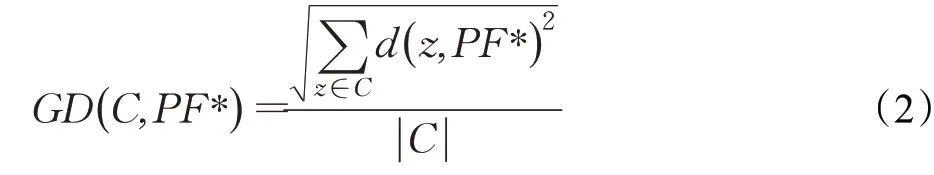
式中，PF*表示一组沿着真实PF均匀分布的解集；C表示算法得到的PF逼近；d(z,PF*)表示z与PF*最近点的欧几里德距离；|C|表示C中解的数量。GD 值越小，说明所得解集的收敛性越好，与PF越逼近。

（2）SP

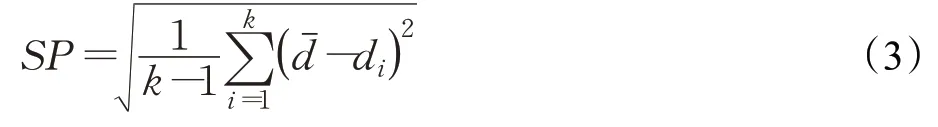
式中，k表示非支配解的个数；di表示第i个解与其他解的最小欧几里德距离；dˉ表示所有di的平均值。SP值越小，说明所得解集的均匀性越好。值得注意的是该性能指标并未对所得解集的延展性进行评价。

（3）IGD

式中，d(z*,C)表示z*与C最近点的欧几里德距离；|PF*|表示PF*中解的数量。IGD值越小，说明所得目标解集的收敛性和多样性就越好。

1.3 标准差分进化算法

差分进化算法是一种高效的元启发式搜索算法，标准差分进化算法主要有以下几个步骤：

（1）初始化

设置参数，例如初始化缩放因子F、交叉概率CR、种群规模PS和最大迭代次数等。同时，在定义域(Ω)内，生成初始化种群。

（2）变异

种群中的个体通过变异策略生成变异个体，差分进化算法常用的变异策略如下所示：

式中，D为多目标优化问题的维度，Rj为[0，1]之间均匀随机数，jrand为[1,D] 范围内的一个随机整数。

（4）选择

选择试验个体与种群个体中较优个体进入下一代，选择方式如下：

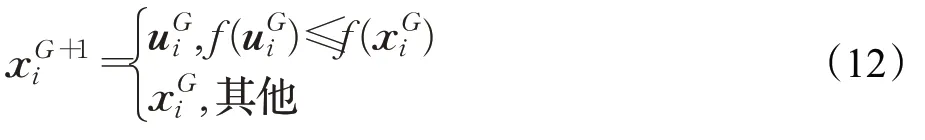
1.4 隐马尔可夫模型

隐马尔可夫模型（Hidden Markov Model，HMM）是马尔可夫链（Markov Chains，MC）的其中一种方法。在隐马尔可夫模型中，最难确定的是隐含状态参数。虽然HMM的隐藏状态不能被直接观测到，但是隐藏状态会通过一定的概率分布在外部状态中被观测到。因此，隐马尔可夫模型是一个隐藏和非隐藏的双重随机过程，第一重是一个隐藏状态转移到另一个隐藏状态的随机过程，这是不可被观测的；第二重是一个隐藏状态到外部展现的随机过程，这是可以被观测的。隐马尔可夫模型的一些相关概念如下[15]。

隐马尔可夫模型的图结构如图1 所示。其中{s1,s2,…,sN}是HMM 的状态序列，即隐藏的马尔可夫链。其中st∈S表示t时刻模型的状态。S={g1,g2,…}表示有K1个可能取值的状态空间；{o1,o2,…,oN}是HMM 的观测序列，其中ot∈O表示t时刻模型的观测值。{h1,h2,…} 表示O的取值范围。

图1 隐马尔可夫模型

在HMM中，各个隐藏状态间的转换概率称为状态转移概率，通常记为矩阵，其中：

模型在初始状时刻各状态出现的概率即为初始状态概率，记为π={π1,π2,…}，且=1。

综上，HMM可用其参数λ={A,B,π} 来指代。

2 基于隐马尔可夫链的自适应多目标差分进化算法

研究表明隐马尔可夫模型具有良好的预测能力[16]。因此，为提高多目标差分进化算法的性能，提出一种基于隐马尔可夫链的自适应多目标差分进化算法。在该算法中，将父代种群、变异种群和交叉种群转换为概率作为隐马尔可夫模型中的参数，并通过计算最大似然估计值实现对控制参数的自适应更新；另外，通过改进的IGD指标不断更新隐马尔可夫模型中的参数，从而不断更新通过隐马尔可夫模型生成的策略链，实现变异策略选择的自适应；而且为保证算法前期偏向于全局搜索和后期偏向于局部搜索，本文采取多项式交叉和模拟二进制交叉的混合交叉策略。隐马尔可夫模型所需参数的初始值均设置为等概率。控制参数自适应与变异策略自适应的具体实现方式见以下部分。

2.1 控制参数自适应

进化过程中，种群随迭代次数的变化情况与隐马尔可夫模型内部过程类似[16]。在该部分，将个体的状态变化情况分为三种：优、中、差。优表示当前个体支配比较个体，中表示当前个体与比较个体互不支配，差表示比较个体支配当前个体。

在每一次迭代过程中，种群中每个个体都有与其相对应的变异缩放因子与交叉概率。对比个体的实际状态序列与最优隐藏序列得到相应行向量，然后计算行向量的最大似然估计值来得到个体对应的F与CR。控制参数自适应方法的具体步骤如下：

步骤1 初始化状态转移矩阵A。设置三种状态之间的转移是等概率的，即A=[1/3,1/3,1/3;1/3,1/3,1/3;1/3,1/3,1/3]。

步骤2 得到混淆概率矩阵B。将父代种群、变异种群和交叉种群转换为概率，作为隐马尔可夫模型中的混淆概率，转换方法详见算法1（参考文献[16]）。对种群中每个个体而言，其对应的混淆概率矩阵B的大小为3×D。

步骤3 得到实际状态序列。个体状态可以利用隐马尔可夫模型中的概率矩阵来评估[16]。在本文中，设置0～1/3 代表“差”状态，1/3～2/3 代表“中”状态，2/3～1 代表“优”状态。从而可得到每个个体变异之后的实际状态序列realMutseq、交叉之后的实际状态序列realCanseq，序列大小都为1×D。

步骤4 得到最优隐藏序列。父代种群观察到的父代观测序列记为EMseq，变异种群观察到的变异观测序列记为Mutseq，交叉种群观察到的交叉观测序列记为Canseq。每个个体对应观测序列大小都为1×D。利用隐马尔可夫模型中的Viterbi 算法[17]分别求出父代个体观测序列与变异个体观测序列条件下的最优隐藏序列，记为bestMutseq和bestCanseq。

步骤5 变异缩放因子F与交叉概率CR的计算方式如下：

对种群中的每个个体，对比其实际状态序列real-Mutseq与最优隐藏序列bestMutseq中每一列的值，若相等，将1 存入行向量lm中对应列位置，否则存入0。同理对比realCanseq与bestCanseq，得到行向量lc。

式中，MLE(⋅)表示最大似然估计值。

种群信息转换为概率的伪代码如算法1所示。

算法1 种群信息转换为概率

输入：种群大小为PS×D的种群pop。

（1）建立一个大小为PS×D的新矩阵popr；

（2）建立两个长度为D的向量δ和ε；

（3）计算种群pop中每一列的平均值与方差，分别计入δ和ε；

（4）计算种群pop中每一行i和每一列j即pop(i,j)的概率分布，计入popr(i,j)。

输出：popr。

2.2 变异策略自适应

为实现多目标差分进化算法变异策略自适应，本研究采用改进的反向世代距离对变异策略进行评价，再使用隐马尔可夫链模型对变异策略进行预测生成。本研究使用“DE/rand/1”“DE/best/1”和“DE/current-to-best/1”三种变异策略。即，隐马尔可夫模型中的三种隐藏状态可以表示如下：策略1、策略2、策略3，其中策略1 表示“DE/rand/1”，策略2 表示“DE/best/1”，策略3 表示“DE/current-to-best/1”。前者有很好的全局开发能力，后两者有较好的局部探索能力，能够保持全局搜索与局部搜索的平衡。

设置隐马尔可夫模型中有三种观测状态：优、中、差。优表示当前变异个体支配对应父代个体；中表示当前变异个体与对应父代个体互不支配；差表示对应父代个体支配当前变异个体。

初始化阶段，设置三种状态之间的转移是等概率的以及在某一状态下观测到各策略的概率是相等的。即变异差分策略的状态转移概率矩阵A与混淆概率矩阵B均为[1/3，1/3，1/3；1/3，1/3，1/3；1/3，1/3，1/3]，通过隐马尔可夫模型生成一个选择变异策略的初始策略链，记为chain，大小为1×PS。变异策略自适应方法的具体步骤如下：

步骤1 根据个体选择变异策略的不同，将种群划分为三个子种群，分别记为Prand、Pbest、Pcurrent，对应的目标空间解集记为Crand、Cbest、Ccurrent，它们对应的改进反向世代距离分别记为mIGDrand、mIGDbest、mIGDcurrent。改进反向世代距离计算公式如下：

步骤2 各个策略所得改进反向世代距离值越小，说明选择该策略的变异效果越好。因此，状态转移矩阵设置为：

步骤3 同理，各个策略的改进反向世代距离值越小，说明在该策略状态下，观测到“优”的概率较大。因此，混淆矩阵表示如下：

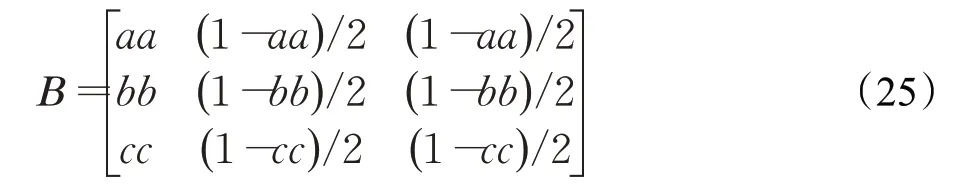
步骤4 利用矩阵A和B作为隐马尔可夫模型参数生成一个新的策略链chain。

2.3 混合交叉策略

为保证算法前期有较好的全局搜索能力和后期有较好的局部搜索能力，本研究采取一种多项式交叉和模拟二进制交叉混合使用的交叉策略。其中，模拟二进制交叉（Simulated Binary Crossover，SBX）具有很强的局部搜索能力[18]；而多项式交叉则有较好的全局搜索能力。因此，本文设置一个随迭代次数不断变小的μ来达到此目的[19]。

从公式（26）可以看出，μ在种群进化前期具有较大值，故选择多项式交叉的概率较大，此时算法偏向于全局搜索；算法后期，μ值减小，选择SBX 交叉策略的概率较大，算法偏向于局部搜索。

2.4 SMODE-HMC算法的基本流程

步骤1 设置参数PS、F、CR、最大迭代次数等，并利用隐马尔可夫模型生成初始策略链chain。

步骤2 如果G<0.2×Gmax[5]，所提算法只使用“DE/rand/1”变异策略，否则使用2.2 节来自动选择合适的变异策略。确定策略后，依据2.1 节计算F的数值，然后进行变异操作。

步骤3 依据2.1 节计算CR的数值。若rand<μ，选择多项式交叉策略，否则使用模拟二进制交叉策略。

步骤4 对试验个体进行边界值判定[5]；如果一个随机数rand>Bset[20]那么

式中，Lj和Uj表示变量第j维的下界与上界。否则在定义域(Ω)范围内重新生成新的试验个体。

步骤5 环境选择。若是三目标问题，采用文献[21]中的tDEA方法；若是双目标问题，则采用快速非支配选择方式[22]。

步骤6G=G+1。

步骤7 循环步骤2到步骤6，直到满足最大迭代次数。

3 实验结果与分析

为验证SMODE-HMC算法的性能，将其与另外9种多目标进化算法在9个三目标（WFG1～WFG9）和7个双目标（UF1～UF7）测试函数上进行性能对比。其他9 种多目标进化算法分别为MOEAD[23]、NSGAIII[24]、GDE3[2]、ARMOEA[25]、LMEA[26]、MOEADDE[27]、tDEA[21]、MMOPSO[28]、MODE-SS[19]，其中前8 种算法的结果由文献[29]提供的软件求得。为保证实验结果分析的可靠性，采用Wilcoxon 和Friedman 非参数检验方法对实验结果进行统计分析，显著性水平设置为5%。其中“+”“－”分别表示所提算法优于、劣于相比较算法；“≈”表示所提算法与相比较的算法性能相近。

3.1 参数设置

在本研究中，所有测试函数的种群数量均设置为120，三目标的最大迭代次数设置为300，双目标的最大迭代次数设置为200，每一种算法求解每一个测试函数均独立运行20次。比较算法的参数设定均与原始文献一致。

3.2 算法比较

SMODE-HMC 与其他9 种比较算法得到的GD 平均值与方差以及Wilcoxon 统计结果见表1。从表1 可以看出，SMODE-HMC 分别优于MOEAD、NSGAIII、GDE3、ARMOEA、LMEA、MOEADDE、tDEA、MMOPSO、MODE-SS 算法12、10、14、10、11、11、9、13、14 个测试函数，分别劣于以上算法3、3、1、2、3、2、2、1、1 个测试函数，另外分别有1、3、1、4、2、3、5、2、1个测试函数与以上相比较的算法性能相近。同时，10 种算法得到GD 的Friedman 统计分析结果见表2，实验结果显示SMODEHMC 排名第一，说明本文所提算法得到的Pareto 前沿与真实PF最为接近，收敛性是所有算法中最好的。其主要原因是SMODE-HMC算法使用了自适应变异策略和混合交叉策略，它能够根据不同类型的多目标优化问题来选择合适的生成策略。同时，控制参数自适应策略为算法提供合适的参数使其适应不同的进化阶段或问题。

表1 所有比较多目标进化算法得到的GD平均值与方差

表2 所有比较算法在GD平均值上的性能排序

SMODE-HMC与其他9种比较算法得到的SP平均值与方差以及Wilcoxon统计结果见表3。从表3可以看出，MOEAD、NSGAIII、GDE3、ARMOEA、MODESS 等算法在3个测试函数上优于所提算法；tDEA和MMOPSO算法在2个测试函数上优于所提算法；而MOEADDE只在1 个测试函数上比所提算法性能好。除了LMEA，SMODE-HMC 的整体性能优于其他8 种比较算法。LMEA在大部分三目标测试函数上的SP值要小于所提算法，这是因为LMEA算法利用聚类方法将决策变量分为两组，其中一组特意考虑了多样性指标。但是，从整体性能来看（见表4），所提算法在性能指标SP上的表现要比LMEA略好。其主要原因是SMODE-HMC算法利用隐马尔可夫模型分别来预测控制参数和变异策略，使其在进化过程中自适应调整。

表3 所有比较多目标进化算法得到的SP平均值与方差

表4 所有比较算法在SP平均值上的性能排序

SMODE-HMC 与其他9 种比较算法得到的IGD 平均值与方差以及Wilcoxon统计结果见表5。从表5可以看出，SMODE-HMC分别优于MOEAD、NSGAIII、GDE3、ARMOEA、LMEA、MOEADDE、tDEA、MMOPSO、MODESS 算法15、7、12、8、11、11、7、9、10 个测试函数，分别劣于以上相比较算法1、4、3、4、4、4、3、6、1个测试函数，另外分别有0、5、1、4、1、1、6、1、5 个测试函数与以上相比较的算法性能相近。同时，10种算法得到IGD的Friedman统计结果见表6，实验结果显示本文所提算法SMODEHMC排名第一，说明SMODE-HMC算法得到的解集整体分布性最好。其主要原因是SMODE-HMC算法在进化过程中能够自动选择合适的变异策略，并生成合适的控制参数来提高其求解不同类型多目标优化问题的能力。

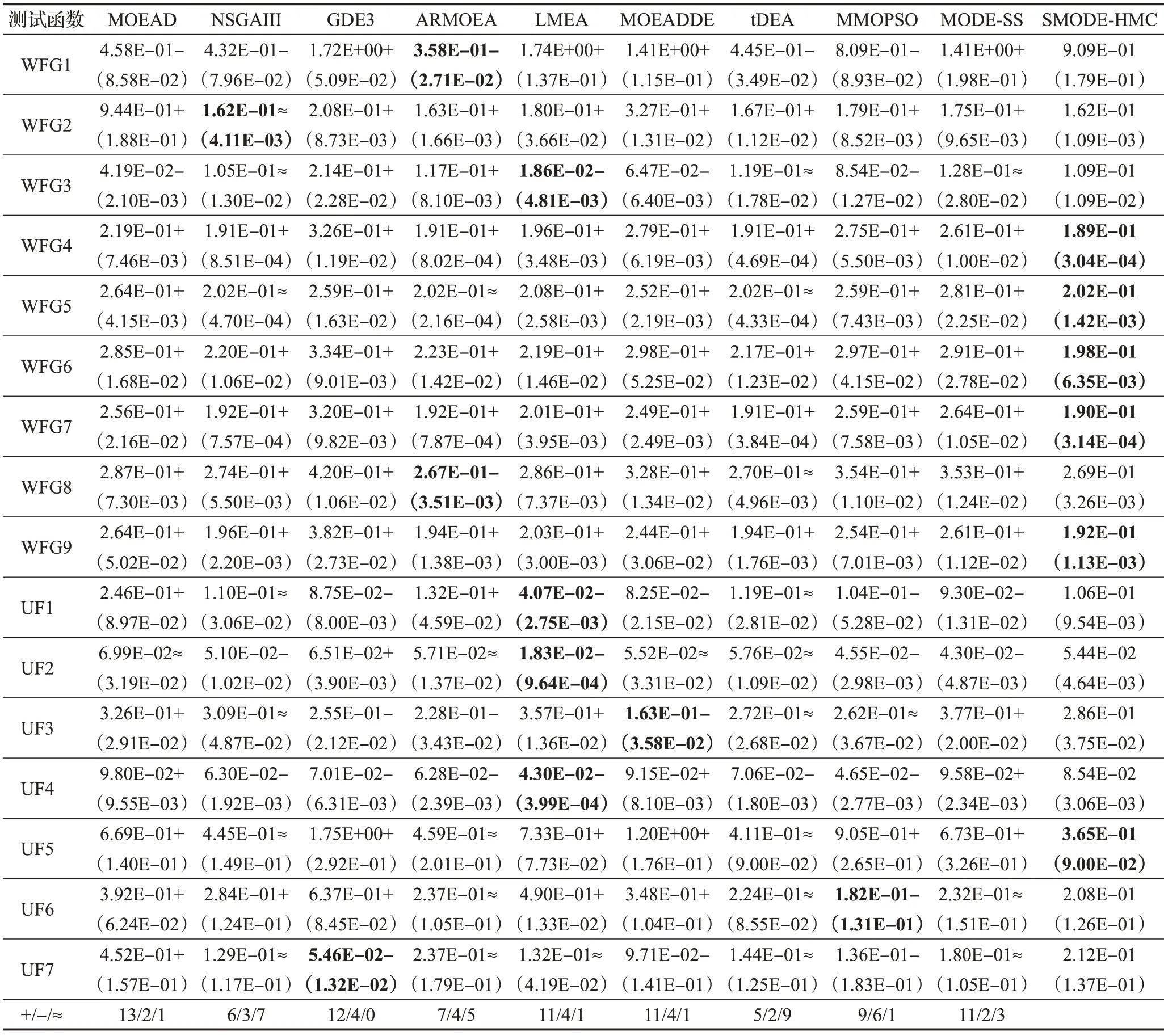
表5 所有比较多目标进化算法的IGD平均值与方差

表6 所有比较算法在IGD平均值上的性能排序

综上，SMODE-HMC 算法所得解集的收敛性和多样性是所有比较算法中最好的。

3.3 算法分析

由以上实验结果可知，SMODE-HMC 在16 个多目标测试函数上的整体表现优于其他9 种多目标进化算法。其主要原因是控制参数和策略自适应方法能够为多目标差分进化算法提供实时有效的控制参数和策略。本节将对所提算法控制参数和变异策略在进化过程中的自适应性进行分析。

3.3.1 控制参数自适应分析

本实验给出SMODE-HMC在两个测试函数（WFG5、UF3）上控制参数F与CR平均值的进化曲线（见图2）。

从图2（a）中可以看出，控制参数F与CR的整体变化趋势类似，前期逐渐减小，后期又随着迭代次数的增加而缓慢增大。图2（b）中，F与CR的整体变化趋势也类似，先增加后减小。

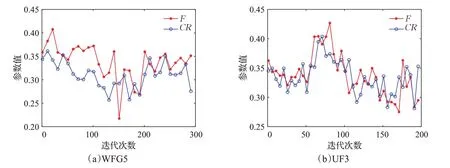
图2 SMODE-HMC控制参数F 和CR 的进化曲线

由上可知，SMODE-HMC 算法的控制参数根据不同类型的多目标优化问题而实现自适应实时调整。

为进一步验证所提方法的有效性，在实验中使用固定控制参数的SMODE-HMC（命名为SMODE-HMC-1）；并用WFG5 和UF3 两个测试函数来进行测试。所得到的GD、SP与IGD值见表7。

从表7可以看出，SMODE-HMC-1在两个测试函数上的表现均劣于SMODE-HMC。这表明，相比于固定的参数设定策略，控制参数自适应策略能够提高多目标进化算法的求解性能。

表7 SMODE-HMC和没有参数自适应SMODE-HMC所得结果

综上，本研究使用隐马尔可夫模型来实现多目标进化算法的控制参数自适应是有效和可行的。

3.3.2 变异策略自适应分析

本部分将使用两个测试函数WFG5和UF3对SMODEHMC 算法变异策略的自适应进行分析。需要注意的是，当G≥0.2×Gmax时，SMODE-HMC才使用变异策略自适应策略；在此之前，算法只使用DE/rand/1 变异策略。这主要是让所提算法在进化前期有足够的全局探索能力。各个变异策略在整个进化过程中的数量和占比分别见图3和图4。

从图3（a）中可以看出，SMODE-HMC 在前期主要使用DE/rand/1 和DE/best/1 两个变异策略；中期使用DE/curret-to-best/1 较多；进化后期策略DE/curret-tobest/1 和DE/best/1 作用类似。图3（b）显示，变异策略DE/rand/1 在整个进化过程中几乎都占据主导位置，而变异策略DE/curret-to-best/1 和DE/best/1 在整个进化过程中的作用似乎差不多。从上可得，SMODE-HMC 可以根据不同类型的多目标优化问题实时选择合适的变异策略，因此，该自适应变异策略可以大大提高搜索性能。另外，三种变异策略在整个种群进化过程中的占比见图4。从图4可知，变异策略DE/rand/1被使用的次数最多。其主要原因是，对于复杂问题，算法只有拥有良好的全局搜索能力，才能找到高质量的解。同时，变异策略DE/curret-to-best/1 和DE/best/1 在这两个测试函数上被使用的频率几乎相同。但根据图3所得，它们在不同的进化阶段发挥不同的作用。

图3 SMODE-HMC变异策略的进化曲线

图4 SMODE-HMC求解测试函数时三种变异策略数量占比

为进一步验证策略自适应的有效性，本实验使用固定变异策略的SMODE-HMC 来求解WFG5 和UF3。由图4 可知，DE/rand/1 在三种变异策略中使用次数最多，故SMODE-HMC只使用它来对个体进行变异操作，算法命名为SMODE-HMC-2。所得GD、SP与IGD值见表8。

表8 SMODE-HMC和没有策略自适应SMODE-HMC所得结果

从表8可以看出，SMODE-HMC-2在两个测试函数上的性能评价指标值均劣于SMODE-HMC，说明变异策略自适应能够使多目标差分进化算法的性能更好。

综上，隐马尔可夫链可以辅助SMODE-HMC 算法实现变异策略的自适应选择，从而提高其求解多目标优化问题的能力。

3.3.3 参数分析

在本实验中，对混合交叉策略中的参数μ进行分析。利用上述16 个测试函数对不同的μ进行测试。图5 表示由Friedman统计分析得到的不同μ值下GD、SP、IGD性能排序平均值。由图5可知，当μ=1-G/Gmax时，算法整体性能最好。故在所提算法SMODE-HMC 中，μ值取μ=1-G/Gmax。

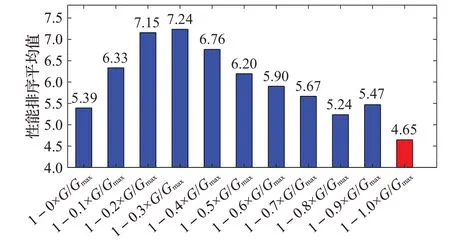
图5 不同μ 值的性能排序

4 SMODE-HMC 在海铁联运能耗优化问题中的应用

在该部分，将SMODE-HMC与上述相比较的9种算法用于求解海铁联运能耗优化问题，以验证SMODEHMC 求解实际优化问题的有效性。种群规模设定为120，最大迭代次数设置为200。能量损耗E与运输时间T的双目标优化建立如下：

式中，f1(v)=E,f2(v)=T,v表示火车或船的速度。海铁联运模拟运输路线、速度与能耗关系详见参考文献[19]。参数PF是将10种算法所得解集进行合并，并挑选其中的非支配解所得到。

10种算法求解海铁联运模型得到的GD、SP与IGD值见表9。从表9 可以看出，本文所提算法SMODEHMC 在GD、SP 和IGD 值上均优于9 种比较算法，说明SMODE-HMC 具有较好的收敛性和多样性，整体性能最好。另外，10种算法求解海铁联运能耗优化问题所得PF见图6。从图6 中也可以看出，SMODE-HMC 所得PF的整体分布要优于所比较的9种算法。

表9 各个算法得到的GD、SP与IGD值

从SMODE-HMC的求解结果中分别选取耗能最大的点Q1 和耗时最长的点Q2，Q1 与Q2 点见图6（a）中绿色实心圆。Q1 与Q2 点火车与船舶在各路段的行驶速度见表10。从表10可以看出速度对耗能与时间皆有影响，显然速度与耗能成正比，与时间成反比。即耗能最大时，各路段行驶速度相对较大；当时间最大时，各路段行驶速度相对较小。特别是在铁路运输上，二者速度的变化率最大。

图6 SMODE-HMC与其他9种算法所得PF 逼近

表10 Q1 与Q2 在各路段的速度

5 结语

差分进化算法的控制参数和生成策略选择对其性能有着显著影响。为提高多目标差分进化算法求解多目标优化问题的能力，本文提出了一种基于隐马尔可夫链的自适应多目标差分进化算法（Self-adaptive Multi-Objective Differential Evolution Algorithm Based on Hidden Markov Chain，SMODE-HMC）。在该算法中，利用隐马尔可夫模型对多目标差分进化算法的控制参数和变异策略进行自适应动态调整；并使用两种不同搜索性能的交叉变异策略来实现算法在进化前期进行全局搜索和进化中后期进行局部搜索。通过与其他9 种多目标进化算法测试对比，实验结果显示SMODEHMC 的整体性能要优于所比较的其他算法。最后，将SMODE-HMC 用于求解海铁联运能耗优化问题，依据所得实验结果分析得出能耗E和时间T与行驶速度的关系，从而为决策者提供重要的决策参考。实验表明SMODE-HMC算法可以为实际多目标优化问题的求解提供有效帮助。