谱聚类算法研究综述
2021-07-28孔钰婷张正航邵金鑫钱育蓉
白 璐,赵 鑫,孔钰婷,张正航,邵金鑫,钱育蓉
1.新疆大学 软件学院,乌鲁木齐830046
2.新疆大学 软件学院重点实验室,乌鲁木齐830046
3.新疆维吾尔自治区信号检测与处理重点实验室,乌鲁木齐830046
聚类分析是一种挖掘数据深层信息与知识的有效方法,聚类是将给定的样本划分成多个簇的过程。聚类最优准则[1-2]的目标是使同一簇内的样本间相似度高,不同簇样本间相似度低。K-均值(K-means)算法是传统聚类中的经典算法,K-means算法虽然易于理解但仍存在局限性,如对样本形状包容性差、易陷入局部最优解[3]等问题。
为能在任意形状的样本空间上达到良好聚类性能,研究者们提出谱聚类算法(Spectral Clustering Algorithm,SC),SC 算法拥有对样本形状敏感度低、收敛于全局最优解、对高维数据支持较好[4]等特点,因此SC算法[5]如今广泛应用于数据挖掘[6]、图像分割[7-9]、模式识别[10]以及遥感[11-12]等领域。近年来随着应用场景变化,大规模数据聚类高时耗问题成为一个研究热点,而谱聚类算法存在同样的聚类挑战[13]。
谱聚类算法是一种建立在谱图理论上的聚类算法,主要分为两类:迭代谱聚类算法与多路谱聚类算法,分别以SM[14]算法与NJW[15]算法为代表。在多路谱聚算法中,为解决NJW算法需要人工设置簇数K等参数问题,孔万增等人[16]利用本征间隙特征,实现自动确定K值的谱聚类算法;为达到更好的聚类性能,王玲等人[17]提出基于数据先验信息的半监督谱聚类算法;为解决谱聚类算高法时空复杂度、对大数据样本适应性差等问题,将谱聚类部署在Hadoop、Spark 等平台,利用平台分布并行特性降低谱聚类算法时耗,或通过优化谱聚类切割模型,来降低算法时间复杂度。
1 谱聚类算法概述
谱聚类算法的思想起源于谱图划分理论[18],谱聚类通过样本相似度生成无向加权图,样本点可看作图的顶点,样本点间的相似度为两点间边的权重,而对无向加权图进行谱图划分就是将图划分为若干个子图,该过程与聚类算法的聚类过程对应。图论的最优划分准则[14]与聚类最优准则在思想上具有一致性,为聚类问题转化为图划分问题提供思路与理论支撑。对于谱图划分而言,图划分准则的选取将直接影响划分结果,常用的图划分准则有规范割集、最小割集、平均割集、比例割集等准则[19]。与谱图划分相比,谱聚类算法考虑问题连续放松形式,将图分割问题转换为求相似矩阵的谱分解问题[20]。谱聚类算法依据划分准则的不同,总体分为迭代谱聚算法与多路谱聚类算法。目前多路谱聚类算法因其简单易于理解特性应用更为广泛,NJW 算法是经典多路谱聚类算法。多路谱聚算法实现细节略有差异,但核心思想基本一致,其主要思想如下:
步骤1 通过样本构建可描述样本特性的矩阵W。
步骤2 计算矩阵W的特征值及特征向量并对其进行排序。
步骤3 取排序后前k个特征值对应特征向量,将向量按列方向排列,组成新解空间。
步骤4 在新解空间上采用典聚类算法进行聚类(模糊聚类、K-means等),最终将聚类结果映射回原解空间。
在谱聚类算法步骤1 中,采用相似矩W来表示样本数据间的相似性是对数据集的特征的一种抽象表达。
1.1 相似矩阵与拉普拉斯矩阵
一般情况下,求解谱图划分的最优划分准则是NP难度问题,通过连续放松形式将图划分问题转化为相似矩阵谱分解问题,因此谱聚类算法是对最优图划分准则的逼近[21]。近年放松形式的谱聚类算法研究较多,最早谱聚类采用样本邻接矩阵直接进行图划分[22],但谱聚类算法的准确率受矩阵质量影响,一般而言矩阵质量越高,聚类结果越理想。
现阶段谱聚类算法多基于相似矩阵(Affinity Matrix),采用W或A表示,本文统一采用W表示。相似矩阵定义如下:

公式(1)中v为数据样本点;d(vi,vj)为两样本点之间的距离,一般取欧氏距离;σ为尺度参数,W随着σ取值变化而改变,因此σ需要经过多次取值实验才能确定[23]。
度矩阵是记为D的对角矩阵,度值为对角元素。计算方式如公式(2)所示:

规范相似矩阵一般形式定义为:

在面向降低W计算量方面,对数据提前进行特定清洗,在去除噪声的同时保留更有代表性的数据;而在提升W质量方面,通过改进相似矩阵的求解的模型或引入监督机制[24],更正相似矩阵,从而提升谱聚类算法聚类性能。
谱聚类算法早期直接采用W的最大k个特征向量进行聚类,但W无法保证被选中的k个特征值对应的特征向量为异块向量。因此,通过W选取特征向量,存在多次选取一块特征向量问题,进而导致选取的特征向量代表性较差。拉普拉斯矩阵L(Laplacian Matrix)为半正定矩阵,L特征值最小为0且对应的特征向量为1。当选取L的前k个特征值所对应的特征向量时,可确保每个分量仅含有一个特征向量[5],因此将L矩阵引入谱聚类中。L矩阵一般分为规范拉普拉斯矩阵和非规范拉普拉斯矩阵,非规范拉普拉斯矩阵表示为:

规范拉普拉斯矩阵两种形式,I为单位矩阵。

1.2 特征值选取
谱聚类算法通常选取前k个特征值所对应的特征向量,以NJW 算法为例,NJW 算法采用公式(3)计算Wnor。而由公式(6)可知,求解Wnor的最大特征值等同于求解Lnor的最小特征值,因此NJW 算法也等同基于Lnor前k个最小特征进行聚类[25]。当采用W进行聚类时,由于公式(1)是基于距离测度的计算方法,而两点间距离最小为0,因此有效区间为[0,+∞]。在公式(1)有效区间内,W的取值均处在0 到1 之间,如图1 红线部分所示。

图1 W 取值示意图
在机器学习特征提取中,最大特征值对应的特征向量方向上通常包含最多信息量[26]。因此,在W特征向量选取过程中选择前k个最大特征值所对应的特征向量。虽然该选择策略可大概率保证选取质量,但仍存在高信息量的特征值不一定有较高的分类贡献信息量问题。
针对特征向量选取问题,王洪森等人[27]与王兴良等人[28]从特征值k值设定阈值入手,扩大选入特征值与特征向量数量。王洪森选取矩阵前3k个特征值并求取平均值记为λ,最终选择λ数值最k近邻的特征值,但对于3k的取值未解释其必然性,且基于均值的选择策略易受样本数量影响,增加时间消耗。王兴良等人提出基于约束分值的特征向量(Bootstrap aggregating,Bagging)选取法。算法选取L前2k个特征向量,并采用成对约束计分方法与Bagging 结合,在特征值选择阶段效果良好。基于Bagging 的选取策略相较均值选择策略而言,向量的选取方式理论依据更强,但也无法避免计算复杂的缺点。
1.3 谱聚类算法存在的不足
由于谱聚类算法应用场景的不断变化,传统谱聚类算无法使小数量标签发挥相应价值、W矩阵构造阶段并未包含数据的多元特征,如部分先验标签信息、空间信息等,W经过谱分解、聚类等操作后,特征缺乏引起的误差将会放大,最终影响最终聚类结果,同时两阶段聚类方式易受二阶段聚类算法缺点影响。在算法时耗方面,传统谱聚类算法因矩阵W与矩阵L计算量大,在处理小样本数据集时聚类性能良好,但处理大规模数据集时,传统谱聚类因数据量过大导致聚类中断。
针对上述谱聚类算法的不足,众多学者不断提出改进算法来解决以上问题,并在现有研究条件下均衡优化算法的时间、空间开销及算法聚类性能。本文基于现有的谱聚类算法优化策略与方向,将谱聚类优化算法划分为以下三类:半监督与距离测度优化、二阶段聚类算法优化及执行效率优化。
2 谱聚类改进算法
随着社会的数字化,谱聚类算法应用范围与场景发生改变,算法及模型需要及时优化与改进才能保持可用性与鲁棒性。
2.1 半监督与距离测度优化方法
机器学习分为无监督学习与监督学习,而现有的数据样本一般仅有少量标签,采用无监督学习数据标签将被舍弃,而少量标签也无法满足监督学习需求。半监督学习结合监督与无监督学习特性,使标签的发挥相应价值,既节省人工成本又避免标签浪费。通过半监督形式发挥标签应有的作用,最终优化算法精确度[29-30],且经过文献[31]实验证明,相比无监督聚类算法,半监督聚类算法的聚类准确率更高,同时半监督谱聚类现今应用于功能磁共振[32]与印刷套准[33]等领域。下面将详细介绍限制与测度两种方法及相关优化策略。
2.1.1 基于先验信息限制方法
基于限制的半监督谱聚类算法采用成对限制先验信息更改W,达到提升聚类性能与准确率目的,这也是限制半监督谱聚类算法的核心思想[34]。而针对谱聚类半监督化思想,Kamvar 等人[35]在2003 年提出并实现基于数据样本自适应的谱聚类算法,该算法同时适应与无监督与有监督聚类并具有较好精度。
半监督谱聚类算法通常采用两类成对限制,即Must-Link(ML)与Cannot-Link(CL)来辅助聚类搜索[36]。当两个样本存在ML 限制时,对应样本划分为同一类,若存在CL限制对应样本划分于不同类中。成对先验信息与相似度矩阵同样具有如下对称性与传递性。
对称性:

对于任意的i、j、q均存在以下传递性:

采用半监督聚类算法时,成对限制先验信息与聚类算法中W对应关系如公式(10)所示:

在理想状况下,xi,xj属于一类Wij=1,否则Wij=0,以上分别对应ML 与CL 情况。通过公式(10),成对约束先验信息直接修改相似矩阵,对聚类进行监督矫正,提高相似矩阵质量,得到更加精准的聚类结果。
通常谱聚类基于现有成对约束,直接聚类的策略对算法提升有限,而成对约束拥有如公式(8)、(9)所示性质,因此成对约束传播可挖掘隐性约束信息。在面向成对约束传播问题,赵晓晓等人[37]提出结合稀疏表示和约束传递的半监督谱聚类算法。该算法在普通约束谱聚类基础上,将约束集合中的数据作为地标点来构造稀疏表示矩阵,获得近似相似度矩阵,同时根据相似度矩阵生成连通区域,在每个连通区域内动态调整近邻点,利用约束传递进一步提高聚类准确率。
对半监督谱聚类算法而言,监督信息的质量、可靠性与数目对准确率影响较大,为避免选取低质量约束,Wang[31]与王娜[24]等人从提升监督信息选取质量入手,提升选取监督信息质量。Wang等人采用主动查询策略替换随机查询策略,并采用主动查询函数来动态选择约束以增强算法鲁棒性;关于谱聚类参数敏感问题,通过采用Hessian矩阵代替拉普拉斯矩阵得到解决。王娜等人提出基于监督信息特性的主动半监督谱聚类算法,采用主动学习策略挖掘数据深层信息如,属于同一类但样本距离较远的样本点信息;或属于不同类但样本距离较近的样本点信息,以上信息均称为高质量信息。低质量约束信息如图2(a)所示,该图中监督信息可通过聚类轻易获得,对聚类监督矫正作用弱,所提供的监督信息对聚类贡献度低。高质量约束信息如图2(b)所示,约束信息e-i=CL、j-g=ML与h-d=CL是通过聚类算法无法轻易获取的高质量信息,因此,通过选取高质量成对约束监督信息,提高监督信息对聚类贡献度,避免因监督信息质量低导致的聚类结果提升不明显等问题。
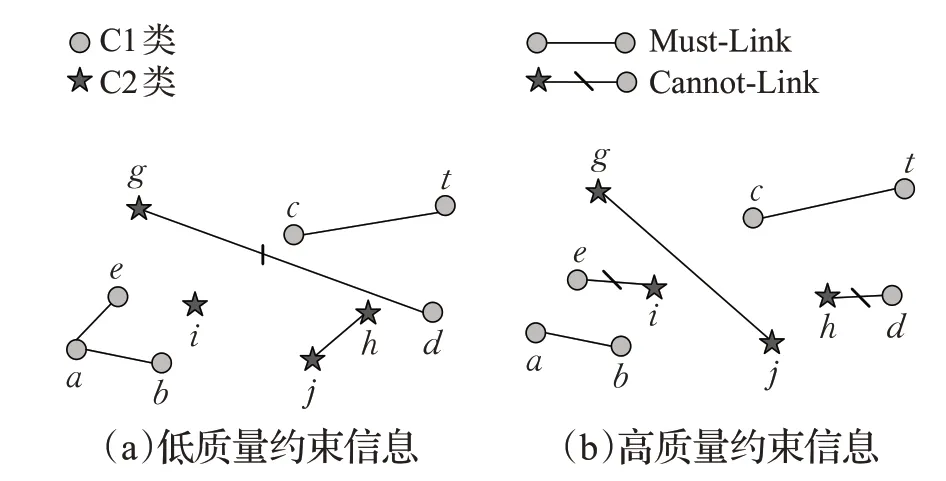
图2 高质量与低质量监督信息示例图
在现实应用中,成对限制信息通常由用户给定、随机选取或主动学习等方式获得。面对真实数据集,算法无法正确聚类样本的对应信息是提高算法精度与性能的关键,同时也是半监督聚类具有约束效力的高质量监督信息。相比于普通约束信息,含有高质量约束信息的半监督谱聚类算法在准确率上有显著提升。
在层次聚类中,Nazari 等人[38]提出的基于交点聚类算法与成对约束信息的传递性类似,该算法通过判断两簇是否存在交点来决定合并操作。如图3所示,基于合并交点簇思想,簇间可通过传递的方式连续合并,这点与半监督聚类中成对约束信息的传递性类似,焦点聚类算不仅简单有效,且在球型的样本表现、性能更优。由此可见,监督信息的传递等特性在聚类中具有普适性。

图3 交点聚类算法示意图
但仅基于成对限制的谱聚类算法在处理流形数据时提升有限,因此肖成龙[39]与杨婷[40]等人受启发于流形正则项,将其与谱聚类结合,以提升谱聚类在处理流行数据的聚类性能。肖成龙等人将约束、正则化与深度谱聚类结合,利用反向传播将约束与正则信息调整权重。杨婷等人利用L2,1范数与成对监督信息构造高质量W,并在此基础上引入流行正则项。
选取质量低或数量少的约束信息易对算法产生误导作用,影响聚类精度,因此选取高质量先验信息形成约束以监督指导聚类。基于已有约束信息通过样本传播,以发现更深层约束信息,最终在约束与相似度矩阵的协同下提升算法准确率。此外仅基于成对约束的谱聚类算法在处理流形分布数据效果欠佳,引入样本密度信息或流行正则项等策略,提升算法在处理流形数据的表现。具体基于先验信息优化策略的对比分析如表1所示。

表1 先验信息策略对比
2.1.2 基于距离测度方法
在基于限制的半监督聚类中,存在限制信息重复导致信息含量小,无法获得进一步提升聚类结果问题。经研究发现,仅基于样本层面的限制先验信息质量较低,无法获得更优解。针对该问题,研究者将基于距离测度的半监督方法引入谱聚类算法,以便构造包含多维特征的W矩阵。基于测度的半监督算法通过对监督信息学习,改变聚类算法中的距离测度函数,得到适合数据聚类的新度量[41-42],最终通过新测度计算W进行聚类。
在面向反应数据全局一致性与空间一致性的测度方面,王玲[17]与陶新民[43]等人均从数据密度特点着手改进算法。陶新民等人基于距离测度,定义含有伸缩因子与密度敏感项的密度敏感距离,通过调节参数到达类内高内聚、类间低耦合的理想状态,且在时间复杂度不变的条件下,提升传统基于欧氏距离的谱聚类对流型样本的聚类性能。该算法同时采用谱熵贡献率[44]、最大熵代替K-means算法等方式来提高算法的准确率。王玲等人则借鉴限制与测度融合方法,采用图最短路径长度生成密度敏感距离测度以计算W,同时成对先验信息对W矩阵进行监督矫正。算法密度敏感距离测度定义与相关步骤如下:
首先用密度可调节线段L代替传统距离:

dist(xi,xj)为数据点的欧氏距离。算法通过密度线段L计算得到密度敏感矩阵,密度敏感距离计算公式如下:

该测度将数据点看作图的顶点V,将数据点间的线段L看作权重E。令p∈Vl表示图上长度为l=:||p的连接点pl和p||p的路径。边(pk,pk+1)∈E,k∈[1,||p]。Pi,j表示连接数据点xi、xj的所有路径集合。
相似矩阵定义如下:

密度敏感距离通过ρ调节线段L的长度,并由L组成矩阵L,通过L计算密度图最短距,形成敏感距离,如公式(11)、(12)所示。利用成对约束信息,直接修改监督点间Dsen矩阵对应数值,含有监督信息的Dsen通过公式(13)得到相似矩阵S。S在含有密度敏感空间信息的同时包含成对先验限制信息,相比于仅采用欧氏距离的传统谱聚类算法,限制与测度融合策略能够保留更多数据特征。由此可见,距离测度的选取在谱聚类算法影响深远,尤其面对高维数据时距离的选择尤为关键。
以上基于密度的优化策略提升效果显著,但存在调节参数较多等问题,针对该问题,刘友超[45]与葛君伟[46]等人通过无参数的密度自适应邻域构建法构建无向图。刘友超等人将相似图与先验信息相结合,在遵循半监督聚类方式下,重新定义既含有成对约束与相似图信息的W。葛君伟等人则以共享最近邻来衡量样本间的相似性度,避免参数带来的误差。基于以上研究基础,赵萌萌等人[47]针对大规模数据应用场景,提出增量式共享紧邻密度的谱聚类算法。该方法将样本随机分为t个子集,在每次增量聚类时采用KNN 确定新增子集数据点的类别。本章举例基于距离测度改进的谱聚类算法,针对不同问题的不同优化策略,算法具体对比分析如表2所示。

表2 测度优化策略对比
2.2 二阶段聚类算法优化方法
谱聚类在低维解空间通常采用K-means 等聚类算法进行二阶段聚类,但K-means算法在选取聚类中心点时具有随机性,存在产生空簇的概率,因此影响谱聚类算法整体准确率与稳定性[48-49]。
为避免引入随机性、提高谱聚类算法的整体稳定性,针对二阶段聚类选取K-means的谱聚类算法,优化初始聚类中心选取策略为常见优化方法。Sapkota[50]、谢娟英[51]及周伟[52]等人通过优化初始聚类中心以提升算法稳定性。Sapkota 等人采用新最远启发式思想(New Farthest Point Heuristic,NFPH)改进的K-means 来代替传统K-means 算法。NFPH 通过哈希表储存样本点对应频率,选取频率最高的样本点代替K-means随机选取的初始聚类中心略,以加强算法稳定性。算法选取流程如图4 所示,当前簇类数目小于设定K值时,通过NFPH 策略选取下一个聚类中心。基于该思想的谱聚类算法与实验对照组相比,错误率低但时间消耗较高。

图4 NFPH中心选取流程图
谢娟英等人选取方差优化初始聚类中心的SD_K-medoids[53]代替传统K-means 算法,提高谱聚类算法整体稳定性,并将相似矩阵参数σ替换为完全自适应的局部尺度参数,使相似矩阵更好表达样本真实分布情况。K-means的优化算法中,赵鑫等人[54]将Canopy算法引入K-means,达到降低算法迭代次数的同时提升算法稳定性的效果。周伟等人将Canopy优化后的K-means算法引入谱聚类以克服初始中心点不稳定的缺点,但基于谱聚类算法的Canopy优化策略使聚类时耗高问题更为突出,处理大规模数据集困难。
针对二阶段谱聚类中K值确定问题,孔万增[16]与胡卓娅[55]等人从特征值本征间隙出发,自适应缺点聚类K值。孔万增等人利用本征间隙特性,自动确定K值,避免手动调参,采用基于矩阵赋零法代替K-means进行二阶段聚类,基于余弦值的矩阵赋零法直接基于矩阵操作,相比于K-means算法时耗更短。该优化策略在实现K值自动确定的同时,避免引入其他聚类算法的不确定性等因素。而胡卓娅等人在利用本征间隙确定K值的同时,在二阶段聚类采用优化蜂群算法代替K-means算法,借助蜂群算法特性增强谱聚类算法全局搜索能力。
上述算法在二阶段聚类分别选取改进的K-means算法或选取其他聚类算法,以提升算法的稳定性。然而每种聚类算法均有相应的优缺点,K-means算法线性时间复杂度是最显著的优点,而基于初始中线点优化策略的K-means算法通常付出更多时间消耗,增加谱聚类算法适应大规模数据负担。因此,选择第二阶段聚类算法时,时间复杂度是值得考虑的因素之一。具体二阶段聚类算法对比分析如表3所示。
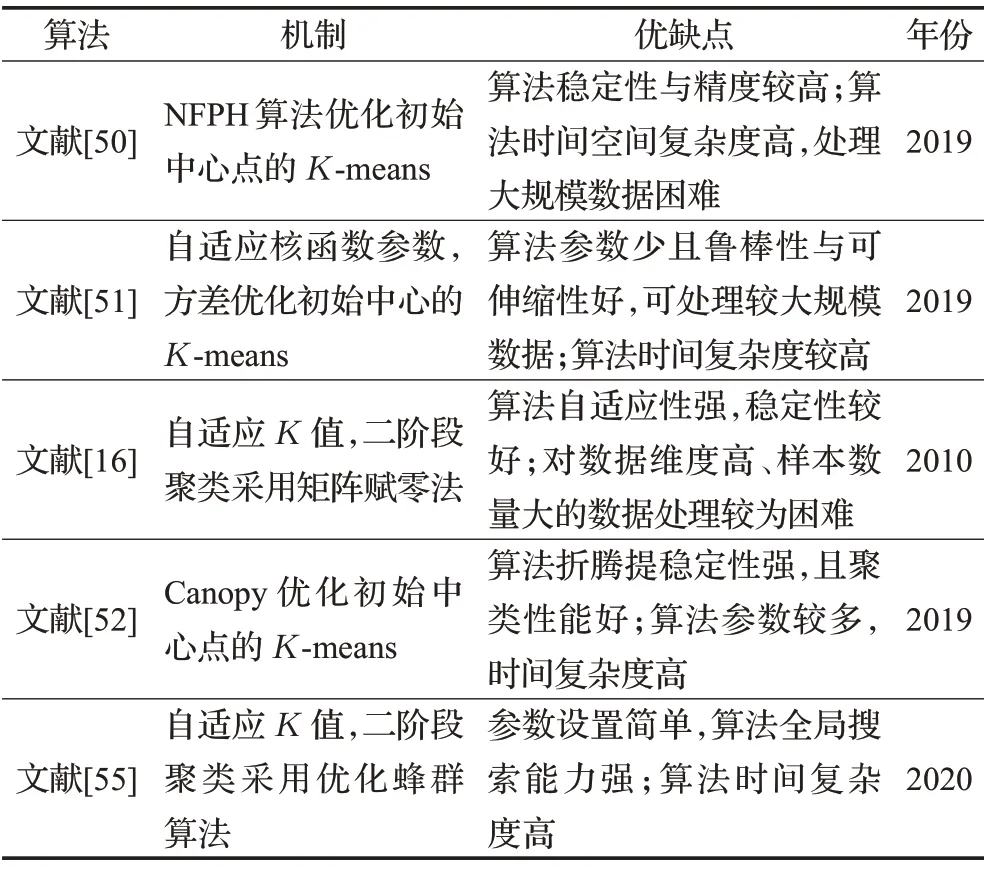
表3 二阶段聚类算法对比
2.3 执行效率优化方法
传统谱聚类算法基于数据样本计算W矩阵并进行规范化,因此算法时间复杂度为O(n3)。面向大规模数据应用场景,谱聚类算法通常因时空复杂度过高,无法完成计算而被迫中断。为提高谱聚类算法在海量数据场景下的可用性,研究者借助Spark 等平台优势对谱聚类算法并行加速,或通过优化W矩阵计算策略减少计算时耗,或针对现有划分模型进行优化,降低算法时间复杂度,减少算法处理海量数据时间开销。
2.3.1 并行与优化改进方法
通信技术的发展使信息生产、传播更加快速,因此,数据体积日渐庞大、种类繁多。面向海量数据的处理诉求,迫使聚类算法提高可伸缩性。Spark 并行框架因内存计算的特性受到广泛关注,且对聚类算法加速效果显著,因此研究者将谱聚类算法与Spark 有机结合。基于Spark 的谱聚类算法通过减少数据计算及数据传输开销,从而降低算法时耗,增强谱聚类算法处理大数据的可用性。
针对基于Spark 的并行策略设计,朱光辉[56]与崔艺馨[57]等人提出算法并行策略。朱光辉等人提出的并行谱聚类算法(Spectral Clustering Algorithm Based on Spark,SCoS)中包含四个主要步骤并行化,分别为:
(1)相似矩阵构建与稀疏化过程并行化;
(2)拉普拉斯矩阵构建与正规化过程并行化;
(3)正规化拉普拉斯矩阵特征向量计算并行化;
(4)K-means聚类并行化。
基于多轮迭代并行方法构建相似矩阵,在减轻主节点压力的同时避免重复计算相似度。t近邻方式对相似矩阵进行稀疏化,达到节省存储空间与减少L矩阵计算量目的。由公式(6)可知,L正规化通过三矩阵链乘实现,时间复杂度高。为降低求解Lnor时间复杂度,通过对角阵D的性质对L进行相应行列变换,即可得到Lnor。针对特征向量的求解,SCoS算法基于Scala PACK实现特征向量并行化求解。崔艺馨等人基于上述研究基础,采用二叉树索引网格划分对并行数据划分,通过边界值划分扩展提升数据分块合理性。
基于Spark的谱聚类算法一般依赖高级语言得以实现,而Julia语言虽然同为高级语言,但性能媲美静态编译语言且专为并行与分布式计算设计。Huo 等人[58]采用Julia 语言实现多处理器并行的谱聚类算法。基于Julia 的谱聚类采用k近邻策略计算W矩阵,并将k个特征值求解看作图分割问题。得益于Julia的易用性与灵活性,算法通过调用ARPACK计算特征向量,且在二阶段聚类采用K-means++提升算法稳定性,最终文章通过实验证明该并行策略的有效性与准确性。
基于分布式平台、语言的并行加速策略虽对谱聚类计算耗时问题有所缓解,但存在为减少时间消耗导致数据信息丢失影响算法准确率问题。因此,Wu 等人[59]提出如图5所示的随机装箱(Random Bining Features,RB)算法,采用RB算法得到矩阵Z代替相似矩阵W,并对后续特征分解加速。该方法应用BR特征矩阵内积近似表示W,避免相似矩阵计算。采用预处理迭代多方法特征求解器,降低L矩阵特征分解时耗,最终得到线性时间复杂度的谱聚类算法,且优化后的谱聚类算法时间开销更少,对大规模数据适应良好。

图5 RB算法流程图
上述算法因优化出发角度不同而略有差异,在矩阵计算阶段,Spark 环境下的谱聚类算法通过多轮迭代的方式避免重复计算数据间相似度,而基于RB 优化的谱聚类算法通过计算落在同一网格内数据点的相似度来减少计算开销;在拉普拉斯矩阵求解阶段,前者利用稀疏相似矩阵的特性,进行相应行的操作得到Lnor,后者采用近似相似矩阵Z与度矩阵公式转换得到L矩阵。以上优化策略算法加速工作较为完善,但未像基于Julia的谱聚类算法一样,考虑第二阶段聚类算法对算法整体聚类性能、准确率等方面影响。
2.3.2 谱图划分改进方法
谱聚类算法受谱图划分思想启发,通过构造数据有权无向图并逼近最优图划分,进而求解聚类问题,而图划分结果与切割准则密切相关。随着样本类别、数目、维度及数量等特性的改变,对划分准则进行相应改进以提升谱聚类算法聚类精度及可伸缩性。
Chen等人[60]直接优化规范切割准则,得到直接规范切割模型(Direct Normalized Cut,DNC)。通过DNC来对规范切割模型进行直接运算,将算法时间复杂度降至O(n2c)。针对大规模数据处理,以DNC 为基础提出快速规范切割法(Fast Normalized Cut,FNC),FNC 使用均衡K平均值算法,将数据分为均衡子集并采用子集中心为Anchor(锚点),计算锚点与整个数据的相似矩阵,最终通过DNC得到聚类结果矩阵Y。
相较于其他改进策略,DNC 对目标函数进行改进使目标函数收敛,并对问题进行求解,将谱聚类算法时间复杂度降为二次。FNC算法通过均衡K-means算法通过锚点采样以减少相矩阵计算,并达到线性时间复杂度,且在人造数据集与真实数据集上均表现出色。
2.3.3 其他快速优化方法
基于锚点图的模型被提出以应对规模快速增长的数据,当谱聚类算法采用锚点模型聚类时,使用过于稀疏的锚点会降低算法性能,而锚点密度足够大时,算法时间成本显著增加且处理困难。针对该问题,YANG等人[61]通过构建金字塔多层锚点,如图6所示,并利用原始数据层H0 与最后锚点层Hm构造层次二分图,旨在减少相似矩阵计算量与时耗。图6(a)为金字塔模型示意图,其中H0 为原始数据层,H2、H3 为锚点层。图6(b)展示了H0 层与锚点层的分布与选取情况。
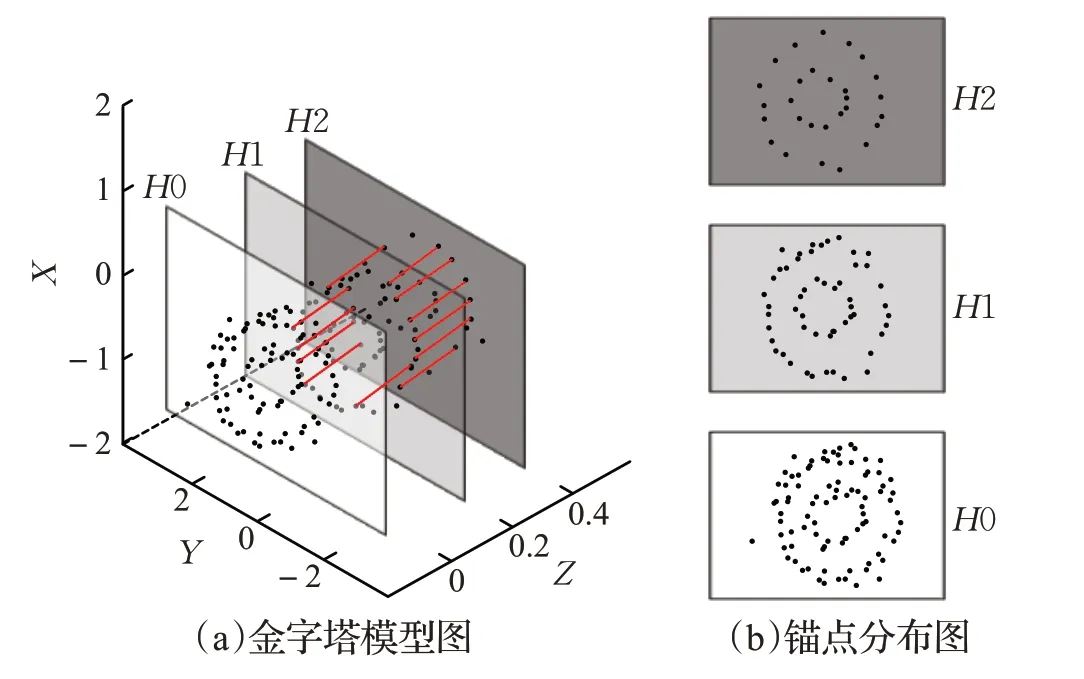
图6 三层金字塔Anchor示意图
在锚点图模型当中,选取锚点的质量影响聚类效果。因此,采用如下混合数据代表点选取方法[62]。
(1)随机选取P个候选点(其中p (2)在P上运用K-means 算法选择p个簇类中心作为最终代表点,并记作R={r1,r2,…,rp}。 混合数据代表点选取方法在更好捕捉数据结构特征的同时降低算法计算量与时耗。 Nyström通过对数据近似计算来逼近真实的特征空间,从而降低计算复杂度,因此谱聚类算法可以通过Nyström 采样法提升算法可用性。丁世飞[63]、刘静姝[64]及邱云飞[65]等人从采样角度出发,寻求谱聚类与海量数据采样契合点。丁世飞等人采用自适应采样方法多次遍历采样,每次采样后更新剩余点采样概率以提升采样质量。最终在牺牲较少精度条件下,达到大幅降低计算复杂度、提升算法稳定性的目的。刘静姝等人在Nyström基础上运用乘法更新原理,实现分类指示矩阵更新,避免高时耗谱分解步骤。相比于传统谱聚类算法,该策略在处理高维数据时更快速。邱云飞等人则针对Nyström方法选取样本代表性弱问题,将加权思想引入,基于加权数据K-means聚类中心点采样,且在Nyström阶段采取并行处理方式提升集成多样性与高效性,最终大幅降低算法复杂度。 在提升算法运行效率方面,基于分布平台并行加速策略通常对平台依赖性较高,且并行聚类结果合并方式直接对算法结果精度产生影响。而为降低算法计算复杂度与时耗,采样方式难免引入随机性的干扰,导致算法聚类精度有所下降。算法执行效率优化策略具体对比分析如表4所示。 表4 执行效率策略对比 谱聚类的三类优化策略各有侧重点,优化策略彼此互相借鉴成为近年谱聚类算法优化的热点。每类优化策略特点不同,如限制策略注重样本局部信息,距离测度策略侧重样本整体分布,两策略相辅相成。谱聚类的具体优化方法、策略对比分析如表5所示。 表5 优化谱聚类算法对比 本章首先对谱聚类常用的相关数据集与评价指标进行简要介绍,基于部分数据集与评价指标,选取谱聚类及代表性谱聚类优化算法对比实验,最终通过实验进行对比分析。 谱聚类算法所采用数据集一般分为两类,一类是以UCI 数据集为代表的小样本数据集(https://archive.ics.uci.edu/ml/index.php);另一类是以图像数据集为代表的大样本数据集。表6、表7 对常用的两类数据集的特点与特征进行相关总结。 表7 常见谱聚类算法图片数据集 采用准确率Acc(Accuracy)、兰德指数RI(RandIndex)、调整兰德指数ARI(Adjusted Rand Index)、标准互信息NMI(Normalized Mutual Information)、调整互信息AMI(Adjusted Mutual Information)等不同的关键性能指标,对谱聚类算法进行评价,相关公式如下: 公式(14)中,N为样本数量,分别为聚类结果与数据标签,K为簇类个数,δ(x,y)函数当且仅当x=y时值为1,否则为0[57]。 公式(17)中,MI(X,Y)为变量X、Y之间的互信息,H(X)为变量X的熵。 本节在Iris、Wine、Ionosphere、Glass 以及手写体数据集上,采用不同谱聚类算法进行实验对比,并进行分析总结。列举近几年代表性的谱聚类优化算法的实验结果,并在数据集上进行实验对比与数据分析。实验采用CPU 3.6 GHz、32 GB 内存、Windows10 操作系统,编程环境PyCharm2020.2.2、python3.8。为客观性地对比算法的聚类指标,实验将谱聚类(SC)算法与随机约束谱聚类(RCSC)算法分别在各个数据集上执行10次,并计算其聚类的平均指标。 该实验分为两个部分:实验一为基于UCI小样本数据集的SC算法、RCSC算法以及基于低密度分割密度敏感距离的谱聚类算法(Low Density Separation Density Sensitive Distance-based Spectral Clustering algorithm,LDSDSD-SC)算法对比分析实验,以上三种算法在UCI数据集上的关参数及兰德指数如表8所示;实验二为基于手写体数据集的大样本分析对比实验,其中SC算法、CSoC 算法、FNC 算法以及基于层次二分图谱聚类算法(Spectral Clustering Based on Hierarchical Bipartite Graph,SCHBG)算法在手写体数据集上的准确率与标准互信息如表9所示。 表8 基于UCI谱聚类算法对比 表9 基于手写数据集上谱聚类算法对比 实验一中,由表8中兰德指数在不同数据集上整体对比可知,谱聚类算法在样本数量小且数据较为平衡的数据集上,如Iris、Wine聚类性能良好,而在样本数据不平衡数据集上,如Ionosphere、Glass 聚类性能稍逊。在Iris与Glass数据集上,基于密度距离改进的LDSDSD-SC[43]算法聚类性能最优,证明基于密度距离改进策略的优越性。而Wine 因数据特征间数值差过大,导致直接聚类效果差,因此,在CS与RCSC算法中对数据集进行归一化处理,故SC与RCSC算法聚类性能明显优于LDSDSDSC[43]算法,这也体现了数据预处理步骤的重要性。观察Ionosphere数据,相比于SC算法基于半监督优化的RCSC算法聚类性能会更优,但RCSC优化策略具有随机性聚类结果不稳定。 实验二中可由Acc与NMI数值观察得知,在MNIST数据集及USPS 数据集上,基于锚点的层次二分图改进策略聚类性能显然更优,而SC算法聚类MNIST这样大规模数据集存储需求大,在实验过程中内存溢出导致聚类中断,因此从对大数据处理方面证明SCHBG 算法优化策略的优异性。观察CSoS算法NMI值可知,仅采用Spark 平台加速对谱聚类算法的提升有限,与其他优化策略如稀疏化等,可对谱聚类算法性能明显提升。 近年来,谱聚类因其独特的优点与特性引起学术界大量关注,经过研究者们不断改进谱聚类算法性能逐级提高,但以下方向需要进一步研究。 (1)利用数据局部与全局先验信息构建相似矩阵 W矩阵是谱聚类算法误差来源的第一环,现有构建W矩阵的方法众多,如本文所介绍的基于限制的谱聚类算法,该种方法虽然利用少量标签实现对W的优化,但并未使用其他方面的先验信息,例如,密度先验信息,且该方法时间复杂度较高。因此,在现有算法改进基础上深入研究,结合多方面特征来构造相似矩阵W,进一步提高谱聚类算法的精确性并降低时耗,也是未来提高聚类算法的一个重要的研究方向。 (2)利用矩阵理论与数据特征自动确定参数 对于聚类算法而言,算法结果对参数的选择十分敏感。谱聚类算法参数一般为核函数参数与类数K,不同的参数生成不同的W,因此参数选取对聚类结果影响明显。针对类数K的确定,本文所介绍自动确定K值的谱聚类算法,通过利用本征间隙特征来确定K。该方法实现K值自动确定,但涉及较多计算与排序。可借鉴目前其他聚类算法自动确定参数策略,并进行相应改进后应用在谱聚类算法上,达到自动确定参数目的。针对大样本数据,高效快速自动确定K值也是谱聚类算法一个值得研究的方向。 (3)海量数据抽样预处理提升算法性能 针对基于大量数据的样本数据不均匀问题、传统谱聚类算法时空复杂度高,无法适用于较大数据样本等问题。聚类算法需要进一步解决,虽然基于Spark 平台及二分图等方式可对算法进行加速,降低算法时耗,但针对算法自身优化来降低时间复杂度仍旧是该领域的未来研究热点之一。 (4)启发式算法向谱聚类算法迁移应用 现阶段,以蜂群算法等为代表的启发式算法与谱聚类算法结合已有研究,且已通过相关实验证明其有效性。因此,将谱聚类算法与启发式算法进行有机结合,借鉴其优化算法思想,并根据谱聚类算法的特性进行调整,形成吸纳新型算法的优点的优化谱聚类算法,不但提升谱聚类算法聚类效果,而且形成新优化方法,这也将成为未来谱聚类算法研究方向之一。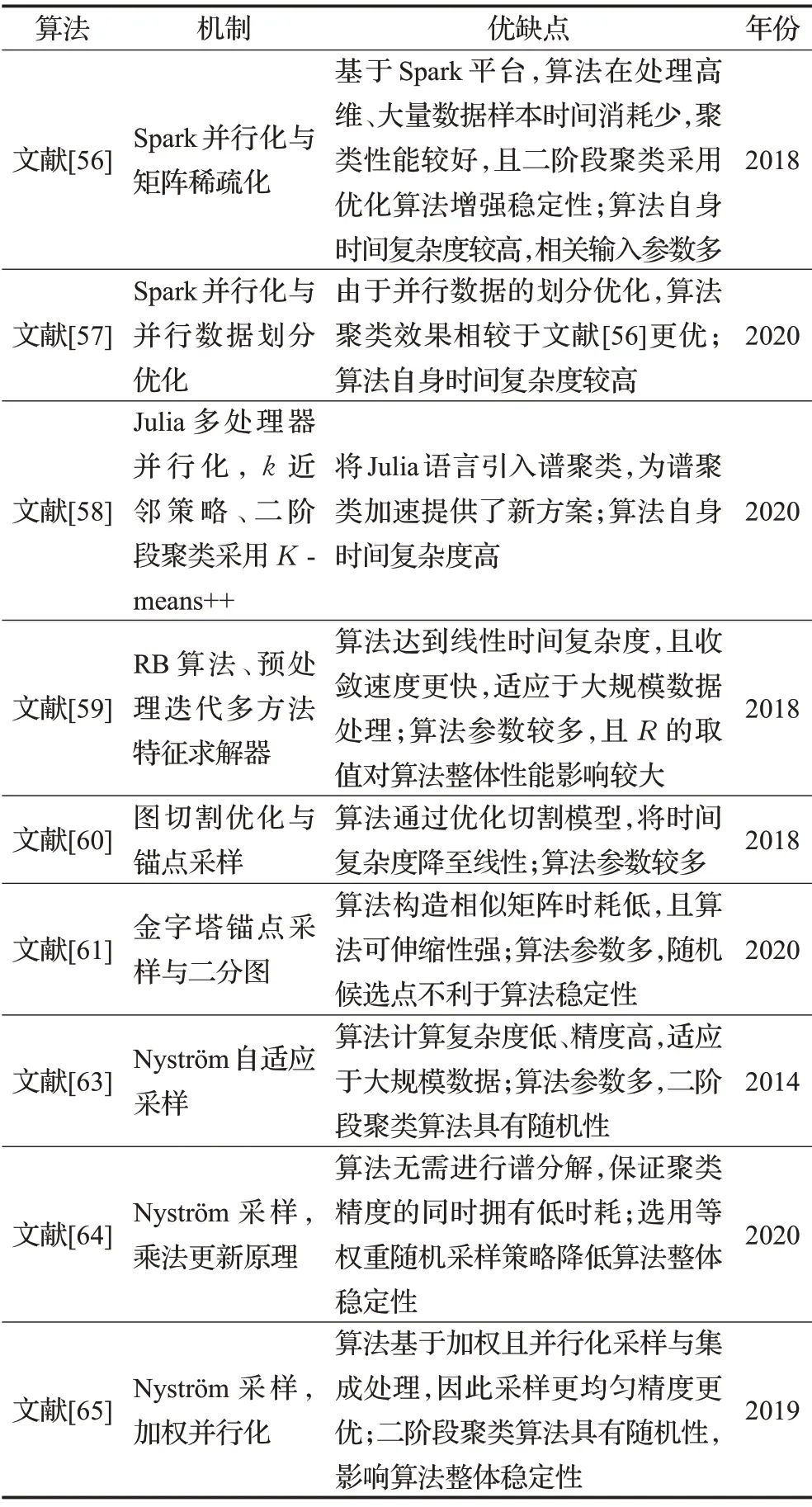
2.4 谱聚类优化方法小结

3 数据集与算法性能比较
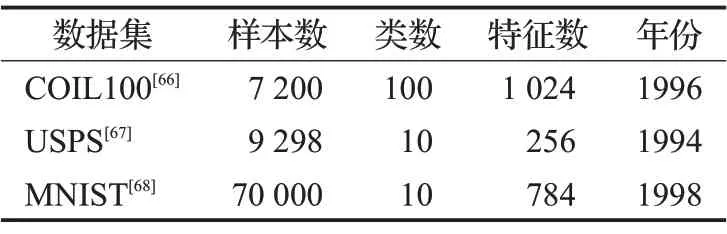
3.1 数据集
3.2 评价标准

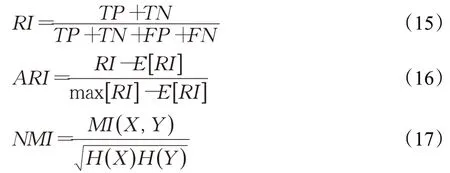
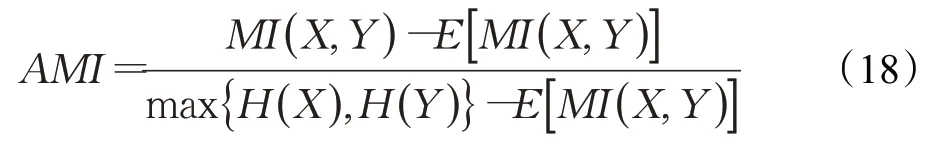
3.3 实验结果与分析


4 结束语
