基于节点配置策略的有分流换热网络优化性能探析

2021-07-28徐玥崔国民

化工进展 2021年7期

徐玥，崔国民

（上海理工大学新能源科学与工程研究所，上海市动力工程多相流动与传热重点实验室，上海 200093）

换热网络优化问题是化工领域研究最广泛的问题之一，其通过热、冷流股之间的合理匹配，可实现系统能耗的减少和经济效益的提升。为此，在设计阶段构造高效、灵活、编译简单的优化模型可成为辅助换热网络问题发展的重要突破。

Yee 和Grossmann[1]提出的分级超结构模型（stage-wise superstructure model，SWS）是典型的结构化模型，在模型的每一级内可完成冷、热流股的全匹配，并通过多级设置扩增其求解域。但其对于SWS 模型有诸多限制，如将公用工程置于流股末端；热、冷流股上分支数目需等于冷、热流股的流股数目；为简化模型计算，采用等温混合的方式；禁止分支上连接多个换热器以及旁流结构等，使得SWS 模型的能力受到一定的限制。为提高求解质量，针对SWS 模型的改进方法可分为以下几类：将公用工程作为流体参与换热[2]以增加匹配的多样性；在分流结构中添加公用工程，提升结构变异的能力[3-5]；引入多种公用工程[6-7]，在实现网络能量平衡的基础上，减少年综合费用。此外，Liao等[8-10]在原转运模型的基础上，增加了分流、旁流、环流等结构，并引入了传质过程，该模型有效提升了优化质量。虽然以上针对结构化模型的方法均促进了优化结果的提升，但同时增加了网络中的优化变量，其固定的匹配模式在优化中引入大量无效分流结构，对寻求优质结果形成阻碍，尽管一些改进策略可提升算法搜索能力，但也相应增加了算法的复杂度，降低了优化效率[11-13]。

为打破模型的模式化匹配对优化进程造成的影响，肖媛[14]、Xu 等[15]提出了节点非结构模型（nodes-based non-structural model，NNM）。NNM模型的设定相对自由、灵活，换热器的生成可表示为任意两个空置节点的连接，与结构化模型相比，NNM 模型可在有限节点的设定下为算法提供更多的潜在结构。此外，在有分流NNM 模型中，换热器串联数目、分流数不受算例流股数目的限制，可根据经验自行设定，减少了无效变量的引入，提高了求解效率[15]。

在分析NNM 模型优化过程及结果时可发现：NNM 的模型参数设定依然采取统一的方式，即NNM 模型中所有热流股共用一组模型参数，冷流股共用一组模型参数。因此，为使模型得到更优的结果，在设定流股的分流数时，需分别满足热、冷流股中分流最多的需求。从算例的流股参数及大量优化结构配置的分析中可知，不同流股对于分流的需求不同，同一类型的流股共用一组节点参数会造成部分分流的浪费，影响优化效率。为实现各流股的个性化匹配需求，提高网络中分流结构的利用率，本文提出了节点配置策略。该策略可根据各流股性质调节分支数和分流组数，在网络节点数一定的前提下，通过对节点的合理化配置，促使有效结构的生成，引导算法寻得更优结果。

1 数学模型及优化算法

1.1 节点非结构模型

节点非结构模型（NNM）是新型的换热网络优化非结构模型。在NNM 模型中，换热器的位置通过网络中设置的节点位置量化标定，流股上的分支数、分流组数以及串联结构中的节点数均可根据算例的规模及其优化难度自行设置。

NNM 模型中节点配置设定如下：NfH，nfH=1,2,…, NfH表示热流股上的分流数；NfC，nfC=1,2,…,NfC表示冷流股上的分流数；MbH，mbH=1,2,…,MbH表示热流股分支上串联的节点数目；同理，MbC，mbC=1,2,…,MbC表示冷流股分支上的串联节点数目；热、冷流股上分流组数分别用NdH，ndH=1,2,…,NdH和NdC，ndC=1,2,…,NdC表示。基于以上设定，单股热流股上的节点数目NeNH和单股冷流股上的节点数目NeNC计算如式(1)、式(2)所示，热、冷流股上总节点数NtH和NtC计算如式(3)、式(4)所示，热、冷流股上总分流数NSPH和NSPC计算如(5)、式(6)所示。

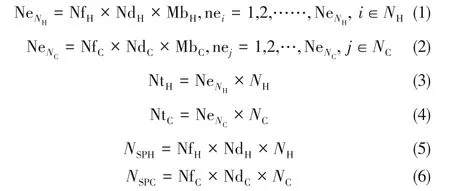
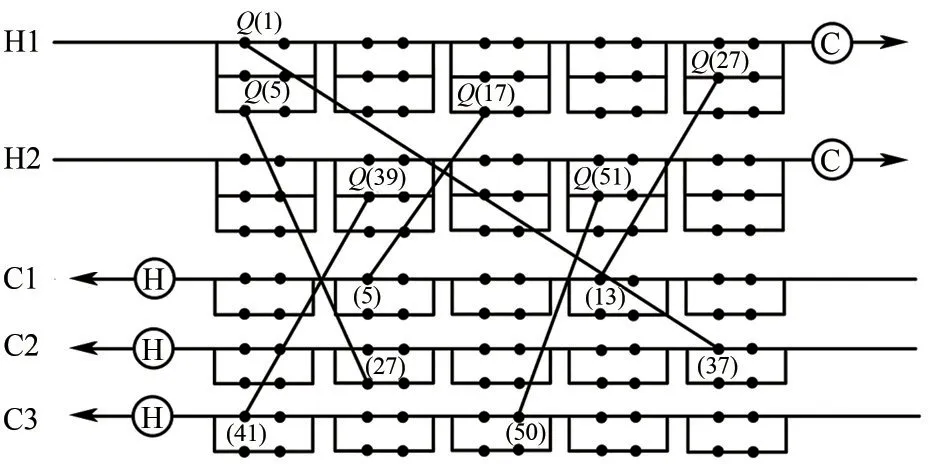
图1 NNM模型结构

以小规模算例H2C3为例，将NNM模型结构图绘制如图1所示。其中节点参数的设置如下NfH=3，NfC=2，MbH=MbC=2，NdH=NdC=5。图中给出了6 个换热器的匹配方式，换热器的位置可用节点的序号进行标定，图1中以括号内数字表示。

1.2 目标函数

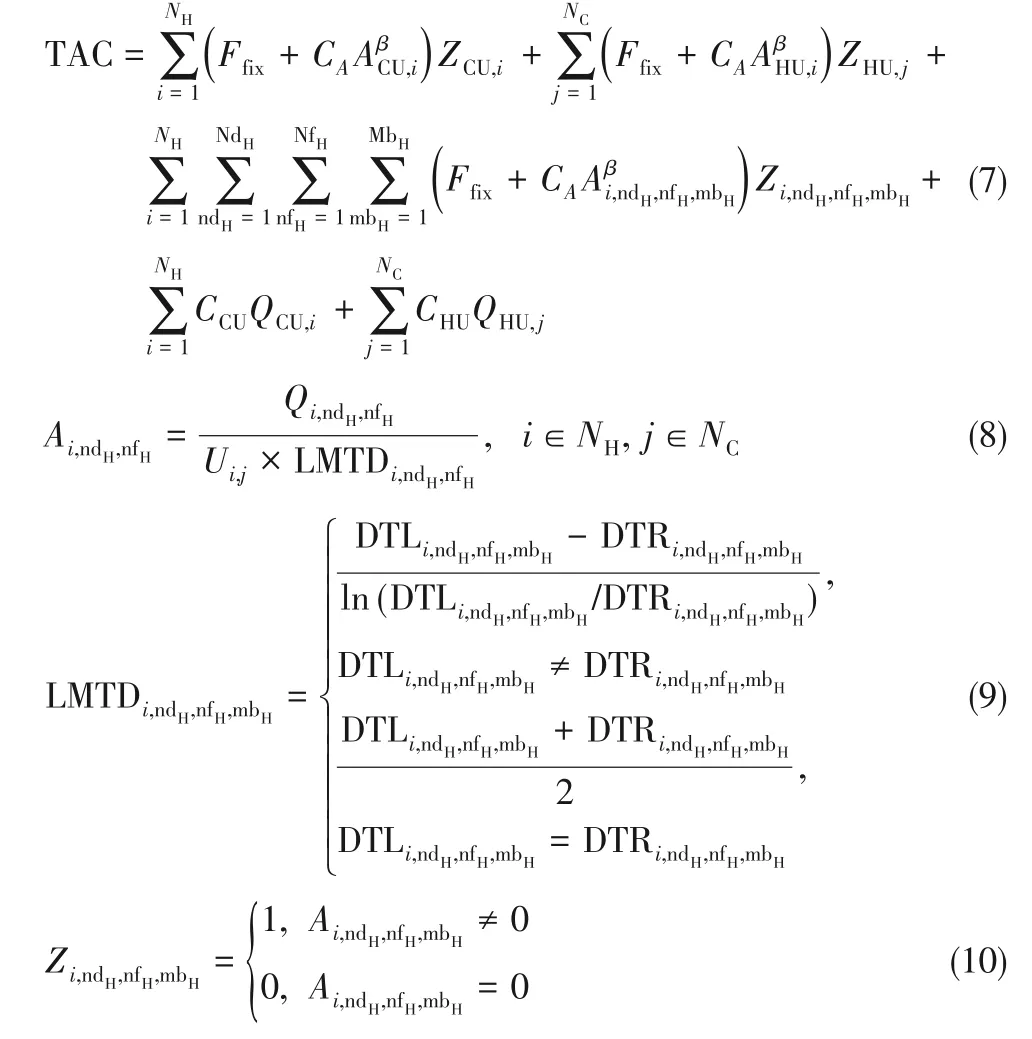
换热网络优化问题的目标函数为年综合费用（total annual cost，TAC），根据模型设定，TAC 的计算式如式(7)所示。年综合费用由投资费用和运行费用组成，式(7)前3项分别为冷公用工程、热公用工程及换热器的投资费用，其中A为面积，Q为换热量，Ffix、CA、β分别表示投资费用中的固定投资费用、面积费用系数以及面积费用指数；后两项为冷公用工程和热公用工程的运行费用，CCU、CHU为冷、热公用工程的单位费用系数；Z为二元变量，表示所处位置是否有换热器，当换热器存在时Z=1，否则为0，其中换热器的面积以式(8)、式(9)计算，其中LMTD 为对数平均温差，DTL、DTR 表示节点左、右两端的温差，Z的取值规则如式(10)所示。

1.3 约束条件

（1）流股上的热平衡［式(11)、式(12)］

（3）冷、热公用工程热平衡［式(15)、式(16)］

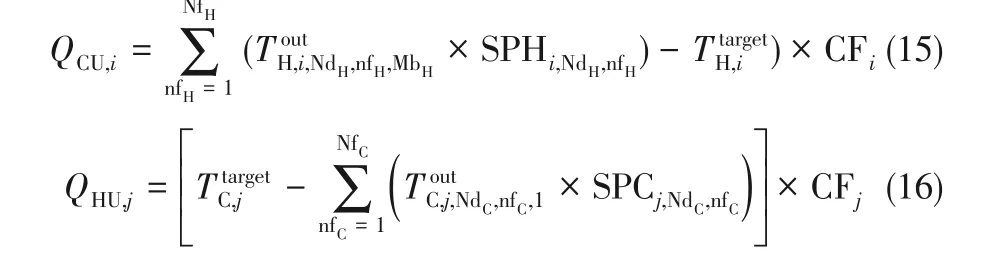
（4）冷、热分流比相关约束［式(17)、式(18)］

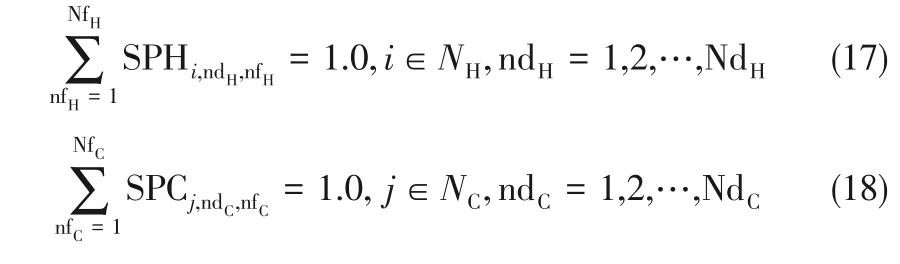
（5）温度可行性约束及温差约束网络中的温度约束可保障热流股的温度从入口温度到目标温度递减，冷流股的温度从入口温度到目标温度递增，具体如式(19)～式(23)所示，其中涵盖了换热单元面积及换热量的非负约束。

1.4 强制进化随机游走算法

文中采用的算法为强制进化随机游走算法[16]（random walk algorithm with compulsive evolution，RWCE）。该算法通过调节换热器的换热量实现网络中整型变量和连续型变量的同步优化。同时，以一定的概率（δ）接受差解，提高了算法全局寻优的能力。RWCE算法是目前相对高效的启发式算法之一，算法具体流程如图2所示。

2 NNM 模型中节点参数对优化结果的影响分析

采用NNM 模型优化换热网络时，有效的分流可促进优质结构的产生，而无效的分流则会制约结构变异，对搜索全局最优值造成障碍，因此分流的设置直接影响结果的优劣。在分析大量算例的网络结构中分流所在流股及数目时发现：①分流结构在热容流率较大的流股上出现的频率较高，可多次利用其温度对不同流股进行换热；此外，热容流率相近的流股易于匹配，利用分流对热容流率较大的流股进行处理后，可增加该流股与其他流股匹配的概率，促进结构中整型变量的变异，提升算例优化质量的提升。②不同流股对于分流的需求不同。网络中存在一部分流股，无论初始分流如何设置，流股上始终无法生成分流或其分流常使算法停滞于局部极值。

在NNM 模型的设定中，热、冷流股各采用一组节点参数，这导致节点参数的设置既要满足所有流股对分流的生成需求，又要保障算法不会因网络中节点数目过多难以跳出局部极值。因此，节点参数的配置问题仍需进一步讨论。以10SP算例为例，其来源于Ahmad[17]，参数见表1。

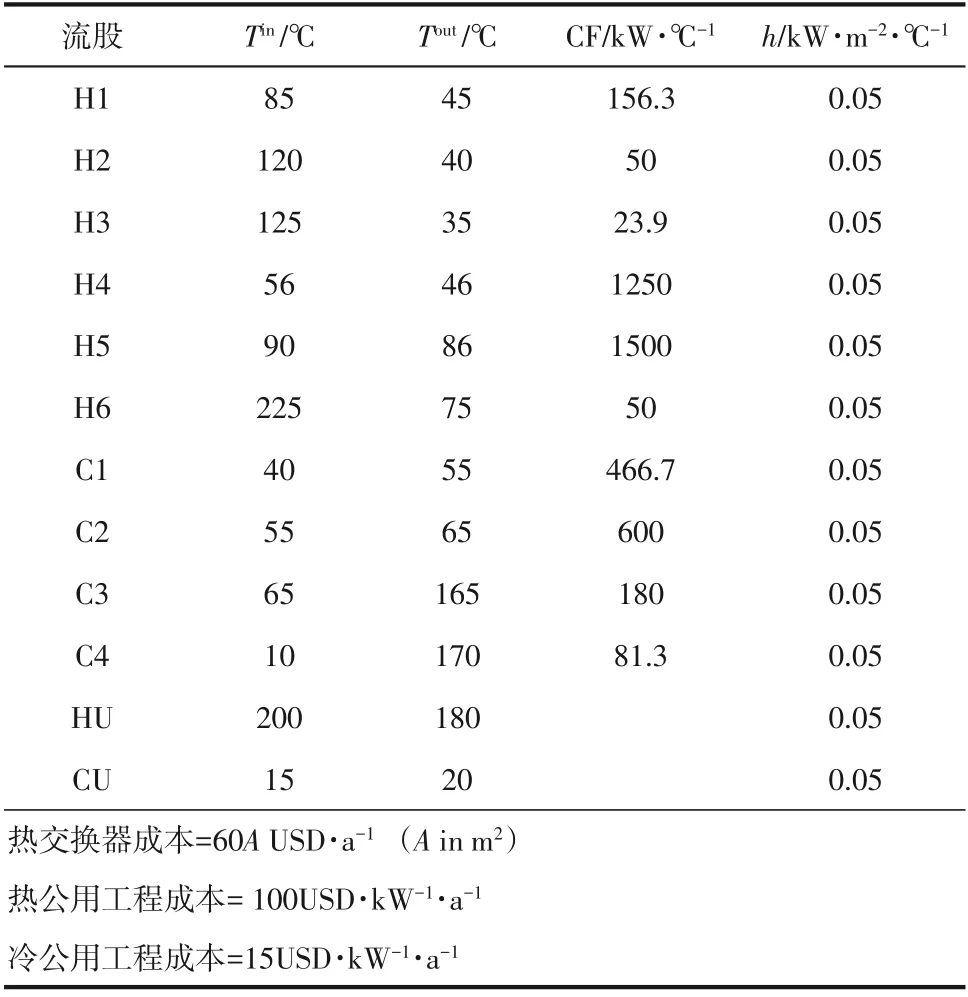
表1 10SP 算例参数

表1给出了各流股热容流率，从数据的对比可知，热流股中热容流率最大值和最小值相差62.8倍；冷流股中热容流率相差5.74倍。为证实节点参数对算例结果的影响，表2给出了5组不同初始节点参数设定下8000 万次迭代后的结果对比。其中测试组A 中NeNH=NeNC=30，测试组B 中NeNH=NeNC=24，R-NfH和R-NfC分别表示优化结果中热、冷流股上出现分流的次数。

从表2中数据可知如下结果。

（1）在网络节点总数相同时，不同的节点参数对结果影响较大，其中A组中最好和最差的结果相差1957USD/a，B组中结果相差1219USD/a。

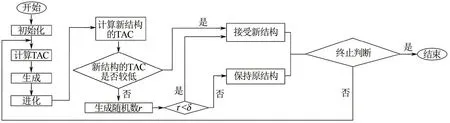
图2 RWCE算法流程

表2 不同节点参数下10SP算例的结果

（2）所有测试结果中的分流均在冷流股上生成，且分流数及所在流股随节点参数的不同有所变化，这表明网络中节点的配置关系影响结果中分流的次数。从A组数据可知，在总节点一定时，增加冷、热流股的分流支数时，网络中易生成分流，但不合理的分流会造成结果陷入局部极值无法脱离。

（3）10SP算例在测试中主要在C1、C2、C4上生成分流，且所有结果在C1流股上均生成了分流，这表明在C1 流股上保留较多的分流结构有利于获取更优的结果；对比B2 和B3 可发现，减少C4 流股上的分流可使得结果降低586USD/a，表明限制C4 流股上分流结构的生成，可减少局部极值结构的生成阻碍算法获取更优结果。

（4）测试组中C2 流股上生成分流导致优化停滞于局部极值中，但文献较优结果[18-19]的结构均在C2 上生成分流，其原因为RWCE 中参数的设置影响到对潜在结构的取舍[20]。综合较优文献中10SP结果，在参数合理的前提下，C2 上保留其分流能力可促进算法获取更优的结构。

根据以上几点分析，NNM 模型中节点数一定时，合理调控流股上分支数和分流组数，可推动优化结果的提升，但同属性流股上采用一组节点参数时，却很难协调不同流股对分流的需求。由于采用RWCE算法优化时，优化结果是多参数组合后的共同作用，因此适用于该算例的节点配置不一定适用于其他算例。基于以上原因，虽然本文无法给出具体的影响规律，但以上分析为后续节点配置策略的提出提供了思路和依据：①应根据算例特点合理地配置流股的分支数，过多的分支设定会使得算法陷入局部极值；②原NNM 模型的节点参数配置为定式配置，而在网络的总节点相同时，不同的节点配置方式对结果有一定的影响，但原模型的参数设定很难同时满足有所流股的分流需求，因此优化质量较差或优化效率较慢。基于此，应根据流股参数对其进行导向性的配置，提高网络中节点的利用率，辅助算法避开无效结构对优化造成的阻碍，快速得到潜在的优势结构，提升算法的优化质量和优化效率。

3 节点配置策略

基于NNM 模型的特点，提出了节点配置策略（nodes' adjustment strategy）。该策略可根据算例中各流股的热容流率，调控其在模型结构中的分支数和分流组数，使得热容流率较大的流股保留较多的分支数，而热容流率较小的流股上产生较多的分组数。选择的函数应该满足以下几点：①流股的分支数应随着热容流率的增加保持单调递增的关系；②在两股流股的热容流率较大时，热容流率较小的流股上应尽量保留一定的分流，热容流率相近的流股，其分流数也应相近。根据上述要求，本文采用三角函数调控容流率和分支数之间的关系，具体表达如式(24)～式(27)所示，式中CFH,MAX、CFC,MAX为热、冷流股上热容流率的最大值，CFH(i)和CFC(j)为第i股热流股和第j股冷流股的热容流率；α为随机数，用于调控各流股的分支数，NFH及NFC分别为热、冷流股的初始设定值。式(24)和式(26)为热、冷流股分支数的调节方式，式(25)和式(27)为对应流股分流组数的调节方式。经该策略的调整，该策略依据流股的热容流率进行个性化的节点布置，为算法获取更优质的结构提供了导向性辅助。

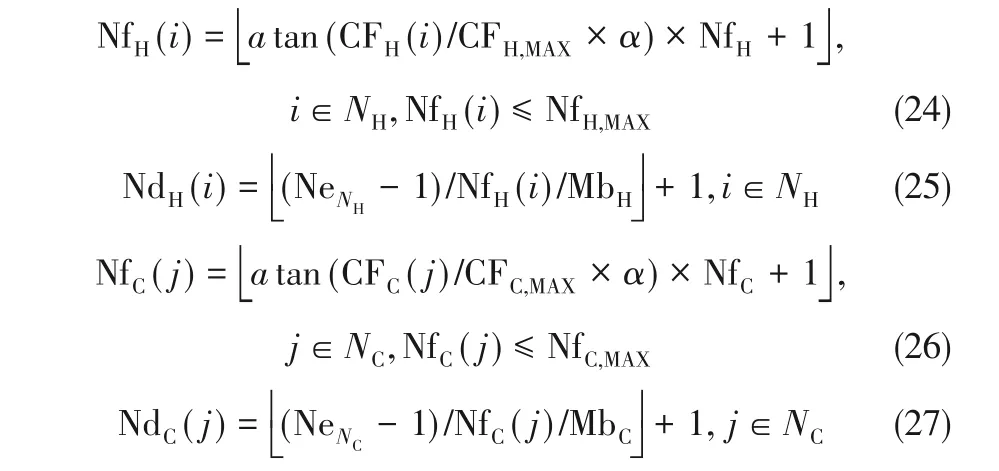
图3 给出了加入节点配置策略的NNM 模型（nodes-based non-structural model with adjustment strategy，NNM-AS）调节流股节点配置的示意图。以分支单节点的NNM 模型为例，由图中可知，经节点配置策略调整后节点可依据流股属性调控，且调整后的流股上可兼备有分流和无分流两种节点配置，保障流股分流能力的同时调整了求解域。

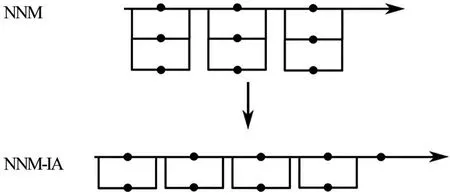
图3 应用NNM-AS调节流股节点过程

4 算例分析

4.1 10SP算例

采用NNM-AS 模型处理后，10SP 各流股节点配置见表3，初始节点参数为NdH=NdC=10，NfH=NfC=3，MbH=MbC=1。根据流股热容流率，热流股中H4、H5 上分流支数为3，其余流股均为无分流流股；冷流股中C1、C2 上分流支数为3，其余流股上分流支数也受到一定的限制。

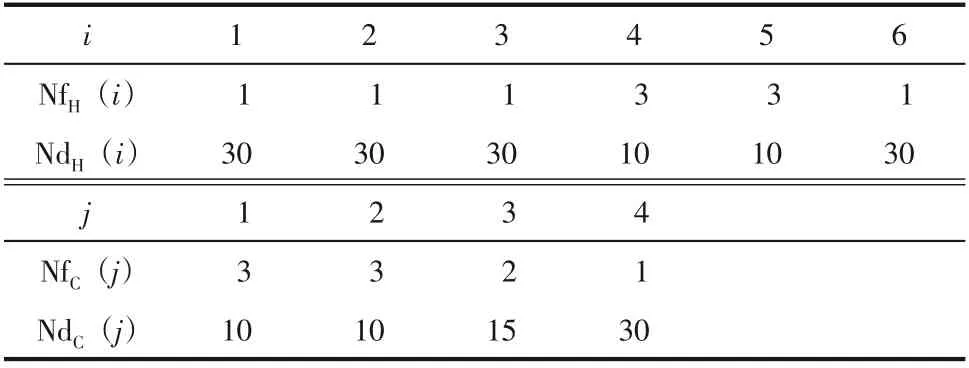
表3 NNM-AS模型中10SP算例各流股节点配置

在此节点配置下，优化可得10SP 结果如图4所示，节点处括号内数字为该节点的出口温度，TAC=5585292USD/a，较目前文献中最优费用低340USD/a，结果对比见表4。从结构对比看，图4中结构相较其他文献中结构已产生较大的改变，换热单元数目也大幅度提升。因10SP 中不含固定投资费用，网络中换热量之间的制约限制结构变异，通过改进后的策略进行优化，可打破原有设置的限制突破局部极值。由表3可知，H4、H5、C1、C2、C3以有分流模式参与优化，而H1、H2、H3、H4、C4 以无分流模式参与优化。NNM-AS 模型兼顾了分流和无分流两种模型，由此可获得更多的潜在优势结构。

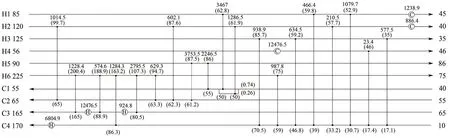
图4 采用NNM-AS优化10SP算例结果（TAC=5585292USD·a-1）

在相同参数设置下，分别采用NNM-AS 模型与NNM 模型用于RWCE 算法优化10SP，探究改进后模型对优化效率的提升效果，其TAC 随迭代次数变化如图5所示。

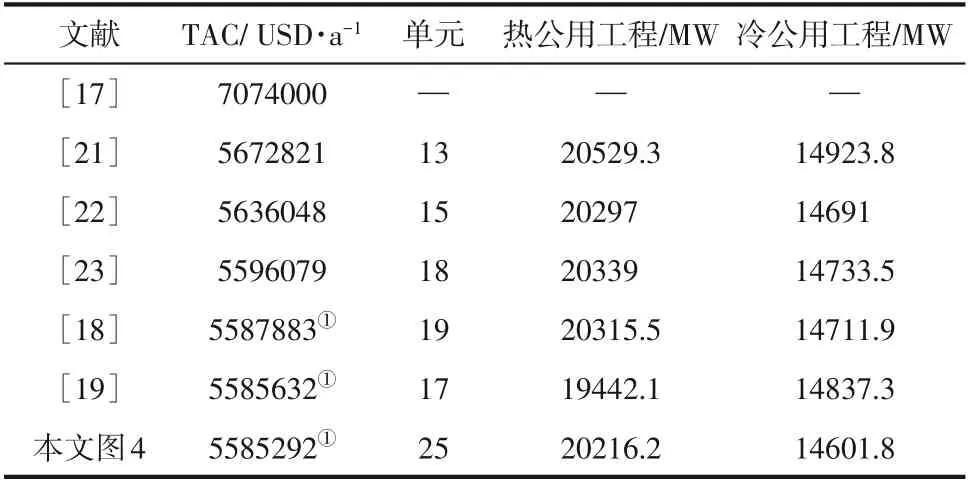
表4 10SP算例结果对比

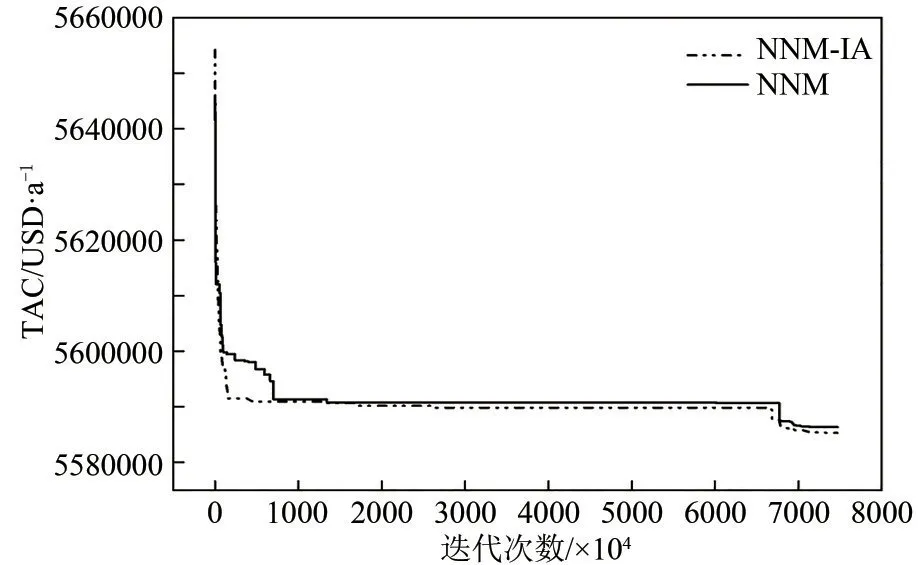
图5 NNM-AS和NNM模型优化10SP算例结果对比

从TAC 曲线变化可知，在对网络中节点进行导向性配置后，抑制了网络中无效的分流结构，使得算法在优化初期便可找到较优的结构，并在整个优化过程中始终处于优势地位，在7500 万次迭代中获得TAC=5585292USD/a，而此时以NNM作为优化模型获得的TAC=5586224USD/a。由此可知，NNM-AS模型可有效辅助算法提升效率。

4.2 15SP算例

算例来源于Björk等[24]，流股参数见表5。由于优化算法的贪婪性，8000USD/a的固定投资费用会对换热器的生成和消去形成阻碍，增加网络中整型变量变异的难度。因此，在不改变问题节点数的前提下，根据流股的热容流率对其进行智能化调整，可有效避免一些无效的配置，从根本上减缓差解结构对优化进程的阻碍程度，减少算法在排除较差结果过程中浪费的计算时间，实现优化结果和效率的双重提升。

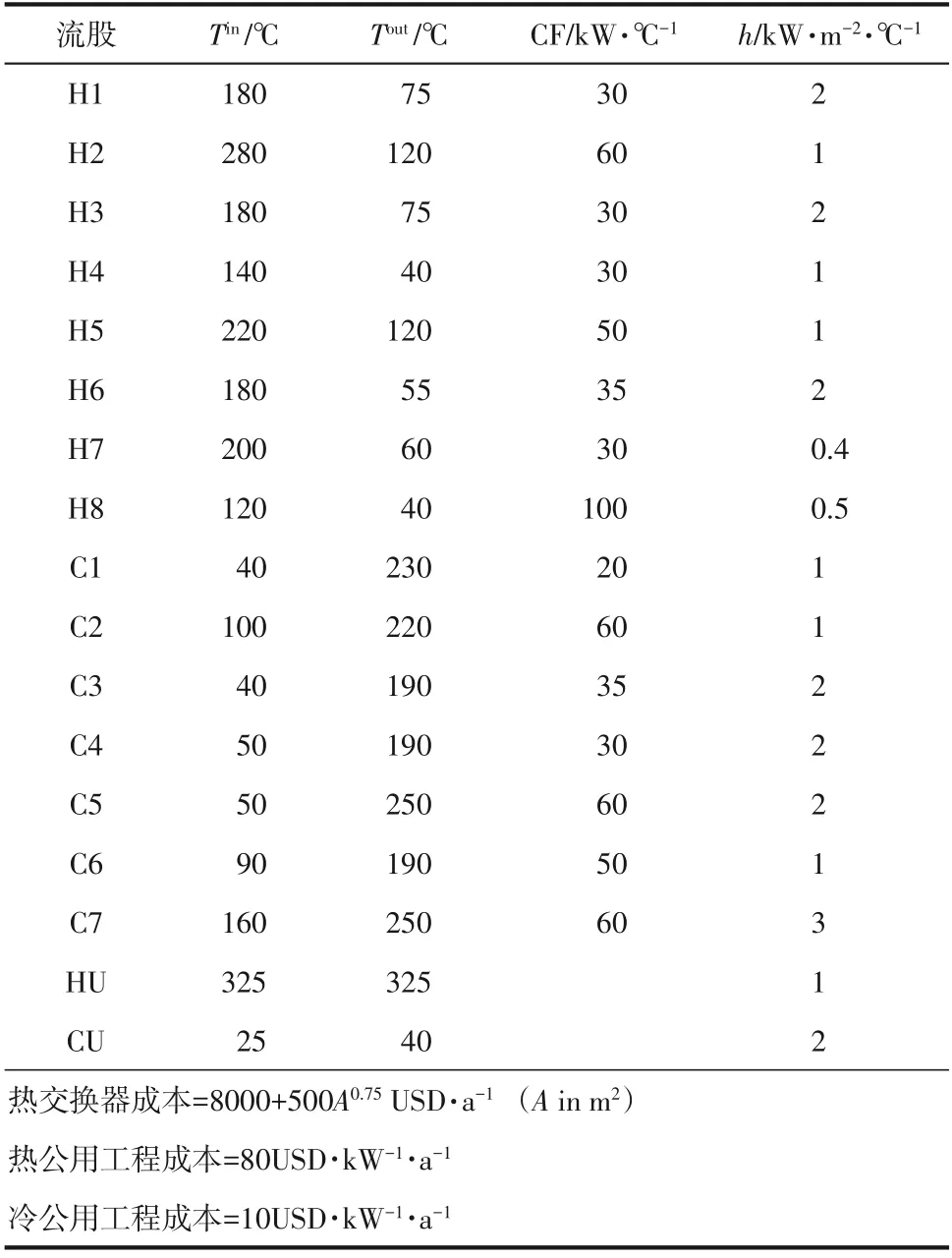
表5 15SP算例参数

NNM-AS 模型优化15SP 算例时，节点参数为NdH=5，NfH=3，NdC=4，NfC=4，MbH=MbC=2。经调整各流股的分流组数和分支数见表6。从表6 中数据可以得知H1、H3、H4、H5、H6、H7、C3、C4上出现了有分流和无分流两种配置关系，这种在同一股流股上实现两种模式的配置打破了有分流模型中对于结构的定式配置，更突显了NNM 模型“非结构”的特性。

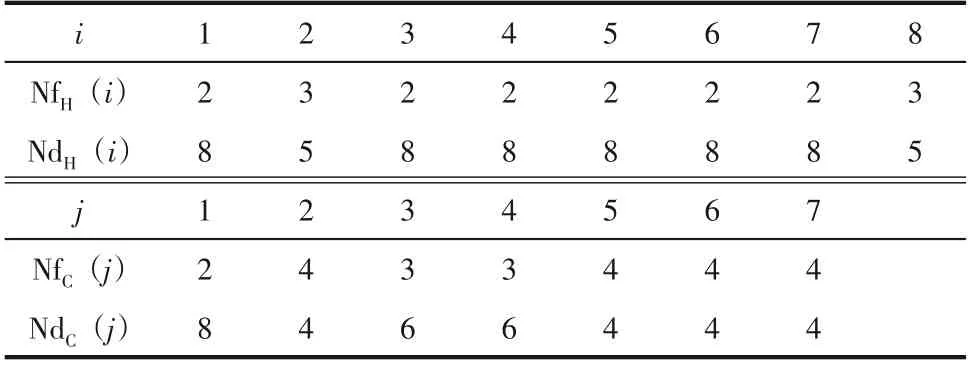
表6 NNM-AS模型中15SP算例各流股节点配置

应用RWCE 算法和NNM-AS 模型优化15SP 算例得到的费用及结构如图6所示。

图6 中TAC=1492628USD/a，根据表7 中结果对比，图6 中结果较目前文献中最优结果低2285USD/a。与徐玥等[31]的结果对比可发现，图6在H5C6上生成了一个换热器，通过对部分换热器换热量的调节，使得C2、C3 流股上无需外加公用工程，因此换热单元数相较文献[31]少1 个，进而降低了费用。在同参数下相同迭代步数内，采用NNM 模型优化15SP 算例，结果为1514066USD/a，佐证了在网络中多种节点配置对获取较优结果的重要性。

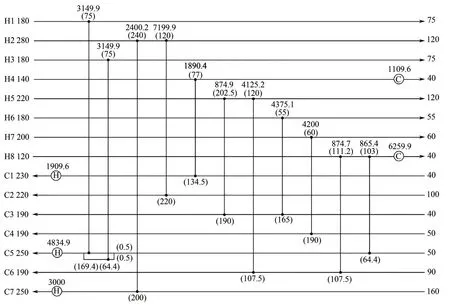
图6 采用NNM-AS优化15SP算例结果（TAC=1492628USD·a-1）

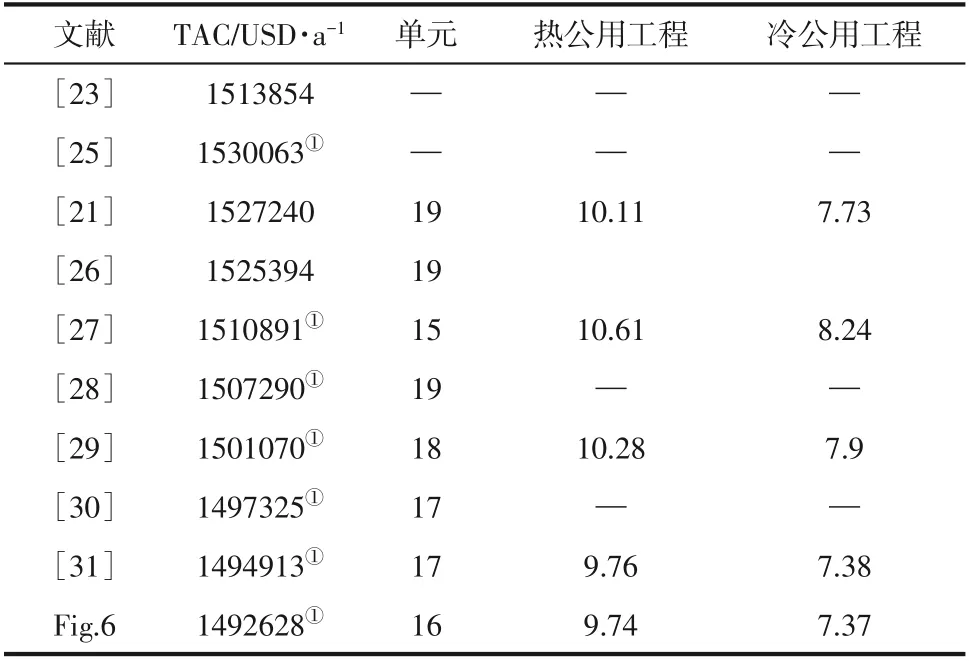
表7 15SP结果对比

5 结论

在分析NNM 模型的节点参数对网络配置及优化结果的影响时发现，有分流网络中不同流股对于分流的需求不同，且分流在热容流率较大的流股上出现的概率较大，因此提出了节点配置策略用以提升NNM 模型优化能力。该策略可根据各流股的热容流率调节其分流数与分流组数，使得热容流率较大的流股上分流数较多而热容流率较小的流股上分流组数较多。NNM-AS模型可对优势结构的产生起到引导作用，减少了无效分流结构对优化进程的制约，缩短了获取优质结果所需的时间。应用NNMAS模型和RWCE算法优化10SP和15SP算例，其结果分别比目前已有文献中最优结果低340USD/a 和2285USD/a，且质量和效率均优于同参数下NNM与RWCE算法所得结果。

符号说明

A—— 换热单元面积，m2

CA—— 面积费用系数，USD/(m2·a)

CF—— 热容流率，kW/℃

CU—— 冷公用工程

Ffix—— 固定投资费用，USD/a

HU—— 热公用工程

MbC—— 冷流股上分支上串联节点数

MbH—— 热流股上分支上串联节点数

NC—— 冷流股数目

NeNC—— 单股冷流股上的节点总数

NeNH—— 单股热流股上的节点总数