利用落球法开展几种食用油黏度的实验研究

郝星宇， 俞艳蓉， 高永伟

(宁夏大学 物理与电子电气工程学院，宁夏 银川 750021)

动力学黏度是液体的重要参数，在物理、化学、生物、医学等领域有重要应用.液体动力学黏度的测量一般采用旋转法、毛细管法、落球法等方法[1].落球法是较早被应用于液体黏滞系数测定的实验[2].由于该方法简单易行而被广泛使用.小球下落速度的确定是落球法测定液体动力学黏度的一个重要环节.传统的做法是采用秒表测量时间并进而计算得到，其误差较大.智能手机连拍功能的出现，也为进一步准确测量小球下降速度提供了可能.

为此，本文拟采用落球法并结合智能手机的连拍功能，测量并给出不同实验条件下常见几种食用油的动力学黏度，以分析量筒大小、小球直径对结果的影响，以及落球法在常见几种食用油黏滞系数测量中的适用性.

1 实验原理

在液体中缓慢下落的小球同时受到重力、浮力和黏滞阻力的作用.由于小球在液体中下落速度很慢，与容器直径相比小球半径很小，可将液体看作各方向均无限广阔，则斯托克斯公式可表达为

F=6πμvr，

(1)

式中：F为小球受到液体的黏滞阻力；v为小球下落速度；r为小球半径；μ为液体的动力学黏度，在SI制中，μ的单位为Pa·s.

小球刚进入液体时，重力大于黏滞阻力与浮力之和，小球作加速运动.随着小球运动速度的增加，黏滞阻力随之增加，故物体做加速度减小的加速运动，当加速度减小为0时，此时速度达到最大.设此时速度为v0，则小球受到的合外力为0，即

mg=6πμrv0+ρ0Vg.

(2)

之后，小球匀速下降，此速度称为终端沉降速度.于是，液体的动力学黏度可表达为

(3)

式中：ρ0为液体的密度；V为小球体积；g为重力加速度.实际上，小球被限制在容器内的液体中下降，液体在各个方向均为无限广阔的这一假设并不成立.故必须考虑容器的几何因素对小球运动状态的影响，两者相差一个修正因子β，密立根通过实验得到的修正因子如下式所示[3]

,

(4)

式中：2R为量筒的内径；h为液面的高度.于是，(3)式被修正为

μ1=μ/β.

(5)

由于斯托克斯公式是在假设流体无涡流的条件下推导得出的，也即小球下落时液体的状态并非如此理想.因此，还需要考虑液体状态对结果的影响，通过进一步修正给出的公式为

(6)

式中，Re为雷诺数，其定义为

.

(7)

与已有大多数通道内流体流动问题不同，这里考虑的是低雷诺数的绕流问题，故2r应为小球的直径.

2 实验仪器

与实验室条件不同，居家条件下开展常见液体动力学黏度的测定，仪器准备是完成该实验研究非常重要的一个环节.经过详细调研和认真准备，得到了实验需要的所有仪器和工具(表1).同时，图1更加直观地给出了实验仪器和测量工具.

在事业单位日常管理实践中，科学的人事档案能够真实记录事业单位广大职工的履历，能够全面记录事业单位的人事变革与发展，能够全面反馈事业单位的人才水平与质量。可以说，人事档案管理是事业单位各项管理的关键所在，因而我们需要全面优化事业单位人事档案的管理效益，综合性推动事业单位各项工作的稳步开展。

表1 实验仪器和测量工具

图1 实验所用主要材料图

3 实验测量

采用落球法测定液体的动力学黏度实验，关键的物理量是小球的下落速度.与传统的测量方法不同，本研究利用手机的连拍功能，通过捕捉相等时间间隔内小钢球位置的变化情况，能有效给出小钢球下落过程中的速度分布特征.在此基础上，可以准确计算出液体的动力学黏度.

本研究选用iphone 8 plus智能手机进行拍摄，该手机在连拍功能下，每秒拍摄10张静态连续照片，其任意相邻的两张照片的时间间隔为0.1 s.实验操作步骤见表2.

表2 实验操作步骤

按照上述操作步骤，即可确定小球在相邻0.1 s时间间隔内位置坐标，从而可确定小球的下落速度.图2给出了小钢球在蓖麻油中运动的过程.

图2 小钢球在蓖麻油中的运动过程

4 结果和讨论

一般情况下，为确定小球下落的终端沉降速度，会在圆筒内液面下方大约100 mm和筒底上方大约100 mm处分别做标记，测量两点间距离.在本实验中，液面的高度为450 mm，因此选取小钢球在350 mm以下的第1张照片作为计时起点，选取小钢球在100 mm以上的第1张照片作为计时终点，测量两点间的距离，记为l.记录计时起点和计时终点之间照片的数量确定小球运动的时间，记为t.所在地区重力加速度9.832 m/s2[4].

4.1 容器内径对小球速度的影响

(5)式已经表明，在不同的容器中小球下落的速度是有差异的，但人们对于此结论的理解存在一定的局限性.借助自制实验仪器研究不同容器中小球的下降规律，对于更好地理解斯托克斯定律，同时掌握容器内径对小球终端沉降速度的影响规律有重要意义.在内径为8.3 mm和79.5 mm的容器中分别进行黏度测量实验，用小球在匀速下落阶段的位移与其所用的时间相比得到v，然后将计算出的v依次带入 (3),(5),(6)式,得到液体的动力学黏度μ以及一次修正结果μ1和二次修正结果μ2，所得结果见表3.

表3 容器内径对小球下落速度及测量结果的影响

由(4)式和 (5) 式可知，小球在容器中的终端沉降速度比在广延液体中的终端沉降速度小，且容器直径越小，其差值越大，两者相差一个修正因子β.设内径分别为8.3 mm和79.5 mm的容器的修正因子分别为β1和β2，则由 (4) 式可得

经简单的计算可以发现，β1和β2的前一项分别为86.7%和9.1%，后一项均为0.3%.由此可见，实验仪器对结果的影响只需考虑内径大小即可.表3的结果表明，小钢球在内径分别为8.3 mm和79.5 mm的容器中下落的终端平均速度分别为27.77 mm/s和44.44 mm/s，这就说明对于直径相同的小球，容器内径越大，修正因子β越小，小球的终端沉降速度越大.

根据已有关于液体动力学黏度的拟合公式μ=5.529 2exp(-0.085 390T)[5]，可以计算得到在25.3 ℃下蓖麻油黏度的标准值为0.637 4 Pa·s.据此可以看出，采用内径较小的量筒(2R= 8.3 mm)测量并计算得到的动力学黏度，其未修正值，即μ大于标准值，但通过两次修正后的结果更接近标准值；对于内径较大的量筒，即2R= 79.5 mm，尽管修正前后结果变化并不明显，但二次修正值与标准值吻合更好.

4.2 小球直径对液体黏度的影响

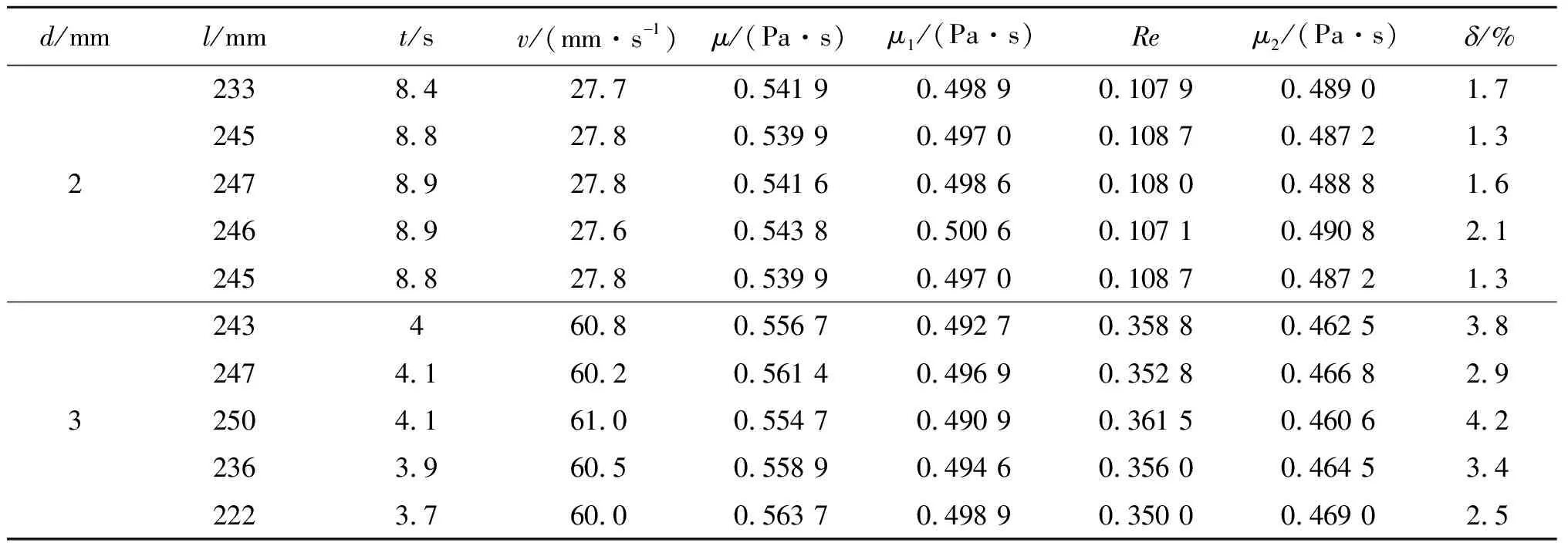
表4 利用两种不同小球测定蓖麻油黏滞系数的数据

由黏度拟合公式μ=5.529 2exp(-0.085 390T)[5]

可得温度为28.6 ℃时，蓖麻油黏度的标准值为0.480 9 Pa·s.考虑两个容器的几何效应对小球运动状态影响后所得到的μ1与蓖麻油黏度的标准值比较吻合，再进行二次修正，由表4得蓖麻油黏滞系数μ2与标准值的相对误差范围为-4.2%～2.1%.

同时，表4也表明，小球的直径越小，结果越准确.这是因为小球越大，下降速度增大，其惯性效应更加明显，进而雷诺数增大，这就导致流动的不确定性程度升高.小球下落速度的增加也引入了较大的测量误差.

4.3 落球法测定几种食用油黏度的适用性研究

利用落球法对常见的几种食用油，即大豆油、菜籽油及胡麻油的动力学黏度进行测定，测量数据见表5.

表5 3种不同液体动力学黏度的测定

上述3种液体作为中国家庭中常见的食用油类,都是脂类混合物，没有黏度的标准值，其黏度受种子品质、制备工艺等的影响较大.特里顿指出[6]：当雷诺数远小于1时，黏滞力大大超过惯性力，从而使得后者在流体力学方面所起的作用可忽略不计.当雷诺数Re> 5时，惯性力与黏性力相近，不适宜用落球法测液体的黏滞系数.由表5可知，钢球在大豆油、菜籽油、胡麻油中的运动时雷诺数的平均值分别为14.371 3,11.666 0,14.647 2，其雷诺数均大于5.这即说明利用落球法测量上述几种常见食用油的黏度存在一定的局限性.

事实上，当雷诺数增加时，常用计算公式，即 (6)式已不能准确反映流体运动状态对测量结果的影响，应考虑更高阶级数展开项.同时，保持量筒和液体不变时，雷诺数的增加反映了液体流速的增大，进而导致斯托克斯公式并不成立.于是，采用落球法测定液体动力学黏度的理论将不再成立.

由此可见，尽管除常见的蓖麻油外，采用落球法测量大豆油、菜籽油及胡麻油的动力学黏度存在一定的局限性，但上述测量结果仍可为了解几种食用油的黏滞特征提供参考，并为采用其他方法测量动力学黏度提供借鉴.

5 结语

以常见几种食用油为研究对象，基于落球法并采用多种实验测量手段，测定了不同条件下食用油的动力学黏度，得到如下结论：

1)液面高度相同时，量筒越粗，钢球下落速度越慢;量筒越细，尽管初次测量值与标准值误差较大，但二次修正结果与标准值吻合很好.同时，量筒越粗，初次测量值与修正值差异并不明显，但修正结果与标准值更加接近.

2)研究小球直径对液体动力学黏度结果影响的实验表明，由于小球直径越小，其惯性效应远小于液体对钢球产生的斯托克斯黏滞阻力影响，运动过程中越能体现液体的黏滞特征，故小球越小，结果越准确.

3)采用落球法测定几种食用油动力学黏度的结果表明，由于小球在菜籽油、大豆油和胡麻油等液体中下落时雷诺数大于5，导致落球法测量此类液体中下落时雷诺数大于5，导致落球法测量此类液体动力学黏度时存在一定的局限性.但测量结果仍能为了解几类食用油的黏滞特征提供参考，并为其他实验方法测量结果提供借鉴.