关于带有有向图的G -非扩张映射的有限步SP-迭代方法的收敛性分析

贾倩倩, 高兴慧

(延安大学 数学与计算机科学学院，陕西 延安 716000)

不动点理论将各种非线性问题转化为寻求某个映射的不动点问题加以解决，在理论和应用中起着至关重要的作用，其中最著名的是度量不动点理论中的Banach压缩原理.后来许多学者在不同方向上扩展和推广了不动点理论(文献[1—3])，特别地，Jachymski在文献[4—5]中将不动点理论与图论中的概念结合起来，在具有有向图的完备度量空间中推广了Banach压缩原理.之后，许多学者对在具有有向图的Banach空间上的不动点问题进行了研究，并给出了相关结论(文献[6—7]).Phikul Sridarat在文献[8]中给出了关于3个G-非扩张映射的公共不动点的三步SP-迭代方法，迭代算法如下：

(1)

受上述工作的启发，本文给出了有限个G-非扩张映射的公共不动点的有限步SP-迭代的强收敛定理和弱收敛定理，并给出数值例子论证该方法的优点，算法如下：

(2)

1 预备知识

定义1[9]称T:C→C为G-非扩张的，若T满足下列条件：

(ⅰ)T保留G的边界，即(x,y)∈E(G)⟹(Tx,Ty)∈E(G)；

(ⅱ)T不增加G的边权值，方式如下:

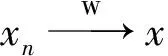
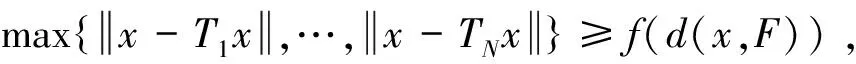
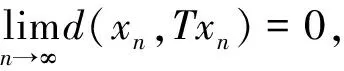
定义6[11]设C是赋范空间X的非空子集且G=(V(G),E(G))是有向图,满足V(G)=C,称C有性质G:若C中的每个序列弱收敛于x∈C且(xn,xn+1)∈E(G)，对所有的n∈N，则存在{xn}的子序列{xnj}使得(xnj,x)∈E(G),∀j∈N.

注1[11]若G是可传递的，则性质G等价于若C中的序列{xn}满足(xn,xn+1)∈E(G)，使得对{xn}的任一子序列{xnj}弱收敛于x∈X,则(xn,x)∈E(G)，∀n∈N.

2 主要结果

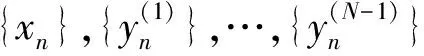
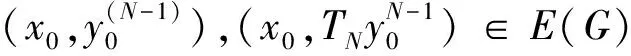
证明因为

(3)

并且

(4)

综上所述可得

(5)

于是

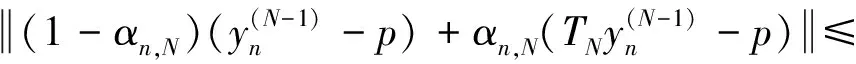
(6)

那么

(7)

(8)

由xn+1的定义可得

(9)

(10)

(11)

从而

(12)

(13)

(14)

因为

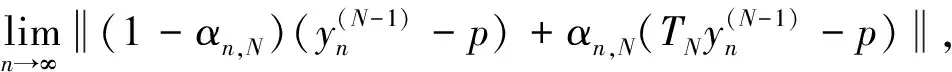
(15)

由(14)～ (15)式及文献[6]中的引理2.1可得

(16)

(17)

(18)

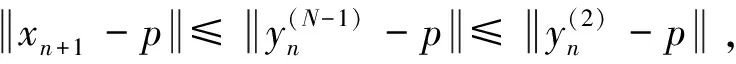
(19)

由(17)式和(19)式得

(20)

(21)

(22)

又

(23)

在(23)式两边取极限，由(21)～(22)式得

(24)

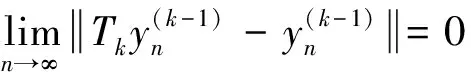
(25)

(26)

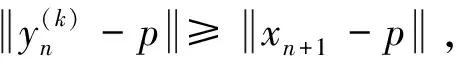
(27)

由(25)式和(27)式得

(28)

(29)

故

证毕

主导的，则{xn}弱收敛于x∈F.

引理3的证明过程类似于文献[6]中引理3.8的证明.

主导的，则{xn}强收敛于x∈F.

3 数值实验

在这一节中，我们给出了数值实验用于支持所得到的重要定理.

例1设X=R且C=[0,2],假设G=(V(G),E(G))是有向图且满足V(G)=C，(x,y)∈E(G)当且仅当0.50≤x≤y≤1.70，T1,T2,…,TN定义如下：

在相同的迭代步数下比较SP-迭代和多步Noor-迭代收敛速度(图1～2).

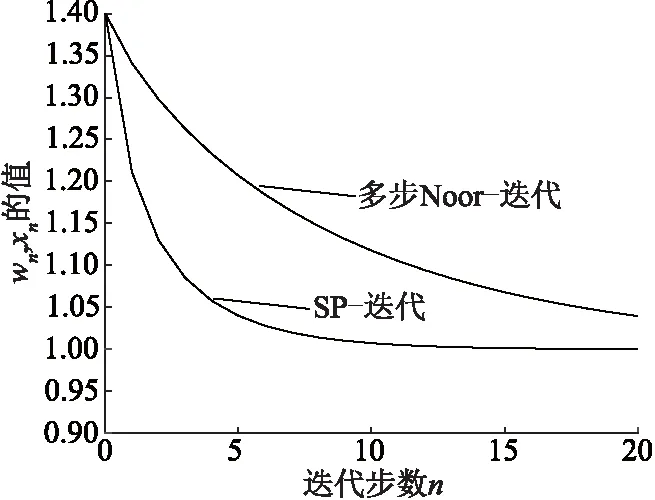
图1 迭代图

由迭代图可知在相同迭代步数和初始值下SP-迭代收敛于1的速度明显快于多步Noor-迭代.

4 总结

本文介绍了有限个G-非扩张映射的SP-迭代方法，并在带有有向图的一致凸的Banach空间中证明了其强收敛定理和弱收敛定理，并给出数值例子比较其与多步Noor-迭代的收敛速度，得到该方法收敛的优越性.

图2 误差图