面向未知目标的柔性关节空间机器人滑模控制

张文辉， 陈浩文， 闻 志， 叶晓平

1. 南京晓庄学院电子工程学院, 江苏 南京 211100 2. 南京工程学院, 江苏 南京 211100 3. 浙江理工大学机械与自动控制学院， 浙江 杭州 310000 4. 浙江省航空航天金属导管塑性成形技术与装备重点实验室， 浙江 丽水 323000 5. 丽水学院工学院，浙江 丽水 323000

0 引 言

近半个世纪以来，机器人技术在空间探索中的应用越来越广泛[1-2].从前苏联“礼炮号”空间站到欧盟“国际空间站”，再到我国“天空一号”空间实验室，空间机器人已经被越来越广泛应用于空间站的建设与维护.其中最著名的为欧盟“国际空间站”加拿大Canadarm-2空间机械臂，该机械臂主要对航天器舱内和舱外不同目标进行拾取、搬运、定位和释放.同时，协助航天员完成在轨建设或维修.2010年，Canadarm-2空间机械臂成功捕获SpaceX龙飞船，实现了极低成本的空间载人往返.2019年5月加拿大航天局(CSA)宣布，将建设Canadarm-3空间机械臂项目，该机械臂采用碳纤维复合材料，具有轻质，高速的特点，相比较1代、2代机械臂，其关节柔性无疑更高.

关节柔性能够在空间机器人在抓捕目标载荷时，能吸收碰撞能量，避免损坏执行机构.但其柔性特性会造成机械臂末端产生残余振动和关节转角误差，影响系统稳定性和控制精度[3-5].因此，柔性机器人控制及振动抑制问题正逐渐成为国内外学者研究的热点[6-8].

当前，柔性机器人文献研究主要集中在固定基座的地面柔性机械臂[9-10]，偶有空间漂浮基柔性机器人的研究，也未考虑目标载荷的情况，更很少涉及面向未知非合作目标载荷的空间柔性机器人控制系统.空间机器人由于其基座的漂浮性，因此相对地面机器人具有更强的耦合性.且考虑到空间复杂的未知工况，非合作目标载荷的精确质量难以获得等问题，研究面向未知目标载荷捕获的空间柔性机器人控制与振动抑制具有重要意义.

1986年， MARINO等[11]首次对柔性关节机器人的非线性控制问题进行了研究，基于机器人动力学模型的奇异摄动和积分流形，提出了全局反馈线性化控制律和非线性复合控制律.1987年，SPONG[12]给出了柔性关节机器人的简化动力学模型，并对柔性关节机器人的位置控制问题进行了研究，通过反馈线性化将柔性关节机器人动力学方程进行解耦，将非线性系统转化为线性系统进行控制，分析了闭环控制系统的性能和鲁棒性.上述两位学者奠定了柔性机器人控制与振动抑制的研究基础，后续学者在此基础上进行了更加深入的研究.LI等[13]通过将输入整形技术和自适应参数自抗扰控制器相结合，解决了强干扰情况下的双关节柔性机械臂振动抑制问题，该方法不需要精确的数学模型，即使机械臂机构参数发生变化，也能保证系统的鲁棒性.ULRICH 等[14]研究了柔性关节空间机械臂的非线性自适应输出反馈控制问题.提出了一种基于分散自适应的复合控制方案，该方案在控制准稳态机器人模型的基础上，加入一个线性修正项来稳定边界层模型.陈力等[15]针对空间柔性机械臂协调运动，提出基于奇异摄动理论的鲁棒神经网络的PD振动抑制方法，采用神经网络来逼近慢变子系统的位置不确定模型，PD控制来实现快变子系统的振动抑制.这些研究成果虽然只针对合作目标，但为进一步深入研究非合作目标的柔性空间机器人控制提供了有价值的思想.

对于载荷捕获的漂浮基空间机器人控制问题，考虑到空间环境复杂未知工况导致的捕获目标质量未知问题，设计基于迭代的最小二乘法来辨识非合作目标质量.考虑空间机器人载体自由漂浮特性，采用拉格朗日方法和动量矩守恒原理建立漂浮基座柔性关节空间机器人动力学模型.考虑空间机械臂关节的柔性特性，基于奇异摄动理论将系统模型近似地分解为快慢变子系统进行分别控制.其中针对慢变子系统，设计滑模变结构控制器，保证控制的实时性和鲁棒性；针对快变子系统，设计基于速度差值的反馈补偿控制算法，抑制柔性关节产生的残余振动.

1 柔性关节空间机器人动力学建模

漂浮基柔性关节两连杆空间机器人如图1所示，其整体结构包括：空间机器人载体B0、刚性连杆(B1、B2)、柔性关节转动铰(O1、O2)与目标未知负载P.建模前作以下假设：

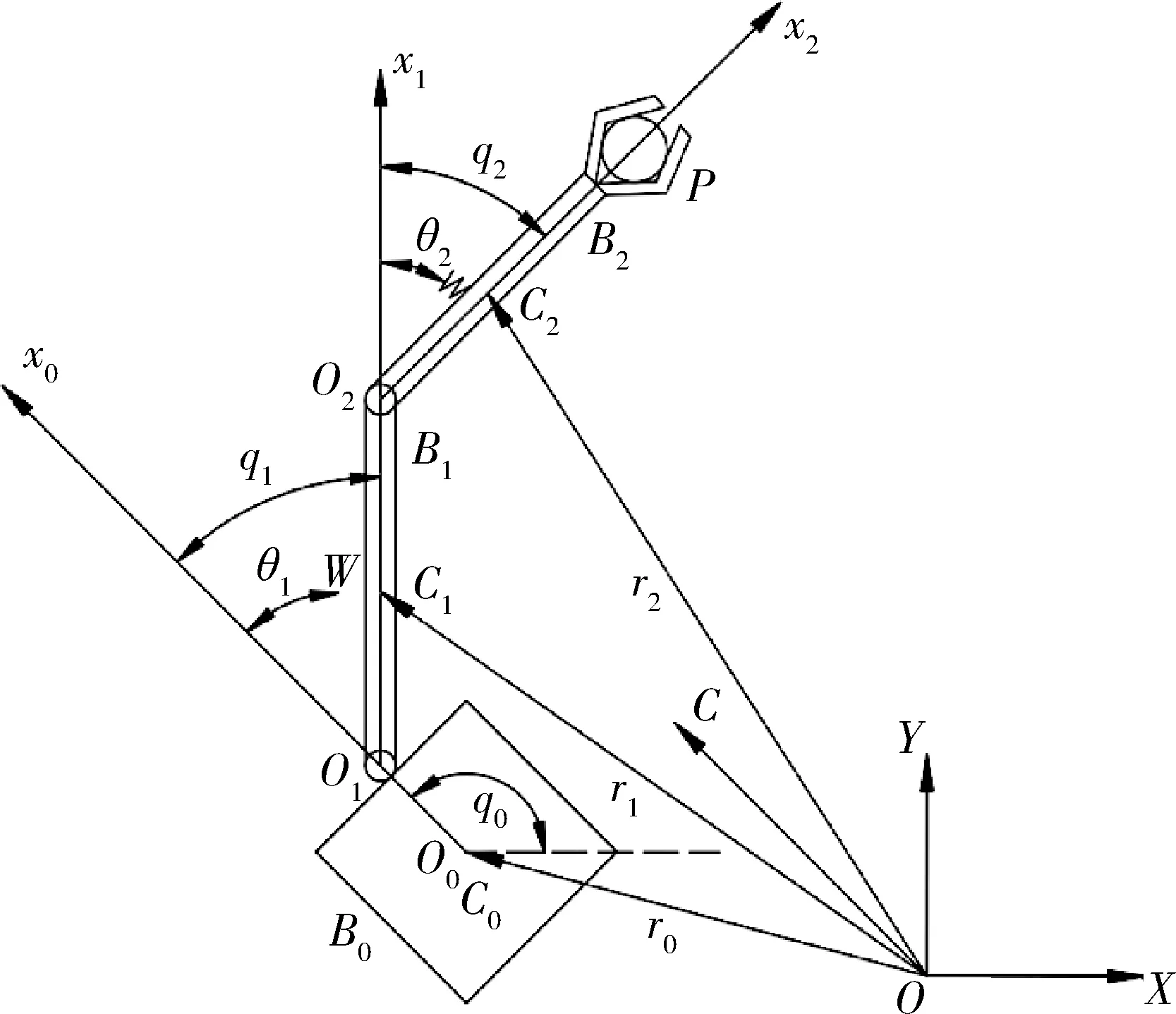
图1 漂浮基柔性关节空间机器人系统Fig.1 Floating flexible joint space robot system

假设1.漂浮基柔性关节空间机器人仅在OXY平面运动，忽略Z轴；

假设2.空间机器人臂杆及载体均为质量均匀、形状固定的刚体，其质心位于各自几何中心；

假设3.非合作目标载荷为简化为一质量未知的质点.

根据Spong关节模型简化原理[12],将柔性关节的变形近似等效为刚度系数为K的线性扭转弹簧，如图2所示的结构.当关节Oi(i=1,2)处的电机转子转动角度θi时，与其相连的刚性连杆Bi由于扭簧弹性力的作用，会产生相应的转动误差Δi，因此刚性连杆转动角度qi=θi+Δi.一般情况下，Δi≠0，若忽略关节柔性造成的传动误差，即假设θi=qi，则必然造成误差的不断累积，从而对控制精度和系统稳定性造成较大影响.

图2 柔性关节结构图Fig.2 Structure of flexible joint

由于空间柔性关节机器人处于自由漂浮状态，则系统遵守动量守恒和动量矩守恒.利用拉格朗日方程推得漂浮基柔性关节空间机器人的动力学方程如下：

(1)

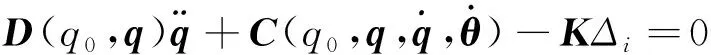
(2)

基于奇异摄动理论将系统近似地分解为表示弹性振动部分地快变子系统和表示刚性运动的慢变子系统，并分别设计快慢变子系统的独立控制算法.

总控制算法表示为：

τ=τs+τf

(3)

式中,τs为慢变子系统控制器.τf为快变子系统控制器.

设正定对角矩阵K1=ζ2K，其中ζ为一个非常小的正常数.定义弹性力z=K(θ-q)为快变量，则动力学方程近似分解为：

(4)

(5)

由上式K=K1/ζ2可知，当ζ→0时，K→∞，此时关节处可近似为刚性连接，即Δi=θi-qi=0，则慢变子系统动力学方程转换为

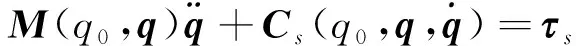
(6)

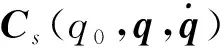
2 基于奇异摄动的振动抑制控制

基于奇异摄动理论和最小二乘法参数辨识，设计如下控制系统如图3所示.其中RLSM(recursive least square method)为递推最小二乘法，SMC(sliding mode controller)为滑模变结构控制器，SDC(speed difference controller)为速度差值控制器.

图3 控制系统原理图Fig.3 Schematic diagram of control system

2.1 非合作目标的质量观测器设计

考虑空间非合作目标质量的不确定性，将动力学方程中的矩阵模型表示为两部分：

(7)

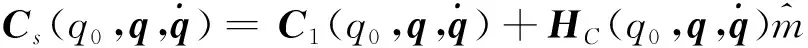
(8)

将式(7)～(8)代入慢变子系统动力学方程(3)得

(9)

式中,

(10)

2.2 快变子系统控制器设计

针对快变子系统，设计基于速度差值的反馈控制器

(11)

将式(3)和式(11)代入式(4)，则快变子系统动力学方程为

(12)

2.3 慢变子系统控制器设计

将式(6)整理得

(13)

其中

则设计双曲正切滑模变结构控制器为

(14)

这里式(14)中具有以下性质：

3 控制系统稳定性分析

定理.针对柔性机器人系统方程(1)～(2)中的慢变子系统(6)，采用滑模变结构控制器 (14)，能够保证控制系统的稳定性.

证明. 定义Lyapunov函数

(15)

对V进行求导

(16)

由于

(17)

将式(14)和(17)代入式(16)中，得

从而

下面的证明用到了如下性质：

则：

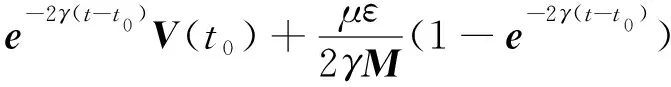
(18)

4 仿真研究

如图4所示为双关节漂浮基柔性关节空间机器人，以此模型为被控对象，利用本文设计的混合控制算法进行数值仿真实验.

图4 漂浮基柔性关节空间机器人Fig.4 Floating flexible joint space robot

表1 柔性关节空间机器人参数Tab.1 Parameters of flexible joint space robot

其中，基座质心C0与关节O1的距离为0.5 m，杆B1、B2的质心分别位于连杆的中间位置，电机转子的转动惯量矩Jθ1、Jθ2均为0.33 kg·m2.假设空间机器人关节角运动的期望轨迹为

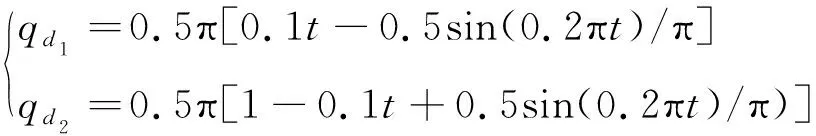
设初始值为q(0)=[0.2 1.4]Trad、θ(0)=[0.2 1.4]Τrad.Kf=diag{0.17,0.17}，Kp=diag{3 000, 3 000}，Kd=diag{300,300}，Λ=diag{0.5,0.5}，γ=10，ε=0.03.

4.1 非合作目标质量观测器数值仿真

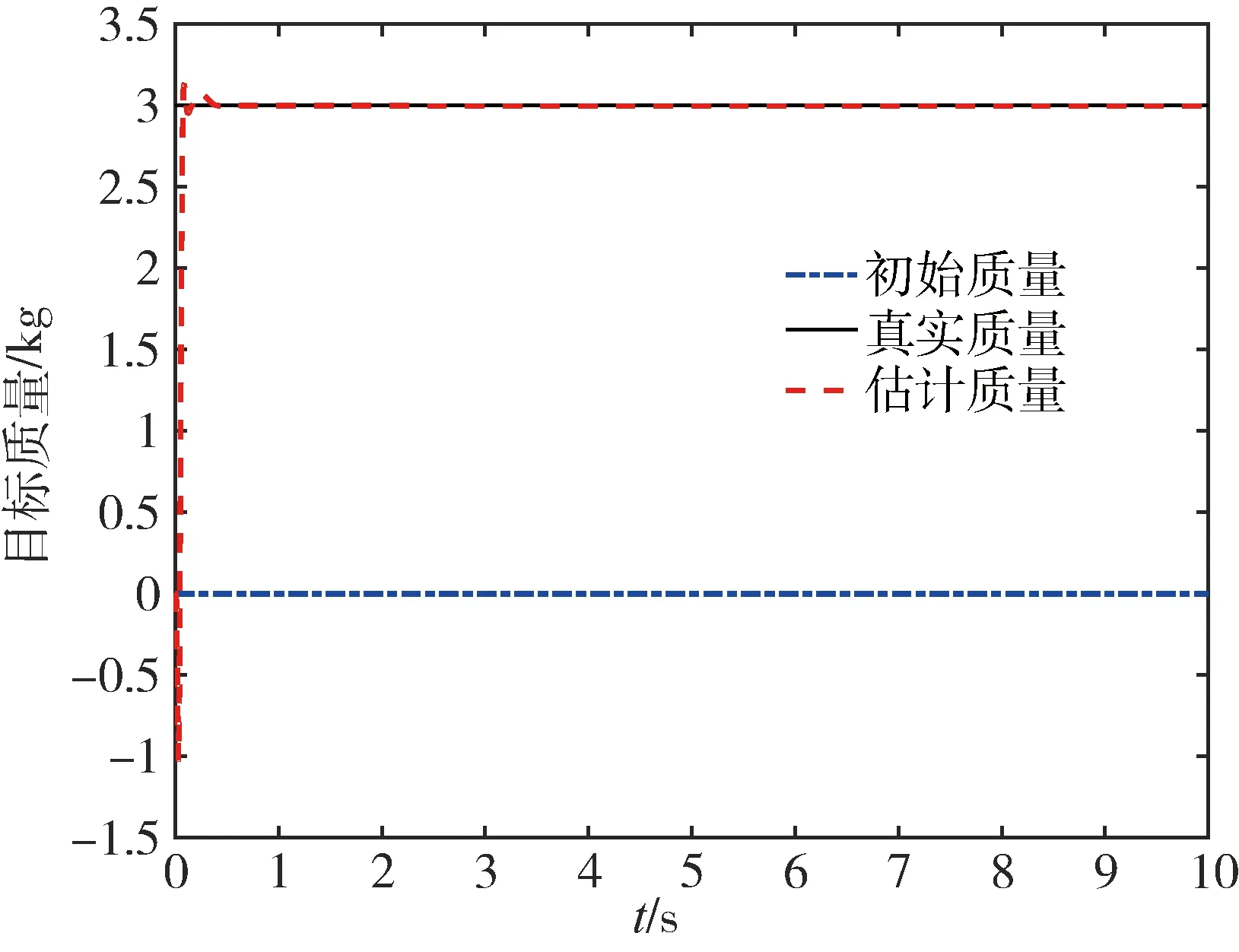
图5 非合作目标质量的估算Fig.5 Estimation of non-cooperative target quality

从图5中可以看出，非合作目标初始值设定为0，所以在初始阶段误差较大，但经过0.2 s后，估算值接近实际值，估计误差大约为5.0%.当达到0.5 s后，从图中可以看出估计值和实际值基本重合，采用改进的最小二乘算法设计的质量观测器基本能够很好的获得真实的非合作目标质量.在初始阶段出现较大超调的主要原因在于电机转子转动的角度、角速度与连杆转动的角度、角速度在运动初始阶段都很小，含有质量等不确定因素部分Φ≈0，对非合作目标质量的估算值近似奇异，造成初始误差较大.

4.2 基于奇异摄动的混合振动抑制控制

针对非合作目标捕获的柔性关节空间机器人，基于奇异摄动理论的快变子系统采用速度差值控制器，慢变子系统分别采用滑模控制(SMC)和PD控制进行比较分析.控制效果如图6～图10所示.图6为柔性关节空间机器人各连杆转角期望轨迹与实际运动轨迹对比图，图7为电机转子转角的期望轨迹与实际轨迹的对比图，图8为两关节处电机输出力矩对比图，图9为关节处臂杆转角和电机转子转角差值图，图10为漂浮基体的轨迹对比图.

图6 连杆转角轨迹跟踪Fig.6 Trajectory tracking of space robot link angle

图7 电机转子转角轨迹跟踪Fig.7 Trajectory tracking of motor rotor angle

图8 关节处力矩的输入Fig.8 Joints torque input

图9 关节处相对误差Fig.9 Relative errors at joints

图10 自由漂浮基体位姿Fig.10 Free floating body poses

从图6～ 7中可以看出，针对未知非合作目标捕获问题，两种控制系统均在0.2 s时产生较大超调量，但SMC控制能够更快的抑制残余振动，由图中可以看出，在0.5 s内快速准确跟踪到期望轨迹，获得较好的控制效果.而采用PD控制时，臂杆关节角度产生的超调相比SMC更大，在超过2 s后跟踪误差才逐渐变小，且无法精确跟随期望轨迹，依然存在一定的误差波动.由图8可知，臂杆转角和电机转子转角差值在1 s内均接近0，表明弹性形变造成的误差已经消除，其中采用SMC控制误差更小.由图9可知，两种控制方法的控制力矩均不大，其中SMC为了保证控制系统鲁棒性，初始输出力矩更大，但迅速稳定，波动更小.采用PD控制，其输出力矩具有一定波动，但不大.由图10可以看出，空间机器人漂浮基座依然能够保持期望位姿姿态，具有较好的鲁棒性.

通过仿真对比说明了采用奇异摄动理论的SMC控制或PD控制均能够获得不错的控制效果.但SMC控制算法相比PD控制能够更好的消除弹性振动，获得更高控制精度.

4.3 关闭快变控制τf，采用独立SMC控制

当关闭快变控制器τf时，相当于采用独立SMC控制，其控制效果见图11～15.

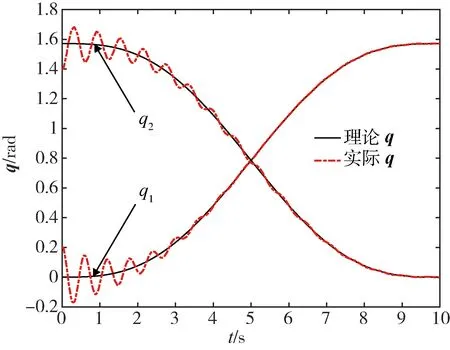
图11 空间机器人连杆转角轨迹跟踪Fig.11 Trajectory tracking of space robot link angle

由图11可以看出，关节角度在6s内都无法达到较好轨迹跟踪，且控制阶段前期误差较大.由图12可知，电机转子转角在初始阶段产生了较大振荡，并在后期一直伴随一定误差.由图13可知，采用独立SMC控制所输出的控制力矩较大，且存在一定抖动，这会对执行器造成损害.从图14可以看出，臂杆转角和电机转子转角差值始终存在，最大达到了0.3 rad，这表明弹性形变造成的误差没有消除.由图15中可以看出，采用独立SMC控制，漂浮基的位置与姿态均受到了较大影响，在Y轴方向上最大产生了8 m的偏移，控制效果不佳.

图12 电机转子转角轨迹跟踪Fig.12 Trajectory tracking of motor rotor angle

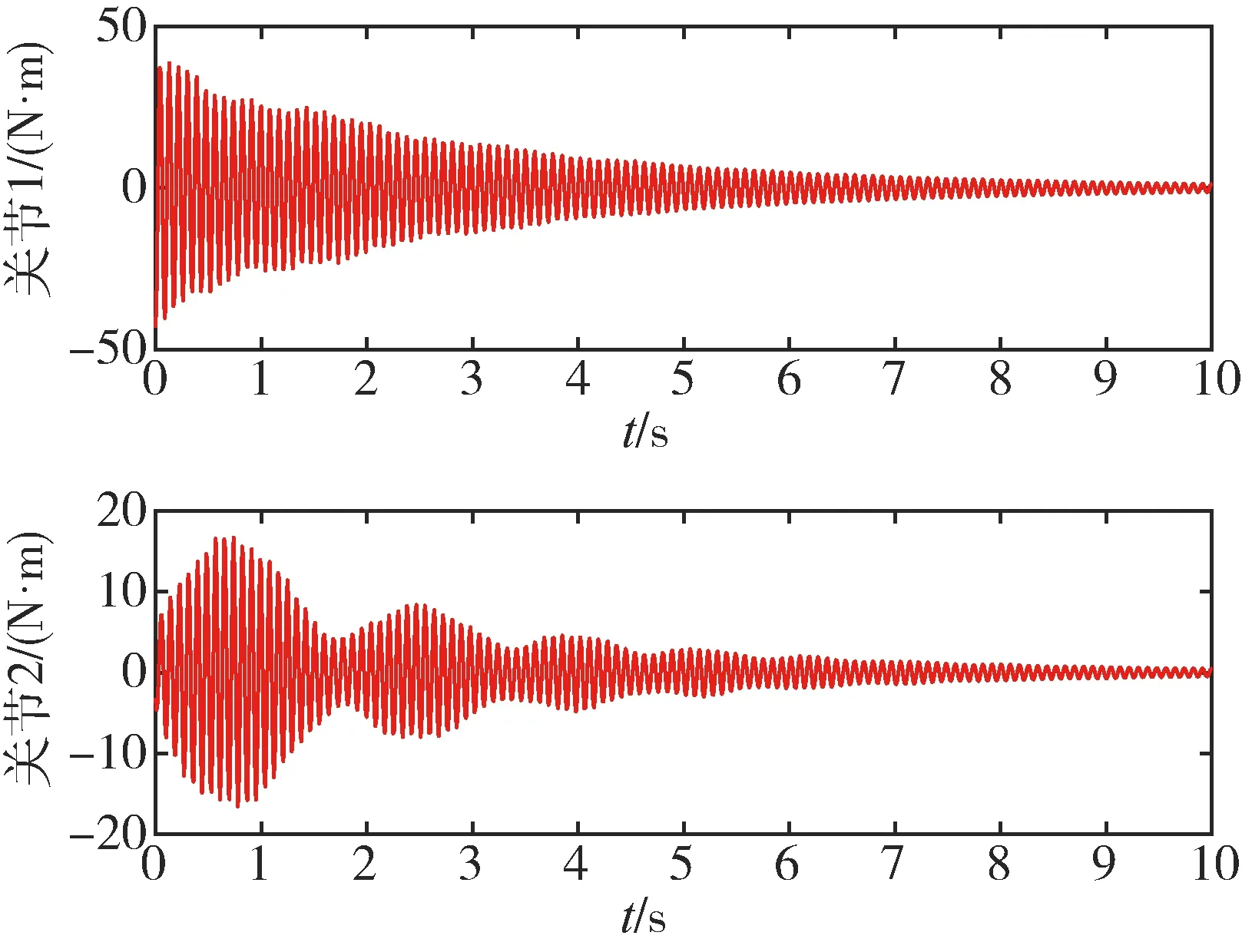
图13 关节处力矩的输入Fig.13 Joints torque inputs

图14 关节处相对误差Fig.14 Relative errors at joints

图15 自由漂浮基体位姿Fig.15 Free floating body poses

通过仿真分析可以看出，采用独立SMC控制难以取得较好控制效果.而基于奇异摄动理论实现对快慢变子系统的混合控制能够获得更好控制效果，同时证明所设计的基于速度差值的控制器对于柔性关节机器人振动抑制是有效的.

5 结 论

针对非合作目标的柔性关节空间机器人控制问题，提出了一种基于质量观测器的滑模变结构控制方法.

(1)考虑到空间非合作目标质量的未知性，设计了基于改进的最小二乘法质量观测器，实现了非合作目标的质量辨识.

(2) 基于奇异摄动理论将系统动力学模型近似地分解为快慢变子系统.针对慢变子系统，设计了滑模变结构控制器，保证了控制精度；针对快变子系统，设计了基于速度差值的反馈补偿控制器，抑制了柔性关节产生的残余振动，提高了系统鲁棒性.

(3)通过仿真实验揭示了快变子系统对于柔性环节振动抑制的作用机理，慢变子系统对于刚性部分的轨迹跟踪作用机理.实验同时验证了SMC控制相比PD控制更优，基于奇异摄动理论的混合控制相比独立SMC控制效果更佳.