基于人工势场的星群松散编队控制

高婉莹， 李克行

1. 北京控制工程研究所, 北京 100094 2. 空间智能控制技术重点实验室, 北京 100094

0 引 言

20世纪80年代以来，随着高新技术的发展以及航天任务需求的不断扩大，卫星研制逐渐向小型化、低成本方向发展[1],并于20世纪末出现了微纳卫星的研究热潮.利用低成本的微纳卫星组成大规模集群协同工作，可以完成更为复杂的空间任务，成为当今世界航天大国重点关注的战略发展方向.

星群与传统编队飞行都是为了完成某项空间飞行任务的多颗卫星集合，但它们之间存在明显差异.传统编队飞行多采用集中式控制方法使得各颗卫星保持严格的空间构型，容错性较差、灵活性不强，而且控制器设计比较复杂.星群一般规模更大，强调以局部信息交互保持集群整体有界[2-3].由于存在轨道摄动等因素影响，大规模星群如果维持精确的空间构型将产生巨大的能量消耗.在某些集群任务中，星群的几何构型不会影响最终任务结果，各颗卫星间只需要保持松散有界即可[4].

星群松散编队控制技术允许星群中各成员间相对距离在一定范围内波动，其控制要求仅为各颗卫星相对运动有界，主要体现“松散”的特征.以人工势场法为代表的分布式控制方法可以充分考虑集群内部各成员之间的协同关系，实现整个集群的信息共享与协同合作，可以增强系统可靠性，达到更好的控制效果，完成更复杂的空间任务[5].

人工势场法是KHATIB提出的[6]，该方法早期应用于机器人编队中的路径规划和避障问题，其控制原理是根据被控对象的周围环境构建人工势场，令被控对象的期望状态位于系统势场的全局最小值点，然后设定控制律，保证被控对象沿着势场的负梯度方向运动，直至收敛于期望状态.目前人工势场法已经在机器人[7]和无人机[8]领域应用取得了良好的效果，也逐渐开始应用于航天器在轨交会任务、在轨组装等方面的协同控制研究[9-15].比如LOPEZ等[11]结合人工势场法实现存在障碍物并且考虑最终交会方向的航天器会合控制；PINCIROLI等[12]基于Lennard-Jones势研究控制微纳卫星群在轨道上建立平面正六边形晶格构型，以便应用于大型航天器的在轨组装；曾志峰等[13]基于Tersoff-Brenner势使航天器群自发实现图形编队，在地球同步轨道上建立正四面体目标构型；RENEVEY等[14]将人工势场法与相对轨道元素相结合，使12颗卫星平均分布在同一虚拟中心的两个圆型相对轨道上.但是目前这些研究多偏向于传统精密编队，基本都属于星群任务构型控制，目前对大规模星群的松散编队运行模式研究较少.

在理想情况下，星群松散编队运行模式类似于自然界中的蜂群、鸟群等，以不碰撞、低能耗状态在轨运行.但由于卫星运行于特殊的太空环境，受到轨道动力学约束，并且还需要考虑微纳星群在执行机构和测量信息方面的约束.对空间任务而言，燃料消耗是控制系统设计时需要考虑的一大制约问题，由于对卫星进行轨道面外控制需要消耗大量的燃料，对星群进行控制不能直接照搬无人机、地面机器人等的控制方法.本文考虑星群轨道动力学约束，将人工势场法应用于卫星控制，并引入了基于相对运动动力学方程的速度反馈控制，可以有效建立并保持星群松散编队，同时实现星间避碰、集群空间避障，而且通过仿真算例验证了控制方法的可行性.

1 构造人工势场

人工势场与电磁学中的电场概念相仿，在人工势场法中，通过建立吸引势场和排斥势场，使目标点对星群中个体卫星产生引力，障碍物对卫星产生斥力，各颗卫星间也存在一定排斥作用，卫星在势场中的受力效果如图1所示.其中势场作用力的大小、方向和卫星与目标间、卫星与障碍物间、卫星与星群中其他卫星间相对状态有关，综合卫星在势场中所受合力，将其作为系统控制输入信息，对卫星速度进行调整，即可实现星群整体控制.

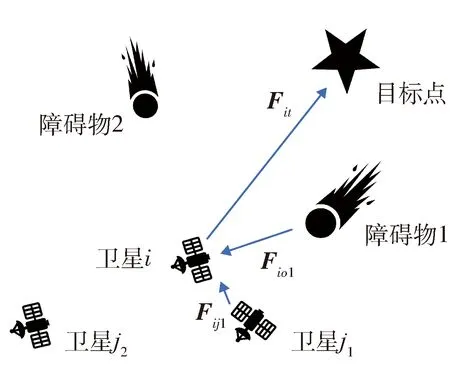
图1 卫星在势场中受力示意图Fig.1 The forces on the satellites in the potential field

1.1 目标吸引势场

吸引势场的作用是将卫星聚集在目标点位置，一般将目标位置设置为势场最低点，同时引力场的场强随着卫星与目标间距离的增大而增强.常见的抛物型吸引势场函数可表示为

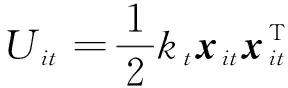
(1)

位于势场中的卫星i所受目标吸引力Fit为

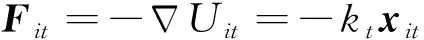
(2)

式中,kt是取正的控制参数，xit是卫星与目标之间的相对位置矢量.

式(2)中吸引力与相对距离成正比，当卫星离目标点较远时，计算得到的作用力将很大，考虑到微纳卫星存在推力限制，引入反正切函数对吸引势场进行改进，改进后的吸引势场函数可表示为

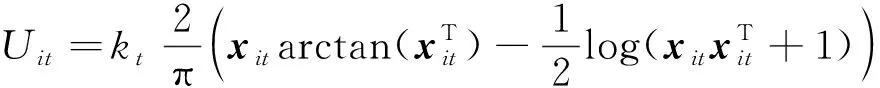
(3)

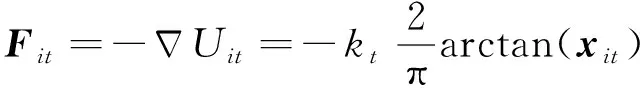
(4)

式(4)中吸引力为有界值，当卫星离目标点较远时，所受吸引力趋近阈值kt，从而保证卫星所受作用力在合理范围内.取参数kt=1，绘制目标吸引作用力曲线如图2(a).

1.2 星间避碰排斥势场

星间避碰排斥势场是基于星群内部各成员卫星间相对位置信息建立的，当星间距离小于安全值时卫星受到排斥作用，避免星间碰撞.通过引入一个光滑阶跃函数，对避碰势场的作用边界进行限制，当星间距离超出安全范围时，星间无作用力.这样设计一方面可以避免非临近航天器个体之间互相干扰，同时也符合实际应用中星群局部通信的特征.

构造避碰势场作用力Fij的具体形式如下：

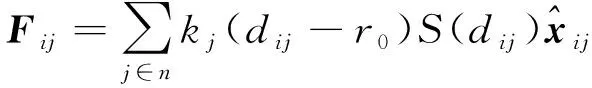
(5)

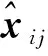
(6)

s(z)=0.5+0.562 5cosπz-0.062 5cos3πz

(7)

式中，r0是光滑阶跃函数的右边界，当星间距离大于r0时，卫星超出避碰势场的作用范围，某种意义上来说，r0即代表星间安全距离的上限.取参数kj=1，r0=50 m，绘制星间避碰排斥作用力曲线如图2(b).

1.3 空间避障排斥势场

空间避障排斥势场通过在障碍物所处位置设置较大的势场值，驱使星群及时躲避轨道上的其他航天器或空间碎片.基于高斯势场建立球型避障势场

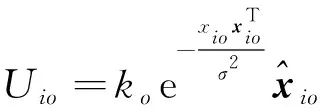
(8)

则障碍物附近的卫星i所受避障作用力Fio为

(9)

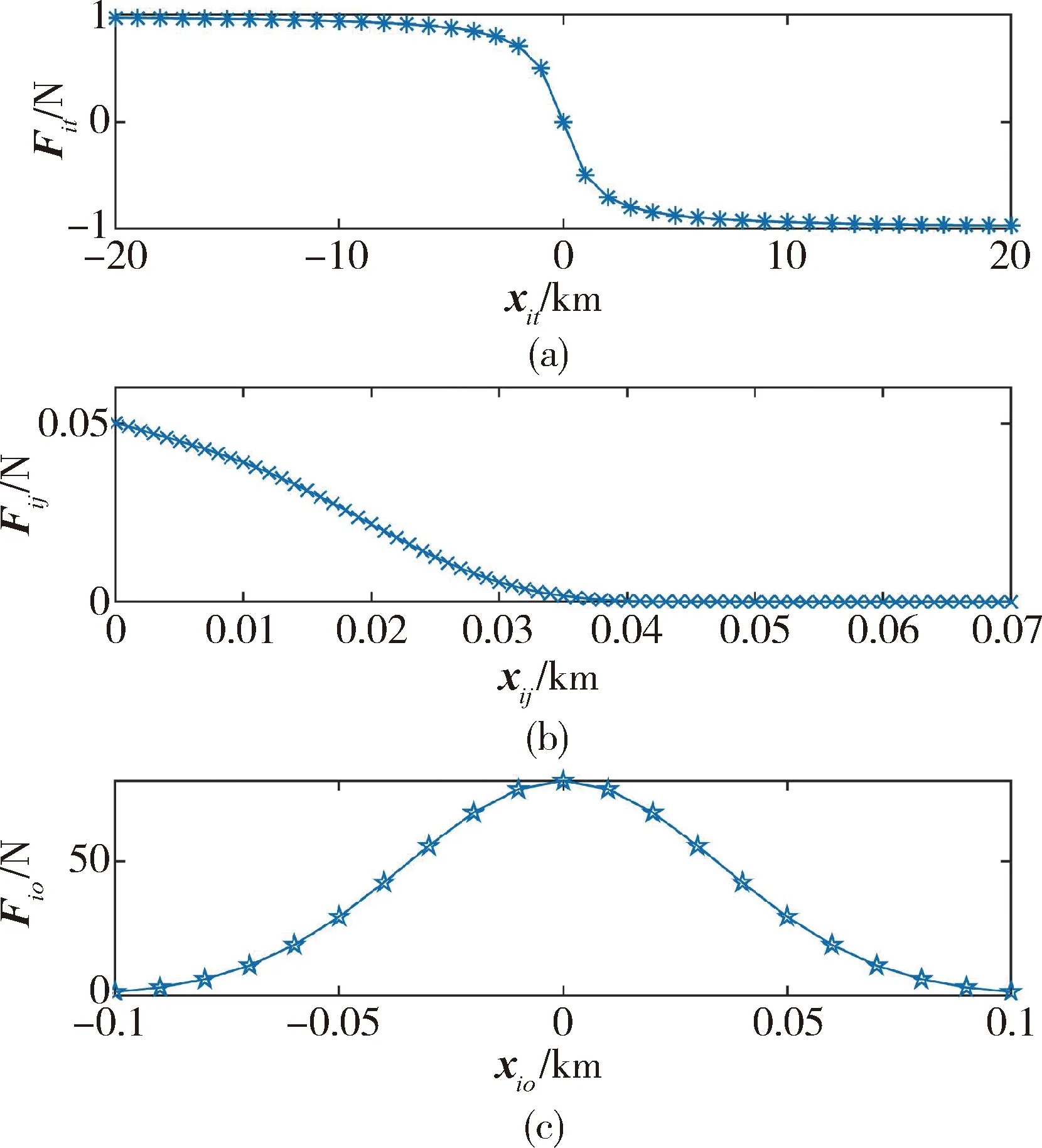
图2 势场作用力曲线图Fig.2 Diagrams of potential field forces

2 星群系统模型

考虑由n颗卫星组成的星群系统，采用二阶群系统模型[16]，星群中第i颗卫星的二阶运动方程可用如下形式表示：

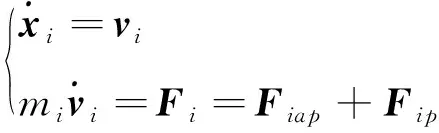
(10)

式中，xi,vi分别为卫星i在惯性系下的位置、速度矢量，Fi为卫星i当前时刻所受合力，其中Fiap为系统整体势场作用力，Fip为空间环境扰动力.

由于星群是以相对紧凑的集群形式运行，集群内航天器间相对运动可由C-W方程描述.C-W方程是CLOHESSY等[17]提出的一个用来描述两颗卫星近距离相对运动的线性化方程，其在航天器轨道坐标系中表示为

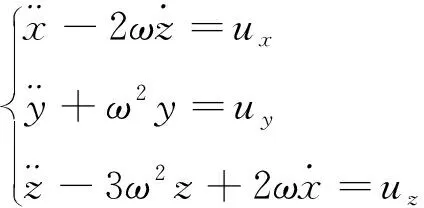
(11)

式中，ω为参考卫星的平均轨道角速度，ux,uy,uz为合外力产生的控制加速度.

航天器轨道坐标系如图3所示，其原点位于航天器质心，z轴由卫星质心指向地心，y轴指向轨道平面的负法向，x轴沿卫星前进方向，与其他两轴构成右手直角坐标系.

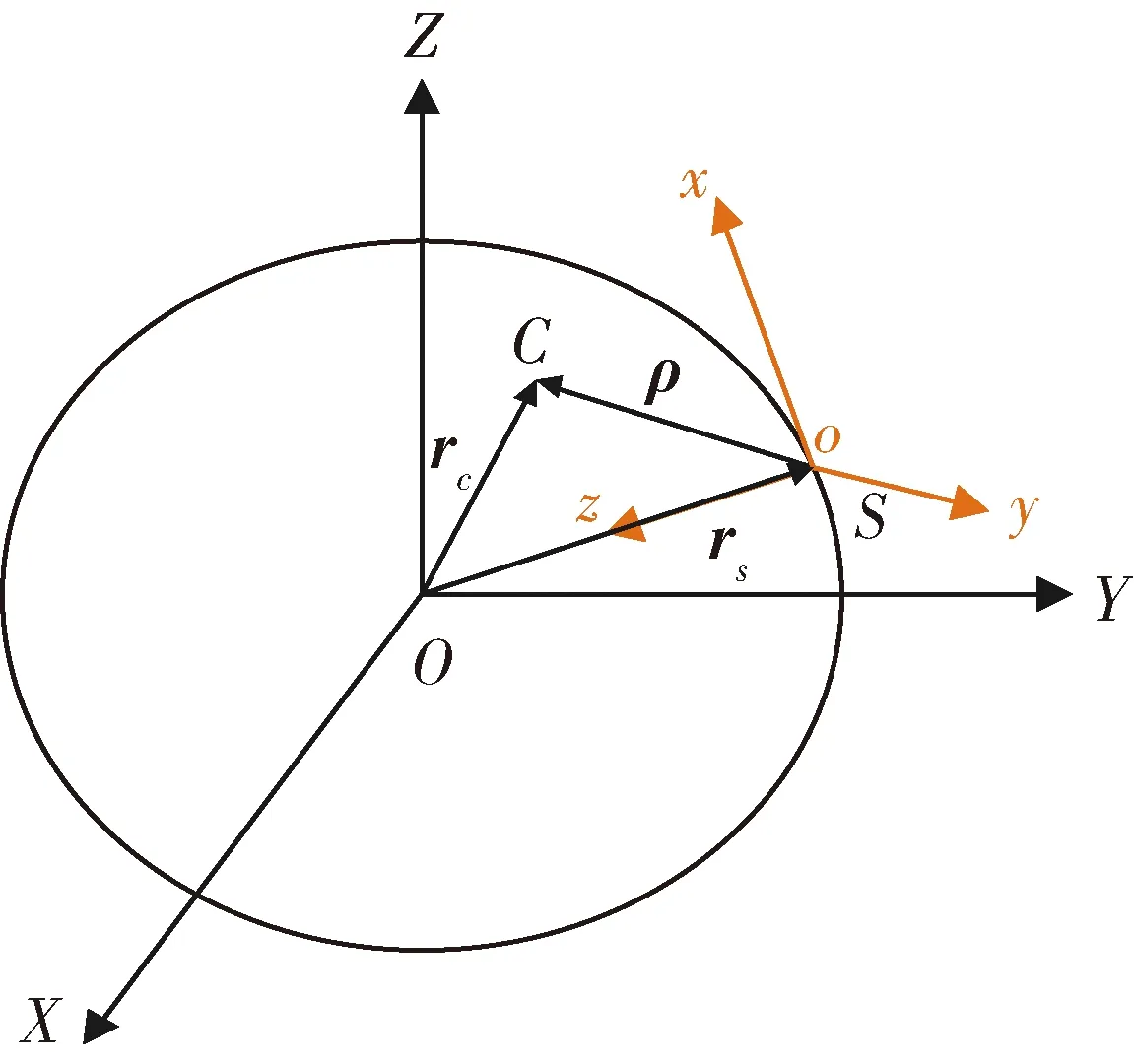
图3 航天器轨道坐标系与地心惯性坐标系的关系Fig.3 The relationship between the orbit coordinate system and the geocentric inertial coordinate system

3 星群松散编队控制

星群松散编队场景如图4所示，多颗卫星由大型航天器携带入轨释放后，可能会存在较大的初始相对状态.为了完成空间任务，需要进行星群松散编队控制，将多颗卫星聚集在一定空域内，同时避免星间碰撞；当遇到空间障碍物时，集群能够及时躲避.

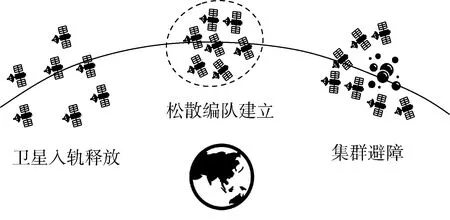
图4 星群松散编队场景示意图Fig.4 Loose formation of satellite clusters

基于第1节中建立的目标吸引势场、星间避碰排斥势场以及空间避障排斥势场，可以有效实现星群松散编队控制.卫星i所受系统整体势场作用力Fiap为

Fiap=Fit+Fij+Fio

(12)

人工势场法控制简单、计算方便，但具体应用时，卫星可能在编队形成前陷入局部最小值点，在该点卫星所受分力相互抵消，从而停滞不前，致使星群编队失败.为了避免人工势场法的局部最小值问题，同时在一定程度上减小控制超调，本文在控制律中引入速度反馈项，此时卫星i所受合力Fi为

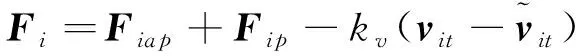
(13)

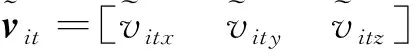
考虑到对卫星进行轨道面外控制需要消耗大量燃料，且两航天器间相对运动在轨道平面内、外是解耦的，因此本文结合C-W方程构建轨道面内速度反馈项.分析C-W方程解析解[18]可知，在轨道面内，为避免相对运动发散，需要控制迹向(轨道坐标系x轴)相对运动中的长期项等于零，即满足

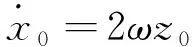
(14)

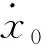
在上述条件下，相对运动轨迹在轨道平面内为一封闭椭圆，若再满足式(15)，则该椭圆的中心位于参考卫星质心.

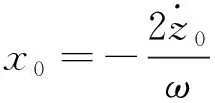
(15)

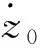
由于轨道面外的简谐运动不会发散，不影响星群整体有界，只要保持轨道平面内航天器间相对距离可控，那么在空间范围内星群一定有界.因此可选取轨道面内的期望相对速度为

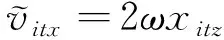
(16)

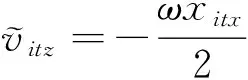
(17)

式中,xit=[xitxxityxitz]是卫星i与目标间相对位置矢量.

4 仿真分析

4.1 松散编队控制仿真

设定星群由50颗100 kg级小卫星组成，初始时刻各颗卫星随机分布在距离目标空域4 km范围内，通过松散编队控制使星群聚集在半径100 m的球域内，且星群中心位于600 km高度近圆轨道上，轨道倾角98°.设卫星尺寸为1 m×1 m×1 m，星间避碰势场作用范围是50 m.设置仿真控制参数如下：

kt=1，kj=1，kv=300，r0=50 m.

选取星群中心轨道坐标系为相对运动坐标系，图5为在相对运动坐标系下，星群松散编队建立阶段和松散编队维持阶段的相对运动轨迹曲线.在本文设计的控制律作用下，各颗卫星自初始相对位置汇聚至半径为100 m的目标球域内，5 000 s左右完成松散编队建立，随后保持松散编队状态.

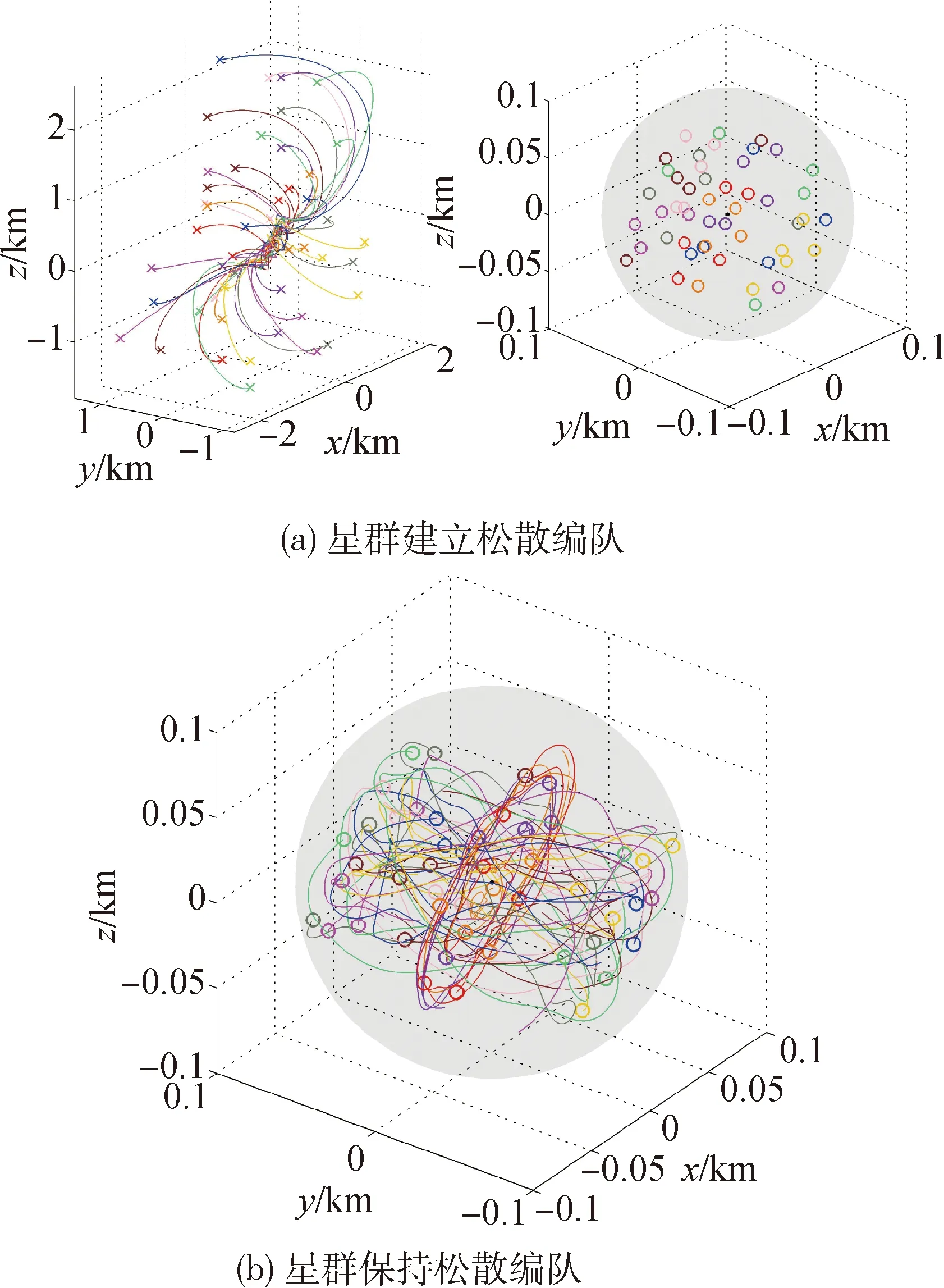
图5 相对运动坐标系下星群的运动轨迹图Fig.5 The trajectories of the satellite cluster in the relative coordinate system

由图6可知，在松散编队状态下，星群中各颗卫星到集群中心的距离一直保持在100 m范围内.同时在星间避碰势场作用下未发生星间碰撞，符合集群松散有界要求.

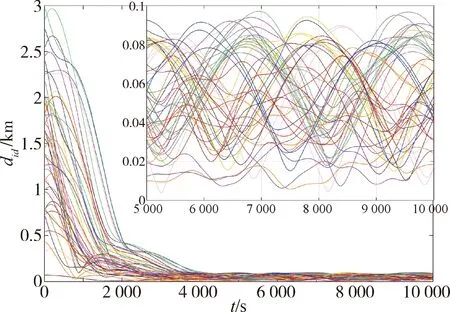
图6 各颗卫星和虚拟集群中心之间的距离Fig.6 The distances between each satellite and the virtual center of the cluster

由图7可知，在前1 000 s星群初始建立松散编队阶段，由于初始相对状态差距较大，各星消耗速度增量较多，但各星所需速度增量约束在10-2m/s以内；在后续松散编队保持阶段，各星所需速度增量为10-4m/s量级.同时为了尽可能减少燃料消耗，在仿真过程中计算各星轨道平面外相对运动的谐振振幅，当轨道平面外谐振振幅小于80 m时，不对法向施加控制作用，因此在松散编队维持阶段，法向速度增量基本为0.

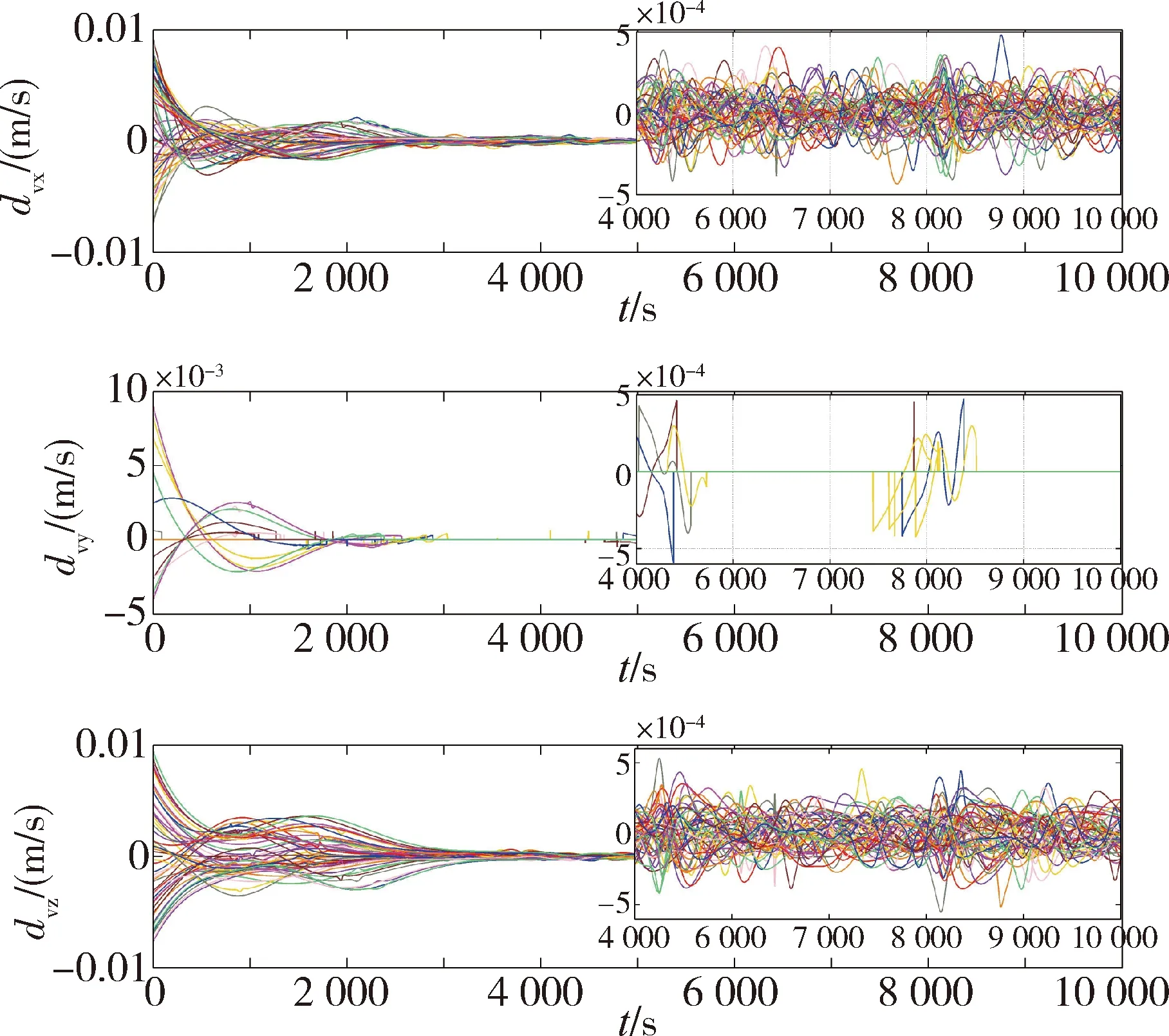
图7 松散编队控制过程中各星的三轴速度增量Fig.7 The three-axis velocity increments of each satellite during loose formation control

4.2 集群避障仿真

由50颗100 kg级小卫星组成的星群运行于半径100 m的球型空域，集群中心位于600 km高度的近圆轨道上，轨道倾角98°.初始时刻，星群接收到指令，追踪同轨道上的另一航天器，同时在目标航天器迹向-300 m处设置一个半径50 m的球型障碍物.对50颗卫星进行集群避障仿真，设卫星的尺寸为1 m×1 m×1 m，星间避障势场作用范围是15 m.选取仿真控制参数如下：

kt=10，kj=1，kv=2 000，ko=0.5，r0=50 m，σ=50 m.

由图8可知，在本文所设计的控制律作用下，集群中各颗卫星可以自发地避开障碍物，到达安全区域后恢复松散编队状态，继续向目标航天器趋近.

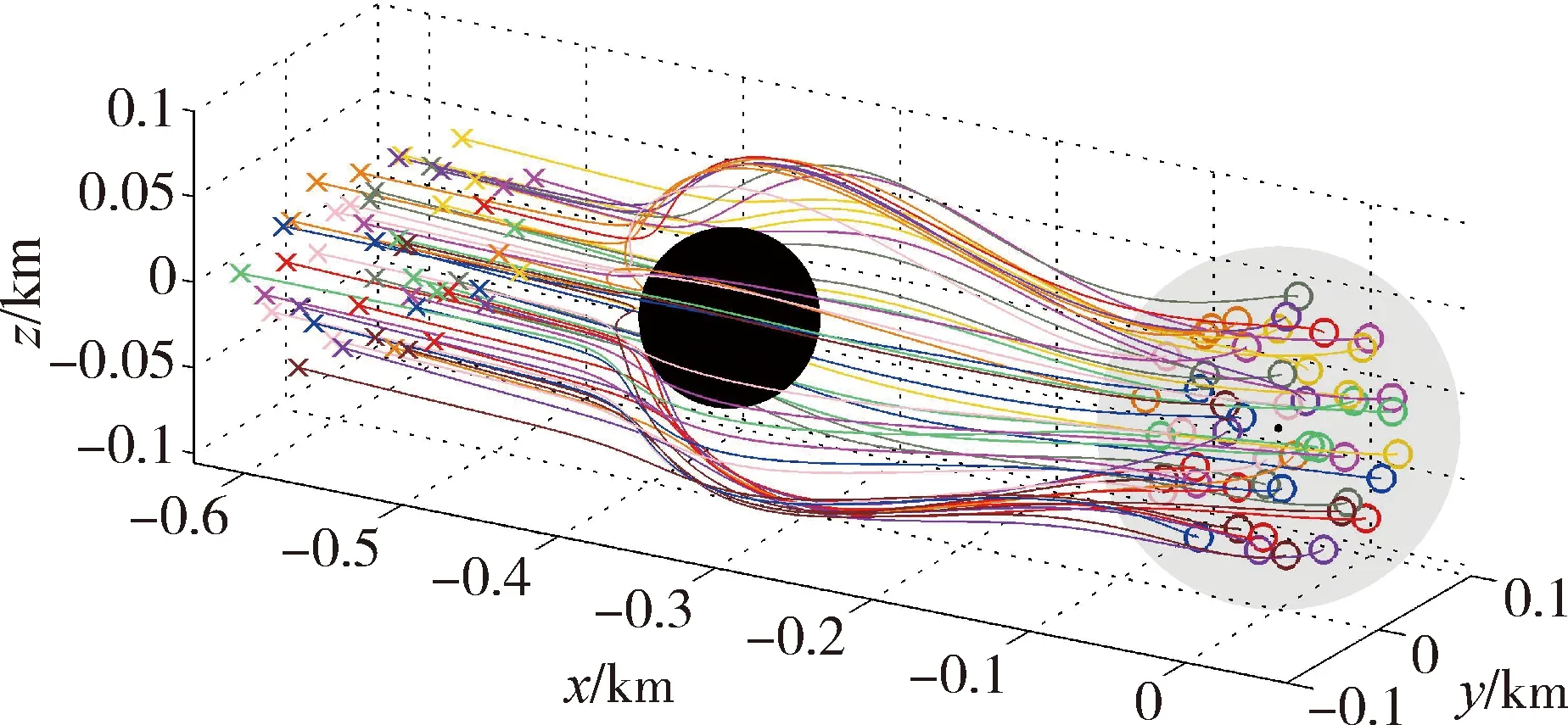
图8 星群避障轨迹图Fig.8 The obstacle avoidance trajectories of the satellite cluster

仿真中预设的障碍物半径为50 m，由图9可知各颗卫星与障碍物边缘之间的距离都大于0，表明集群没有碰触到障碍物，成功实现避障.

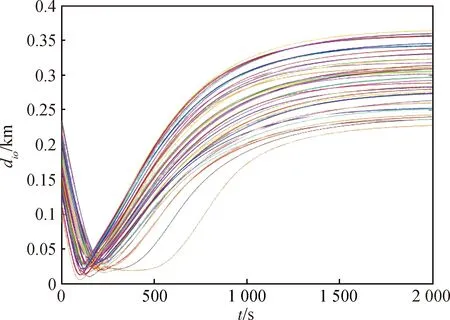
图9 各颗卫星和障碍物边缘之间的距离Fig.9 The distances between each satellite and the edge of the obstacle

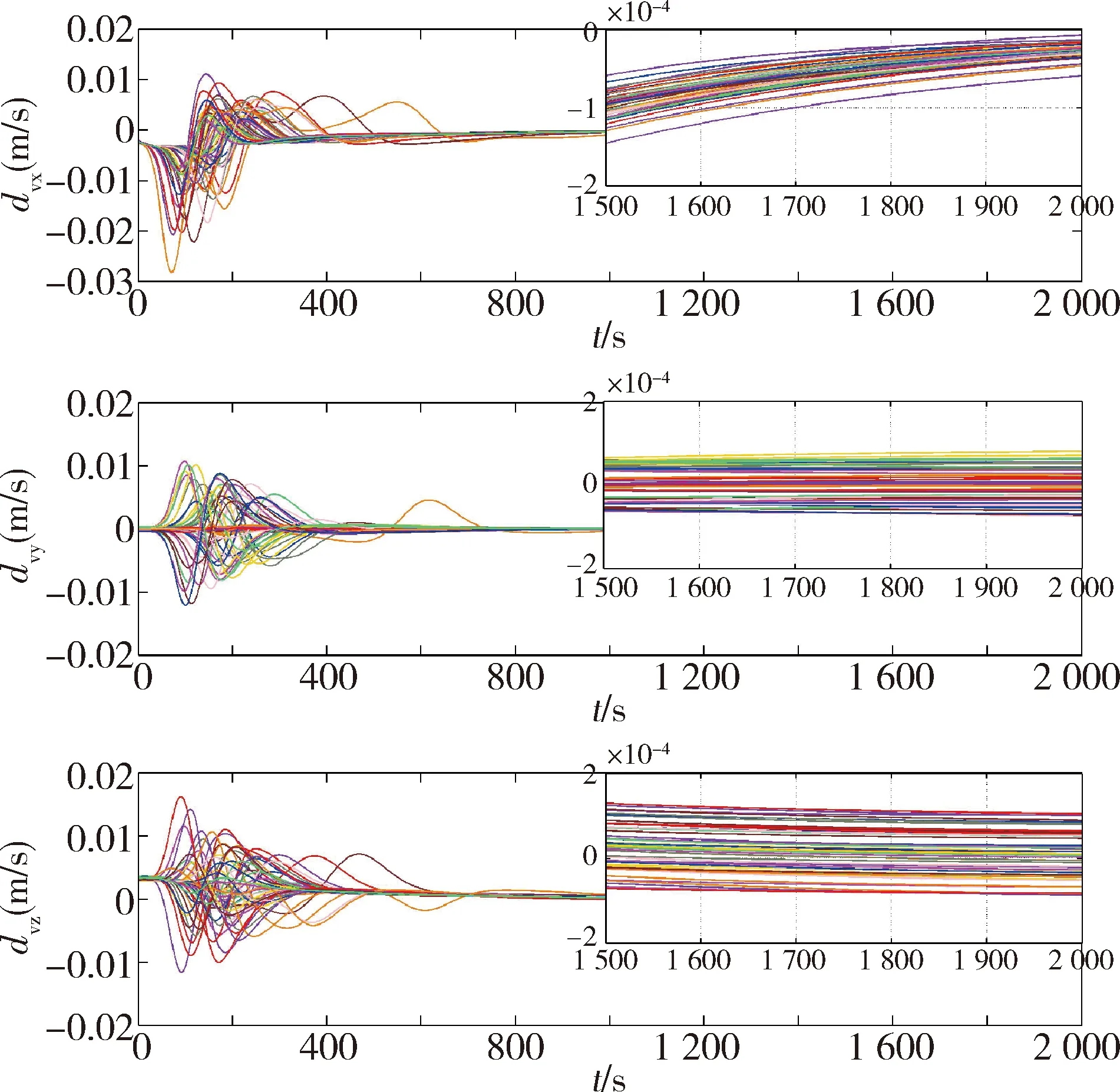
图10 集群避障控制过程中各星的三轴速度增量Fig.10 The three-axis velocity increments of each satellite during obstacle avoidance control

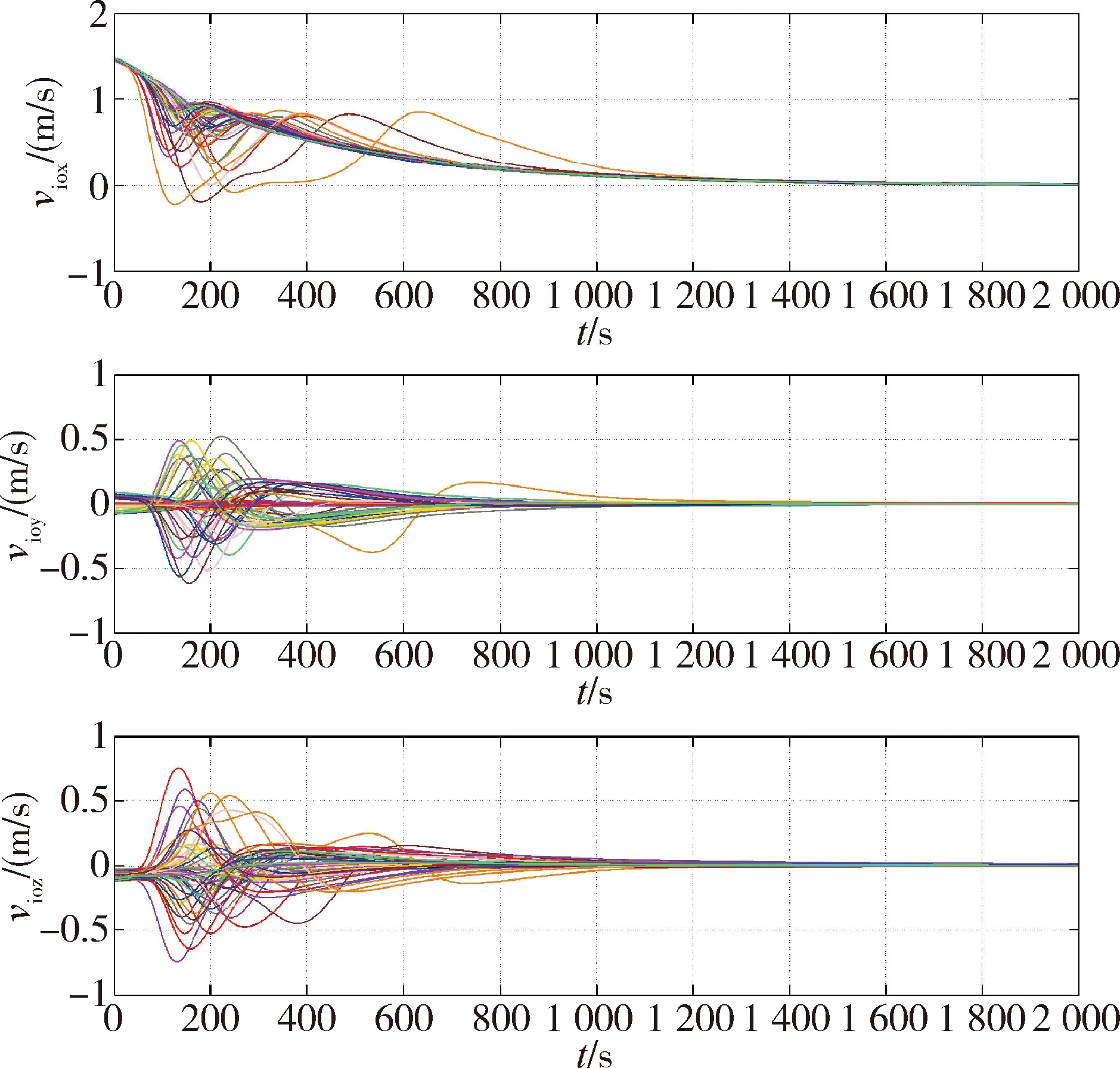
图11 集群避障控制过程中各星与障碍物间相对速度Fig.11 The three-axis relative velocities between satellites and obstacle during obstacle avoidance control

在实际应用场景中，空间环境较为复杂，当星群附近存在动态障碍物时，基于相对位置信息建立的静态避障势场作用效果不明显，尤其是当障碍物相对卫星的速度过大时，或障碍物迎面而来、侧面拦击时，卫星容易躲避不及.为了提高动态避障效率，可以将卫星与障碍物间相对速度或加速度信息引入避障势场中，将静态势场改造为动态势场，增强卫星的预警能力.同时考虑利用相对速度和相对位置的夹角信息，以此判断障碍物是即将远离或是趋近卫星，当动态障碍物朝着远离卫星的方向运动时，无需考虑此障碍物影响，从而避免不必要的燃料消耗.

5 结 论

对于大规模微纳星群，本文结合人工势场法构建集群系统模型，较好地反映了集群内部各颗卫星间相互关系，以及外部环境对集群整体的影响作用.通过在卫星个体控制中引入势场函数，可以有效控制集群整体达到期望运动状态.同时为了减小系统超调，以及避免局部最小值问题，本文结合卫星轨道动力学特点引入了基于相对运动动力学方程的速度反馈控制，可以有效建立并保持星群松散编队，同时实现星间避碰和集群空间避障.文中仿真算例说明了该方法的有效性.