TPEE高分子元件缓冲器粘弹性本构关系求解

魏延刚，王泽岳，宋亚昕

(1.大连交通大学 机械工程学院，辽宁 大连 116028；2.北京多邦汇科轨道车辆装备技术有限公司，北京 101100) *

缓冲器的主要功能是缓和与衰减车体之间的冲击和振动，从而提高列车运行的平稳性和舒适度[1].能量吸收率是缓冲器的一个重要指标[2].TPEE弹性体软硬部分的比例可变，当其处于低应变时有很少的滞后性，是缓冲吸能的良好材料[3].TPEE弹性体缓冲器的能量吸收率与TPEE材料的粘弹性所引起的迟滞损耗密切相关.

相比于弹性材料而言，TPEE的力学性能极其复杂，不同的粘弹性材料在力学性能上也千差万别，然而求得准确的材料本构关系是建立准确缓冲器模型的基础，所以对TPEE本构关系的求解既是重点也是难点.TPEE的研究始于1950年左右，当时ICI公司和Dupont公司在进行对苯二甲酸乙二醇酯聚合时，加入部分聚乙二醇醚得到的共聚物具有一定亲水性，提高了产品的染色效果.10年后，Shivers J C研究表明：这种共聚物具有一定的可逆弹性，通过改变聚醚-非结晶区和聚酯—结晶区的相对浓度，就能将其从硬塑料变成典型的弹性体[4].后来在1972年由美国Dupont公司和日本东洋纺织公司率先将TPEE研制开发成功并商品化，商品名分别为Hytrel和Pelprene.随后，Hochest- Celanese、GE、Eastman、AKZO等10余家公司也相继开发生产出各种牌号的TPEE产品[5].

2007年，国内罗道友等对TPEE的主要性能、特点及应用情况进行了综述[6].2013年，王志文等对TPEE的国内外发展现状进行了阐述，并结合TPEE的结构和性能，总结了TPEE在轨道交通领域中的应用[7].2016年，魏延刚等对用于重载货车缓冲器中的TPEE材料的弹性性能进行了压缩实验，对国产和进口的TPEE材料压缩实验性能进行了对比[8]；2017～2018年，魏延刚等研究了基于TPEE材料的弹性性能对三种TPEE弹性体和金属楔形机构组合式缓冲器进行了研究[9-12].综上所述，国内外对TPEE的研究重心均集中于TPEE的宏观物理性能及其产品的商品化，而对其本构关系，尤其是TPEE的粘弹性本构关系的研究尚未见报导.基于以上背景，本文通过理论与实验相结合的方法，通过基于高聚物粘弹性理论的有限元仿真和真实样机实验相结合的方法，对高分子材料TPEE的本构模型进行试算求解，为新型缓冲器的研发提供有价值的参考.

1 TPEE材料粘弹性本构关系

根据高聚物力学可知，粘弹性材料具有固体性质的同时又表现出某些流体的特征[13-16].虎克定律描述了线性弹性固体的行为，粘性液体的牛顿定律描述了线性粘性液体的行为，而对于线性粘弹性的固体来说，其简单的本构方程就是这两个定律串并联组合起来得到的[15].常见的如Maxwell流体模型、广义Maxwell模型、Kelvin固体模型、广义Kelvin模型、标准线性固体模型等等[16].粘弹性材料特性的影响因素众多，国内外至今仍未出现一套完整的粘弹性本构理论来准确描述材料的粘弹性行为.因而，广大学者试图通过实验方法来进行归纳总结，从而建立相应材料的粘弹性本构模型.

准静态条件下，粘弹性材料的应力和应变会随时间发生变化，即发生蠕变和应力松弛.相关研究表明聚合物的上述特征与材料分子链的重新排布有关：当试件被施加常值载荷时，聚合物中的部分分子链发生错位，这种现象称之为蠕变.当保持固定应变时，聚合物分子链发生伸展来适应变形，从而发生松弛现象[17].在粘弹性材料中，部分外力所做的功将转化为热量而损耗掉，因而该部分能量是不可恢复的，这部分能量称之为耗散能[13-14].

TPEE是典型的粘弹性材料，其力学行为不仅与时间、温度有关，还与载荷的加载方式密切相关.高分子材料TPEE粘弹性本构关系相当复杂.本文拟将粘弹性理论与有限元方法相结合，利用有限元工程软件的材料库中多种材料的数学模型[17]，通过建立多种粘弹性材料的数学模型来仿真TPEE缓冲器的静压实验，并通过与真实的TPEE缓冲器的静压实验结果进行对比分析，从而不断趋近于真实的TPEE粘弹性行为，最终求得比较真实的TPEE粘弹性本构关系.

通过数次的建模试算，本文采用Bergstrom-Boyce滞后模型来描述TPEE的粘弹性特性，Bergstrom-Boyce 滞 后 模型从本质上来说是一种

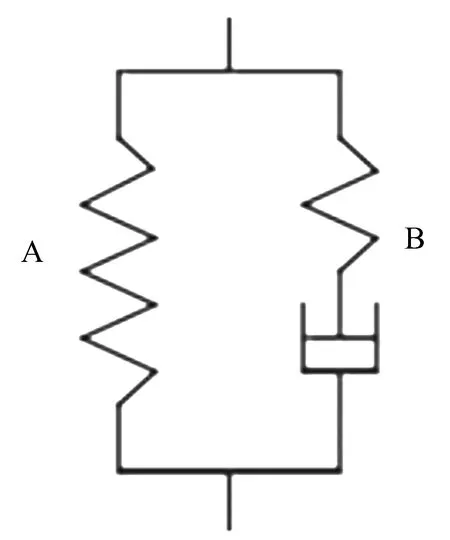
图1 Bergstrom-Boyce滞后模型

经验模型，在该模型中，弹性体的非线性应变率依赖性通过将机械响应分解为与时间无关的纯弹性应力部分A和与时间历史相关的应力部分B两个部分来建模，其中A部分为对应于在长时间应力松弛试验中接近平衡状态的模型响应；B部分则为从平衡状态中捕获的非线性速率依赖偏差，而且假设总应力是A、B两个部分的应力之和.其模型如图1所示.

A部分用弹性本构模型，即弹簧进行描述，B部分则由一个弹性模型和一个粘性模型，即一个弹簧和一个粘壶串联组成，以表征材料应变随时间的变化.B部分的应变率本构方程为[17]：

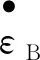
所采用的有限元软件求解器提供了通用的分析能力，它能够求解广泛领域的线性和非线性问题，而且该求解器模块中的Hysteresis滞后模型就是Bergstrom—Boyce滞后模型，另外，若想在软件中应用该模型，还需要一个参数S，也就是模型的等效弹性伸长率，它定义了B部分与A部分的应力比.

通常情况下，S、a、m、c这四个参数对Bergstrom-Boyce滞后模型的影响程度不同，m、c仅与聚合物的分子类型有关，而与填充物无关，其数值不随填充物的不同而改变.而S、a两个参数对模型的影响比较大，S表示模型中B部分的应力(即非弹性力)与A部分的应力(即弹性力)的比值，S越大，耗散就越大，B部分应力对模型的影响就会增大.此外，a增大则意味着应变率在增大，如果通过计算所得到的a比较大，就表明应变率也较大以至于材料来不及蠕变而使滞后减小.

该模型需要与弹性模型一起使用，但另一方面具体参数的辨识又相当复杂.本文通过改变滞后模型参数建立多个不同的缓冲器仿真模型，参数的调整在相应的物理区间内进行，比如：蠕变参数a保持了有效蠕变应变率表达式量纲的一致性，一般为一个非负值；表征有效应力对应变率的相关系数m的值通常大于1；表征蠕变应变对应变率的相关系数C的取值区间为(-1,0).最后通过对比分析样机试验与多个不同缓冲器仿真模型的载荷—行程曲线，来实现对TPEE材料的超弹性和粘弹性本构关系的求解.

2 缓冲器的结构原理与静压试验

2.1 缓冲器的结构原理

本文研究的缓冲器装配关系示意图如图2所示.高分子TPEE弹性体是缓冲器的吸能元件，弹性体之间由金属隔片隔开，不仅能够保证缓冲器在工作过程中轴向受力均匀，而且，弹性体和金属隔片之间的摩擦也可提高缓冲器的吸收效率.

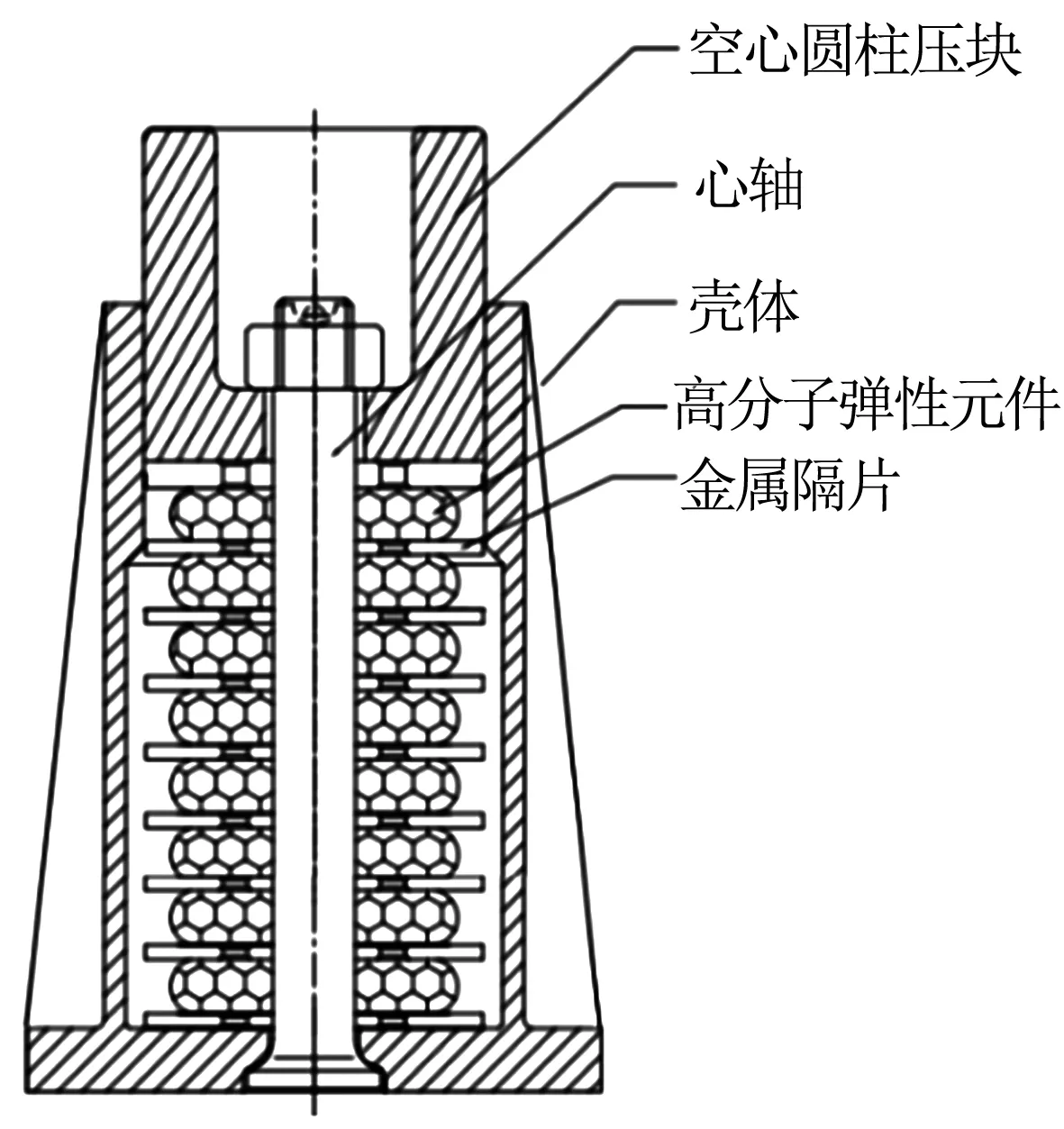
图2 TPEE弹性体缓冲器装配示意图

当冲击载荷沿轴向作用于空心压块上时，压块推动金属隔片和TPEE弹性体，使轴向载荷通过金属隔片作用在壳体的底部.在此过程中，轴向力使TPEE弹性体发生轴向压缩变形而吸收冲击能量，同时金属隔片与TPEE弹性体之间的径向摩擦也将消耗一部分冲击能量.当冲击载荷消失后，弹性元件恢复变形而推动空心压块由下向上运动，最终所有元件恢复到受冲击载荷前的状态.

2.2 缓冲器样机静压试验

本文用BDHRV-300T-1M-125MM静压实验机对所研究的缓冲器进行了压缩实验，并用本课题组所研发的缓冲器静压试验数据采集系统记录静压试验过程中的载荷与位移数据，并将数据绘制成曲线.测量系统力传感器的量程为3 000 kN，精度G5，位移传感器量程为125 mm，线性度为0.1%.课题组对6台物理样机分别进行了静压试验.

试验中，缓冲器的高分子弹性体材料为国产的热塑性聚酯弹性体(TPEE)，弹性体数量为8个，隔片数量为9片(厚度6 mm/片).6台物理样机的静压试验实验结果相近，在此取其中一台样机的试验结果进行分析，静压曲线如图3所示.该缓冲器样机的行程为89.41 mm，最大阻抗力为2637.76 kN.

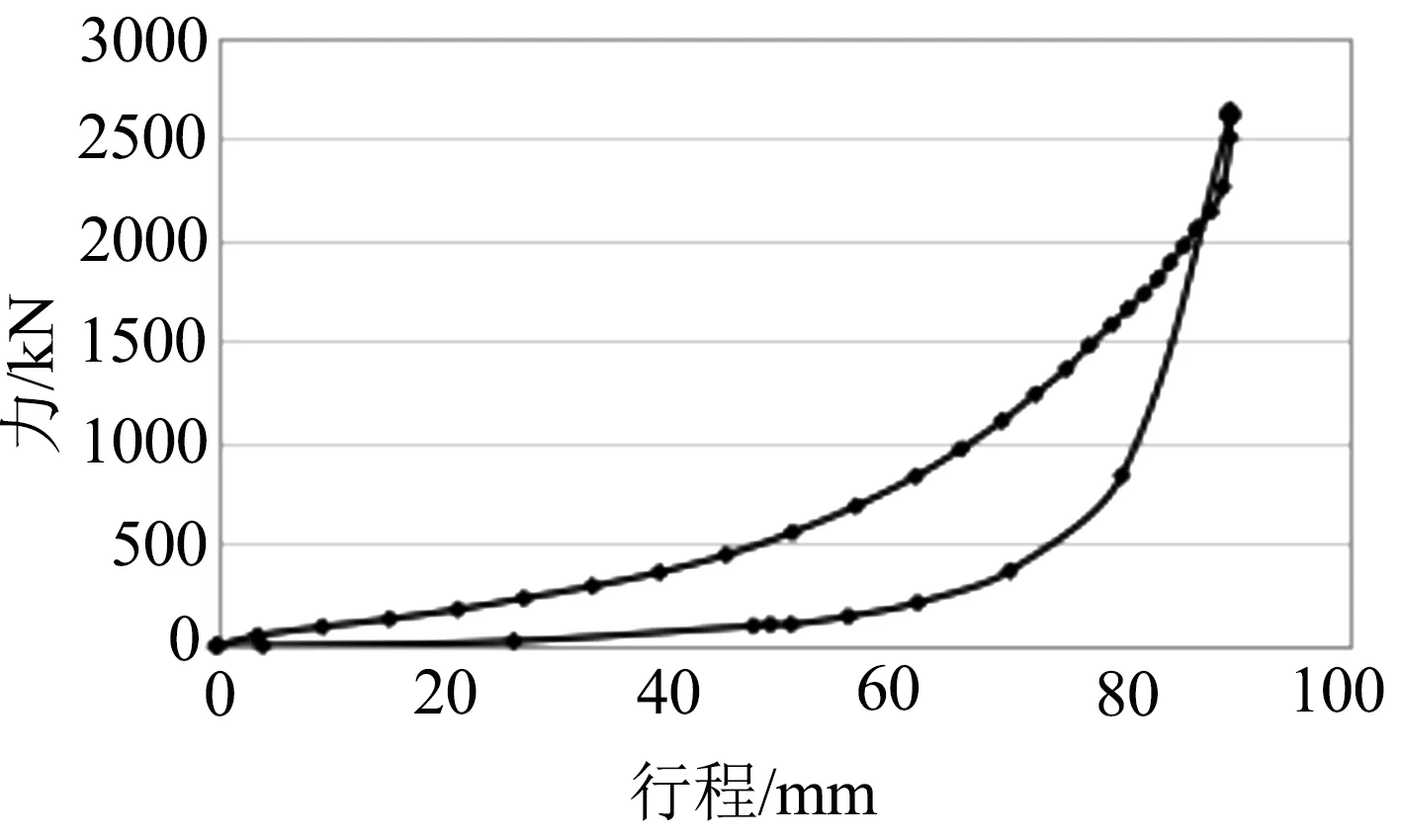
图3 缓冲器样机静压试验曲线

为定量分析该缓冲器样机的容量和吸收率，本文对试验得到数据用MATLAB进行曲线拟合，然后通过积分来计算缓冲器在压缩和回弹时的能量，从而确定该缓冲器的缓冲特性.

首先将缓冲器压缩过程的力和行程数据输入到MATLAB主窗口中，再打开MATLAB拟合工具箱，将X轴的标签设为Displacement，Y轴的标签设为Force，经多次拟合尝试后，选择4次多项式对压缩过程的数据进行拟合，拟合得到的4次多项式如下：

同样方法得到的缓冲器回弹的6次拟合多项式如下：

由MATLAB拟合工具箱得到的拟合曲线和原数据的吻合程度达到了95%以上，因此，可用得到的拟合曲线近似代替样机试验的缓冲器特性曲线，可通过对拟合曲线的方程进行积分从而近似得到该缓冲器样机的容量和能量吸收率，通过计算得到的结果如表1所示.

表1 高分子弹性体缓冲器的容量和吸收率

从表中可以看出，该高分子弹性体缓冲器的容量约为60 kJ，达到了我国铁道行业标准TB/T 1961-2016中对普通货车缓冲器的容量要求(≥50 kJ)；吸收率约为57%，与行业标准中对吸收率的要求(≥80%)尚有差距，有待提高.

3 缓冲器的有限元静压试验仿真及TPEE本构关系求解

3.1 有限元建模

为减少计算量，提高计算效率，在对缓冲器样机静压试验进行有限元仿真时，仅对缓冲器关键部件进行了精确建模，TPEE弹性体及隔片组件是缓冲器的核心部件，因此，对TPEE弹性体的准确建模是对整个模型正确分析的基础.TPEE弹性体缓冲元件的实物图如图4(a)，其剖切开后的内部结构图如图4(b).由其实物图可以看出，弹性体的形状为圆环形，内部设有空腔，将其切开后，空腔变大，弹性体会涨开.

(a)实物图 (b)剖切图图4 TPEE弹性体元件实物图

根据TPEE弹性体实物，使用Creo对其进行三维建模.图5为TPEE弹性体的三维模型图和草绘截面图，其中图5(b)中的具体数据为：外径半径L=79 mm，内径至外径之间的距离A=52.5mm，弹性体最厚厚度的一半H=18.18 mm，弹性体内部空腔最大值K=2.36 mm.

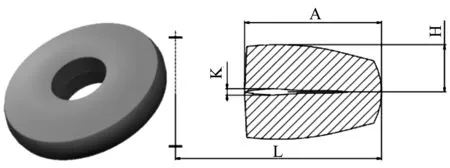
(a)三维模型图 (b)草绘截面图图5 TPEE弹性体三维模型图和草绘截面图

TPEE弹性体和隔片组件依次装配，压块装配在隔片的上方，装配图如图6所示.

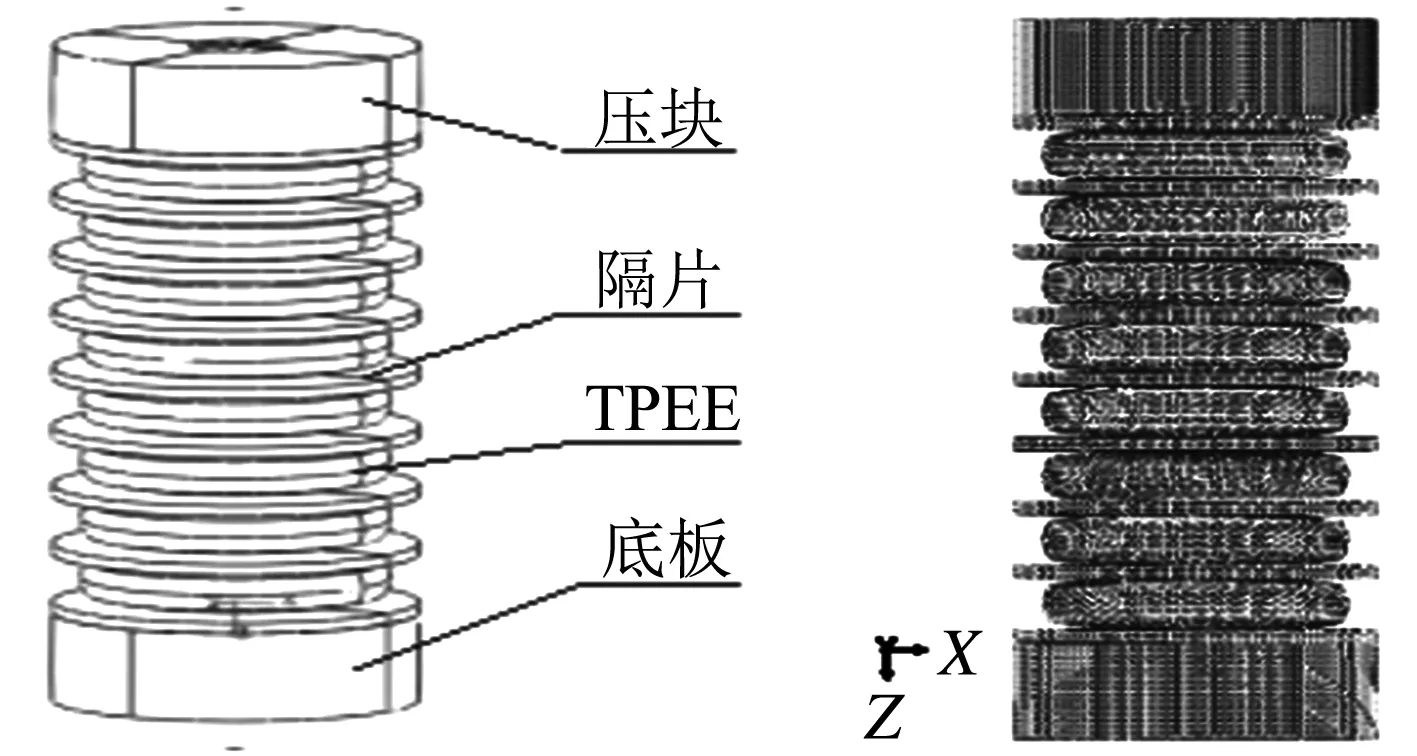
图6 缓冲器仿真装配图 图7有限元模型网格图

在对模型进行网格划分时，为了保证计算精度，将模型中的所有零件网格密度设为一致，有限元模型网格图如图7所示.对于模型中的钢制隔片，设置其弹性模量为210 000 N/mm2，泊松比为0.3；在定义TPEE的材料属性时，其弹性模型由TPEE压缩试验修正后的数据[14]来描述，Bergstrom-Boyce滞后模型参数由单轴压缩实验数据和静压实验的加载速率进行辨识，将材料参数输入到有限元软件中，软件可以对输入的数据进行评估，并给出吻合试验数据的能量模型，以该能量模型为基础进行静压仿真，保证了仿真结果的准确性.接触属性的设置中，钢制隔片与TPEE之间的摩擦系数根据实验确定[15]，取为0.18.仿真模型设置压缩和回弹两个分析步，在正确设置接触和边界条件之后，对压块施加2 637.76 kN的轴向(Z轴方向)的载荷，加载以及卸载的载荷幅值根据样机试验中力传感器所记录的数据制定，以实现对该缓冲器压缩与回弹过程的真实仿真.

3.2 TPEE本构关系求解

经过数次的建模和试算，得到了相应的仿真结果，通过与样机实验结果对比求得了仿真结果与样机实验结果最接近的TPEE本构关系，相对最优的TPEE本构关系的四个参数为：S=0.719、a=5.25、m=5.086、c=-0.041.

在此仅给出相对最优的TPEE本构关系的静压仿真的结果.仿真模型的最大位移为82.24 mm，表2中列举了部分数据，由全部数据画出的位移与载荷曲线如图8所示.

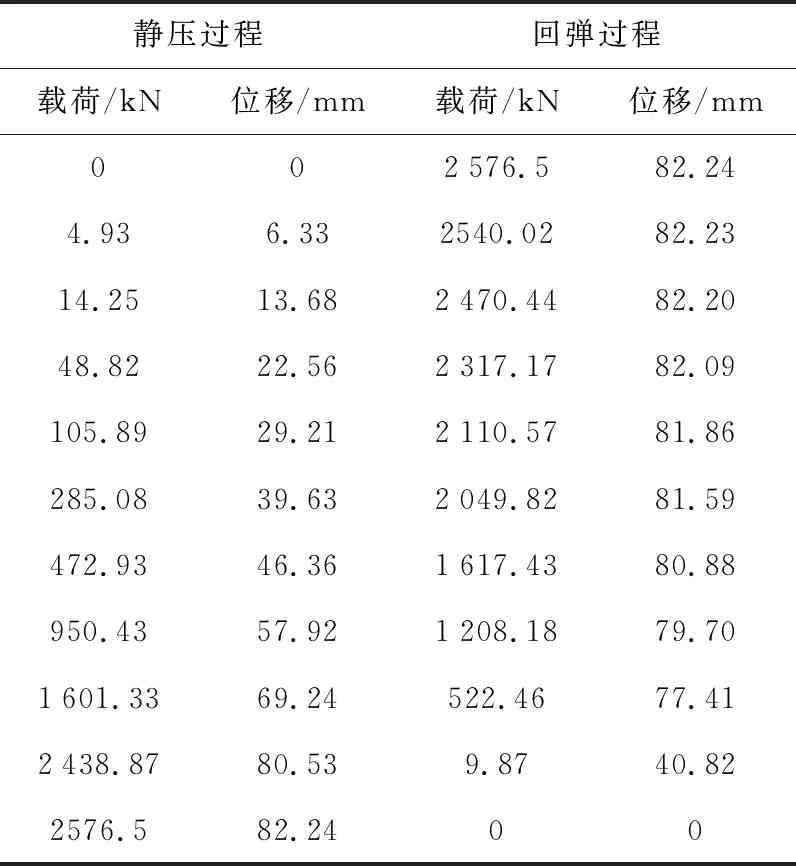
表2 缓冲器静压仿真中的载荷与位移

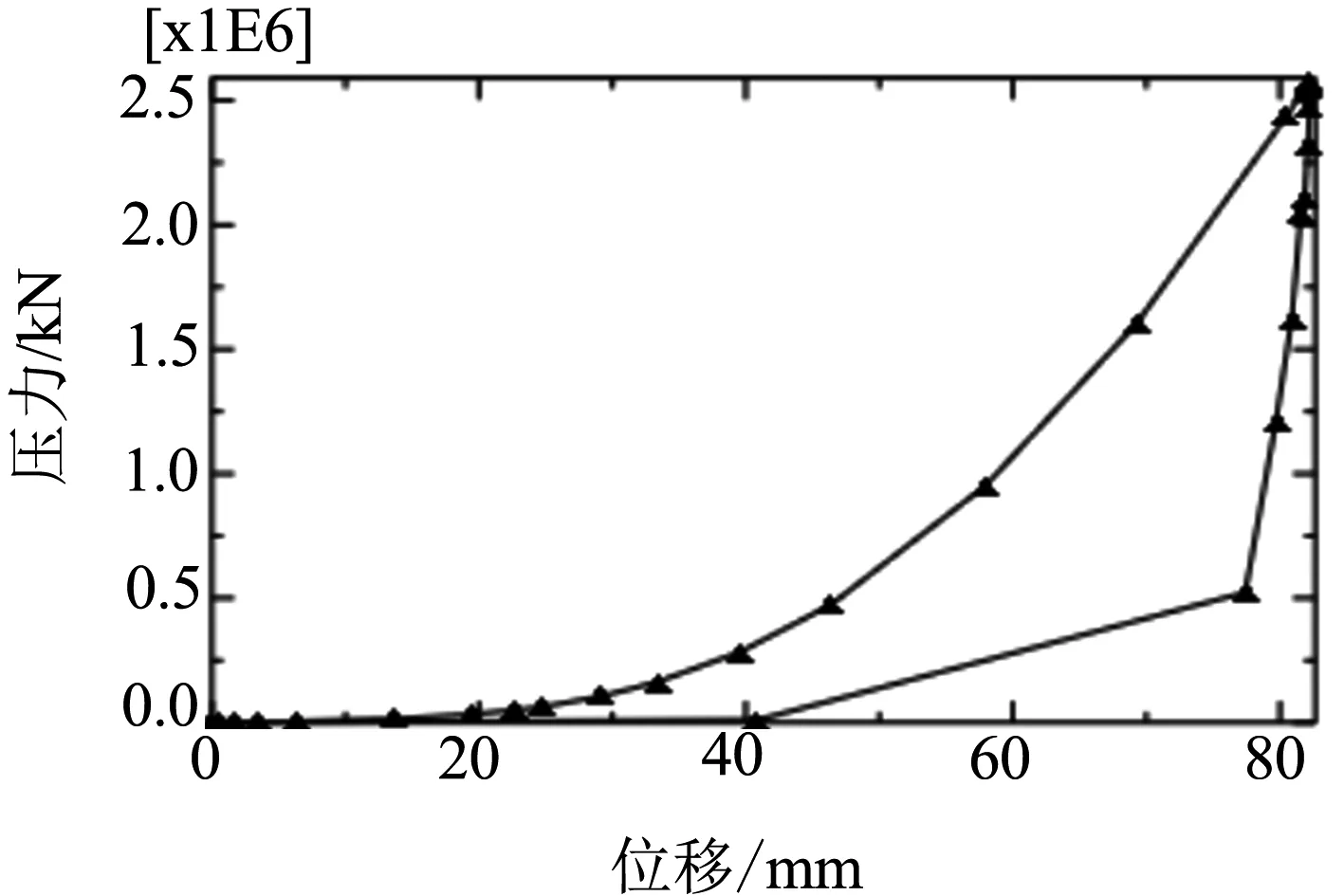
图8 相对最优的TPEE本构关系的缓冲器静压仿真曲线

通过比较样机试验和静压仿真的载荷-位移曲线，可以看出两个曲线的吻合程度良好，证明了仿真过程的正确性.回弹过程中，TPEE宏观上表现出良好的滞后性，当外力完全撤掉时，还有相当部分的位移，避免了缓冲器回弹过程中的刚性冲击.

下面重点分析该缓冲器在工作过程中的能量损耗.缓冲器的能量消耗主要由两部分组成：一部分是TPEE弹性体在受载后因粘弹性特性而消耗掉的粘弹性耗散能，另一部分是TPEE弹性体变形后与金属隔片相摩擦而消耗掉的摩擦耗散能.

能量输出是有限元软件一个重要部分，可以应用在各种能量分量之间的比较来帮助评估一个分析是否得到了合理的响应.整体模型的能量平衡表述为[16]：

ALLIE+ALLVD+ALLFD+ALLKE=ALLWK

(1)

其中，ALLIE为内能；ALLVD为粘性耗散能；ALLFD为摩擦耗散能；ALLKE为动能；ALLWK为外载荷所做的功.内能ALLIE是能量的总和，包括可恢复的弹性应变能ALLSE、非弹性过程的能量耗散(例如塑性)ALLPD、粘弹性或者蠕变过程的能量耗散ALLCD和伪应变能ALLAE：

ALLIE=ALLSE+ALLPD+ALLCD+ALLAE

(2)

式(1)中的粘性耗散能ALLVD是由阻尼机制引起的能量耗散，包括体粘性阻尼和材料阻尼，作为一个在整体能量平衡中的基本变量，粘性耗散能不是指在粘弹性或非弹性过程中耗散的那部分能量，本文研究的模型中粘性耗散能ALLVD=0.由于本模型为静态分析且模型中不含塑性材料，因此式(1)中的动能ALLKE和式(2)中的非弹性过程的能量耗散(塑性)ALLPD恒为0.伪应变能ALLAE则包括存储在沙漏阻力以及在壳和梁单元的横向剪切中的能量.

取ALLVD=0，ALLKE=0，ALLPD=0，将式(2)代入式(1)，得到本模型总的能量平衡方程：

ALLSE+ALLCD+ALLAE+ALLFD=ALLWK

(3)

由上式可以看出，缓冲器在工作过程中，车体之间的冲击力所做的功，一部分转化为TPEE弹性体的弹性势能ALLSE，这部分能量在缓冲器的回弹过程中依然会作用回车体，对车体造成冲击.外力做功的另一部分则由TPEE弹性体的粘弹性(即粘弹性耗散能ALLCD)和缓冲器内各零件之间的摩擦(摩擦耗散能ALLFD)耗散掉.

在有限元仿真的历史变量输出中，可以分别读取外力做功ALLWK、存储的弹性应变能ALLSE、粘弹性耗散能ALLCD和摩擦耗散能ALLFD.需要注意的是，由于模型中涉及到粘弹性材料，即在模型中输入了Bergstrom-Boyce滞后模型，那么在输出的历史变量中，弹性应变能ALLSE为由第1节中介绍的A、B两部分的应力之和计算得来，而由1.2节中我们知道，A部分本就对应于在长时间应力松弛试验中接近平衡状态的模型响应，而B部分则为从平衡状态中捕获的非线性速率依赖偏差，以此偏差来计算模型中所产生的蠕变，因此对于整个模型来说，弹性应变能ALLSE应为仅由A部分的应变来计算.即A部分的粘弹性耗散能为历史变量输出中总粘弹性耗散能的1/(1+S)，其中S为模型中B部分的应力(即非弹性力)与A部分的应力(即弹性力)的比值.即：

ALLSEA=ALLSE/(1+S)

(4)

表3是压块在下压和回弹过程中分别处于某些位移时刻的各能量分量值，图9是由模型的能量数据画出的能量曲线，由于仿真结果伪应变能ALLAE基本为0，所以图中未画出，而缓冲器内各零件之间的摩擦耗散能ALLFD相对外力做功ALLWK、存储的弹性应变能ALLSE、粘弹性耗散能ALLCD很小.

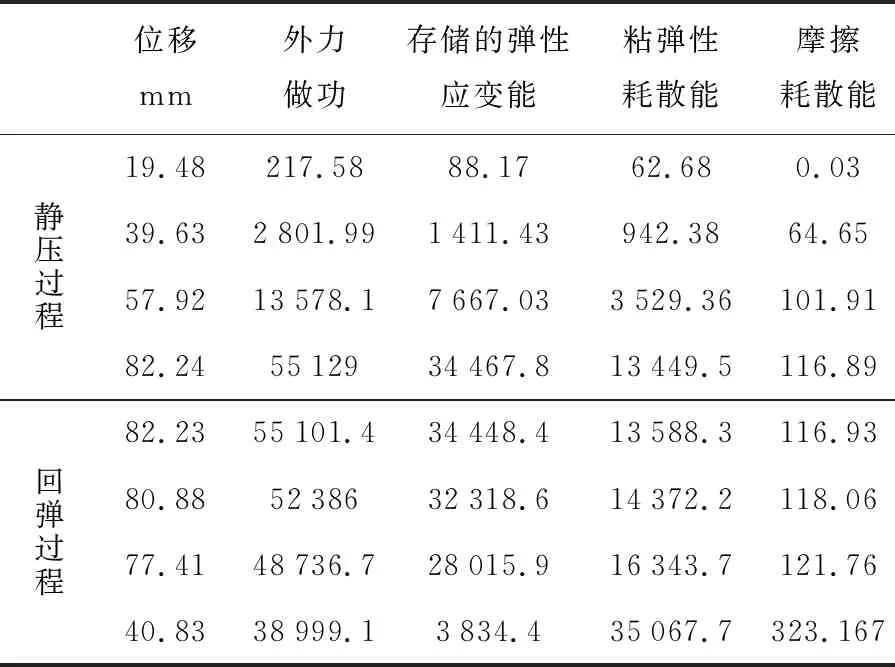
表3 静压试验仿真过程能量数据 J

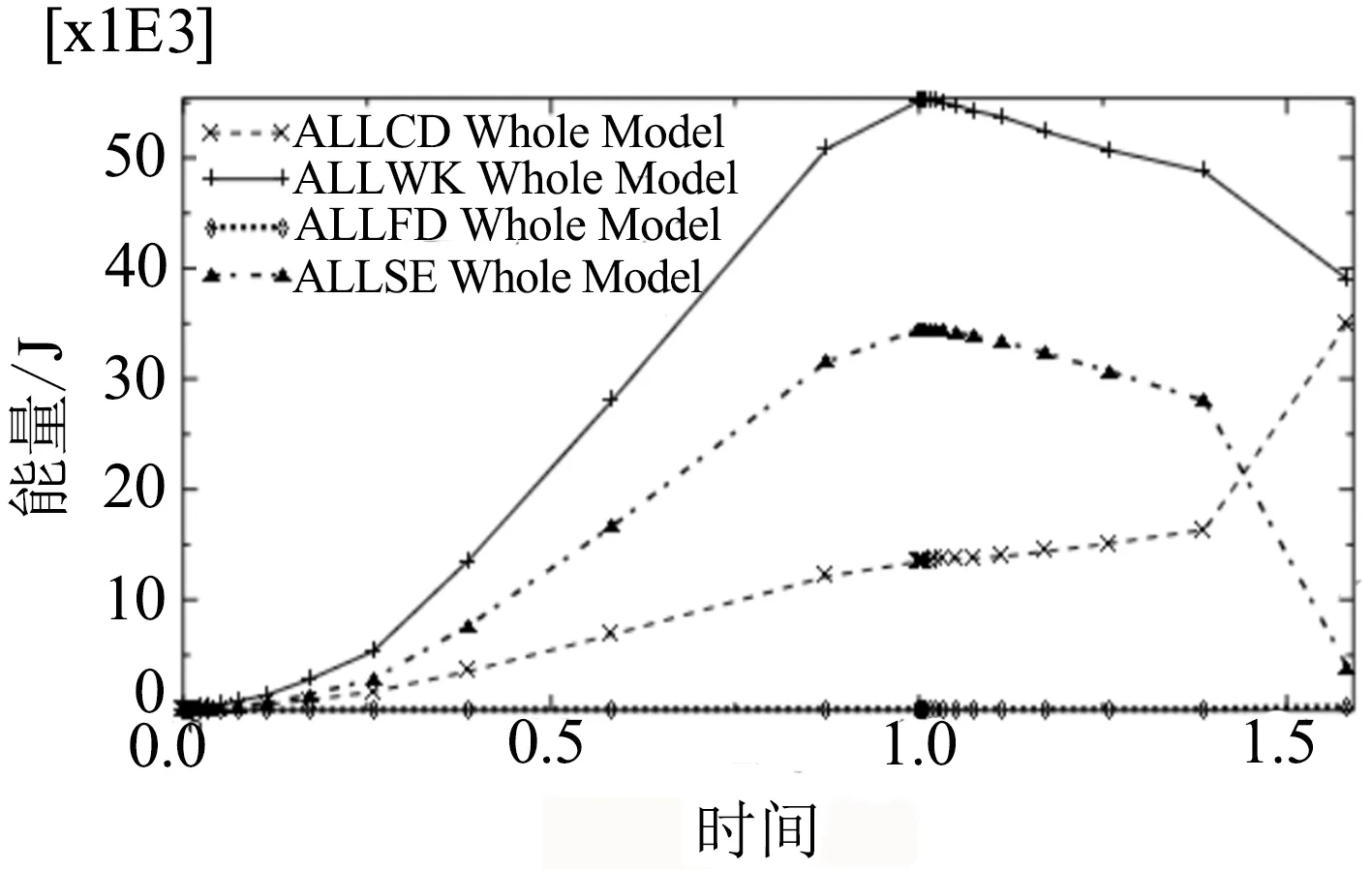
图9 缓冲器静压过程能量曲线

通过能量数据和曲线可以看出：该模型在仿真的过程中能量基本守恒，有限元仿真中缓冲器的容量为55.13 kJ，与样机实验中的容量59.79kJ相差约7.8%.，在缓冲器的全压缩过程中，TPEE弹性体的粘弹性耗散能为35.07 kJ，粘弹性耗散率为63.61%；摩擦耗散能为0.3kJ，摩擦耗散率为0.54%，因此该缓冲器总的能量吸收率为64.15%，该值与缓冲器的样机实验的结果存在些许差距，二者相差约11.19%，究其原因，可能是因为模型的回弹过程输出的数据点不是很均匀从而造成误差.同时我们看到，缓冲器的TPEE弹性体耗散掉了大部分外力的功，从而使货车在行驶过程中避免了车体之间的刚性冲击；缓冲器在工作过程中，TPEE弹性元件与金属隔片之间的相对位移较小，这也是该种缓冲器摩擦耗散能较小的原因.

4 结论

通过有限元仿真试算方法，最终采用Bergstrom-Boyce滞后模型来描述TPEE弹性体的粘弹性特性，并将其应用在车钩缓冲器静压试验的有限元仿真，仿真所得出的力-位移曲线与样机实验所测得的结果吻合程度良好，证明了Bergstrom-Boyce滞后模型可以较恰当的描述所采用的国产TPEE的力学特性.从仿真结果中读取出缓冲器的各能量耗散，TPEE弹性体的粘弹性耗散能占外力做功的的大部分，表明了TPEE良好的缓冲吸振特性，仿真结果可为新型缓冲器的研发提供参考.