面向首都大学生的定制公交线路规划模型及算法研究

梁宇杰,宋瑞,王宇擎,吴兆田

(北京交通大学 交通运输学院，北京 100044) *

市面上定制公交存在很多问题，如覆盖线路缺失，上座率低，难以盈利等[1]，但目前的研究多针对泛用户群体进行站点，线路优化[2]，或者针对运营模式提供改进，如斐明阳等人提出的实时预约制[3]，钟燕妹提出的智能化管理[4]等，鲜有从细化需求的角度，优化定制公交的用户结构，并由此开展具体的模型构建、算法研究和应用改进.笔者认为，用户群多样，分布不规律，需求分散，是目前定制公交存在各种问题的一大根本因素，因而本文提出针对特定用户群体的定制公交线路规划模型及算法研究.选择首都大学生作为特定用户群，一方面是因为大学生多处于郊区，路程遥远，日常出行，节假日往返火车站等交通需求不易得到满足，符合集约化交通的服务条件.另一方面是大学生具有结伴出行，出行可诱导，出行弹性高等特点，具有很强的群体性研究价值.

1 大学生出行行为分析

根据大学生的性别、年级、交通出行方式、对定制公交的看法等，进行了问卷的设计.通过在各大高校线上线下投放及回收，分析数据如图1，得出大学生出行与定制公交的联系：①出行习惯上，定制公交很好地满足了市区和郊区大学生的出行习惯，短途则代替普通公交，长途则相当于定制班车，且价格适中、方便快捷，符合大学生的实际经济情况和出行习惯.②出行心理上，郊区大学生更喜欢将购物和其他目的的出行结合起来形成多目的出行，且多倾向于去城市中心，故日常出行具有一定的游玩休闲性质.开展定制公交旅游专线，不仅可以收集到需求数据，且集约化程度高、聚类效率高、运行周转率高.③出行需求上，无论是市区高校学生还是郊区高校学生，在往返火车站回家或出游时，都普遍反映存在人流拥挤、大宗行李携带不便、换乘麻烦、耗时长、人身财产安全难以保障等问题，如果可以提供直达式交通则有利于缓解这些问题.且通过设置时间窗等算法可实现预约到达时间等功能，使得出行更加高效省时.④交通需求诱导和平台社交功能上，大学生出行具有从众性，喜欢结伴出行，集约化的出行方式可以很好地诱导大学生集体出行.若应用于小程序，可提供社交功能，大学生可通过该线上平台进行交友沟通，这种附加的社会属性更有利于诱导大学生出行，产生更好的出行效果.⑤出行方式选择上，结果显示大学生对直达性的诉求最高，且高于价格因素，可见频繁换乘已经成为影响大学生出行的重要因素，且大学生普遍愿意牺牲一定的价格来保证直达性，这和定制公交的收费模式不谋而合.

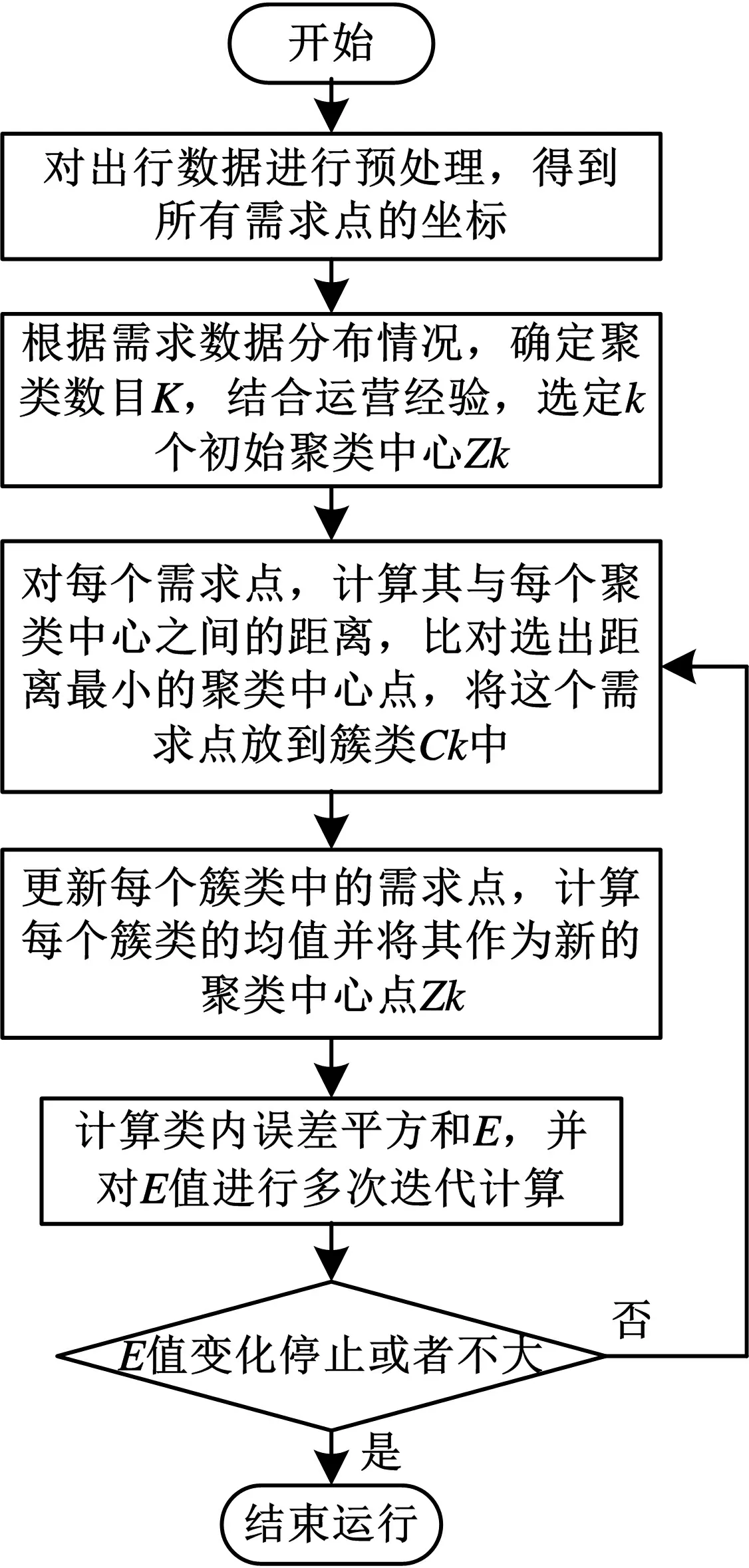
图1 部分问卷调查结果

2 定制公交站点和线路规划

针对上述问题，进行具体的模型构建和算法研究，先将乘客出行时间聚类，将出发或到达时间相近的乘客安排到同一趟路线上，对上车点进行聚类规划.然后找到距离、时间等约束，以总行驶里程最小为目标函数，构建线路规划模型，通过蚁群算法求解，得到最优解.

2.1 聚类方法分析

2.1.1 聚类步骤

常见的聚类算法方法有K-means, K-Modoids, Clara等，其中K-means算法逻辑思路和实现难度都具有简单直接的特点，且算法易于理解，在时间和坐标这类低维数据集上有不错的效果.以K-means聚类算法应用于站点聚类为例，具体步骤如图2，其中类内误差平方和计算公式如式(1)[5]，p为簇类Ck中的需求点.

(1)

2.1.2 聚类孤立点的剔除

在聚类过程中，有一些用户的需求时间点不同大众，如果满足这一小部分人的需求使得整条线路的时间成本很高，这些称为孤立点，对于这些需求，我们会提前告知乘客其时间不合适，并通过计算给出几个合适的时间段供其挑选.

下面介绍如何找出这些孤立点.

设有一数据集，通过聚类算法分析后，将分割成k个(k大于实际需要的聚类群体数量)不相交的数据集合V1,V2,…,VK，计算出这k个数据集合的样本个数为|V1|，|V2|，… ,|VK|; 并假设|V1|<|V2|<… <|VK|;设m为它们的样本个数的中位数 ，给定阈值参数ε和整数b，若满足条件：

m/|vb|≥ε

(2)

m/|vb+1|≥ε

(3)

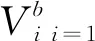
使用上述的K-means方法应用于站点的规划，由此可得上车所在区域的站点分布情况，同时将各个上车点进行编号，为下一步做准备.

图2 K-means聚类算法具体步骤

2.1.3 时间聚类和站点规划

时间聚类属于一维数据的聚类，而站点规划属于二维数据的聚类.先进行时间聚类，将出发或到达时间相近的乘客安排到同一趟路线上.在时间聚类的基础上，对于同一个时间区间的上车点应用上述K-means方法用于站点的规划，由此可得上车所在区域的站点情况，同时将各个上车点进行编号，为下一步做准备.

2.2 线路规划模型建立

该问题可以归结为车辆路径问题(Vehicle Routing Problem, VRP)[7]，已知乘客的需求、上下车点、期望到达时间，假设定制公交全程都以平均速度来运行，各站点距离已知，车辆从规划路线起点的最近的实际公交站场出发，一辆车只能在一条线路运行，每个站点既有上车人数也有下车人数，车辆在站点的停靠时间取决于预约的人数多少，但会有时间惩罚.通过此线路规划模型，在保证利润最大化的基础上，得到k条公交线路的具体路径，从而得到汽车运行的时刻表，也就是每个乘客的上车时间.

基于问卷调查结果的首都高校多集中于学院路或昌平区大学城，因此上车地较为集中，满足式(4)的运行路线不会太长.假期的目的地多是景区，因此有式(5)保证所有点都最终到达景区或者火车站的约束.假期中学生对于准时性不太敏感，因此式(9)的惩罚系数取值相对于普通的定制公交较小.

目标函数：

(4)

约束条件：

(1)保证每个停靠点均被服务(人数较多的点，服务次数大于1[2])：

(5)

(6)

(2)保证所有点都最终到达景区或者火车站，设置站点0为景区或者火车站：

(7)

(3)保证车辆载客数不超过车辆的最大载客量：

(8)

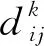
(4)时间窗约束：

去景点，软时间窗：

(9)

去火车站，硬时间窗：

(10)

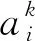
(5)最低上座率要求[8]：

(11)

式中，rmin表示最低上座率.

(6)约束条件：

园里最先开花的是刺玫和丁香，刺玫在有刺的枝干保护下，开着粉红花朵，羞涩地躲在满是尖刺的枝干中，让人可爱不可及。相比之下，丁香花显得大方，花烃出枝很高，雪白色的花瓣散着芳香，沁人心脾，一眼望去，整个树被花包围着，几乎看不到叶子，与旁边的沙果，李子树开的花相辉映，构成一幅花海乐园。

(12)

2.3 线路规划模型求解

遗传算法适合求解离散问题，具备数学理论支持，但存在着汉明悬崖等问题；粒子群算法适合求解实数问题，算法简单、方便，求解速度快，但存在陷入局部最优等问题；蚁群算法适合在图上搜索路径问题，它作为元启发式算法，是一种算法框架，可以在其基本思想上针对不同问题做改进从而应用到不同问题上去，同时蚁群算法考虑因素全面，收敛速度快，因此本文的问题运用蚁群算法也就最为合适.选取经典的蚁群算法进行求解，并在原有基础上进行改进.

(a) 挥发函数a (b) 挥发函数b (c) 挥发函数c图3 信息素浓度和挥发系数函数关系图

各个需求点之间的距离构成距离邻接矩阵，随机形成第一种公交运行方案，更新信息表，反复迭代多次得到满意解.

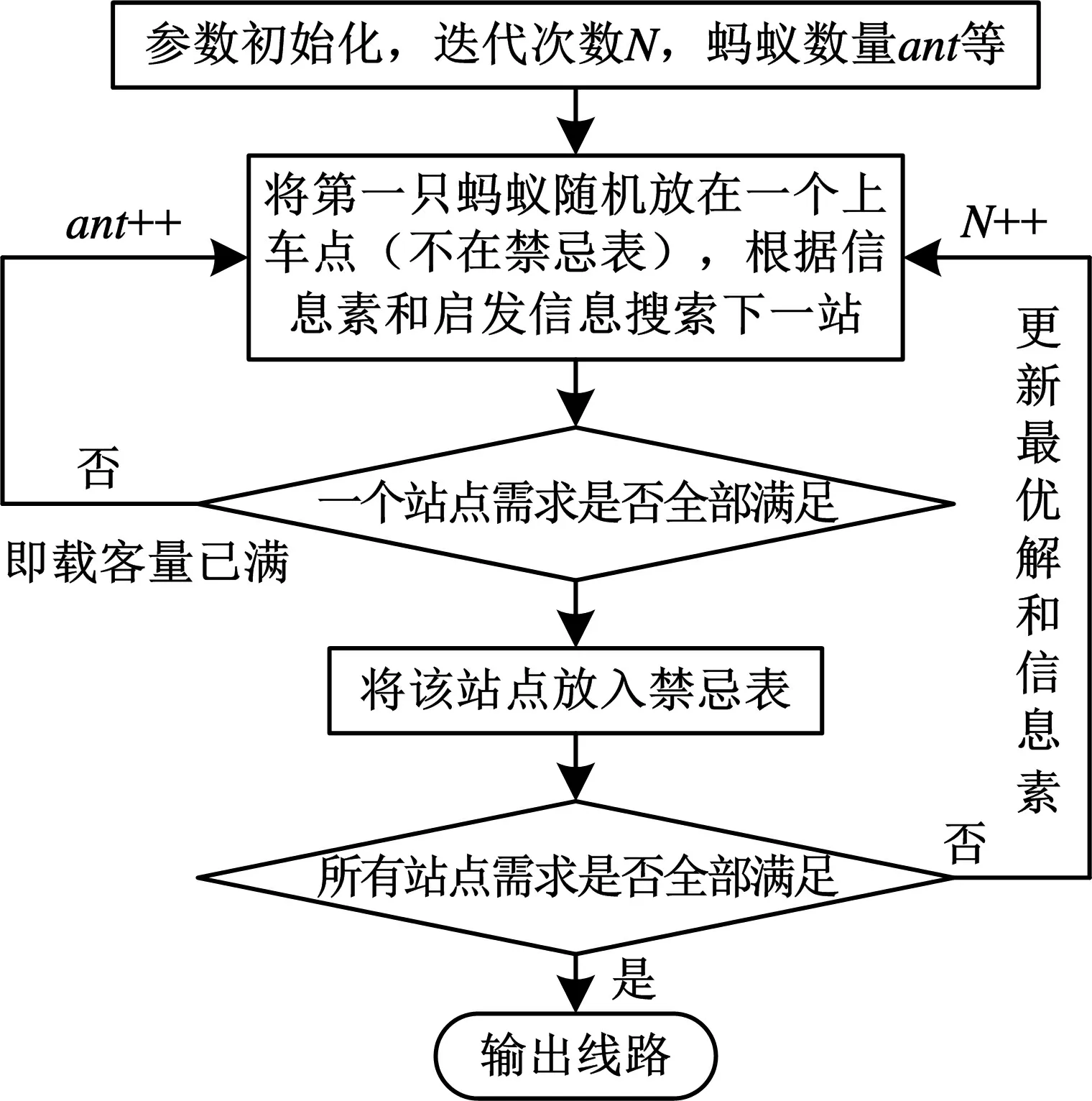
在基本蚁群算法中，对信息素的强度没有限制，因而易陷入局部最优点.改进的蚁群算法对信息素的强度给予一定的限制，从而大大改善了算法的性能.信息素挥发函数对算法的性能有直接的影响，在实验中曾试过如图3所示的3种类型函数(X轴为信息素浓度，Y轴为挥发系数)[9].在信息素启发因子α=1，期望启发因子β=2，最大迭代次数Z=1 000等其他条件都相同的条件下，对于三种信息素挥发函数进行对比，如表1.通过比较，发现信息素挥发函数c在最优路径长度和迭代次数上都优于信息素挥发函数a、b,因此采用信息素挥发函数c,具体求解过程[10]如图4.

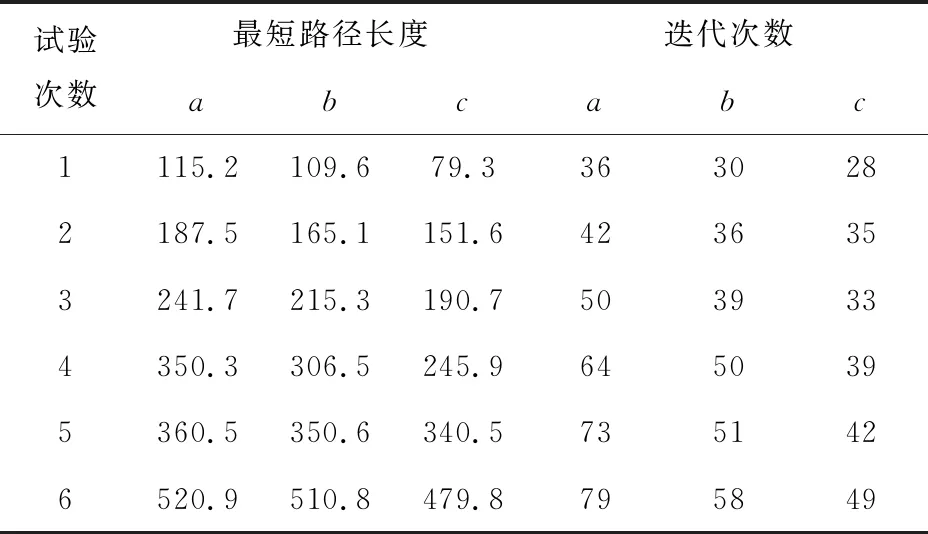
表1 三种信息素挥发函数对比

图4 求解过程

3 案例分析

根据初期的问卷调查数据，选择由北京市高校前往北京西站的大学生出行需求数据作为研究案例，进行高校定制公交时间聚类、站点规划和线路规划的研究，验证了本文所述算法的有效性.首先，通过K-means 算法对学生们的出行数据进行聚类分析，先通过时间聚类，获得两个聚类簇，通过调查问卷8∶00～10∶00的数据随机抽选了80个需求点，然后通过站点聚类，得到上车点19个，如表2所示，这些上车点地图的相对位置如图5所示.

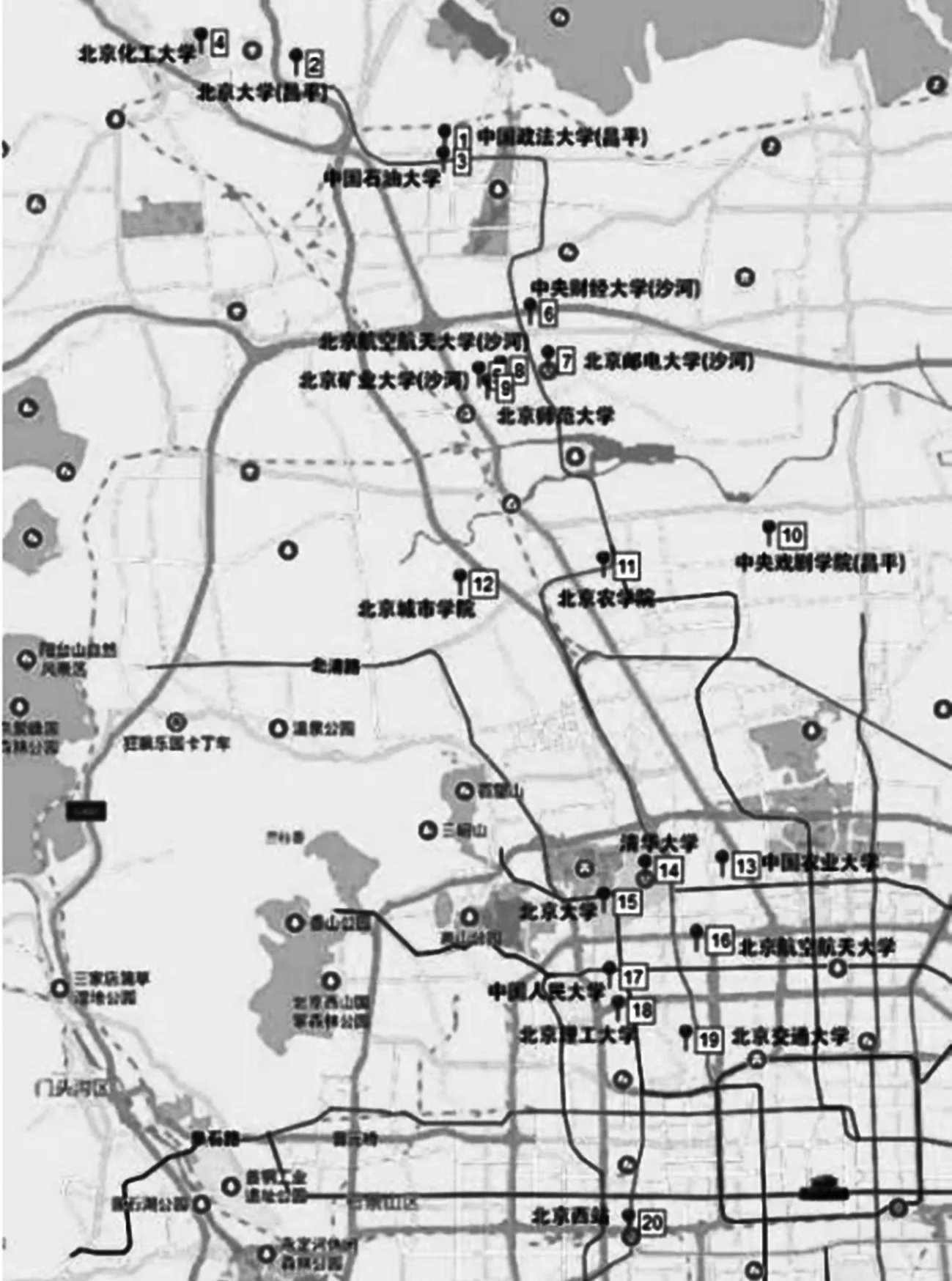
图5 聚类后的站点位置图

表2 上车点及上车人数

算法参数为：种群数为20,迭代次数取1000，信息素强度为0.1.这19个上车点包括终点北京西站，每两个点之间的距离通过电子地图获得.

定制公交最大载客量取普通大巴的平均容量，为45人.在定制公交角度定义上座率等同于一般公交的满载率，从服务水平和收益性角度出发，根据文献[11]提供的平峰高峰满载率等级，选取中值0.75作为A等最低上座率要求.使用本文的算法进行求解，最终得到的定制公交线路规划方案如表3.如图6为定制公交线路在地图的具体路线.其中浅色线路为线路1，深色线路为线路2.

表3 定制公交线路方案

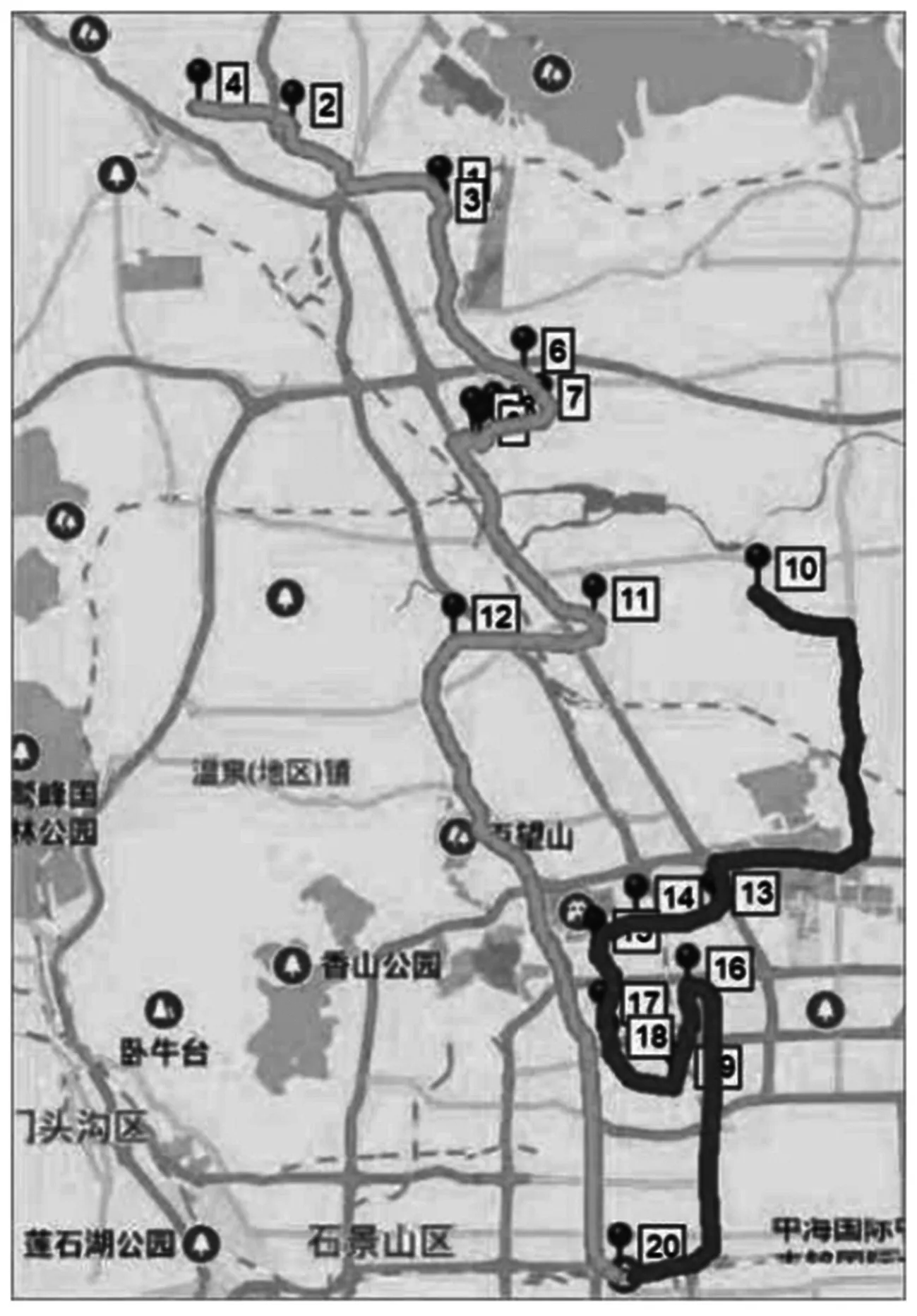
图6 规划线路的具体路线

从运行结果可以看出，两条线路几乎均等地分配了所有需求点，且上座率高达91%和87%.解决了以往定制公交线路覆盖率低，上座率低且运行效率不高的问题，实际的需求响应落实较好，两条线路的能力得到充分应用.优于传统定制公交选择出行需求聚集性高的线路，充分考虑到乘客的时间出行差异，满足了大部分乘客的需求，也增加了经济收益.

4 模型实际应用

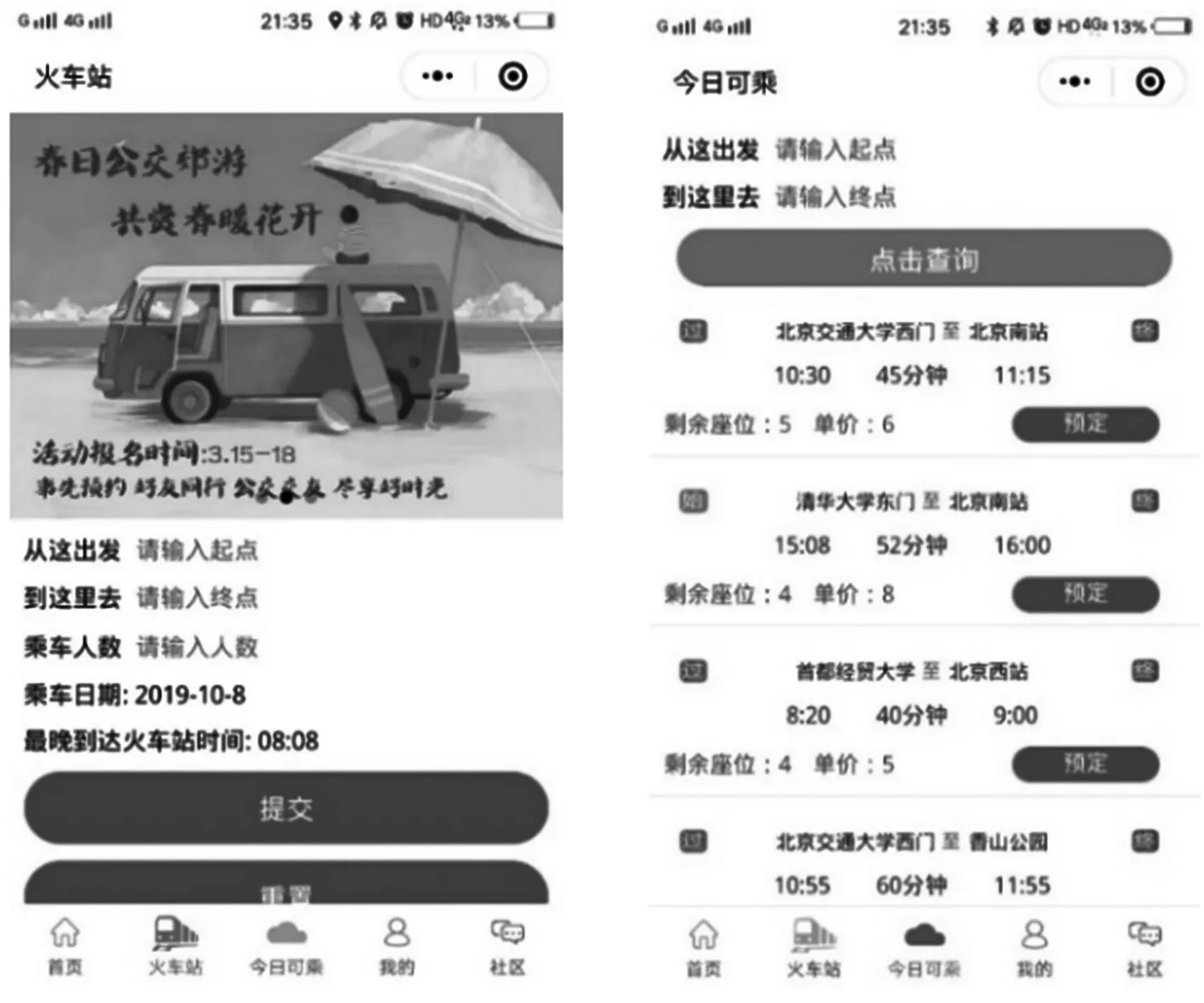
(a) 预约页面 (b) 查询路线页面

(c)社交页面 (d) 预定成功页面图7 定制公交小程序界面

5 结论

通过对大学生出行行为与定制公交关系的研究，可以看出大学生群体对定制公交有着很大的潜在需求，但这部分需求在大众群体中往往被忽略，导致定制公交大学生市场空缺，因此针对特定人群的定制化研究显得很有必要.

确定目标人群大学生后，结合该人群行为特征及分布状况，构建特定的线路规划模型，利用改进的蚁群算法进行求解，可以得到较高的上座率，与现有的定制公交线路规划模型对比有明显效果，可见人群专一化以后不仅提高了运行效率，也增加了经济收益.同时，针对年轻人特点，在应用小程序层面提供了社交功能，凸显了用户专一化的服务优化，即如果不针对特定人群，这一社交功能将很难开展.

因此，本文以大学生群体作为切入点，进行具体的定制公交线路规划模型及算法研究，并提出一定的应用改进，为定制公交用户专一化深入研究提供思路.