基于内力法的伺服弹性快速计算方法
2021-07-27李哲崔高伟王鹏辉谷迎松洪良友孙颖
李哲 崔高伟 王鹏辉 谷迎松 洪良友 孙颖
基于内力法的伺服弹性快速计算方法
李哲1崔高伟1王鹏辉1谷迎松2洪良友1孙颖1
(1 北京强度环境研究所,北京 100076;2 西北工业大学航空学院,西安 710072)
对于带有飞行控制系统的飞行器,当其控制系统与结构弹性变形发生耦合时,会引起伺服弹性问题,直接影响飞行安全与品质。近年来,带有翼舵的飞行器凸显了结构柔性,激光和光纤类传感器提高了控制带宽,使得伺服弹性问题日益突出,给飞行器控制系统设计工作带来了挑战。鉴于此,采用分层求解,逐级验证的思路,建立了以内力法驱动的伺服弹性分析模型,并通过了地面伺服弹性试验结果的验证。相比ZAERO伺服弹性频域分析方法,该方法具有相同的精度,并可将伺服弹性计算效率提高75%。
伺服弹性模型;内力法;伺服弹性试验;频域方法;计算效率
0 引言
伺服弹性(SE)是气动伺服弹性(ASE)多场耦合稳定性问题的一个分支学科,涉及结构、控制、伺服等多个专业[1-3]。控制系统设计的初衷是通过传感器接收到的刚体运动信号控制飞行器飞行。但是,当结构弹性振动信号没有得到恰当处理,参与了飞行器控制时,会导致控制系统稳定裕度降低,影响飞行安全。民用航空等行业对气动伺服弹性幅值裕度、相位裕度都有严格的规定[4],为了考核飞行控制系统的性能及支持气动伺服弹性模型的修正,必须开展飞行器的地面伺服弹性试验[5,6]。在控制系统优化设计时,需要一种伺服弹性快速计算方法来减少迭代次数,缩短设计周期。
20世纪50年代初,随着导弹武器大量应用自动控制技术,伺服弹性问题开始出现[7]。起初发展的是基于气动伺服弹性运动方程的频域方法[8,9],分别得到舵机环节、结构环节、气动力环节、传感器环节和控制器环节的传递函数,利用经典控制理论Nyquist方法判断系统稳定性。后来,国外发展了一套基于现代控制理论的状态空间时域方法,即将前述的各个环节改写成状态空间形式,由于将频域气动力系数延拓至状态空间的拟合方法不同,出现了不同的线性系统状态空间建模方法,常见的有最小状态法、最小二乘法[10-12]、修正矩阵法和拟合状态空间法[13-15]。该类时域方法不仅可以解决单输入单输出(SISO)系统的稳定性问题,还可以开展多输入多输出(MIMO)系统的稳定性分析。此外,国内学者研究了一种基于CFD/CSD耦合计算的气动伺服弹性系统建模方法[16]。同期,为了将研究成果推广到工程应用,国外涌现了一大批气动伺服弹性分析程序,如1)ISAC;2)ZAERO;3)FLEXSTAB;4)NASTRAN[17];5)DYLOFLEX;6)ADAM;7)STARS;8)I-DESIGN;9)NEW SUMT-A等[18]。由于这些程序都是以气动伺服弹性运动方程为基础的,气动力建模是必不可少的一环[19],在单纯进行伺服弹性分析时,为了消除气动力的影响,工程上常将动压项置于接近于0的系数,因此,降低了伺服弹性计算效率。国内学者从频域气动弹性方程出发,将结构模态信息与气动力系数矩阵作为原始输入数据,编制了相关气动伺服弹性分析程序,并已应用在一些实际工程分析中。近年来,国内学者开展了一些非线性气动伺服弹性建模与降阶工作,并取得了一些研究成果[20-22]。
为了提高伺服弹性模型建模和计算分析效率,优化分析模型的规模,以带SISO控制系统的飞行器为研究对象,首先从结构环节的传递函数入手,通过内力法获取结构环节的传递函数。依托伺服弹性耦合机理,摒弃了以往模型中冗余的气动力环节,建立了由控制环节、舵机环节、传感器环节与结构环节组成的伺服弹性系统模型与分析流程。然后,通过数值算例分析了影响飞行器伺服弹性的关键模态及各环节灵敏度。最后,通过地面伺服弹性试验验证了模型的精度,同时,结合ZAERO伺服弹性频域分析方法,对比分析了计算效率,并给出了相关结论。
1 系统模型
目前飞行器增稳控制系统多采用负反馈闭环回路[23],其ASE系统如图1所示。其中,气动力AIC矩阵的获取需要大量的时间去建模与计算。在考虑伺服弹性建模分析时,不妨将气动力环节删除,建立如图2所示的SE系统,开展SE分析。
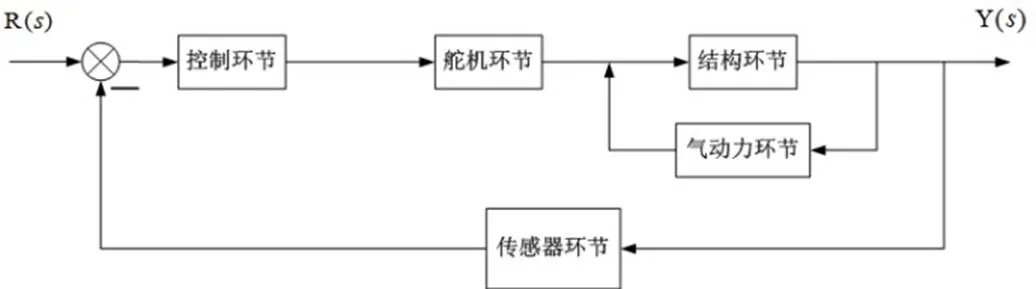
图1 ASE系统模型
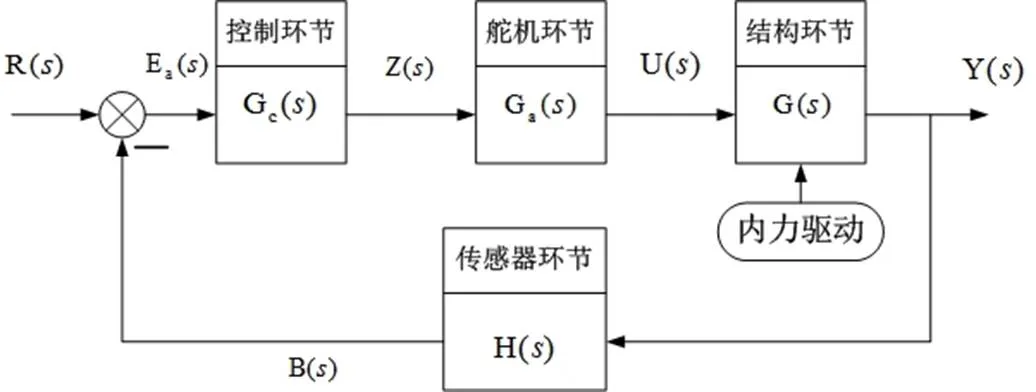
图2 SE系统模型
上述负反馈SE系统的控制环节激励信号遵循下面的方程
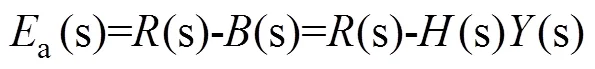
由控制环节、舵机环节、结构环节的传递函数可得到输出信号与激励信号的关系式如下
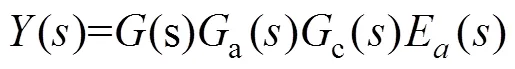
将式(1)与式(2)联立可解得

式(3)即为SE系统闭环传递函数。在应用经典控制理论来进行SE分析时,难点是结构环节传递函数的获取。与以往通过结构频响分析获取结构传递函数的区别有两点,一个是伺服弹性分析的输入条件为舵机驱动的舵面偏转信号,而不是常规的外激励。另一个是结构不受外力作用。为满足上述两点要求,本文在建立结构体系的运动方程时,在作动杆结点处,采用一对内力(大小相等,方向相反,作用在同一作用线)来给节点载荷列阵赋值,以模拟舵面控制偏转,可得到SE分析时所需的运动方程,即
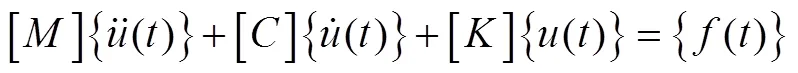
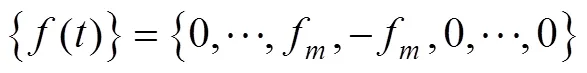
对式(4)进行拉普拉斯变换,可得到运动方程的频域表达式[24]
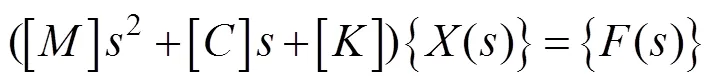
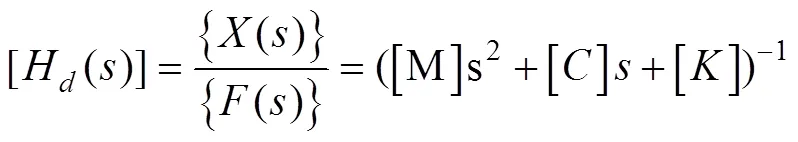
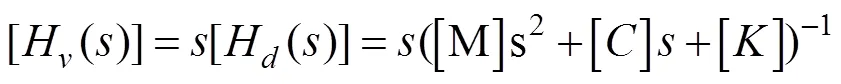
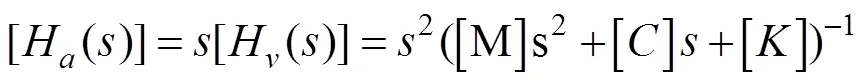
利用模态的正交性与阻尼解耦假设可得
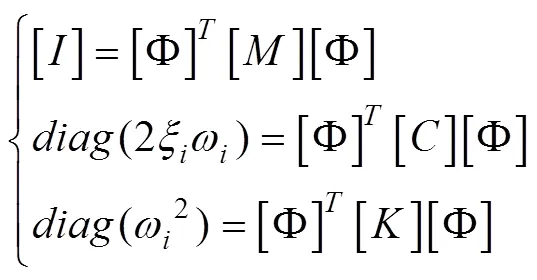
由式(10)可得结构质量阵、阻尼阵、刚度阵的表达式为
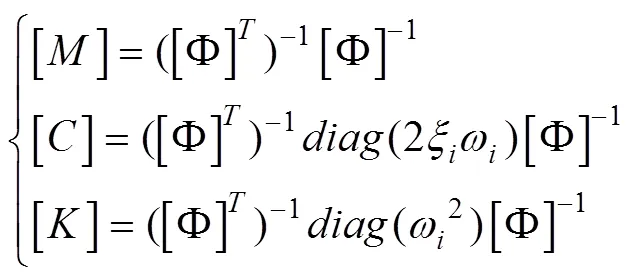
将(式11)带入式(7)~(9)可得系统的位移、速度、加速度的传递函数
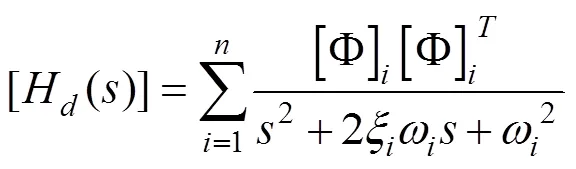
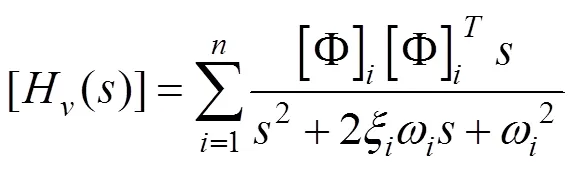
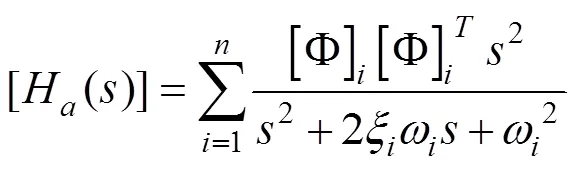
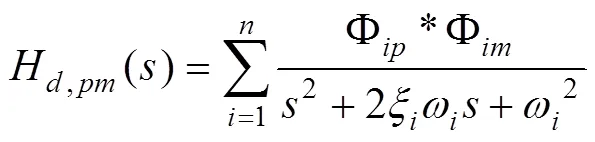
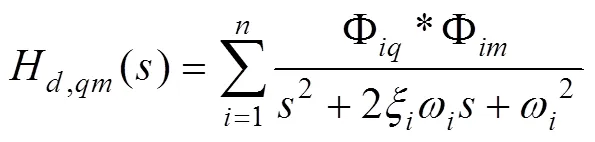
2 数值算例
2.1 分析模型
按照“梁+壳+集中质量”的建模思路,建立了飞行器的三维动力学模型,传感器安装区局部结构及尾舵伺服系统处结构的有限元模型如图3所示,内力施加在尾舵作动杆上。增稳控制系统采用角速率负反馈,左右尾舵用于飞行器的俯仰通道控制。
2.2 基于内力法的伺服弹性分析
2.2.1 开环传递特性
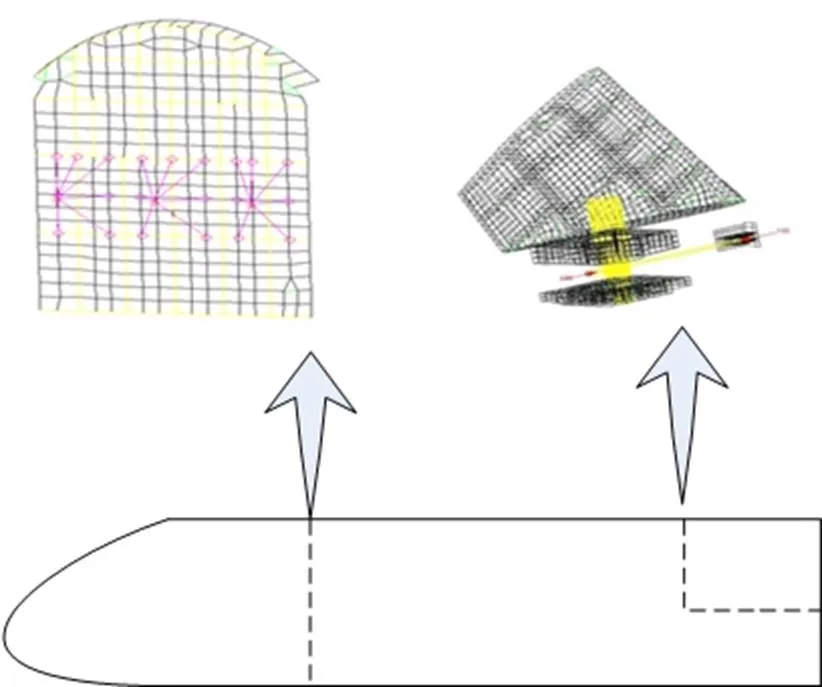
结合结构动力学有限元模型,基于内力法开展结构频响分析,获得结构环节传递函数,分别与通过系统辨识得到的舵机环节、传感器环节串连,可得到舵系统传递特性、传感器处的传递特性。传感器安装框端面处传递特性如图4所示,此处提取了环向40个节点的结果,传递曲线基本重叠,验证了模型的一致性。从传递曲线上可以看出,尾舵弯扭耦合模态是降低系统稳定裕度的主要原因。
(a)传感器安装区(b)尾舵伺服系统
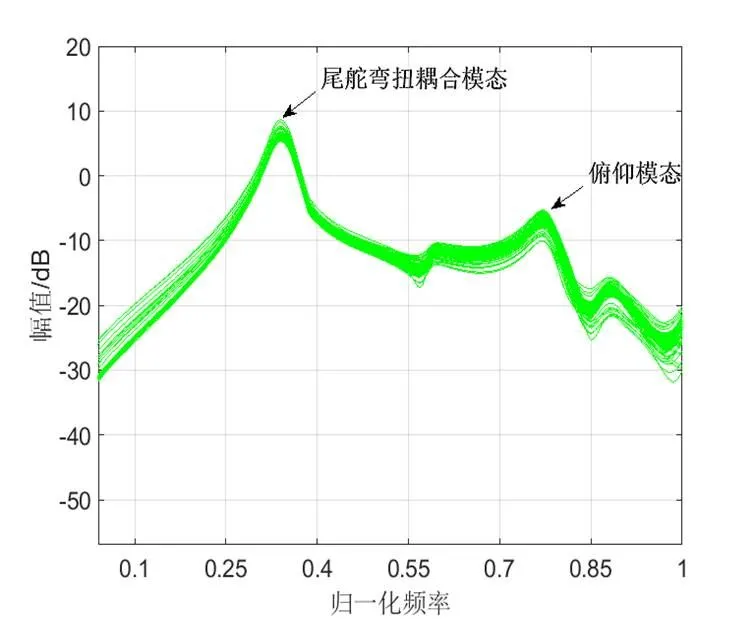
图4 传感器安装框端面处传递特性
2.2.2 闭环稳定性
在上节的结构开环传递特性的基础上,串连飞控环节的传递函数,应用经典控制理论Nyquist判据,判断系统稳定性,俯仰通道幅值裕度为5.1dB,相位裕度为38位,Nyquist图如图5所示。
图5 系统Nyquist图
2.3 灵敏度分析
为了开展伺服弹性优化设计,需要量化各环节对闭环系统稳定裕度的影响。分别从伺服环节的传递函数频率偏差、结构环节的模态频率偏差、传感器环节的指令参数偏差出发,设置3类单一变量分析工况。同类工况中相邻2个工况的偏差变化量相同,纵坐标为幅值裕度,则斜率大小可表示灵敏度。从计算结果可以得出结构环节的模态频率偏差对幅值裕度影响最大,稳定裕度散点图如图6所示。
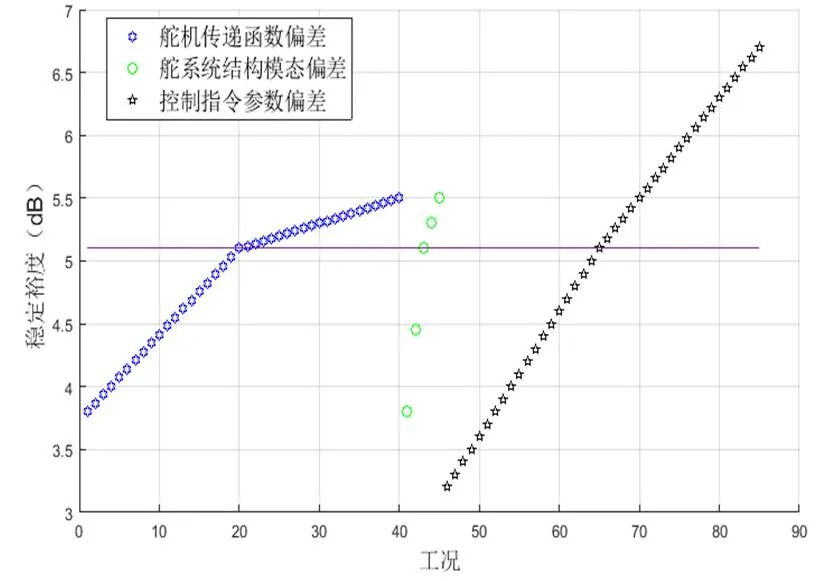
图6 稳定裕度散点图
3 试验验证与对比分析
3.1 开环传递试验
开环伺服弹性试验需要先将控制组合与伺服控制驱动器断开,使系统处于开环状态,将飞行器所有伺服、惯组和飞控计算机连接到1553B总线上。开环传递试验原理图如图7所示。利用地面总线测试仪,向伺服控制驱动器发送舵偏指令信号,控制舵机进行连续正弦扫描驱动舵面运动,实现伺服弹性开环激励,通过同步测量激励和响应,来分析获取各环节的开环传递函数,扫频范围为2Hz~50Hz。
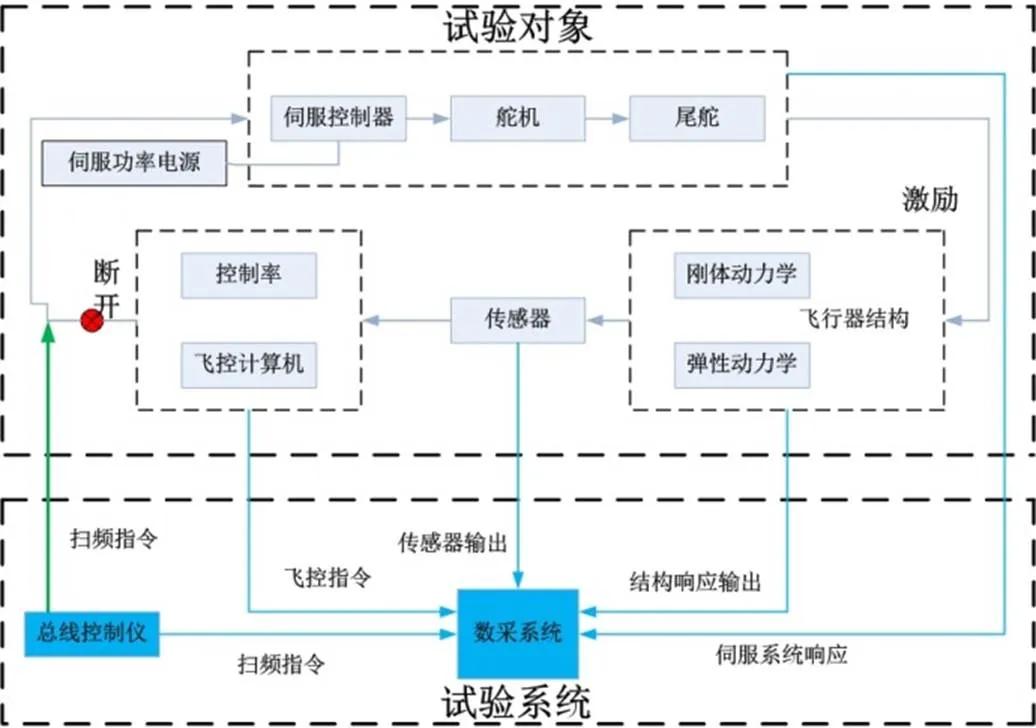
图7 开环传递试验原理
3.2 闭环稳定性试验
闭环稳定性试验需要将控制组合与伺服系统连接后处于闭环状态,控制系统装订飞行控制参数,开始实时控制解算,并对受到的扰动作出响应。在每个试验状态下,控制参数固定不变。激励方式分两种进行,一种是通过在伺服指令输入端加入脉冲激励信号,模拟舵系统工作时惯性力影响。第二种对飞行器进行外部力激励,模拟飞行时的干扰力影响。本试验采用第一种方案,闭环稳定性试验原理图如图8所示。在伺服指令中加入三角脉冲激励信号,叠加后再作用到伺服控制驱动器上,控制舵面产生偏转,同时采集舵面和传感器等响应,并监测飞行器结构的振动情况。试验中,如果系统稳定,则逐级加大控制律增益,直到出现不稳定,以此验证飞行器伺服弹性系统的稳定性和稳定裕度。
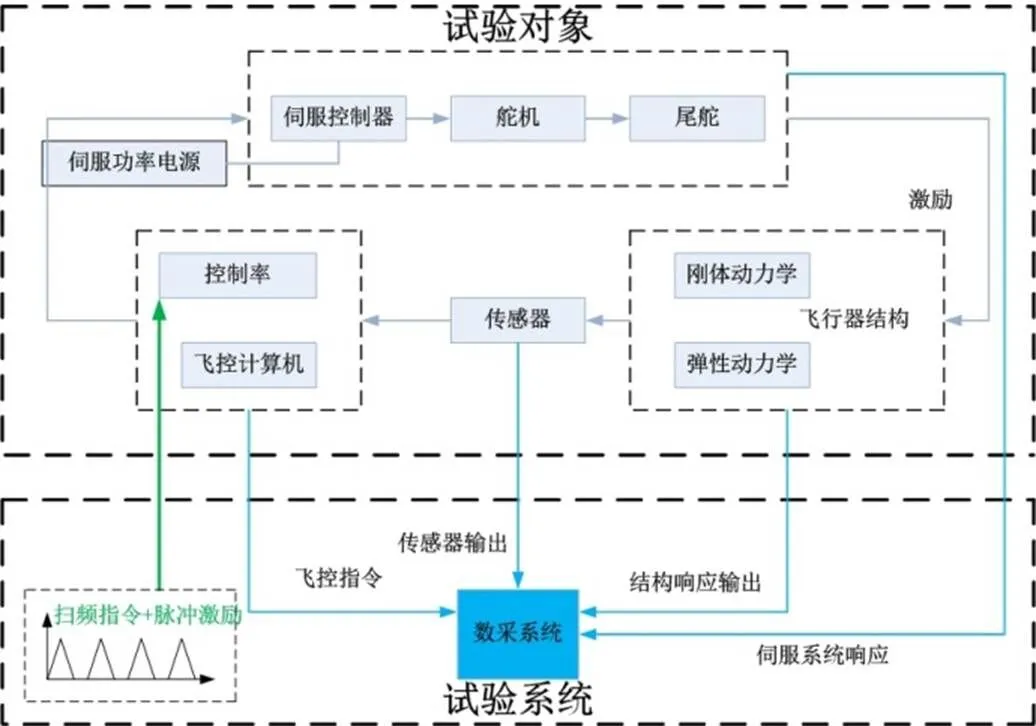
图8 闭环稳定性试验原理
3.3 对比分析
为了开展算法对比分析,利用ZAERO商业程序编制了相同的控制系统,其控制系统卡片如图9所示。
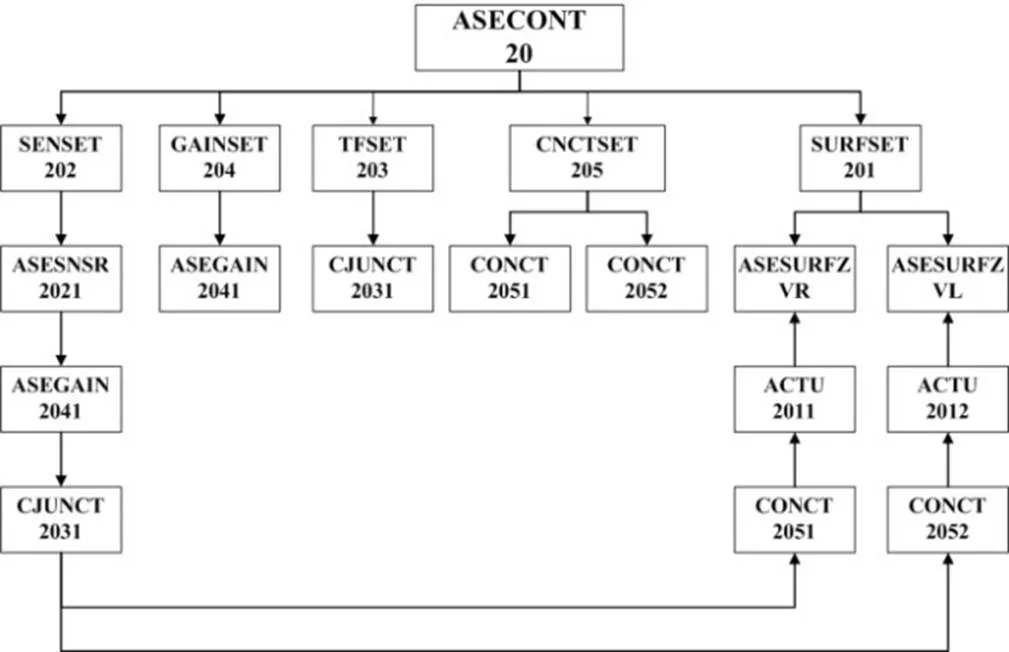
图9 ZAERO控制系统卡片
将伺服弹性试验结果、内力法获得的伺服弹性结果、ZAERO计算结果列于图10。从传递特性的对比结果来看,三种方法得到的飞行器传递特性趋势相同,都可以找出系统内信号放大的原因,基于内力法计算得到的伺服弹性结果偏保守。
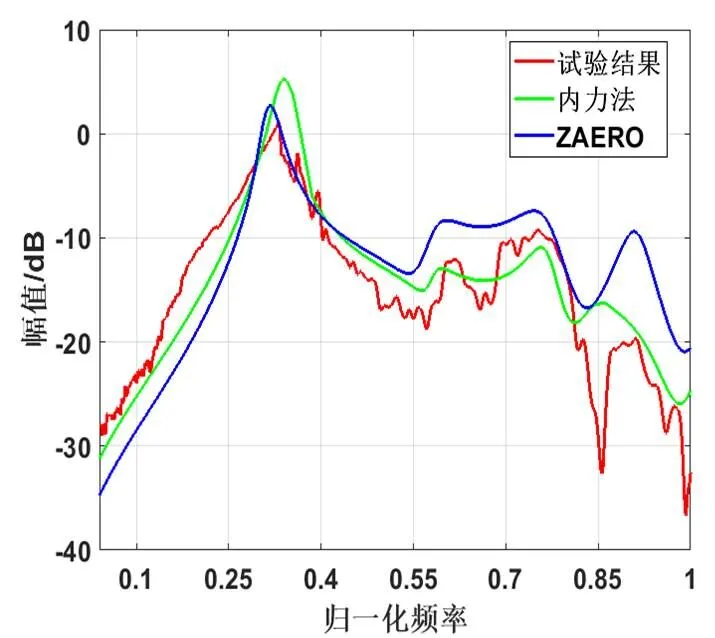
表1给出了内力法及ZAERO软件在计算效率方面的数据,内力法需要开展频响分析、SE分析,CPU共计耗时357s;ZAERO需要开展模态分析、模态数据导入、气动插值、ASE分析,CPU共计耗时1443s。内力法的计算效率相较ZAERO算法可提高75%。
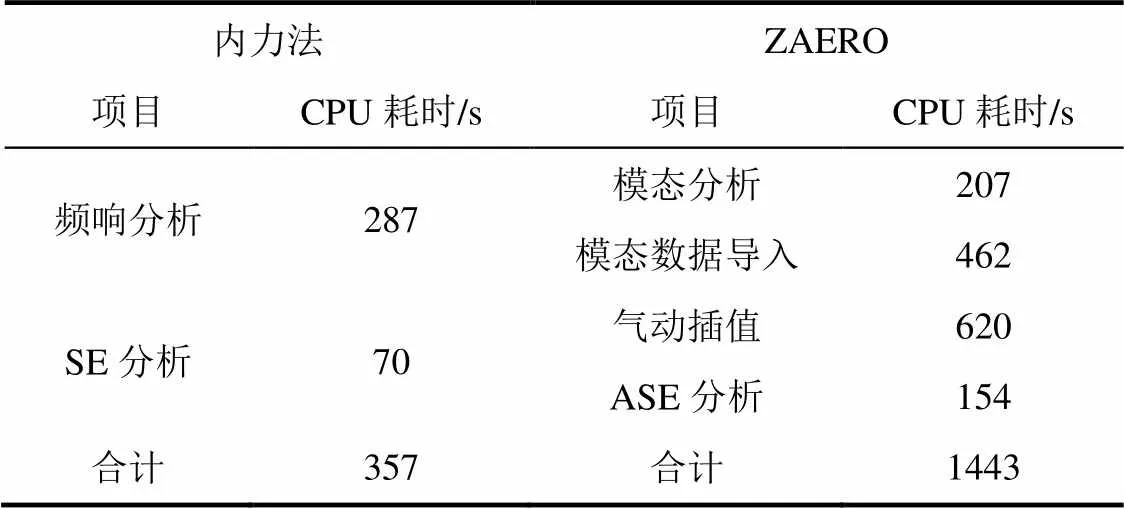
表1 计算效率相关数据
4 结论
本文提出了基于内力法的伺服弹性分析模型,建立了其分析流程,通过地面伺服弹性试验验证了模型的准确性,与ZAERO伺服弹性分析方法相比,计算效率可提高75%。从变参数值算例结果来看,模型的一致性较好,影响飞行器俯仰通道稳定性裕度的关键模态有尾舵弯扭耦合模态和俯仰模态。此外,模态频率偏差对裕度分散性影响较大,需引起控制系统设计单位的重视。由于Nyquist经典控制理论的使用条件所限,尚未考虑复杂的控制系统,因此有待深入开展MIMO控制系统的飞行器SE稳定性分析方法研究。另外,将气动力环节引入本文分析模型形成ASE闭环分析系统也值得进一步研究。
[1] Karpel M.Procedures and models for aero servo elastic analysis and design [J].Journal of Applied Mathematics and Mechanics, 2001,81(9): 579-592.
[2] Gupta K K, analysis Meek J L.Finite element multi disciplinary analysis[M].2nd ed.Reston: AIAA, 2003: 295-310.
[3] Yang C, Wu Z G, Wan Z Q, et al.Principle of aircraft aero elasticity [M].Beijing: Beihang University Press, 2011: 148-167.
[4] 丁路宁, 范石磊, 陈磊.客机伺服弹性特性研究[J].航空科学技术.2018(29): 21-24.[DingLuning, FanShilei, ChenLei.Servoelasticresearchofcivilairplane[J].Aeronautical ScienceTechnology, 2018, 29(S1): 21-24.]
[5] 李慧娜, 高庆, 肖健, 等.空气舵-伺服系统动态特性试验技术研究[J].强度与环境, 2013(4): 7-11.[LI Huina, GAO Qing, XIAO Jian, et al.The study of rudder-servo system dynamic test technique[J].Structure & Environment Engineering, 2013(4): 7-11.]
[6] 周礼洋, 冯颖川, 左祥昌, 等.V尾伺服弹性试验失稳定位方法研究[J].强度与环境, 2015,42(3): 21-27.[ZHOU Liyang, FENG Yingchuan, ZUO Xiangchang, et al.Study of unsteady location approaches for V-tail servo-elasticity test[J].Structure & Environment Engineering, 2015,42 (3): 21-27.]
[7] Felt I R, Huttsell I.J, Noll T E, et al.Aeroservo elasticen counters [J].Journal of aircraft, 1979, 16(7):477-483.
[8] ZONA Technology.Zaero theoretical manual[M].US: ZONA Technology, 2008.
[9] 杨超, 吴志刚, 万志强, 等.飞行器气动弹性原理[M].北京: 北京航空航天大学出版社, 2011.
[10] Noll T E.Aeroservo elasticity[R].AIAA 90-1073, 1990.
[11] 邹丛青, 陈桂彬.气动弹性力学的新分支-气动伺服弹性[J].北京航空航天大学学报, 1995,21(2): 22-27.[Zou Congqing, Chen Guibin.A new branch of aero elasticity-aeroservo elasticity[J].Journal of Beijing university of aeronautics and astronautics,1995, 21(2): 22-27.]
[12] 宗捷.非定常空气动力有理函数近似及非线性颤振研究[D].北京: 北京航空航天大学, 1995.
[13] Pitt D M, Goodman C E.FAMUSS: a new aeroservo elastic modeling tool[R].AIAA-92-2395,1992.
[14] 陈立新.用于气动伺服弹性的低阶建模方法及其应用研究 [D].北京航空航天大学, 1997.
[15] 宋晨, 杨超, 吴志刚.3种气动弹性状态空间建模方法的对比[J].航空学报, 2007, 28(S1): S82-S86.[ SONG Chen, YANG Chao, WU Zhi-gang .Comparison of three aeroelastic state-space modeling methods[J].Acta Aeronautica Et Astronautica Sinica, 2007,28(S1): S82-S86.]
[16] 陈刚, 徐敏, 陈士橹.非定常气动力状态空间模型及其在气动伺服弹性建模中的应用[J] 空军工程大学学报, 2004,5(5): 1-4.[Chen Gang, Xu Min, Chen Shilu.State space model of unsteady aerodynamics and its application to aero-servo-elasticity[J].Journal of Air Force Engineering University, 2004,5(5): 1-4.]
[17] Rodden W P, Johnson E H.MSC'/NASTRAN aeroelastic analysis user’s guide [M ].Version68.LosAngeles MacNeal-Schwendler, 1994:7-132.
[18] Rodney H R, Thanas E N, Woodrctn W et al.An overview of aero elasticity studies for the national aero-space plane[R].NASA TM 107728, 1993(3).
[19] 徐敏, 李勇, 曾宪昂, 等.基于Volterra级数的非定常气动力降阶模型[J].强度与环境, 2007(5): 22-28.[ XU Min, LI Yong, ZENG Xian-ang ,et al.Volterra-series-based reduced-order model for unsteady aerodynamics[J].Structure & Environment Engineering, 2007(5): 22-28.]
[20] 杨智春, 田玮, 谷迎松, 等.带集中非线性的机翼气动弹性问题研究进展[J].航空学报, 2016, 37(7): 2013-2044.
[21] 田玮.高超声速飞行器非线性气动弹性问题研究[D].西北工业大学, 2018.
[22] 谢科.舵面非线性颤振问题的降阶建模分析与软件开发[D].西北工业大学, 2020.
[23] 谢红卫, 孙志强, 宫二玲, 张纪阳.现代控制系统[M].北京: 电子工业出版社, 2015.
[24] 王光远, 等.结构动力学[M].北京: 高等教育出版社, 2006.
A Fast Calculation Method of Servo Elasticity Based on Internal Force
LI Zhe1CUI Gao-wei1WANG Peng-hui1GU Ying-song2HONG Liang-you1SUN Ying1
(1 Beijing Institute of Structure and Environment Engineering,Beijing 100076,China;2School of Aeronautics,Northwestern Polytechnical University,Xi’an 710072,China)
For the aircraft with flight control system, when the control system is coupled with structural elasticity, that will cause servo elasticity problems, directly affecting flight safety and quality.In recent years, the flight control system design has been brought challenges by serious servo elasticity problem that structure flexibility is highlighted by heterosexual aircraft, control bandwidth is increased by laser and optical fiber sensors.In view of that, using the idea of layered solution and step-by-step verification, a servo elasticity analysis model driven by the internal force method is established, which passed the verification of ground servo elasticity test.Compared with ZAERO servo elasticity frequency domain method, the method has the same accuracy and can increase the calculation efficiency by 75%.
Servo elasticity model; internal force; servo elasticity test; frequency domain method; calculation efficiency
V215.3
A
1006-3919(2021)03-0016-06
10.19447/j.cnki.11-1773/v.2021.03.003
2021-03-11;
2021-04-12
XX飞行器气动/热/结构/控制系统祸合振动抑制技术(41410040101)
李哲(1993—),男,工程师,研究方向:结构动力学;(100076)北京市9200信箱72分箱.
