压电多层膜悬臂梁受力的有限元仿真

李苏洋，夏鸿建，张晓伟，陈显锋

（1.广东工业大学机电工程学院，广东 广州 510006；2.佛山市卓膜科技有限公司，广东 佛山 528200）

1 引言

锆钛酸铅（PZT）是MEMS领域应用最广泛的压电材料，因压电系数高、制造工艺相对成熟，可与MEMS结构良好兼容，成形工艺好，价格低等，而得到越来越广泛的应用。悬臂梁是MEMS器件中最常用的微执行机构，具有结构简单、结构尺寸小、灵敏度高、低功耗等特点。对于表面镀有压电薄膜的悬臂梁，由于压电材料具有压电效应，使压电悬臂梁同时具有驱动和传感的特点，其应用前景广阔，成为目前的一个研究热点[1-3]。

在实际设计和加工中压电悬臂梁一般都采用多层复合结构，国内外很多学者建立了微悬臂梁的力学模型[4]，但很少对微梁的变形应力进行研究，特别是固定端的应力。应力是影响MEMS器件疲劳寿命的重要因素，因此对固定端的应力分析很重要[5-6]。现有文献大多是对多层结构薄膜的残余应力进行研究，鲜有文献研究集中载荷对微悬臂梁的固定端应力的影响以及与曲率半径的关系。

以锆钛酸铅（PZT）作为压电薄膜材料，建立了一个多层膜悬臂梁结构，并对其自由端在受到外力F作用下发生的弯曲变形进行了仿真模拟。悬臂梁自由端受到外力后发生弯曲变形，运用ABAQUS有限元软件及梁的力学理论分析梁固定端的应力情况。设曲率半径为ρ，可采用梁理论进行分析，分析微悬臂梁在受不同载荷和薄膜厚度的条件下对曲率半径和固定端应力的影响。

对于悬臂梁的弯曲变形，大多数采用Stoney模型作为理论分析。该理论有如下假设：（1）薄膜及衬底厚度远小于其宽度和长度；（2）薄膜与衬底的厚度比远远小于1；（3）衬底材料是均匀的、各向同性的线性弹性材料，薄膜材料也是各向同性的；（4）悬臂梁的边缘效应可以忽略且弹性性质延厚度方向上平移不变；（5）应力在延厚度方向上没有梯度；（6）系统内部应变及弯曲曲率都很小；（7）不考虑末端效应的影响。它主要用来研究表面镀膜引起的弯曲，而不考虑薄膜厚度影响。但随着制造工艺的发展，衬底的厚度越来越小，使得薄膜厚度与衬底具有了可比性，此时Stoney公式不再适用[7]。

悬臂梁自由端在受到外力F作用下会发生偏转，由于变形很小，视为弹性变形，多层材料复合微悬臂梁弯曲时假设悬臂梁中性层长度不变，各层在轴向弯曲时应变相同，则四层梁结构的挠曲方程可通过静态平衡方程推导出来[8]。此外，悬臂梁的厚度比总体曲率小很多，可假设所有层曲率半径近似等于结构总体的曲率半径。通过仿真与解析模型计算的结果进行比较分析，以验证有限元模型的正确性。

2 模型建立

2.1 有限元模型的建立

压电多层膜悬臂梁自由端受外力F作用后，如图1（a）所示。梁的横截面，如图1（b）所示。悬臂梁结构包括四层，分别为基底层1、过渡层2、电极层3和压电层4，各层材料包括基底层1为聚酰亚胺（PI）、过渡层2为二氧化硅（SiO2）、电极层3为铂（Pt），压电层4为锆钛酸铅（PZT）薄膜。每一层的长度l为1000μm，宽度b远小于长度l及厚度h。各层厚度t分别为t1=25μm，t2=0.5μm，t3=0.2μm，t4有0.1μm，0.5μm，1.5μm和10μm四个水平，总体结构的厚度为h。各层材料的力学性能参数与几何参数，如表1所示。

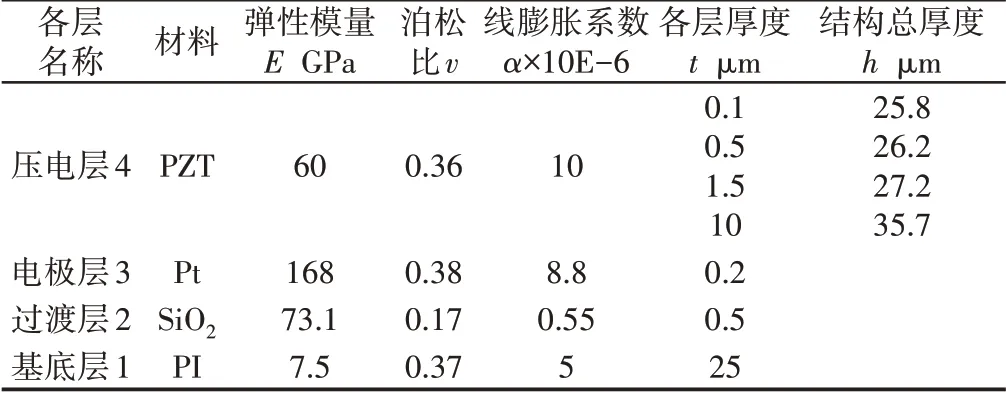
表1 压电多层膜悬臂梁的几何参数和力学参数Tab.1 Geometric Parameters and Mechanical Properties of Piezoelectric Multilayer Cantilever

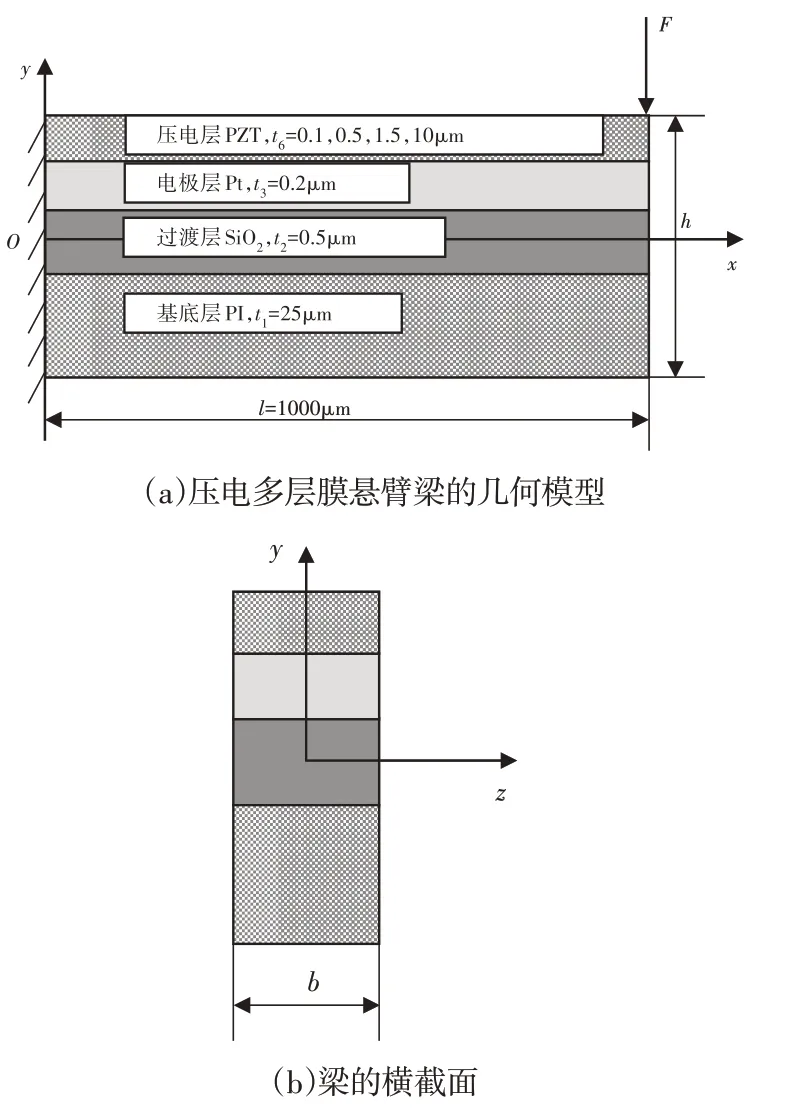
图1 各层材料的力学性能参数与几何参数Fig.1 The Mechanical Property Parameters and Geometric Parameters of Each Layer Material

假设图1的压电悬臂梁宽度远小于长度及厚度，自由端x-y平面内受到集中力作用，不计体力，根据这个结构特点，可作为xy平面内的平面应力问题处理。对于平面应力问题，σz=0，τzy=τxz=0。此时，有限元仿真模型可引入几个假设：（1）不考虑剪切应力的影响（2）梁的宽度及厚度远小于梁弯曲的曲率半径和梁的长度；（3）各层材料在x-z平面内为各向同性，在x-y平面内呈正交各向异性。基于上述假设，压电多层薄膜悬臂梁的自由端在受到外力F作用下，相当于悬臂梁的纯弯曲过程。由于多层材料之间粘接在一起，故认为各层在轴向弯曲时应变相同，每一层的曲率半径等于结构总体的曲率半径。

悬臂梁一端固定，另一端自由弯曲。固定端各层均为固定约束，各层之间的接触定义为tie。由于压电层的固定端应力是特别关注的重点区域，直接影响MEMS器件装置的疲劳损伤及寿命，因此将压电层的单元网格划分得较密以得到较精确的结果，而基底层的网格划得较稀疏以加快计算速度。选择平面应变非协调四边形单元类型。建立的二维有限元模型，如图2所示。

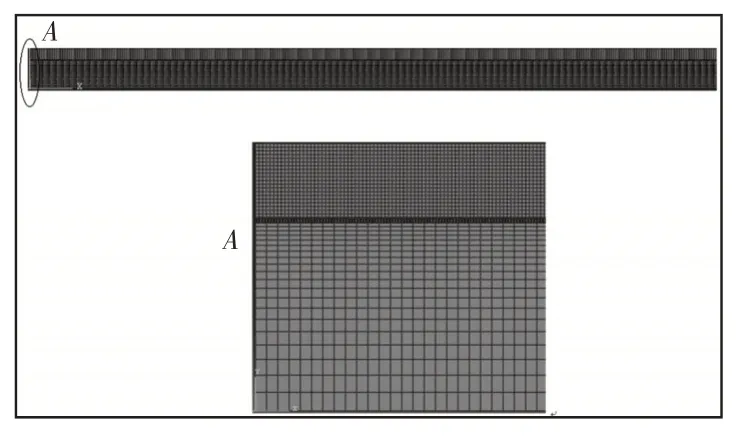
图2 压电多层膜悬臂梁的有限元模型Fig.2 Two-Dimensional Finite Element Model of Piezoelectric Multilayer Cantilever

2.2 理论模型的建立

对于压电多层材料悬臂梁，当其自由端受到y轴方向的压力F，可等效为在末端受到一个弯矩M（x）及一个与外力平行的剪力F（Q）。考虑到悬臂梁的长度l与薄膜厚度之比l/h＞＞5，剪力的影响很小，可忽略不计，梁的横截面上的正应力分布与纯弯曲时很接近。纯弯曲状态下，薄膜中性层上方受到拉伸应力，中性层下方为压缩应力，且悬臂梁的各个截面处应力分布与该点到中性轴的距离成正比。梁发生弯曲变形，其变形示意图，如图3所示。梁在固定端附近的变形最小，在自由端处的变形最大。根据材料力学方程，在坐标x处，距离中性轴的纵向坐标为y时，弯曲应力σx为：

图3 压电多层悬臂梁弯曲变形示意图Fig.3 Bending Deformation Diagram of Piezoelectric Multilayer Cantilever

将式（1）代入式（2）中，得到曲率半径的计算公式：

式中：E′—多层平均弹性模量；y—距中性面的y向坐标；ρ—悬臂梁弯曲变形后任意一点的曲率半径；M（x）—悬臂梁距离原点x处的力矩；Iz—此截面相对于中性轴的惯性矩且l，b，h—微悬臂梁的长度、宽度和厚度。

对于多层平均弹性模量E′，如式（4）所示。

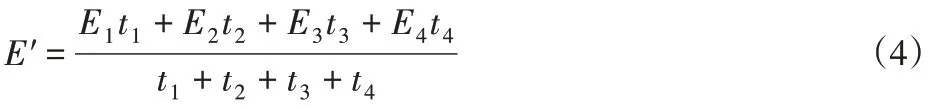
其中E1，E2，E3和E4分别为基底层、过渡层、压电层和薄膜层的弹性模量，t1、t2、t3和t4分别为各层薄膜的厚度[9]。由此可得多层微悬臂梁在不同层厚时的平均弹性模量E′，如表2所示。

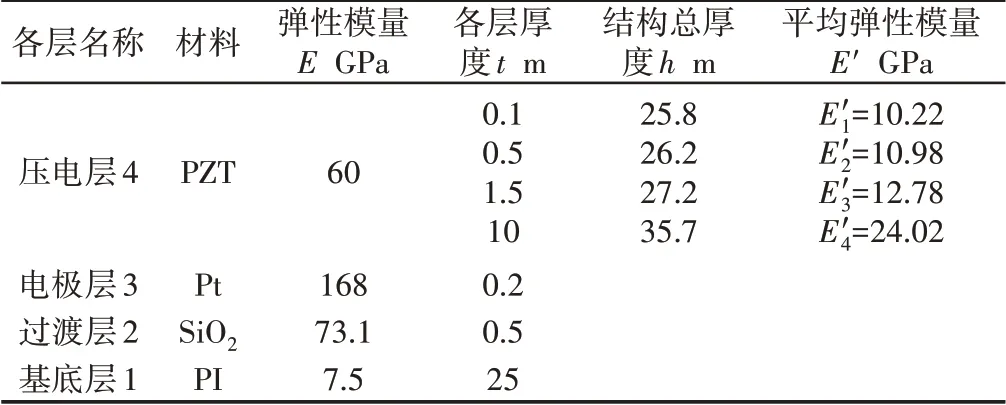
表2 压电多层膜悬臂梁不同厚度时的平均弹性模量Tab.2 Average Elastic Modulus of Piezoelectric Multilayer Cantilever Beam with Different Thicknesses

由式（1）可知，当截面所受的弯矩M（x）和到中性层距离y值为最大时，可得最大弯曲正应力为：

可见，微悬臂梁最外缘处的最大应力与弹性模量无关，而与悬臂梁所受的载荷与截面形状有关。

由材料力学和高等数学的相关知识，可导出挠曲线微分方程的一般形式[10]：

对于加载力F集中在自由端的悬臂梁来说，其边界条件为y(l)=0，y′(l)=0。则微分方程（6）可变形为：

由式（7）可知，力F与挠度y（x）为线性关系，设固定端x=0，则当x=l时，挠度y（x）取得最大值ymax：

可导出曲率半径方程[11]：

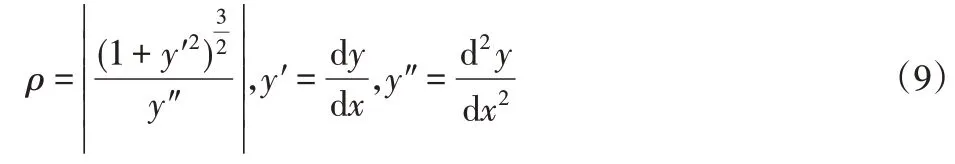
值得注意的是，上述方程适用于小变形情况，当加载力超过一定程度时，加载力与挠度不再呈线性关系。

3 仿真模拟与理论结果比较

悬臂梁自由端受到外力发生弯曲变形，此时压电层固定端应力是关系到MEMS器件寿命的重要因素。为了研究悬臂梁曲率半径与压电层固定端应力的关系，针对同一基底材料，不同压电层PZT厚度进行了数值仿真模拟分析。通过比较不同膜厚在外力F作用下对最大挠度ymax和固定端等效应力的影响，尽量使悬臂梁最大挠度最大化，等效应力最小化，以得到灵敏度更高，使用寿命更长和使用范围更广的悬臂梁MEMS器件。

3.1 挠度y与载荷F的关系

根据表1的几何和材料参数，可得多层悬臂梁自由端在载荷F作用下，悬臂梁各处的变形仿真结果，如图4所示。可见，多层悬臂梁最上层的自由端附近发生的变形最大，基底层的变形最小。根据理论式（8）和表2的几何与材料参数，利用MATLAB软件计算可得悬臂梁自由端最大挠度的解析解，并与仿真结果进行比较，如图5所示。

图4 压电多层悬臂梁自由端受载后各层的变形仿真结果Fig.4 Simulation Results of Deformation for Various Layers under Concentrated Force at the End of Piezoelectric Multilayer Cantilever

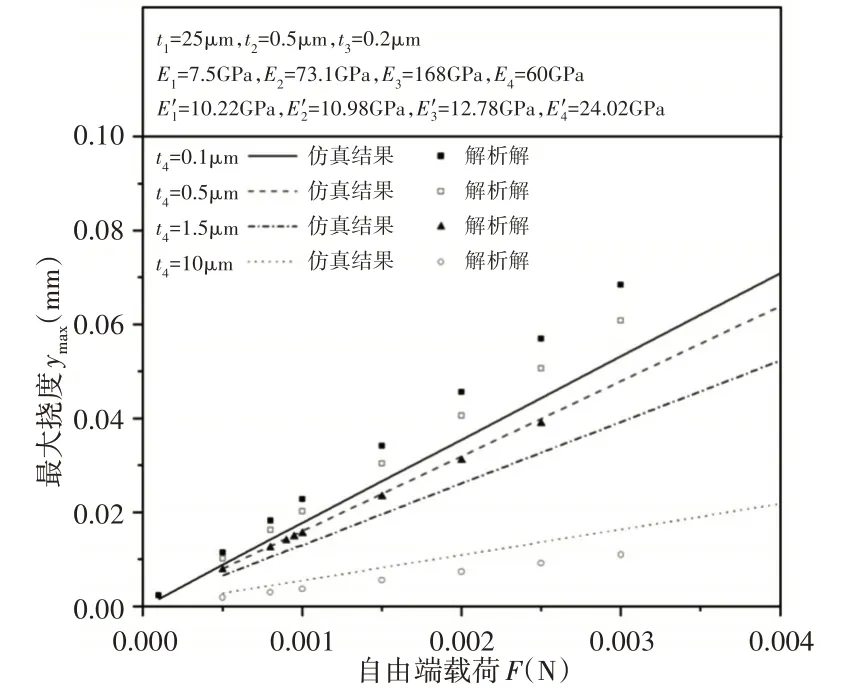
图5 压电多层悬臂梁自由端最大挠度-载荷F曲线Fig.5 Relationship of the Maximum Deflection and Force at the Free End of Piezoelectric Multilayer Cantilever

由图可知，多层膜悬臂梁自由端最大挠度ymax与载荷F呈线性关系，且随着载荷F的增加而增大，表明发生的是线弹性变形。压电层PZT薄膜厚度越大，悬臂梁最大挠度越小。图中仿真结果和理论计算结果虽然有一定的误差，但总体趋势基本一致，验证了有限元仿真模型的可靠性。这种误差可能是由于理论计算采用了平均弹性模量，而对于多层材料平均弹性模量E′的计算目前还没有精确模型来表示。

3.2 曲率半径R与厚度t的关系

为取点方便，在多层悬臂梁的压电薄膜层上从固定端开始沿x方向每隔0.1mm取相应位置的点，如图6所示。分别对应于各点的曲率半径，如图6（a）所示。图6（b）表示了不同压电薄膜层厚度时悬臂梁的曲率半径沿X方向距离的变化曲线，由图可知，悬臂梁的曲率半径在固定端附近较小，越靠近自由端曲率半径越大，挠度也越大，说明曲率半径随着挠度的增大而增大。此外，压电层厚度增大，在同样的载荷条件下，越靠近自由端的曲率半径越小，而靠近固定端曲率半径则越大。

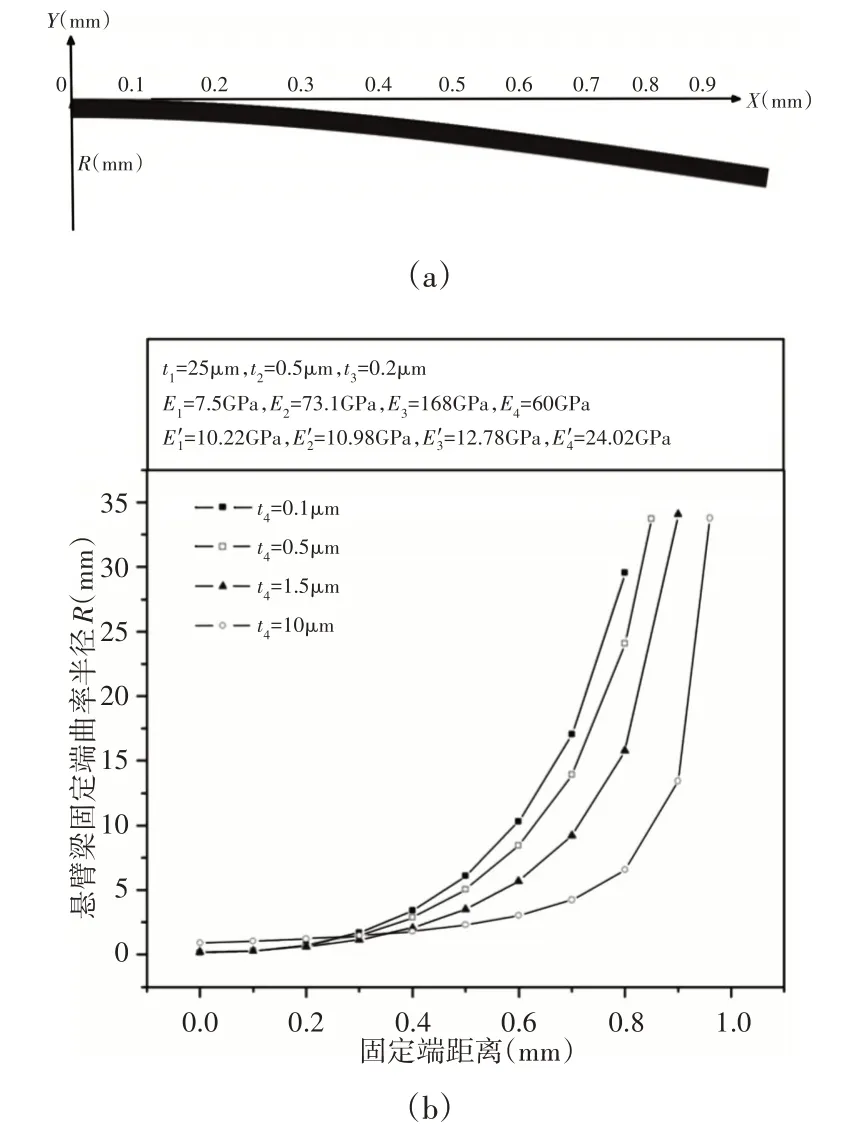
图6 不同压电层厚度的曲率半径与固定端距离的关系Fig.6 Relationship of Curvature Radius and the Distance from the Fxed End for Various PZT Thicknesses

3.3 固定端曲率半径R与压电层厚度t4的关系

悬臂梁压电薄膜层上表面固定端曲率半径与压电层厚度的关系曲线，如图7所示。由图7可知，悬臂梁固定端曲率半径随着压电层厚度的增大而呈线性增加。相同的压电层厚度时，载荷越大，固定端的曲率半径越小。仿真结果与解析结果有一定误差，这是由于悬臂梁仿真结果的曲率半径是在压电层上表面的固定端取点进行计算的，而解析结果的曲率半径是根据悬臂梁总体结构的中性层进行计算的，因此曲率半径的位置不同。此外，解析计算的弹性模量是基于式（4）的计算结果，而仿真计算的弹性模量是根据每层材料的实际弹性模量计算的。尽管结果数值有些差异，但总体趋势是一致的，说明了仿真模型的正确性。

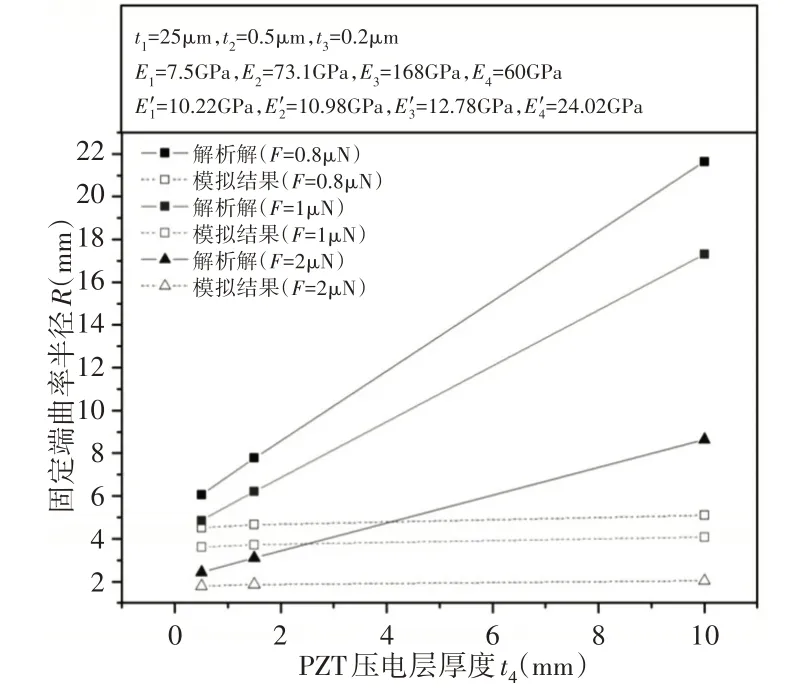
图7 悬臂梁固定端的曲率半径R与压电层厚度的关系Fig.7 Rel ationship of Curvature Radius R at the Fixed End of Cantilever and Various Thicknesses of Piezoelectric Layer

3.4 曲率半径R与应力的关系

压电悬臂梁固定端的等效应力与曲率半径的关系（F=0.5μN），如图8所示。可见，随着压电层厚度的增加，同样的曲率半径条件下，固定端应力减小。同时，固定端等效应力随着曲率半径的增大而减小。曲率半径较小时，应力下降趋势较快，随着曲率半径的逐渐增大，应力下降的趋势变缓。

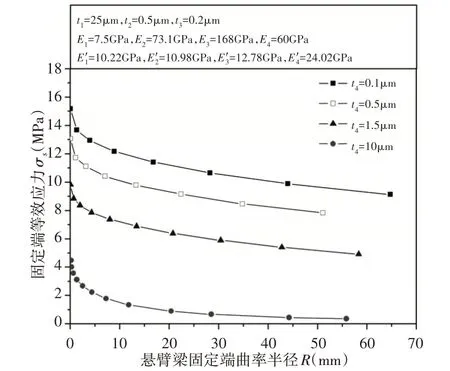
图8 不同压电层厚度时悬臂梁固定端等效应力与曲率半径R的关系曲线（F=0.5μN）Fig.8 Relationship of the Effective Stress and Curvature Radius at the Fixed End of Cantilever for Various Thicknesses under F=0.5μN

4 结论

通过以多层压电微悬臂梁为例，对其自由端受集中载荷时建立了有限元模型，模拟了在基底、过渡层和电极层不变和宽度相同的情况下，不同压电层厚度时悬臂梁的最大挠度与载荷，固定端曲率半径与载荷以及固定端应力与曲率半径的关系。结论如下：（1）讨论了多层悬臂梁的单一弹性模量与等效单层弹性模量对仿真模拟和解析计算结果的影响。结果表明，最大挠度与载荷呈线性关系，且挠度随着载荷的增大而增加，仿真结果与解析计算结果趋势基本一致。（2）曲率半径随着离固定端距离越远和压电层厚度的增大而增大。同样的载荷条件下，压电层厚度越厚，则固定端曲率半径越大，而自由端的曲率半径越小。当压电层厚度t4一定时，载荷F越大，固定端曲率半径R越小。当载荷F≥2μN时，曲率半径R趋近于0。（3）固定端应力随着曲率半径增大而减小，相同曲率半径下，应力随着膜厚的增大而减小。说明增大多层悬臂梁的膜厚对延长MEMS器件的疲劳寿命有着重要意义。将以上仿真结果与解析计算进行比较可知，得到的仿真模拟结果与解析结果吻合较好。以上研究对压电悬臂梁的结构形态设计和性能优化提供了可靠依据。