混合动力客车车身骨架轻量化设计
2021-07-26吴胜军叶欣钰江兴洋
吴胜军,叶欣钰,江兴洋
(湖北汽车工业学院汽车动力传动与电子控制湖北省重点实验室,湖北 十堰 442002)
1 引言
汽车能源和排放是人们关注的焦点,而汽车进行轻量化设计对于节省能源,减少排放,保护环境具有重大意义。近20 年来,国外乘用车每十年减重(8~9)%,商用车减重(10~15)%[1],而我国自主品牌的汽车整备质量则明显高于国外同类型汽车。唐唯伟等将纯电动客车车身骨架作为研究对象,对两种典型工况下车身的强度、刚度及模态进行仿真分析,采用尺寸优化的方法,得到了车身性能更好,质量更轻且结构更加合理的客车模型[2];文献[3]基于四种工况下的有限元分析及全铝车身拓扑优化,对全铝车身结构进行改进,取得的较好的轻量化效果;文献[4]研究了某轻量化车身结构的最优传力路径,同时为了保证车身的正面碰撞安全性,提出了一种合适的形状和尺寸优化处理方法。文献[5]在满足汽车碰撞振动约束条件下,设计研究了一种使用镁合金材料的车身结构,达到了明显减重效果,且相比之前性能更好。文献[6]分析分析了四种典型工况下客车的性能,通过改变客车车架结构,减轻了客车的重量,同时有效的改善了四种工况下的应力和变形情况。
在考虑客车刚度和模态频率合理的情况下,以对客车刚度和模态性能不敏感,对质量敏感的构件的厚度为设计变量,建立质量、刚度、第一阶扭转振动固有频率的响应面模型,并进行多目标尺寸优化,完成对模型的轻量化。
2 混合动力客车初始性能
所研究的混合动力客车车身结构为半承载式,车架为三段式结构。车身上骨架所用材料为Q235 结构钢,地板与车架为Q345钢,其力学属性,如表1所示。车身骨架共2.428t。客车有限元模型,如图1所示。

表1 材料属性Tab.1 Material Properties

图1 客车有限元模型Fig.1 Finite Element Model of HEV
2.1 混合动力客车刚度分析
2.1.1 弯曲刚度
计算车身弯曲刚度时,可以把车身简化成简支梁结构形式,约束前轴与车架连接点XYZ方向自由度,约束后轴与车架连接位置YZ方向自由度,在前后车桥的中点处施加一个垂直向下的力,使车身发生纯弯曲变形,简化模型,如图2所示。

图2 弯曲刚度计算简化示意图Fig.2 Simplified Schematic Diagram of Bending Dtiffness Calculation
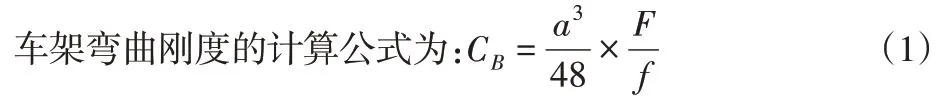
式中:CB—弯曲刚度(N·m2);ɑ—前后轴距离,为5.6m;F—施加载荷大小,为5000N;f—载荷作用点的挠度值为1.854×10-3m,通过计算得到弯曲刚度为9.87×106N·m2。
2.1.2 扭转刚度
由于所研究的是客车右前轮抬起时的情况,所以约束左前轮YZ方向的平动自由度、左后轮XYZ平动自由度和右后轮XZ自由度,并在右前轮处施加一沿Z向相反的作用力,使车身发生扭转变形。简化模型,如图3所示。
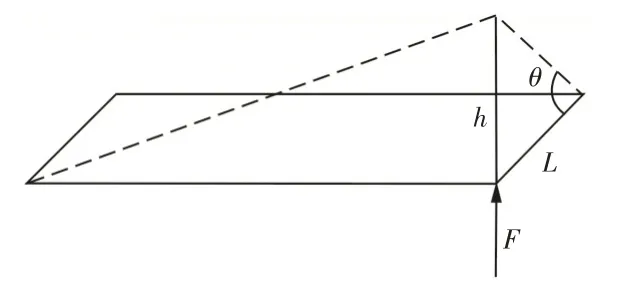
图3 扭转刚度计算简化示意图Fig.3 Simplified Schematic Diagram of Torsional Stiffness Calculation
扭转刚度的计算公式如下:

式中:Cr—扭转刚度(N·m2);L—力臂,为0.695m;F—施加载荷大小,为2000N;h—载荷作用点的挠度值,为0.65mm。受力点最大位移为0.65×10-3m,通过计算得到扭转刚度为2.59×104N·m/(°)。
由于客车的弯曲刚度范围为(2.2×106~4.25×107)N·m2,扭转刚度的范围为(4.5×103~4.11×105)N·m/(°)[7],所以该客车的弯曲刚度和扭转刚度均能够满足车身性能要求。
2.2 客车车身骨架模态分析
对客车而言,高阶振动的主要形式为局部振动,对整车影响较小[8],所以此次的自由模态分析主要研究低阶模态。通过仿真计算得到客车车身骨架前6阶的模态频率,如表2所示。
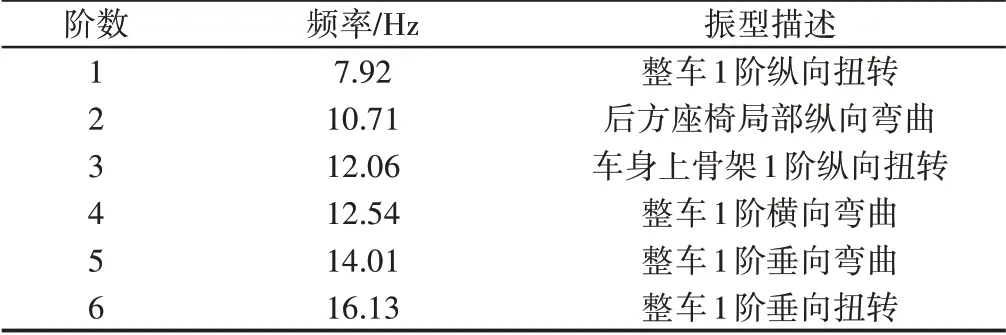
表2 客车车身骨架前6阶模态频率及振型描述Tab.2 The 6th-Order Modal Frequency and Vibration Mode Description of the Bus Body Skeleton
客车在实际路面上行驶时,路面激励和发动机激励为主要激励来源,这些激励可能会造成汽车辆发生共振。对于城市公交而言,路面激励一般在3Hz以下[9],而发动机激励随转速不同而变化,一般在(30~110)Hz之间,从表2可以看出客车前6阶频率为(7.92~16.13)Hz,避免了可能会发生共振的频率区间。
3 车身骨架轻量化
3.1 变量分组
由于客车骨架包含的构件多,所以需要对客车骨架中的构件进行变量分组,从而减少优化计算时间。基于所研究的客车车身骨架包括车身上骨架、车架以及地板等三个部分,所以变量分组依据对称性、所在位置以及厚度进行分组。但由于希望在轻量化的同时不改变客车前端的碰撞性能,所以排除客车前端构件。
将车身上骨架分为2组(S1~S2),车架分为15组(S4~S18),地板分为16组(S19~S33),共33组变量。
3.2 客车车身骨架结构灵敏度分析
通过灵敏度分析可以得到客车车身骨架结构目标响应对各个设计变量的敏感程度,从而进一步得到对车身结构性能不敏感,但对车身质量敏感的构件,对其进行优化,提高优化效率,缩短设计周期。
3.2.1 相对灵敏度理论分析
假设一个系统拥有三个结构性能参数:Tɑ、Tb和Tc,设计变量为xi(xi>0,i=1,2,…,n),建立以下数学模型:
已知:Tɑ和Tb与xi正相关,Tc与xi负相关
要求:min(Tc),Tɑ≤C1,Tb≤C2(C1、C2为常量)
在此数学模型中,设计变量xi的变化会使得结构性能参数的变化趋势不同,为了更加直观有效的获取xi的值,需要分析xi对各个性能指标贡献度的相对大小,即ΔS。
xi对Tɑ的绝对灵敏度为:
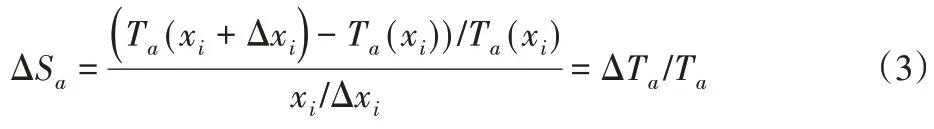
同理可得ΔSb和ΔSc。
ΔSɑc为xi对Tɑ和Tb的相对灵敏度,与ΔSɑ/ΔSc等价,即:
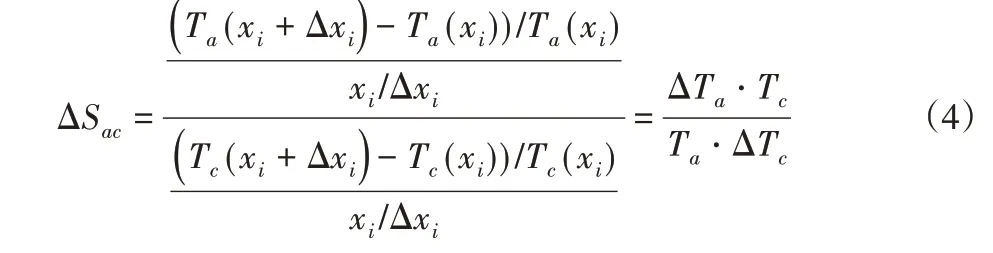
若|ΔSɑc|>1,则说明设计变量xi对Tɑ的影响大于对Tc的响;|ΔSɑc|=1,则说明设计变量xi对Tɑ和Tc的影响等效;|ΔSɑc|<1,则说明设计变量xi对Tɑ的影响小于对Tc的影响;同理可得|ΔSbc|。
3.2.2 相对灵敏度分析
通过上文可得到各个变量弯曲刚度Kb,扭转刚度Kt,一阶扭转频率Ft和质量M的灵敏度。由于量纲不同,各个指标的灵敏度差异很大,没有可比性,所以对其进行量纲化及归一化处理后得到相对灵敏度值,如表3所示。
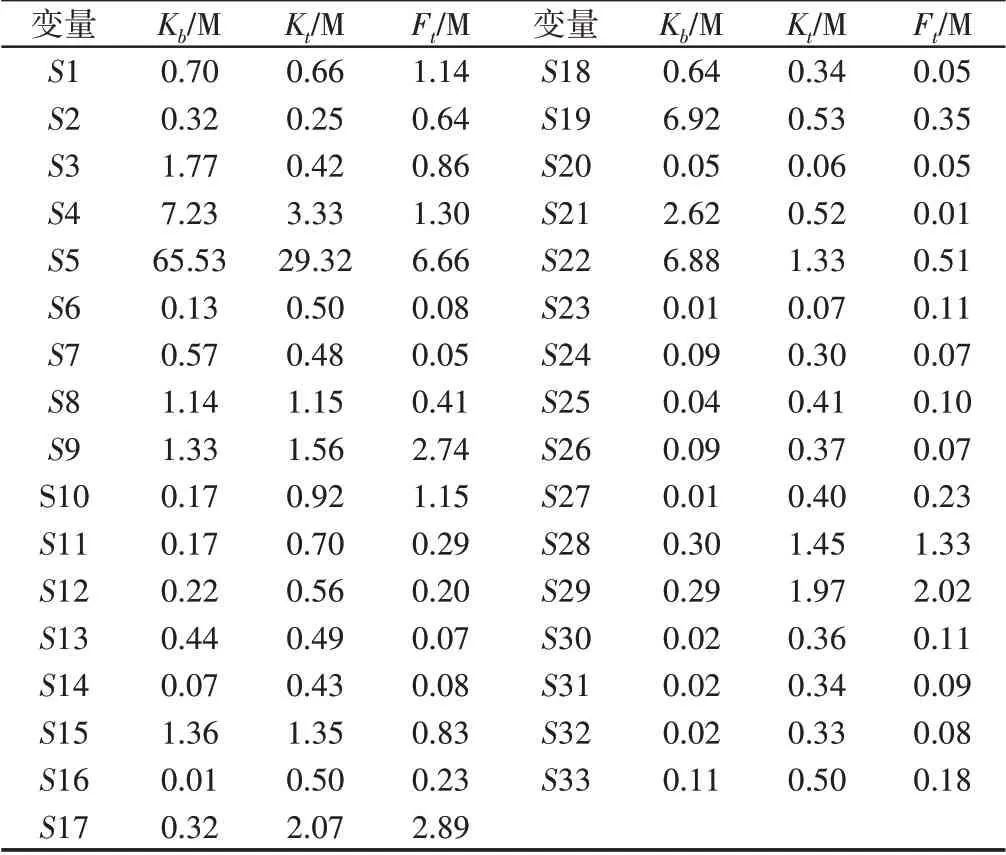
表3 相对灵敏度值Tab.3 Relative Sensitivity Value
根据前文所述,选取相对灵敏度小于1的构件作为最终设计变量。从表3可知,构件S5的各项相对灵敏度都过大,所以可以排除。其余构件的相对灵敏度折线图,如图4所示。从图中可以看出各个响应的相对灵敏度均小于1 的变量为S2、S6、S7、S11、S12、S13、S14、S16、S18、S20、S23、S24、S25、S26、S27、S30、S31、S32、S33。
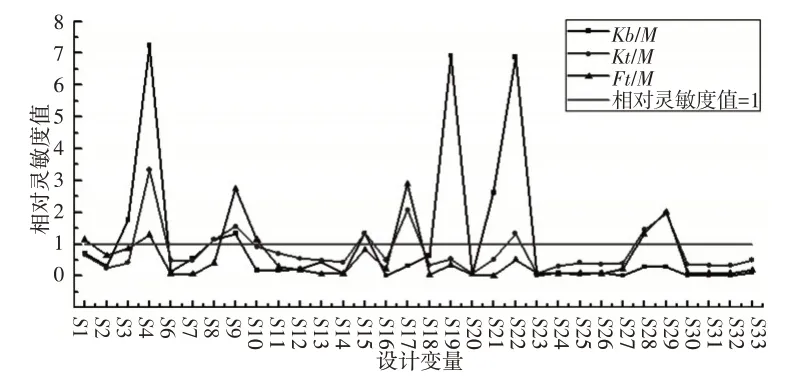
图4 相对灵敏度折线图Fig.4 Relative Sensitivity Line Chart
3.3 多目标优化问题描述
车身性能考核的主要指标为弯曲刚度和扭转刚度,而扭转刚度的大小对汽车底盘的操纵稳定性、行驶在凹凸路面上车体的抗变形能力影响比较大,所以,将扭转刚度作为目标之一。将前文得到的19个变量作为设计变量,以客车车身骨架质量最小、扭转刚度最大为优化目标,同时要求弯曲刚度和一阶扭转频率不小于原来的95%,对客车车身骨架进行多目标优化,多目标优化的数学模型为:

式中:x1,x2,…,x19—19个设计变量;ximin,ximax—第i个设计变量上限值和下限值,这里为设计变量原始值的±50%;M—车身骨架总质量;Kt—客车扭转刚度;Kb—弯曲刚度;K0的原始弯曲刚度;Ft—一阶扭转频率;F0—原始一阶扭转频率。
3.4 优化结果
多目标优化问题的解不是唯一的,而是生成一个最优解的集合,即Pareto 最优解集。通过HyperStudy 软件进行多目标求解,得到多目标优化最优Pareto解集,如图5所示。
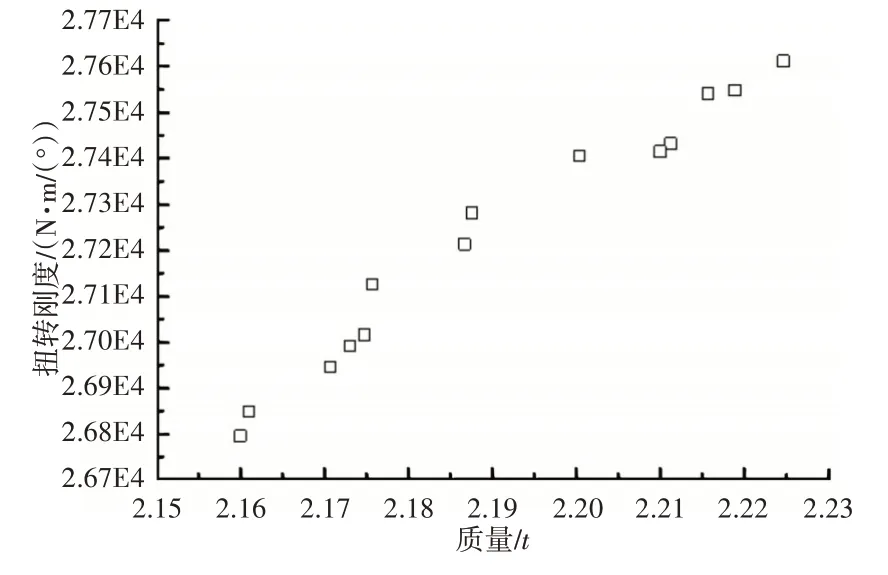
图5 Pareto解集Fig.5 Pareto Solution Set
从图5中可以看出,客车车身骨架的扭转刚度与客车车身骨架的质量,这两个目标响应是相互矛盾的。若想要质量最轻时,必定会使得扭转刚度变小,相反若使扭转刚度大,则会使结构的质量增加。综合考虑车身质量和扭转刚度两个目标选定最终选定优化结果,如表4所示。具体位置,如图6所示。

表4 优化结果Tab.4 Optimization Results
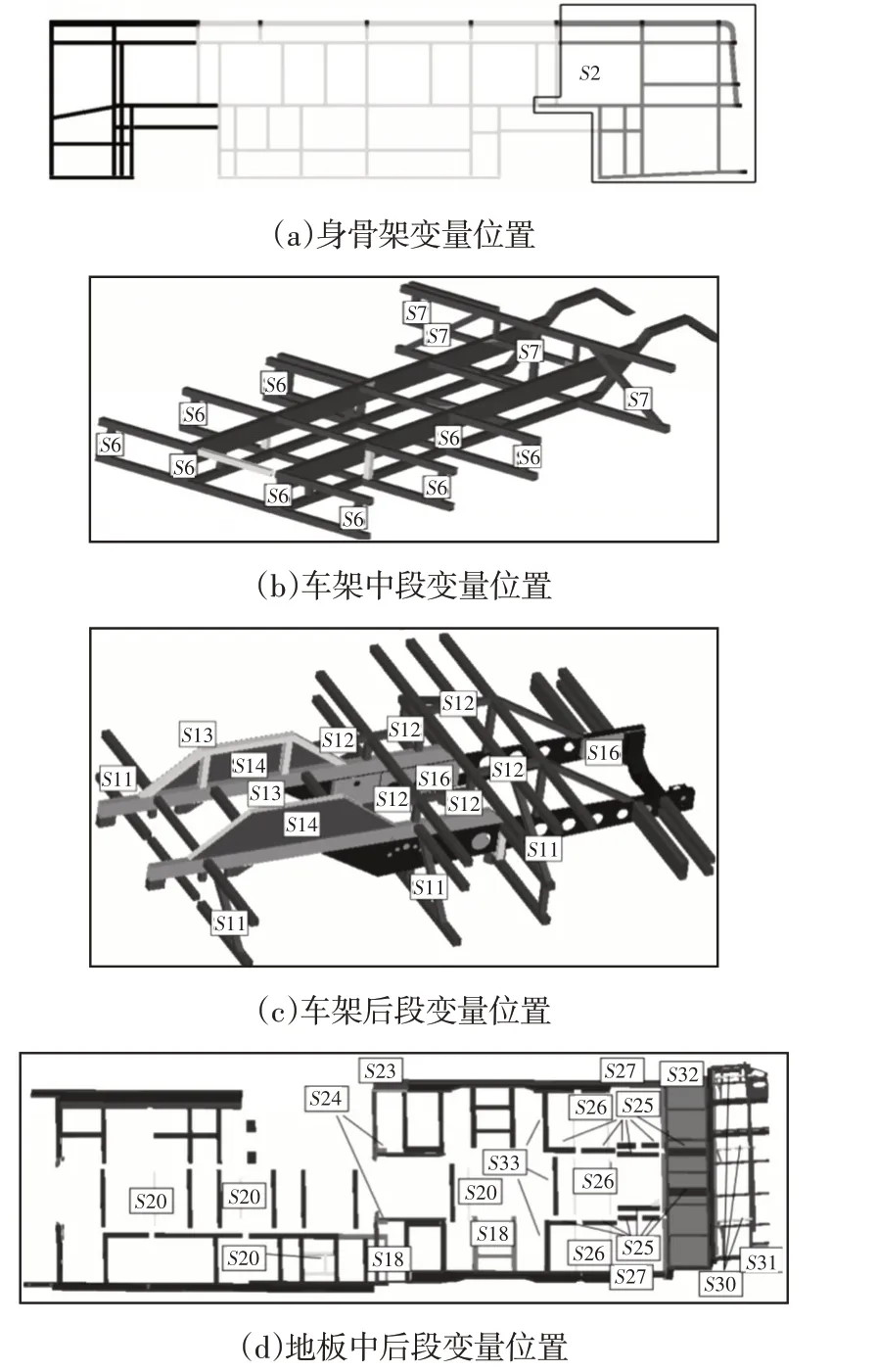
图6 变量位置Fig.6 Variable Position
4 优化前后性能对比
优化后的客车车身骨架质量为2.169t,比原始客车结构减重259kg,轻量化程度达到10.67%,轻量化结果显著。通过对比优化前后模型的性能检验优化方案的合理性及有效性。
将计算得到的优化后模型与优化前模型做对比,具体如表5、表6所示。

表5 优化前后客车骨架刚度对比Tab.5 Stiffness Comparison between Optimization Model and Design Model

表6 优化后客车车身骨架前6阶模态频率Tab.6 First 6 Modal Frequency Comparison Between Optimization Model and Design Model
从表5中可以看出,弯曲刚度和扭转刚度均有所增加,且满足客车刚度范围。从表6中可以看出,优化后客车车身骨架低阶模态频率普遍降低,频率范围(7.86~15.36)Hz之间,避开了路面激励和发动机激励。认为优化是符合设计要求的。
5 结论
研究以混合动力客车骨架构件厚度为设计变量,以质量最小、扭转刚度最大为优化目标,以弯曲刚度和一阶扭转频率不小于原来的95%为约束条件的多目标优化。优化后的客车减重259kg,弯曲刚度和扭转刚度较原始模型有所提高,低阶自由模态避开了路面激振频率以及发动机激励,说明优化方案合理。
