船拖分动箱齿轮啮合特性分析

周明刚，王 俊，龚 宇，刘明勇

（1.湖北工业大学农机工程研究设计院，湖北 武汉 430068；2.湖北省农业机械工程研究设计院，湖北 武汉 430068）

1 引言

船式拖拉机工作环境主要为深泥脚水田，该环境下普通拖拉机工作过程中易出现下陷，内在动力不足等现象，导致不易耕种，效率低。基于“浮式”原理的船式拖拉机利用船体接地比压大的特点，很好克服普通拖拉机在水田作业时的各种缺点。船式拖拉机由船体和驱动轮承担整机的重量和工作中提供大马力，水田作业时受到泥浆、水坑、作物等外部激励，引起整机振动，加剧关键零部件的损坏。因此，研究分动箱系统的特性对提高工作效率和使用寿命具有重要的指导意义。

在对齿轮研究中，文献[1]利用有限元法建立弧齿锥齿轮模型进行接触仿真分析，分析出齿轮啮合过程齿面接触区压力分布情况。文献[2]考虑此轮加工误差、装配误差和修形等因素，计算齿轮的接触应力和弯曲应力。文献[3]通过编程软件分析不同安装情况下轮齿的接触轨迹及传动误差影响。文献[4]建立孤齿线锥形齿轮齿轮副的齿面接触模型，得到双刀盘半径对齿轮副接触椭圆大小和安装误差影响。文献[5]分析船用交错变厚齿轮传动啮合特性，得到中心距误差、传动误差对啮合印痕、最大接触压力及啮合刚度影响规律。文献[6]建立新型传动形式有限元接触模型，得到齿面接触等效应力和实际啮合齿对数，分析其承载能力。文献[7]采用I-DEAS，对重载齿轮传动系统中渐开线斜齿轮的弹性变形进行有限元分析计算。文献[8]利用有限元法分析出斜齿轮静态和动态过程接触应力，分析数据得出齿侧间隙对接触应力影响。文献[9]利用有限元法分析齿轮齿根的弯曲应力，为齿轮性能分析提供参考依据。文献[10]考虑齿轮弯曲变形、剪切变形、压缩变形和赫兹接触变形，计算齿轮啮合刚度。文献[11]建立齿轮啮合接触冲击模型，分析不同转速、冲击位置对冲击合力和冲击应力的影响，并利用解析分析计算式验证仿真结果的可靠性。文献[12]以渐开线圆柱齿轮副为研究对象，计算齿轮各个方向的应力分布，得到啮合过程中齿根弯曲应力的变化情况。文献[13]建立多齿轮轴三维模型，考虑法向载荷和偏差量对齿轮齿面啮合力的影响。文献[14]建立多级齿轮副的运动微分方程，分析齿轮传动在稳态运动过程中齿面啮合力、啮合变形。上述学者们研究某些因素对齿轮啮合过程接触应力、弹性变形影响，提供优化设计齿轮的理论依据和齿轮啮合刚度计算方法。对分析齿轮啮合特性具有极其重要的意义。

因此，在齿轮啮合原理、摩擦学、接触力学理论研究基础下，以船式拖拉机分动箱齿轮为研究对象，基于有限元分析软件，进行齿轮啮合过程的仿真分析。对分析结果进行后处理，分析热弹耦合和在不同摩擦系数接触下齿轮啮合过程齿面所受力、接触应力、和时变啮合刚度变化规律，为后续计算齿轮啮合过程中产生的内部激励，进行分动箱系统动态响应分析作基础。

2 船式拖拉机传动系统

由于工况十分复杂、工作环境恶劣和确保整机具有多功能，新型船式拖拉机选用4L88型柴油发动机，提供大马力动力保证能高效的完成耕种作业。船式拖拉机动力传递系统简图，如图1所示。发动机动力通过离合器传给变速箱输入轴，经过变速箱变速动力由变速箱输出轴传给分动箱输入轴，动力经过分动箱齿轮分配给前桥和后桥和增大扭矩来驱动驱动轮。普通拖拉机和机耕船靠后轮驱动，在水田作业过程中会存在深陷、动力不足等现象。该船式拖拉机分动箱将发动机的动力传递给前桥和后桥，增大扭矩并很好克服了普通拖拉机工作时的各种缺点，因此分动箱传动系统特性研究有着重要的意义。

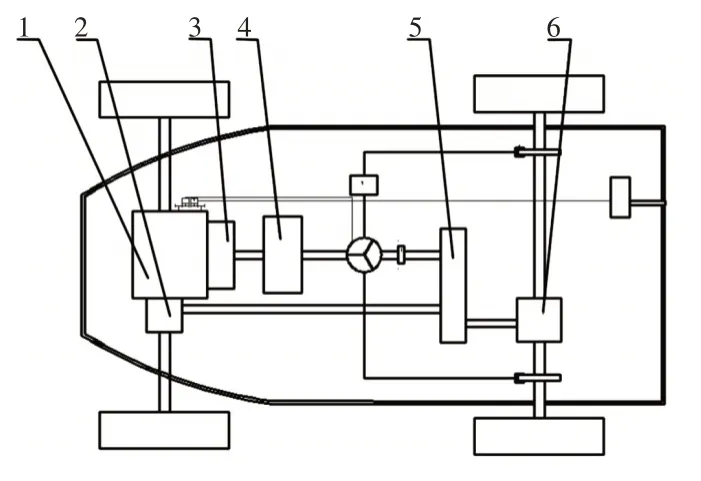
图1 船式拖拉机传动系统简图Fig.1 Schematic Diagram of Ship Tractor Transmission System

3 分动箱直齿圆柱有限元建模

采用理论分析与有限元分析相结合的方法，建立基于船式拖拉机分动箱齿轮传动系统有限元模型，以分动箱一级传动的齿轮对为研究对象，齿轮的基本参数，如表1 所示。在SolidWorks中进行齿轮的建模与装配，因齿轮在啮合过程主要考虑轮齿齿面的接触应力与齿根的弯曲应力，故可对齿轮进行简化处理，提高计算精度和减少计算时间，如可适当增加轮毂半径。

表1 齿轮基本参数Tab.1 Basic Gear Parameters

根据两个齿轮中心距确定齿轮安装位置，装配过程中需要适当的调整轮齿的位置，确保该装配体没有发生干涉。为了提高仿真精度和数据的可靠性，瞬态仿真过程中参与啮合的几对轮齿表面网格细化，减小仿真误差。齿轮模型，如图2所示。齿面网格细化模型，如图3所示。

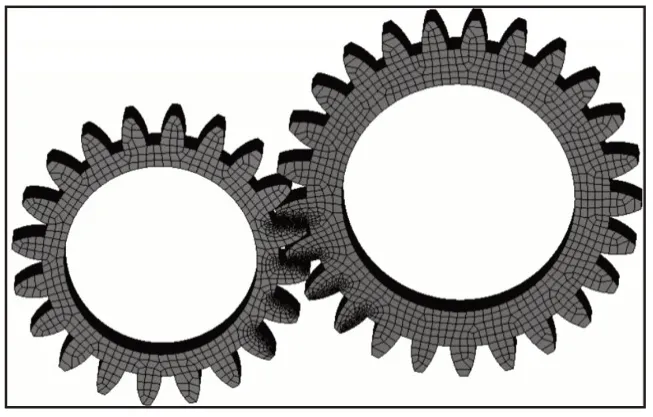
图2 有限元网格划分Fig.2 Finite Element Mesh Generation

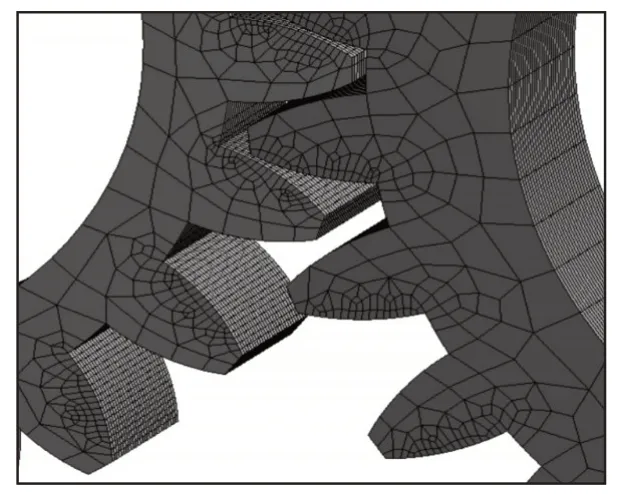
图3 齿轮啮合区网格细化图Fig.3 Mesh Refinement Diagram of Gear Mesh Area

3.1 约束与载荷

有限元分析前处理主要包括定义材料属性、设置接触方式、划分网格、设定施加载荷和约束边界条件。齿轮啮合仿真过程中存在很多因素对仿真结果的影响，如装配位置不同导致分析过程齿轮啮合位置的不同、网格质量等。ANSYS中赋予材料参数：弹性模量E为206GPa，泊松比μ为0.3，密度ρ为7850kg/m3。齿轮啮合分析主要对齿轮弹塑性变形、应力应变、大变形等特性。在设置的仿真时间内，啮合的几对轮齿齿面选用对称性的无摩擦接触方式，采用罚函数计算方法进行仿真。采用六面体与四面体混合网格划分方法进行有限元模型网格划分，并在分析时间段内啮合的几对齿轮接触齿面进行细化处理。已知发动机的额定功率和转速和变速箱的传动比，故载荷的施加方式为主动轮施加角速度20rad/s，从动轮施加转矩2.5e6N·mm。根据齿轮的运动特性将齿轮的内表面约束x、y轴四个自由度和z轴移动自由度，确保齿轮只能绕z轴转动。齿轮瞬态分析约束与载荷施加情况，如图3所示。

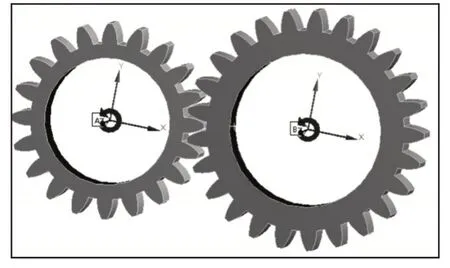
图4 齿轮啮合施加载荷情况Fig.4 Load Applied by Meshing of Gears

3.2 热弹耦合模型建立

齿轮啮合过程中，啮合齿面摩擦生热和齿轮与润滑油强制对流换热使得齿轮最终保持热平衡状态。齿面摩擦产生热量一部分通过热传动传递齿轮，另一部分通过润滑油强制对流冷却。有限元进行齿轮轮齿温度分析，需要准确确定齿面热流通量和齿轮对流换热系数。齿轮摩擦热流通量主要受到齿轮啮合时相对滑动速度、啮合面接触压力和啮合面摩擦系数的影响。主从动轮齿面摩擦热流通量q1和q2公式为：

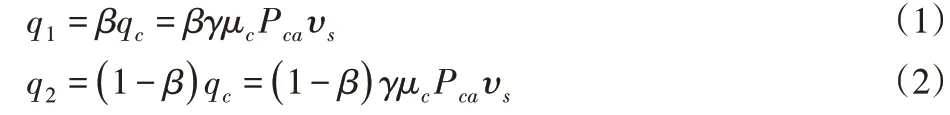
齿轮端面对流换热系数公式进行确定：

当Re≤2×105，齿轮端面对流换热系数为：

齿顶面、齿根面的对流换热系数简化取齿轮啮合面对流换热系数的1/3。在上述模型基础上施加对流换热系数、热流通量，重复上述过程。

4 仿真结果分析

选用Ansys/workbench 瞬态动力学模块对直齿轮啮合过程进行仿真分析，对仿真结果进行必要的后处理。由于直齿轮的重合度一般在（1～2）之间，因此齿轮啮合过程中即是单齿对接触与两齿对接触交替出现形式。选取输入级主动齿轮，根据旋转时间的不同，得到齿轮单个轮齿从啮入、啮出这一过程的具体变化情况，如图5所示。2齿啮入，1齿从单齿啮合转化为双齿啮合，如图5（a）所示；1齿退出啮合，2齿为单齿啮合，如图5（b）所示；4齿啮入，2齿从单齿啮合变成双齿啮合，如图5（c）所示。

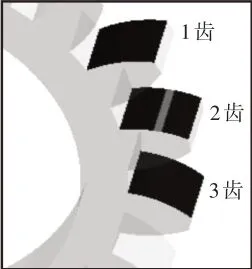
图5 主动轮啮合变化过程Fig.5 Driving Wheel Engagement Change Process

上图清楚的反映齿轮啮合过程，得出随着时间的变化齿面载荷从齿根逐渐向齿顶移动，再者由于齿轮啮合过程中单、双齿啮合交替的出现，使得原本由两对轮齿承载的法向载荷，突然全部由一对轮齿承载，或者原本由一对轮齿承载的法向载荷，突然由两对轮齿承载，从而作用在轮齿上的载荷随着啮合位置的不同会发生突变。根据定义角速度载荷，随着时间的变化，依次提取一齿面从啮入到啮出整个过程中，不同时刻单个轮齿接触节点的法向载荷之和与轮齿接触部位节点接触平均压力之和，拟合出输入级主动齿轮单个齿面接触力变化曲线，如图6所示。接触压力变化曲线，如图7所示。由图6、图7说明在单、双齿交替位置处，齿面受到的接触力与接触压力会发生突变，在双啮合区其所受载荷与接触压力较平稳，其区域齿轮受到冲击较小。

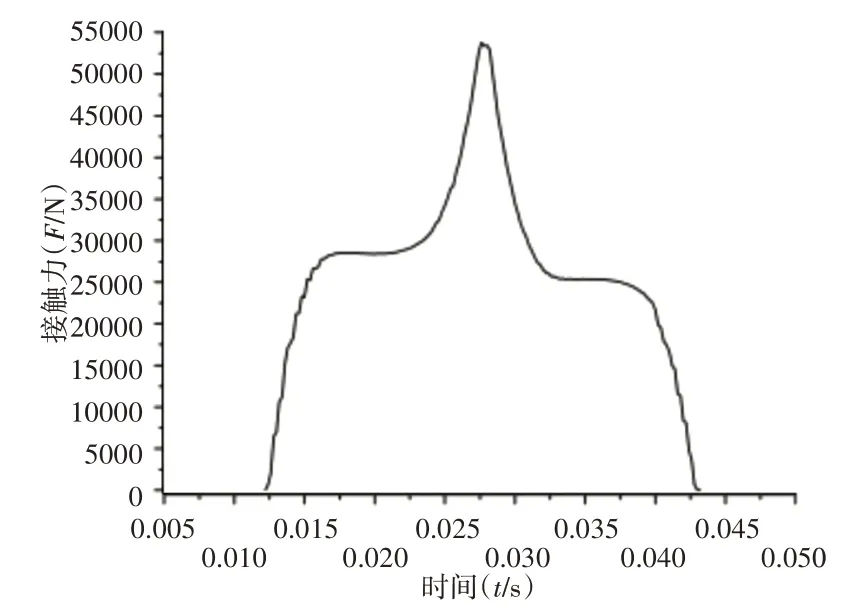
图6 主动齿轮单齿对接触力变化Fig.6 Change of Contact Force of Single Tooth of Driving Gear

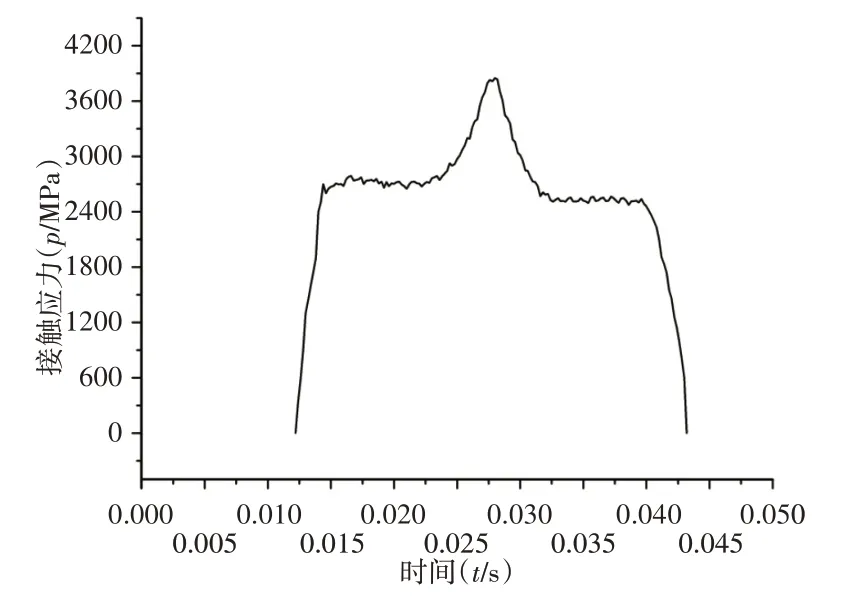
图7 主动齿轮单齿对接触压力变化Fig.7 Change of Contact Pressure of Single Tooth of Driving Gear

啮合轮齿齿面法向变形量主要考虑下列两种变形：相互接触轮齿接触区域由所受载荷引起的接触变形；参与啮合轮齿发生弯曲变形引起的接触节点的变形。提取出不同时刻所接触节点发生总变形量减去该接触节点该时刻转动的弧长即得到该时刻接触节点所发生的综合变形。以一个轮齿为研究对象，根据前面得到的齿面接触力与轮齿接触区域发生的综合变形，根据公式可得单齿对啮合刚度，其结果，如图8所示。将同时啮合的几对轮齿的单对齿啮合刚度进行叠加，即得到轮齿时变啮合刚度，主动轮时变啮合刚度曲线，如图9 所示。因齿轮啮合过程单齿对接触，载荷全部由单齿承载，其接触区域对应的综合变形量较大，使单齿对接触时时变啮合刚度值较小；双齿对接触时，其接触区域对应综合变形较小，使齿轮时变啮合刚度增大。双齿啮合区最大时变啮合刚度值为57.04155N/mm/μm，单齿啮合区最大时变啮合刚度值为29.56N/mm/μm。

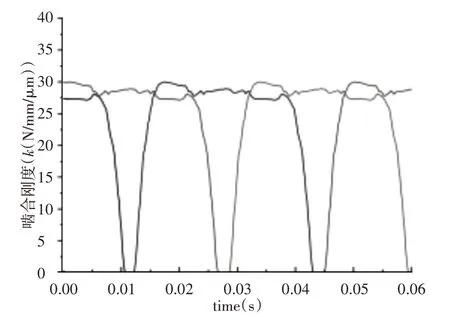
图8 齿轮多个单齿啮合刚度曲线Fig.8 Meshing Stiffness Curves of Multiple Single Teeth of Gears

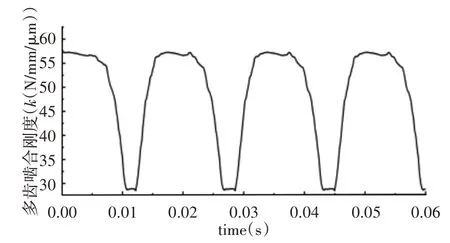
图9 主动齿轮时变啮合刚度曲线Fig.9 The Time-Varying Meshing Stiffness Curve of the Driving Gear

4.1 仿真值与石川公式对比

根据不同的齿轮模型，齿轮啮合刚度数值算法有所不同。采用石川公式计算直齿轮啮合刚度，石川法是基于材料力学计算轮齿变形的计算方法，在轮齿变形理论计算中常见的计算方法。计算齿轮啮合刚度时需要对齿轮轮齿进行适当的简化，石川公式即将轮齿分为矩形和等腰梯形两个部分，如图10所示。

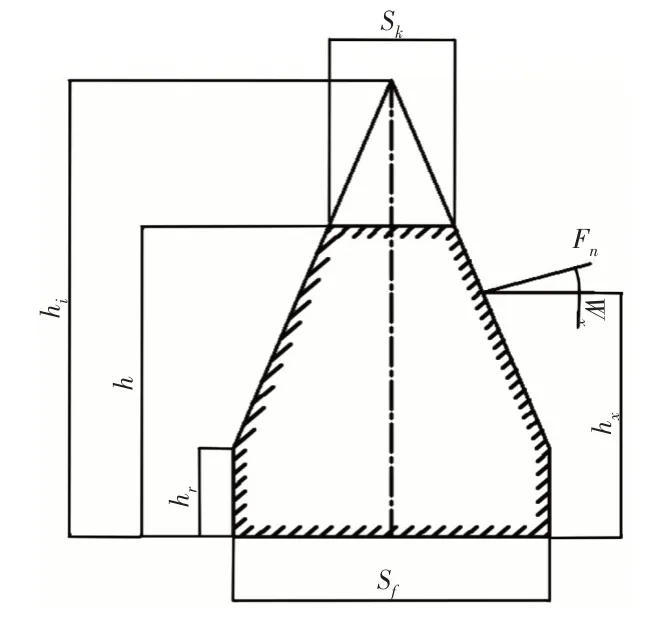
图10 石川公式简化轮齿模型Fig.10 Ishikawa Formula Simplified Gear Tooth Model

单个轮齿齿面啮合过程中受到法向载荷沿啮合线方向产生的变形量δ计算公式为：

式中：z—齿数；x—变位系数；rg—基圆半径；rk—齿顶圆半径；rr—齿根圆半径；rF—有效齿根圆半径；rx—载荷作用点到齿轮中心点的距离；α0—压力角；αx—啮合角。

一对齿轮啮合时，参与啮合的各个齿轮轮齿齿面在法向载荷作用下沿啮合线方向总的变形量δΣ为：

式中：δ1、δ2—相啮合的两个轮齿的变形量；δpv—啮合的轮齿齿面接触区域的变形量。

轮齿的刚度表示为单位齿宽上产生1μm的齿面法向变形量所需法向载荷，其计算公式如下：

根据以上公式，通过计算机编程即可得到齿轮啮合过程中的时变啮合刚度。仿真值与理论计算值对比情况，如图11所示。齿轮最大时变啮合刚度仿真值比理论计算值大5.6325%。验证了有限元分析齿轮啮合特性方法和建立有限元模型的可行性。

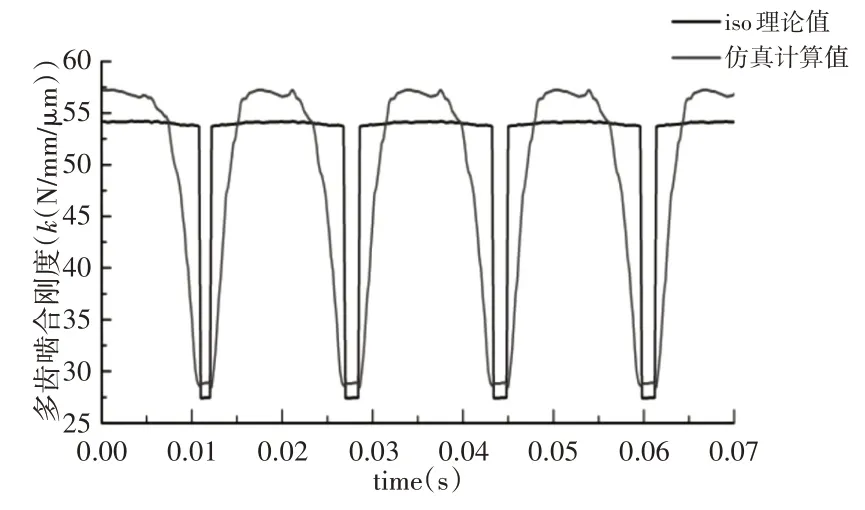
图11 齿轮时变啮合刚度曲线Fig.11 Time-Varying Meshing Stiffness Curve of Gears

4.2 基于热弹耦合仿真分析

瞬态分析过程中，参与啮合的几对齿面施加热流通量，齿顶面、齿根面、齿轮端面分别施加对流换热系数。边界条件、材料特性、接触方式设置不变，重复上述仿真过程。轮齿温度场，如图12所示。

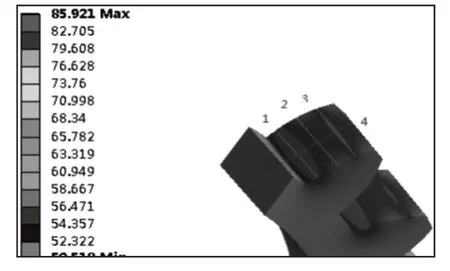
图12 主动齿轮齿面温度场Fig.12 Driving Gear Tooth Surface Temperature Field

图12为齿轮啮合过程中输入级主动轮啮合面与非啮合面温度场分布情况，分别在齿高、齿宽方向提取4条路线温度变化曲线。由图可知，齿轮啮合面温度比非啮合面温度高，且啮合面呈现两个温度峰值区，因在单齿啮合和双齿啮合交替出，相对滑动速度大，而摩擦产生的热流通量和相对滑动滑动速度成正相关，故单双齿啮合交替时刻热流通量增加，所以齿轮轮齿啮合面会出现两个局部温度峰值区。

路线1、2、3、4可知，沿齿宽方向温度场分布呈现向上抛物线形式，其中间温度高（最高温度为85.3℃），两边端面温度低，因齿轮端面与尤其混合物对流散热所致，如图13、图14所示。路线4温度分布情况得到齿面最小温度区域位于齿顶修型处，因齿顶修型改变了该处摩擦产生热流通量的分布和齿顶与外部环境对流换热，降低了齿顶温度场。

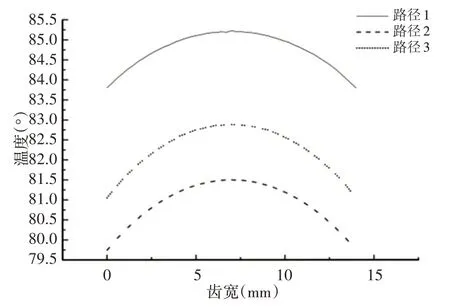
图13 齿轮轮齿齿宽温度变化情况Fig.13 Change of Tooth Width and Temperature of Gear Wheel

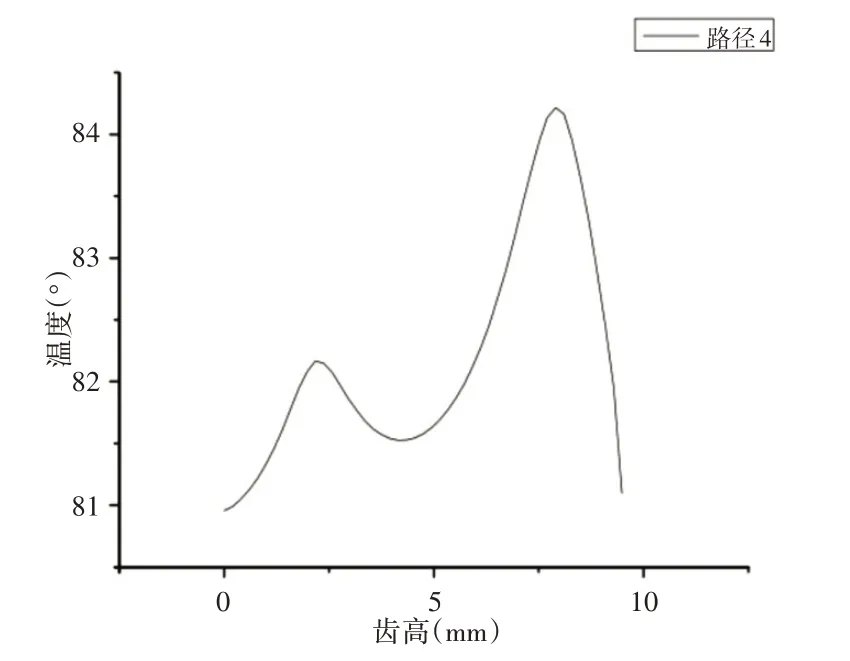
图14 主动齿轮齿顶到齿高温度变化情况Fig.14 Change in Temperature From Tooth Tip of Driving Gear to Tooth Height

基于热弹耦合齿轮啮合时单齿面接触压力小于不考虑温度场齿面接触压力，因摩擦生热导致齿面膨胀，啮合过程中齿面接触面积增大，导致齿面接触应力变小，如图15所示。考虑温度场单齿啮合刚度比齿轮啮合过程不考虑温度场啮合刚度值小，如图16所示。主要因为齿轮啮合刚度是指单位齿宽产生1μm变形所需要的力，而考虑温度场齿轮啮合过程齿轮轮齿产生的总变形变大，根据k=Fn/δB，所以齿轮啮合刚度变小。

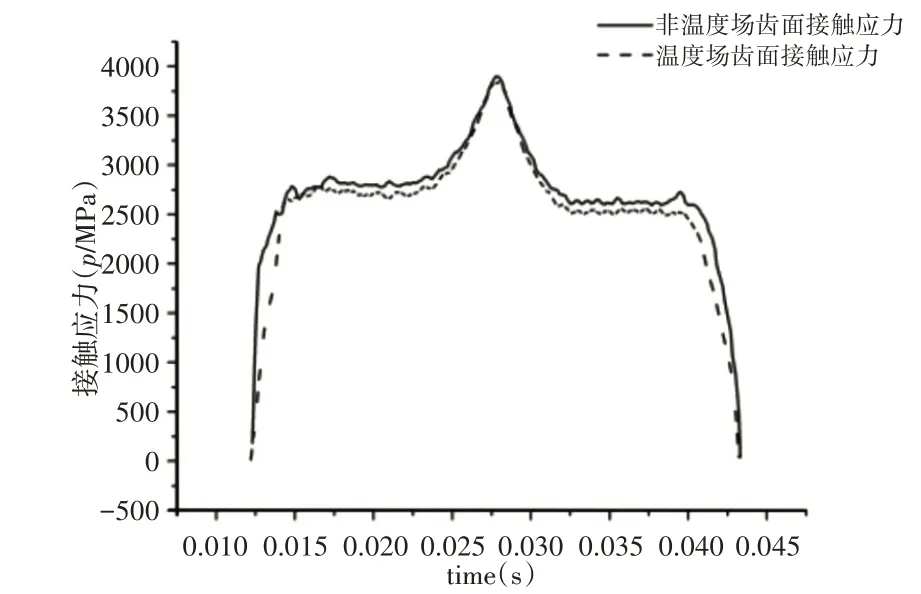
图15 考虑温度场齿面接触压力Fig.15 Consider the Temperature Field Tooth Surface Contact Pressure

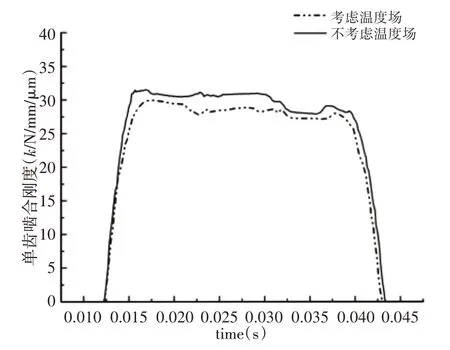
图16 考度温度单齿啮合刚度Fig.16 Test the Meshing Stiffness of Single Tooth with Temperature

4.3 不同摩擦系数对啮合特性影响

有限元仿真过程，将齿面无摩擦接触改为摩擦系数分别为0.05，0.06接触方式，即得到摩擦系数对齿面接触压力影响，如图17所示。

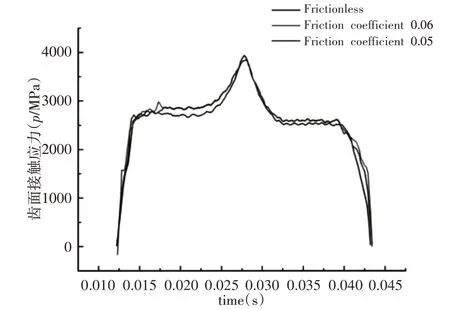
图17 不同摩擦系数对齿面接触压力影响Fig.17 Influence of Friction Coefficient on Contact Pressure of Tooth Surface

因齿轮啮合过程单齿啮合是轮齿间摩擦状态为滑动摩擦，双齿啮合时齿面间摩擦由滑动摩擦变为静摩擦，滑动摩擦区间轮齿接触面积较小，故考虑摩擦系数齿面接触应力大于不考虑摩擦系数齿面接触应力。摩擦系数对齿轮单齿啮合刚度影响，如图18所示。主动轮轮齿啮入双啮合区到单齿啮合区摩擦接触时齿轮单齿啮合刚度大于无摩擦接触单齿啮合刚度，单啮合区到啮出过程摩擦接触时齿轮单齿啮合刚度小于无摩擦接触单齿啮合刚度。

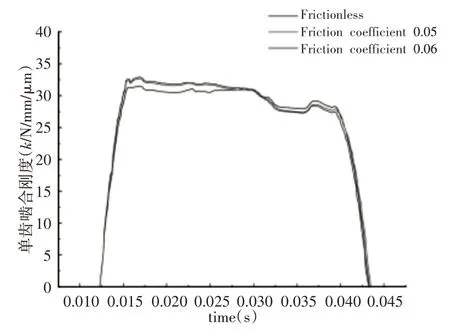
图18 不同摩擦系数对单齿啮合刚度影响Fig.18 The Influence of Different Friction Coefficients on the Meshing Stiffness of Single Teeth

5 总结

（1）双啮合区，齿轮齿面受到的法向载荷和接触压力较平稳；双、单齿交替啮合处，其受到的法向载荷和接触压力发生突变，其实产生啮合冲击激励的主要来源。

（2）有限元仿真分析得到齿轮综合啮合刚度比石川公式计算得到的齿轮综合啮合刚度大5.6325%，验证该齿轮模型的可行性和仿真分析数据的可靠性。

（3）双齿啮合区齿轮时变啮合刚度比单齿啮合区齿轮时变啮合刚度大，因单齿啮合时输入载荷由单个轮齿承载，齿轮接触区域产生综合变形较大。由此可得单齿啮合对齿轮传动系统磨损较大，即可考虑设计合理齿形以此来增大单齿啮合时齿面接触面积，减小接触区的综合变形，提高齿轮啮合刚度。

（4）摩擦生热、摩擦系数对齿轮啮合特性有一定影响。需要精确考虑齿轮啮合特性时，该因素应作为关键因素分析。