改进人工蜂群优化神经网络的短期负荷预测

马松龄，代一楠，徐军昶，马 健

（1.西安建筑科技大学机电学院，陕西 西安 710055；2.陕西省西安市气象局，陕西 西安 710016；3.陕西省西安市供电公司，陕西 西安 710089）

1 引言

电力系统短期负荷预测是根据历史负荷变化规律，结合气象、社会活动等因素对未来几天或几小时负荷进行的科学预测[1-3]。高效、准确的负荷预测对各经济实体的利益得以保证，其中保证输配电企业里各条线路输送的容量安全性与经济性；减少发电企业中发电机组备用容量以避免未能满发或者效益过低，有助于应对紧急情况。因此，提高负荷预测精度和预测速度是迫切需要解决的问题。

传统短期负荷预测主要采用时间序列法、线性分析法等[4]，其缺点是仅仅依据电网数据，对环境、社会等影响因素考虑不足。近年来，为提高预测精度，对温度、生产情况、社会生活环境等影响越来越多纳入考虑，这样海量数据情况下，使用结构简单的BP神经网络建模最为适宜。但BP神经网络预测方法的不足是神经网络的初始值较敏感，大多依据主观经验确定，导致预测速度不理想且误差较大。为解决上述问题，提出一种改进人工蜂群算法优化BP神经网络的预测方法。首先，利用高斯滤波将负荷数据和湿度、温度等天气数据融合进行预处理，再采用人工蜂群算法搜索位置更新方案的改进，得到最佳的网络参数；最后建立改进后预测模型。通过Matlab 平台完成实例仿真实验，结果表明IABC-BP优化模型平均绝对百分误差为1.353%且收敛速度大幅提高，从而验证了预测模型的精准性与可靠性。

2 人工蜂群算法及其改进

2.1 人工蜂群算法

人工蜂群算法（Artificial Bee Colony，ABC）是一种模拟蜂群寻找蜜源过程的群体智能优化算法，具有结构简单、调节参数较少以及易于实现等特点[5]。算法定义的人工蜂群分为三种：雇佣蜂、跟随蜂和侦察蜂[6]。三种蜜蜂通过分工协作实现蜜源的开采，并通过对蜜源的标记与分享不断更新位置寻找到最优蜜源。其中，蜜源的位置对应优化问题的可行解，而蜜源的质量以优化问题的适应度值来衡量。在搜索过程中雇佣蜂和跟随蜂的蜜源位置更新公式为：

式中：r—［-1，1］之间的随机数，控制Sij邻域内的生成范围；k∈（1，2，…，L），j∈（1，2，…，N），k≠j；Sij—当前蜜源的位置；Skj—一个领域内随机选择蜜源的位置。

雇佣蜂完成搜索后通过标记与跟随蜂分享蜜源信息，随后跟随蜂采用轮盘赌方式对蜜源进行选择，其概率为：

式中：δi—第i个蜜源；f（δi）—第δi个蜜源的适应度值，i∈（1，2，…，T）；T—蜜源的数量。该蜜源对应的概率越大，被选择的机率越大。

2.2 人工蜂群算法的改进

随着电力系统数据量的增加，利用人工蜂群算法建模时不难发现：由于雇佣蜂与跟随蜂都是按照所寻找蜜源的邻域内进行寻优，其搜索的范围存在一定的局限性。为改善人工蜂群的性能，现有文献中有学者参考粒子更新的思想对其进行改进[7]，即在进行搜索时引入了全局最优解这一参数来提高预测精度并加快收敛速度，其蜜源搜索的位置更新公式为：

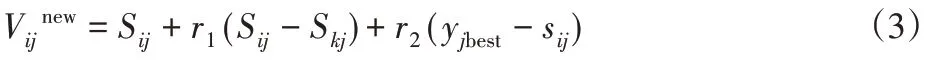
式中：r1—（0，1）之间的随机数；r2—（0，1.5）之间的随机数；yjbest—种群最优蜜源的第j个变量。

但此方法的实际搜索过程是非线性且高度复杂的，往往不能反映实际的优化搜索过程，并且会出现收敛到局部极值点的现象，导致此时搜索的寻优性能提升不明显。为达到收敛速度与种群多样性的动态平衡，在引入全局最优解的同时加入了自适应的惯性因子ω1与ω2，得到了改进的人工蜂群算法：

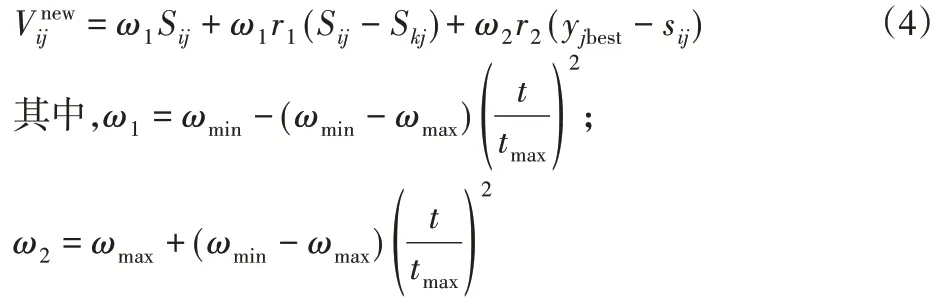
式中：t、tmax—当前迭代次数与最大迭代次数；ωmax、ωmin—惯性因子的最大值与最小值，经多次测验分别设定为ωmax=0.8、ωmin=0.5；ω1—新蜜源靠近原蜜源与邻域蜜源的速度，ω2—新蜜源靠近种群最优蜜源的速度。

由式（4）可见，当t=0时，ω1和ω2分别趋于最小和最大值；当t=tmax时，ω1和ω2恰好趋于最大和最小值。刚开始迭代时ω2较大，此时寻找蜜源种群最优解的速度较快，从而大幅提高收敛速度；随着不断地迭代使得ω1和ω2进行非线性的变化，此时明显ω1大于ω2，在降低最优解对于搜索的影响的前提下，即加大随机蜜源的影响，使得种群的多样性得以保证，从而跳出局部最小值；再经局部精细搜索以获得更高的收敛精度，从而实现较好的动态平衡，大大提高寻优能力。

3 改进人工蜂群优化BP网络算法的实现

基于IABC-BP的短期负荷预测算法流程图，如图1所示。

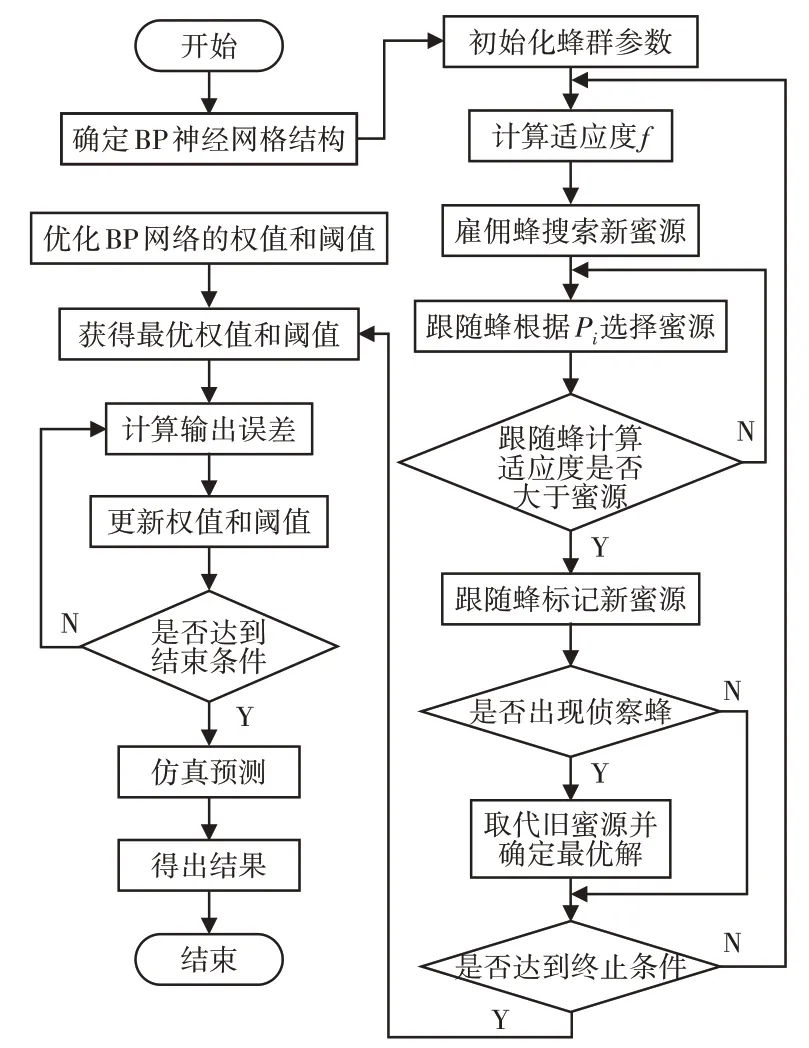
图1 IABC算法在负荷预测中的流程图Fig.1 Flow Chart of IABC Algorithm in Load Forecasting

具体实现步骤如下：

（1）利用高斯滤波将负荷数据等进行平滑预处理。

（2）确定神经网络拓扑结构。

（3）初始化蜂群。随机产生T个初始蜜源（初始解），设定蜂群大小，最大迭代次数，限制参数limit等，其中每个蜜源的位置对应为一组权值与阈值。

（4）雇佣蜂搜寻新蜜源，按式（4）在邻域内寻找蜜源。

（5）设置适应度函数。适应度函数计算公式为：

式中：fi—第i个蜜源对应网络训练的平均绝对百分误差（MAPE）。显然，当适应度达到1时为最理想的状态。

跟随蜂对选择的蜜源邻域进行搜索并按适应度的大小以式（2）确定新蜜源的位置，通过计算其所选蜜源的适应度大小判断是否需要替代。具体为若适应度大于原蜜源进行取代，若小于则该蜜源被舍弃。

（6）若蜜源被更新limit次后仍无法改进时出现侦察蜂并按（4）寻找新蜜源。

（7）重复迭代该过程检查是否达到终止条件，即达到最大迭代次数则终止，循环结束。

（8）将全局最优的蜜源对应参数作为网络的连接权值与阈值，并进行训练及预测。

4 基于IABC-BP神经网络的短期负荷预测

4.1 预测模型的网络拓扑结构

BP神经网络选择三层结构已具有逼近任意非线性函数的能力[8]，采用单隐含层的三层BP神经网络结构。

结合短期负荷特性，不难发现负荷波动与气象因素紧密联系[9-10]。不同于其他文献单一的研究某一种气象情况对负荷变化的影响，预测模型融合与预测相关的关键因素，确定为温度、湿度、风速以及日期类型。其中，气象因素对负荷的影响主要体现在两者之间存在强相关性，气象突变会导致负荷随之突变；日期类型对负荷的影响主要体现在周内、周末与节假日之间的用电量差距。因此，网络设定36个输入节点和24个输入节点，具体如表1、表2所示。

表1 网络模型输入样本定义Tab.1 Network Model Input Sample Definition

表2 网络模型输出样本定义Tab.2 Network Model Output Sample Definition

为保证最佳效果，通过网络训练选取训练误差和训练步数都较好的隐含层节点个数，综合考虑后确定隐含层节点为50个，网络激活函数为sigmoid，由此进行训练。

4.2 数据的预处理

历史负荷数据来自某地区供电公司用电信息采集系统。系统存在故障或不同表计终端传输同步误差等原因都会造成历史数据曲线有缺失或毛刺，直接输出预测网络会使预测结果产生偏差，因此在网络训练前要先对异常数据进行预处理。高斯滤波是一种线性平滑滤波，利用高斯滤波以去除数据可能存在的噪声，即平滑处理负荷数据，从而在不影响模型预测精度的前提下大幅提高预测速度及精度。为消除变量之间数量级的差别避免造成预测误差，还需将修正后数据采用MATLAB 中的mapminmax 函数分别进行归一化和反归一化处理。除此之外，短期电力负荷受气象、日期类型等因素的影响尤为明显，对此根据不同影响因素与负荷变化规律存在的差异性，也需进行归一化处理。

4.3 预测结果的分析

选取预测输出值与实际值的平均绝对百分误差（MAPE）、均方根误差（RMSE）验模型预测效果，两者定义如下。对三种模型结果进行比较，以此来验证改进算法建立短期负荷预测模型的可行性和优越性。

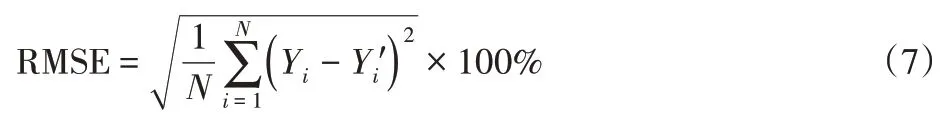
式中：N—预测样本数；Yi与—对应预测值和实际值。

5 实例验证与分析

以某地区2016年7月1日至2017年7月31日的历史负荷数据以及气象数据为基础，并从中选取8：2的比例用于样本的训练和测试，再进行负荷预测的仿真实验。

相关参数设置：取蜂群规模为200；雇佣蜂与跟随蜂的数量均为100；初始蜜源（被优化问题的初始解）的个数也为100；规定limit为超过120次，雇佣蜂转化为侦察蜂；算法的最大迭代次数为1000。

5.1 验证IABC-BP算法的辨识精度

仿真实验中，在ABC-BP和IABC-BP这两种模型下同样迭代200次，其均方根误差与迭代次数关系曲线，如图2所示。均方根误差值越小，则表示预测值越接近真实值。由图2可知，ABCBP算法迭代125次后陷入局部最小值并且停滞，而改进后算法迭代开始时均方根误差值迅速下降，迭代63次后便趋于稳定且误差明显较小，可见IABC-BP网络收敛速度更快，寻优精度更高。

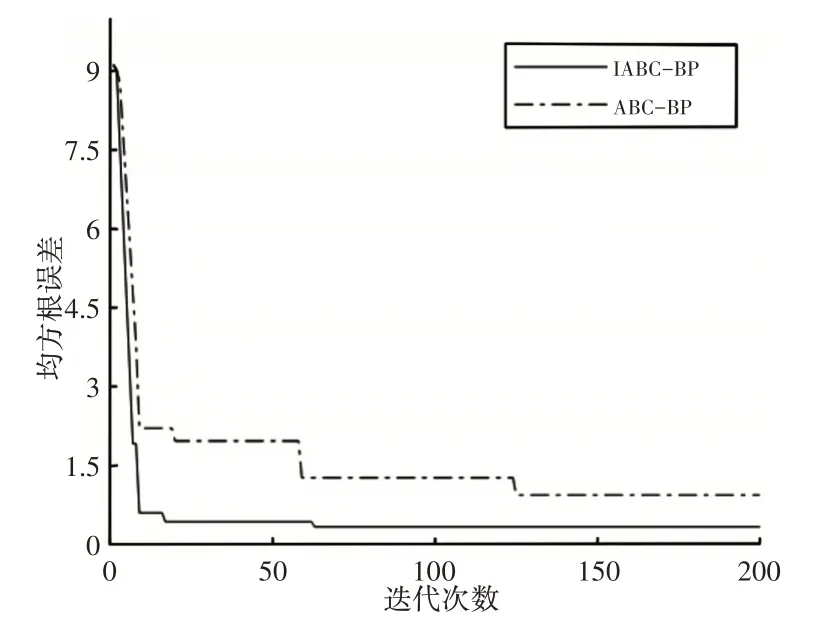
图2 均方根误差与迭代次数关系曲线Fig.2 Root Mean Square Error and Iteration Number Relationship Curve

5.2 预测模型训练性能的对比

采用单一BP 网络、ABC-BP 和IABC-BP 三种预测模型，分别对8月1日～8月7日连续一周的电力负荷进行预测，预测结果，如图3、图4所示。

图3 8月1日～8月7日实际和预测的电力负荷Fig.3 Actual and Predicted Electrical Load from 8.1～8.7

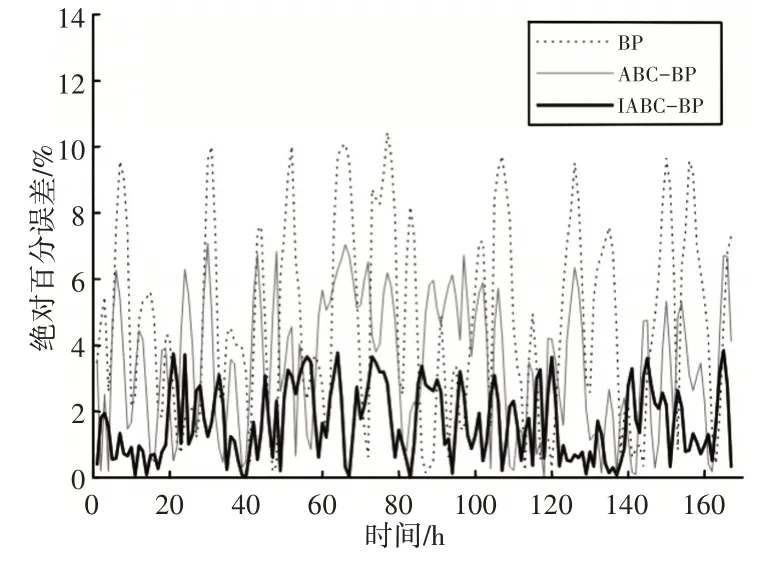
图4 8月1日～8月7日负荷预测的绝对百分误差Fig.4 Absolute Percentage Error of Load Forecast from 8.1～8.7

由图3和图4可以直观的看出：与ABC-BP、BP网络相比，采用这里方法得到的预测值最接近实际值，整体负荷曲线较为平滑，预测的绝对百分误差波动幅度较小，表现出较强的稳定性。

通过统计分析，模型的平均绝对误差和最大相对误差的计算结果，如表3所示。

表3 模型训练结果性能对比Tab.3 Performance Comparison of Model Training Results

从表3可以看出，IABC-BP预测效果最好，平均绝对误差只有1.558%，即使是最大误差也在4%左右。相比而言，BP、ABCBP的预测效果不够理想。

为进一步检验预测模型的预测效果，再分别采用上述三种模型对2017年8月29日24个时刻的电力负荷进行预测。该天实际和预测的负荷值及绝对百分误差，如图5、图6所示。

图5 8月29日24h实际和预测的电力负荷Fig.5 Actual and Predicted Electrical Load at 24h on 8.29

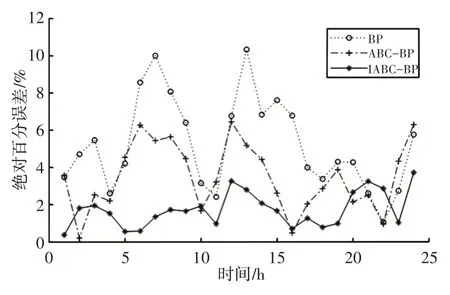
图6 8月29日24h负荷预测的平均绝对误差Fig.6 Average Absolute Error of 24h Load Forecast on 8.29

由图5和图6可以看出IABC-BP的预测误差集中在1.5%附近，说明预测具有精准性和稳定性；ABC-BP的预测误差在4%左右，表现出某些时段高低不稳定的情况；单一BP的预测误差波动较大，再次表明BP网络容易陷入局部最优，降低了预测可靠性。为了更直观的分析，将三种预测模型的平均绝对百分误差（MAPE）和均方根误差（RMSE）进行对比，计算结果，如表4所示。由表可知，采用这里方法的平均绝对误差为1.353%，比BP模型、ABC-BP模型分别小了4.570%、2.279%。而均方根误差代表着预测的稳定性，明显看出IABC-BP的预测更趋于稳定。同时，因为该模型采用了改进人工蜂群算法进行神经网络参数的优化选择，最优的参数已经设置完成，故收敛速度也得到了很大提升。

表4 8月29日24小时预测结果的误差比较Tab.4 Error Comparison of 24-Hour Forecasting Results on 8.29

6 结论

（1）通过改进搜索位置更新方案改善人工蜂群的寻优性能，再利用IABC实现网络初始参数权值和阈值的优化，以避免预测结果波动大和精度略低的缺陷。（2）融合负荷数据和气象、日期类型等核心因素数据并进行高斯滤波处理，进而构建模型应用于短期负荷预测。仿真结果表明IABC-BP预测精度与收敛速度均有大幅提高。（3）通过供电公司实例验证，可知IABC-BP算法平均绝对误差为1.353%，相较于ABC-BP、单一BP网络具有更好的精准性和可靠性，可应用于电力系统优化调度中，满足工程实际需要。