Radial Basis Function Interpolation and Galerkin Projection for Direct Trajectory Optimization and Costate Estimation
2021-07-26HosseinMirinejadTamerInancSeniorandJacekZurada
Hossein Mirinejad,, Tamer Inanc, Senior, and Jacek M. Zurada,
Abstract—This work presents a novel approach combining radial basis function (RBF) interpolation with Galerkin projection to efficiently solve general optimal control problems. The goal is to develop a highly flexible solution to optimal control problems,especially nonsmooth problems involving discontinuities, while accounting for trajectory accuracy and computational efficiency simultaneously. The proposed solution, called the RBF-Galerkin method, offers a highly flexible framework for direct transcription by using any interpolant functions from the broad class of global RBFs and any arbitrary discretization points that do not necessarily need to be on a mesh of points. The RBFGalerkin costate mapping theorem is developed that describes an exact equivalency between the Karush–Kuhn–Tucker (KKT)conditions of the nonlinear programming problem resulted from the RBF-Galerkin method and the discretized form of the firstorder necessary conditions of the optimal control problem, if a set of discrete conditions holds. The efficacy of the proposed method along with the accuracy of the RBF-Galerkin costate mapping theorem is confirmed against an analytical solution for a bangbang optimal control problem. In addition, the proposed approach is compared against both local and global polynomial methods for a robot motion planning problem to verify its accuracy and computational efficiency.
I. INTRODUCTION
DIRECT methods are extensively used for solving optimal control problems, mainly due to their ability to handle path constraints, robustness to initial guess of parameters, and greater radii of convergence compared to indirect methods[1]–[3]. Direct transcription is based on approximating states and/or controls with a specific function with unknown coefficients and discretizing the optimal control problem with a set of proper points (nodes) to transcribe it into a nonlinear programming (NLP) problem. The resulting NLP can then be efficiently solved by NLP solvers available. Many direct methods are collocation-based approaches using either local or global polynomials depending on the type of function used in the approximation. Runge-Kutta methods [4], [5] and Bspline approaches [6], [7] are examples of local collocation methods that leverage low-degree local polynomials for the approximation of states and controls. The main drawback of these methods is their algebraic convergence rate, so their solution is not usually as accurate as the solution of global polynomial methods [3].
Pseudospectral (PS) methods [8]–[14], on the other hand,use a high-degree global polynomial for the approximation of states and controls and a set of orthogonal nodes associated with the family of the polynomial for the discretization of the optimal control problem. Due to their spectral (exponential)accuracy and ease of implementation, PS methods have been widely used for direct trajectory optimization in recent years[1], [3]. However, their spectral accuracy only holds for sufficiently smooth functions. If the problem formulation or the optimal solution contains discontinuities (nonsmoothness),PS methods will converge poorly even with a high-degree polynomial [2]. Also, the use of a PS method is limited to a specific mesh of points; For instance, the Gauss PS [11]method can only use Legendre-Gauss nodes, or the Legendre PS method [12] is tied with the Legendre-Gauss-Lobatto nodes for the problem discretization. This limitation becomes problematic when the optimal solution has discontinuities requiring denser nodes around them to accurately capture the switching times of the solution, as will be later demonstrated in Section V. Variations of PS methods were proposed in the literature [15]–[18] to overcome this issue, but such modified PS schemes impose new limitations to the mathematical formulation of the problem, are usually sensitive to the initial guess of parameters, and cannot typically find an accurate solution to non-sequential optimal control problems [15], [19].Thus, a significant gap exists in the literature with respect to a computationally efficient numerical approach that can find high accuracy solution tononsmoothoptimal control problems without applying further limitations to the problem and this work intends to address it.
This paper presents a novel optimal control approach that employs global radial basis functions (RBFs) for the approximation of states and controls and arbitrarily selected points for the problem discretization. The proposed solution,called the RBF-Galerkin, combines the RBF interpolation with Galerkin projection for direct trajectory optimization and costate estimation. Since the global RBFs comprise a broad class of interpolating functions, including Gaussian (GA)RBFs, multiquadrics (MQ), and inverse multiquadrics (IMQ),the proposed method offers a great flexibility in terms of basis functions (interpolants) for parameterizing an optimal control problem. In addition, unlike a PS method tied with specific type of points, the proposed method leverages a completely arbitrary discretization scheme—which do not even need to be on a mesh of points— providing a highly efficient framework for solving nonsmooth optimal control problems such as a bang-bang problem [16], as will be later demonstrated in Section V. It should be noted that there have been recent attempts at leveraging global RBFs as the interpolants in direct transcription methods [20]–[25], but the use of RBFs was limited to specific type of problems (e.g., quadratic problems [20]) and specific discretization points (e.g.,Legendre-Gauss-Lobatto points [21]–[25]). In contrast, the proposed method leverages a completely arbitrary discretization scheme and can be used in solving any general optimal control problems. In addition, unlike many direct methods, including previous RBF-based approaches[20]–[25], the RBF-Galerkin method possesses proof of optimality for solving optimal control problems. It will be shown through theRBF-Galerkin costate mapping theoremin Section IV that there will be an exact equivalency between the Karush-Kuhn-Tucker (KKT) multipliers of the NLP resulted from the RBF-Galerkin method and the discretized form of the costates of the original optimal control problem, if a set of discrete conditions (closure conditions) holds.
The major contribution of this work is to present a highly flexible numerical solution to general optimal control problems, especially the nonsmooth problems whose formulation or optimal solution involves discontinuities that cannot be accurately estimated by classical optimal control methods. Another contribution is the proof of optimality viaRBF-Galerkin costate mapping theoremguaranteeing that the solution of the proposed method is equivalent to the solution of the original optimal control problem. To the best of the authors’ knowledge, this is the first time that ahighly flexible,
computationally efficient,accuratesolution with theproof of optimalityis presented for general optimal control problems.
The rest of the paper is organized as follows: A general optimal control problem is formulated in Section II. The RBFGalerkin solution is described in Section III. The costate estimation along with the proof of optimality is presented in Section IV. Numerical examples are provided in Section V,and finally, the conclusions are drawn in Section VI.
II. OPTIMAL CONTROL PRObLEM FORMULATION
The general optimal control problem is defined in Bolza form [3] as to determine the statex(τ)∈Rn, controlu(τ)∈Rm,initial timet0, and final timetfthat minimize the cost functional
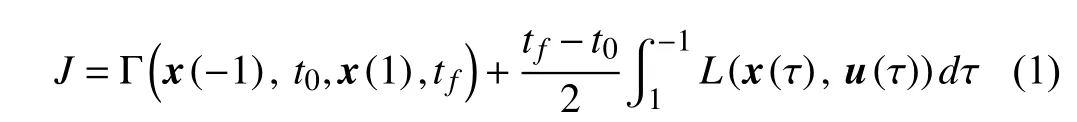
subject to state dynamics,

III. RBF-GALERkIN METHOD FOR DIRECT TRAjECTORY OPTIMIZATION
A direct method combining global RBF parameterization,Galerkin projection, and arbitrary discretization is proposed to discretize the optimal control problem of (1)–(4). The discretized problem can be solved with the NLP solvers available.
RBF Definition:RBF is a real-valued function whose value depends on the distance from a fixed point, called center [26]

where ρ,y,c, and ‖‖ denote the RBF, function variable, RBF center, and the Euclidean norm, respectively. Any function satisfying (6) is called an RBF function, which can be either infinitely smooth such as GA, MQ, and IMQ RBFs, or piecewise smooth such as Polyharmonic Splines. Infinitely smooth RBFs are also called global RBFs.
In the proposed method, global RBFs are leveraged as the basis functions for parameterizing the optimal control problem. For brevity and without loss of generality, it is assumed that the same type of RBFs, ρ, and the same number of RBFs,N, are used for the approximation of statesx(τ) and controlsu(τ) as


fori=1,...,Nandj=1,...,N, wherewkare the same quadrature weights used in (13). By applying the same numerical quadrature to approximate the running costLin (1),the optimal control problem of (1)–(4) is transcribed into the following NLP problem:

The proposed method is flexible in terms of both interpolant functions and discretization points, as it can use any type of global RBFs as the interpolants and any arbitrary-selected points as the discretization points. The arbitrary discretization scheme is based on the fact that the RBF interpolation is always unique for global RBFs, regardless of the type and number of points used in the interpolation [26].
IV. COSTATE ESTIMATION
In this Section, it will be shown that the KKT optimality conditions of the NLP problem of (17) and (18), are exactly equivalent to the discretized form of the first-order necessary conditions of the optimal control problem of (1)–(4), if a set of conditions will be added to the KKT conditions.
A. KKT Optimality Conditions
Lagrangian or augmented cost of the NLP problem is written as


Similarly,
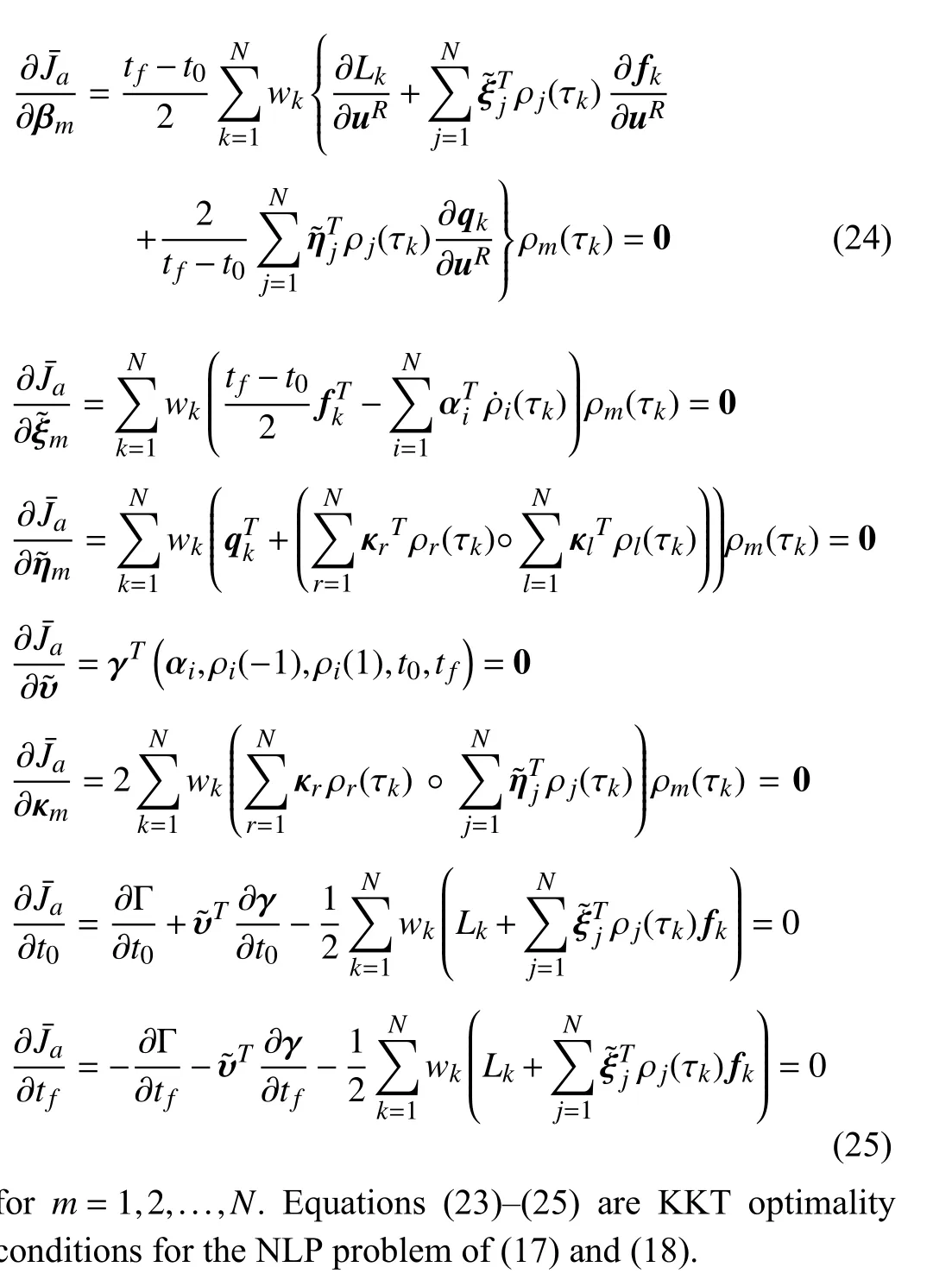
B. First-Order Necessary Conditions of the Optimal Control Problem
Assuming λ(τ)∈Rnis the costate, and µ(τ)∈Rqis the Lagrange multiplier associated with the path constraints,Lagrangian of the Hamiltonian (augmented Hamiltonian) of the optimal control problem of (1)–(4) can be written as


C. RBF-Galerkin Discretized Form of First-Order Necessary Conditions
The first-order necessary conditions of (27) are discretized using the RBF-Galerkin method. To this end, the costates λ(τ)∈Rnand Lagrange multipliers µ(τ)∈Rqare approximated usingNglobal RBFs as

where λR(τ) and µR(τ) are the RBF approximations ofλ(τ)and µ(τ). Also, ξjand ηjare the RBF weights for λR(τ) andµR(τ), respectively. By using (7), (8), and (14) along with (28)and (29), the first-order necessary conditions of (27) are parameterized with the global RBFs. Then, applying the Galerkin projection to the residuals and approximating the Galerkin integral with a numerical quadraturediscretizethe first-order necessary conditions as


D. Costate Mapping Theorem
So far, two sets of equations were derived corresponding to two different problems: The KKT optimality conditions of the RBF-Galerkin method shown by (23)–(25) in Section A and the discretized form of the first-order necessary conditions of the optimal control problem described by (30)–(33) in Section B. It was shown in the literature [3], [9] that dualization and discretization are not commutative operations, in general. In fact, when a continuous-time optimal control problem is discretized, a fundamental loss of information occurs in either primal or dual variables. Similar to the costate mapping theorem previously shown in the literature for PS methods[11], [28], [29], the RBF-Galerkin costate mapping theorem is developed here to restore this loss of information by adding a set of discrete equations to the problem defined in Section A.
To provide an exact equivalency between the KKT optimality conditions of the NLP derived from the RBFGalerkin method and the discretized form of the first-order necessary conditions of the optimal control problem, a set of conditions must be added to (23)–(25). These conditions are

Discrete conditions of (34) and (35) are known asclosure conditionsin the literature [28], [29] and applied to the costates and Hamiltonian boundaries to guarantee that firstorder necessary conditions of the NLP (i.e., KKT conditions)are equivalent to the discretized form of the first-order necessary conditions of the optimal control problem. In other words, by adding (34), (35) to the KKT conditions, the dualization and discretization are made commutative and hence the solution of the direct method is the same as the solution of indirect method.
RBF-Galerkin Costate Mapping Theorem:There is an exact equivalency between the KKT multipliers of NLP derived from the RBF-Galerkin method and Lagrange multipliers(costates) of the optimal control problem discretized by the RBF-Galerkin method.
Lemma 2:The Lagrange multipliers of the optimal control problem can be estimated from the KKT multipliers of NLP at discretization points by the equations

Proof:Substitution of (36) in (31), (32), and (33) proves that (23)–(25) and (30)–(33) are the same, and hence the equivalency condition holds. ■
V. NUMERICAL EXAMPLES
Two numerical examples are provided to demonstrate the efficiency of the proposed method. Example 1 is a bang-bang optimal control problem for which an analytical solution is available. The optimal trajectories calculated by the RBFGalerkin method are evaluated against the exact solutions.Also, the costates computed by the RBF-Galerkin costate mapping theorem are compared against the exact costates from the analytical approach. Bang-bang is a typical nonsmooth optimal control problem in which the optimal solution has a switching time needed to be accurately estimated. Therefore, the efficacy of the RBF-Galerkin approach in solving a nonsmooth optimal control problem as well as the accuracy of the RBF-Galerkin costate mapping theorem will be thoroughly investigated in this Example.
Example 2 is a robot motion planning problem with obstacle avoidance in which the optimal trajectories from the RBFGalerkin method are evaluated against those calculated from the two existing optimal control methods: DIDO [30], a commercial optimal control software tool using Legendre PS method (global polynomial), and OPTRAGEN [31], an academic optimal control software package using B-Spline approach (local polynomial) for direct trajectory optimization.Comparison studies between the proposed approach and the existing methods are presented to demonstrate the superior performance of the RBF-Galerkin solution for a typical motion planning problem.
A. Example 1
Consider a bang-bang optimal control problem with quadratic cost as to minimize

This example was thoroughly investigated in [16], in which the authors concluded that a PS method in the classic form cannot accurately solve it due to the discontinuity of the optimal control. For instance, it has been shown that the switching time of the solution cannot be accurately estimated from the Chebyshev PS method of [10] and the numerical solution from the PS method includes undesired fluctuations at the boundaries (see [16] for more details).
On the other hand, modified PS schemes [15]–[18] may provide better performance than their classic counterparts for solving nonsmooth optimal control problems. However, they suffer from serious constraints limiting their applicability for solving such problems. For instance, a modified PS technique is more prone to the initial guess of parameters (reduced robustness), imposes higher computational loads, and can only handle limited form of state dynamics (i.e., dynamic constraints must be converted to explicit or implicit integral form), compared to a classic PS method [15].
In light of the current limitations with the existing methods,we investigated the efficiency of the RBF-Galerkin method for solving the nonsmooth optimal control problem of (37)and (38). To leverage the capability of arbitrary discretization of the proposed method, a set of pseudorandom points along with the trapezoidal quadrature was chosen for the discretization. 40 randomly distributed points were selected in the interval [0 5] from which at least five points were located between [1.2 1.3]. Increasing the density of discretization points around the discontinuity, i.e.,t=1.275, which is not typically possible in other direct methods, enhances the performance of the RBF-Galerkin method in accurately capturing the switching time of the solution. By parameterizing the states and control with the IMQ RBFs and applying the aforementioned discretization points, the problem of (37) and (38) was transcribed into an NLP, which was solved by SNOPT [32], a sparse NLP solver, with default feasibility/optimality tolerances ( ≈10-6).

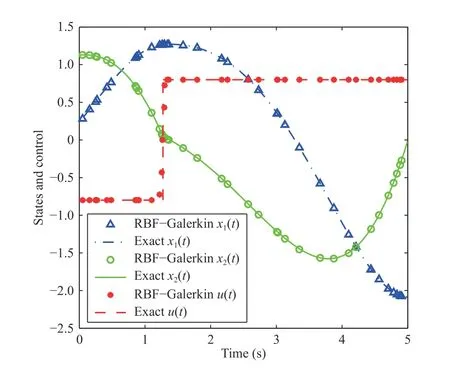
Fig. 1. States and control trajectories calculated by the RBF-Galerkin method for 40 pseudorandomly distributed points along with the exact solutions.

Fig. 2. Costates computed by the RBF-Galerkin costate mapping theorem along with the exact costates for 40 pseudorandomly distributed points.

B. Example 2
A robot motion planning problem with obstacle avoidance in 2-dimensional space is considered. It is desired to find an optimal trajectory for a mobile robot that spends minimum kinetic energy to navigate through three circular obstacles in a fixed time span [0 20]. The obstacles are located at (40,20),(55,40), and (45,65) with the radiusr=10. The horizontal and vertical speeds of the mobile robot cannot exceed 10. The optimal control problem is formulated as to minimize the cost function

subject to the constraints
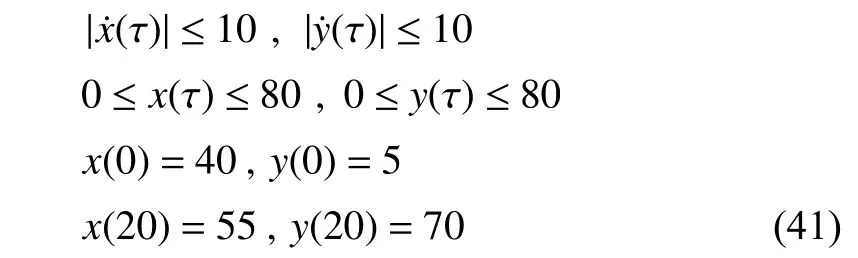
and nonlinear path constraints (obstacles)
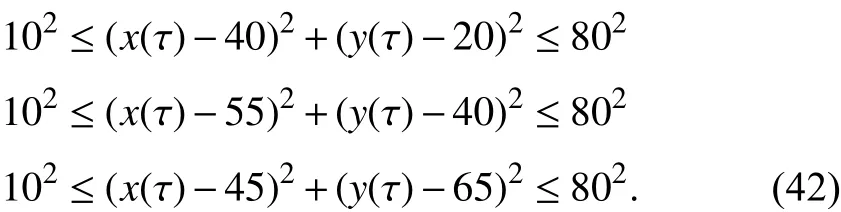
The optimal trajectory for the mobile robot was computed from three different methods: The RBF-Galerkin approach,Legendre PS method (DIDO), and B-Spline approach(OPTRAGEN). All three methods use the same environment(MATLAB) along with the same NLP solver (SNOPT). To conduct a fair comparison, Legendre-Gauss-Lobatto points–type of points used in the Legendre PS method – were incorporated in the other two methods, as well. The cost and computation time of each method are demonstrated in Table I for different number of discretization points, i.e.,N= [10, 20,30].
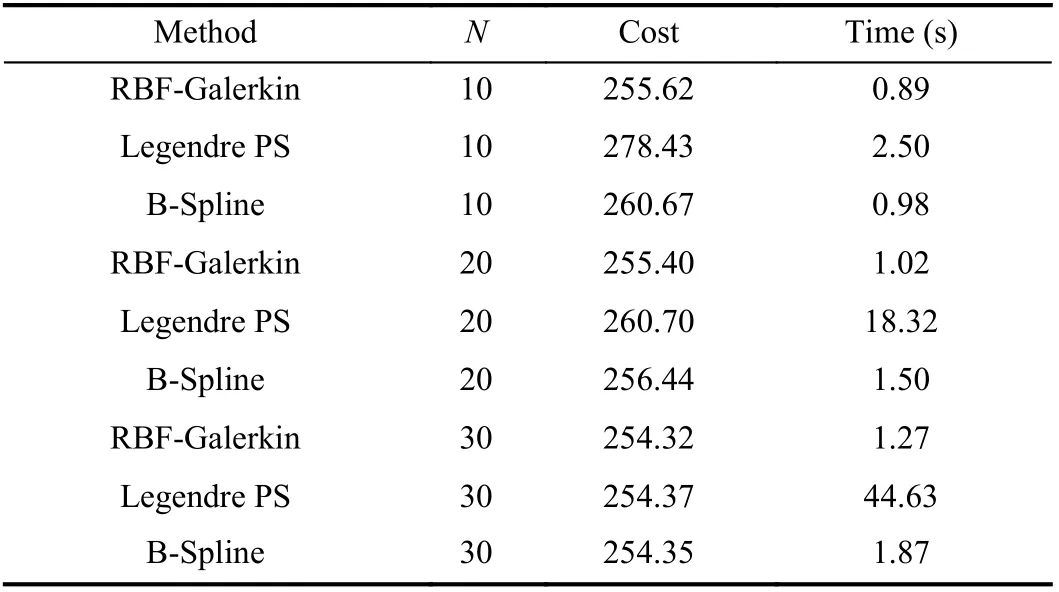
TABLE I COST AND COMPUTATION TIME OF RBF-GALERkIN, LEGENDRE PS,AND B-SPLINE METHODS FOR RObOT MOTION PLANNING EXAMPLE FOR N = [10, 20, 30]
By increasing the number of discretization points, the accuracy of trajectories improves at the expense of higher computation time. Among the three methods, the RBFGalerkin had the least cost value and the shortest computation time for each value ofN. For instance, the cost function from the RBF-Galerkin approach forN= 10 had about 2% and 8%less value (more accurate) than the B-Spline and Legendre PS method, respectively. Also, the computation time of the RBFGalerkin approach was 9% faster than B-Spline and about 64% faster than Legendre PS method for the same number of discretization points. The computational efficiency of the RBF-Galerkin method is more profound forN= 20 andN=30. This comparison studies clearly demonstrate superior accuracy and computational efficiency of the proposed approach against the state of the art in a motion planning example. The optimal trajectory calculated by the RBFGalerkin approach forN= 30 is shown in Fig. 3.
VI. CONCLUSION

Fig. 3. Optimal trajectory estimated by RBF-Galerkin method for robot motion planning with obstacle avoidance, N = 30.
The RBF-Galerkin method combining RBF interpolation with Galerkin projection was presented for solving optimal control problems numerically. The proposed method incorporates arbitrary global RBFs along with the arbitrary discretization scheme offering a highly flexible framework for direct transcription. The RBF-Galerkin costate mapping theorem was developed through which the costates of the optimal control problem can be exactly estimated from the KKT multipliers of NLP at the discretization points. The efficacy of the proposed method for computing the states,costates, and optimal control trajectories as well as accurately capturing the switching time of the control function was verified through a bang-bang example for which an exact solution was available. Also, the superior accuracy and computational efficiency of the RBF-Galerkin approach were confirmed against a local and a global polynomial method for a motion planning example with obstacle avoidance. As the future extension, it is suggested to find an automated strategy to fine-tune the design parameters of global RBFs, including free shape parameter, to minimize the RBF interpolation error and promote the overall performance of the RBF-Galerkin approach.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Distributed Subgradient Algorithm for Multi-Agent Optimization With Dynamic Stepsize
- Kernel Generalization of Multi-Rate Probabilistic Principal Component Analysis for Fault Detection in Nonlinear Process
- Learning Convex Optimization Models
- An RGB-D Camera Based Visual Positioning System for Assistive Navigation by a Robotic Navigation Aid
- Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids
- Cooperative Multi-Agent Control for Autonomous Ship Towing Under Environmental Disturbances
