Kernel Generalization of Multi-Rate Probabilistic Principal Component Analysis for Fault Detection in Nonlinear Process
2021-07-26DongleiZhengLeZhouandZhihuanSong
Donglei Zheng, Le Zhou,, and Zhihuan Song
Abstract—In practical process industries, a variety of online and offline sensors and measuring instruments have been used for process control and monitoring purposes, which indicates that the measurements coming from different sources are collected at different sampling rates. To build a complete process monitoring strategy, all these multi-rate measurements should be considered for data-based modeling and monitoring. In this paper, a novel kernel multi-rate probabilistic principal component analysis (KMPPCA) model is proposed to extract the nonlinear correlations among different sampling rates. In the proposed model, the model parameters are calibrated using the kernel trick and the expectation-maximum (EM) algorithm. Also, the corresponding fault detection methods based on the nonlinear features are developed. Finally, a simulated nonlinear case and an actual predecarburization unit in the ammonia synthesis process are tested to demonstrate the efficiency of the proposed method.
I. INTRODUCTION
WITH the continuous developments of modern process industries and advances of data acquisition technologies, a large amount of industrial process data have been collected and stored by the distributed control system (DCS),which made data-driven process monitoring methods become a hot research topic in the field of process control in recent years [1]–[7]. Especially, with the rapid developments of machine learning and deep learning in recent decades,multivariate statistical process method (MSPM) technology can accurately express the operation state of processes at a low cost while also being easy to apply. Therefore, MSPM methods like principal component analysis (PCA), partial least squares (PLS) and their extensions have been widely applied in various types of process industries [8]–[12]. Besides, the process data are usually measured with different kinds of noises, which have an obvious impact on the data-driven model. Hence, the descriptions of the process noises should also be considered for process modeling purposes. At the same time, the process measurements are inherently stochastic variables instead of the deterministic values, which indicate that they are proper to be estimated in a probabilistic manner.Ge [13] has made a review of various types of probabilistic latent variable models in recent years, in which probabilistic PCA (PPCA), factor analysis (FA), and Gaussian mixture model (GMM) are widely used for process modeling and monitoring [14]–[16].
For most traditional MSPM methods, they all assumed that the sampled numbers of the training data for different variables are consistent. However, as the process industries have become more and more complex and production scales increase, the integrated automation system has been split into multiple levels and multiple sampling rates of the measurements are contained [17]–[19]. For example, the sampling rates of the process variables such as temperature,pressure, and flow are usually around a few seconds or minutes. Some important quality variables and other scheduling related data are tested at the laboratory with a much lower sampling rate, such as the product quality,exhaust gas concentration, and energy consumption index.They may be collected among a few hours or days. In general,various variables with different sampling rates from multiple levels can reflect the process status from different perspectives. Hence, it is desirable to utilize all the sampled measurements which are collected from multiple sampling rates so that different unfavorable conditions of processes like sensor faults, quality decline, or excessive energy consumption can be accurately detected and identified.
The traditional data-driven methods for multi-sampling rate process monitoring can be summarized as up-sampling methods, down-sampling methods, and semi-supervised methods. The main idea of the up-sampling method is to establish a regression model to predict the un-sampled data with a lower sampling rate. For comparison, the downsampling method is to reduce all the variables to the lowest sampling rate to transfer a multiple sampling rate process to a single sampling rate process. After these two pretreatment technologies, the traditional MSPM method can be applied for process modeling and monitoring. Luet al. [20] transformed the original dual sampled data into a three-dimensional matrix by adjusting the sample structure and using a multiway PLS model for key variable prediction. Marjanovicet al. [21]extended the process variables with different sampling scales to the high-dimensional vectors according to the sampling interval of the quality variable. After that, the batch process monitoring scenario is established using the down-sampled data. Besides, Liet al. [22] used fast sampling and slow sampling samples through the lifting technology and resampling for batch process modeling. However, there are still several limitations to these methods. Up-sampling methods greatly depend on the accuracy of the regression model. Down-sampling methods break correlations of their original data structures. When the difference between sampling rates is too large, training data will be statistically insufficient and cannot derive an accurate enough model.
Another choice for multi-rate process modeling is to directly utilize the original dataset. The probabilistic model can combine the probability inference and the expectation maximization (EM) algorithm, which makes it possible for estimating the missing data and multi-rate process modeling[23]. Especially, the semi-supervised methods have been used for quality prediction and monitoring in the dual-rate process.Geet al. [24] proposed a semi-supervised algorithm based on Bayesian canonical PPCA and a selection method of the dimension of latent variables. Zhouet al. [25] proposed a semi-supervised probabilistic latent variable regression(PLVR) model and applied it on a continuous process and batch process, in which the unbalanced fast sampling process variables and slow sampling quality indexes were both involved. Recently, the semi-supervised probabilistic model has been extended to the multi-rate form. The multi-rate PPCA and multi-rate factor analysis models are developed to incorporate the measurements with different sampling rates without down-sampling and up-sampling. Also, the common latent variables are extracted in the probabilistic framework to describe the auto-correlations among different sampling scales[26], [27].
Besides, the correlation relationships in the actual industrial processes are usually nonlinear, which indicates that linear models will be improper for these cases. To deal with the nonlinear relationship among process and quality variables,the kernel method has been widely used in many statistical learning methods such as support vector machines (SVM),kernel principal component analysis (KPCA), kernel probabilistic principal component analysis (KPPCA), kernel partial least squares (KPLS) [28]–[31], etc. Huang and Yan[32] proposed a quality-driven kernel principal component analysis (Q-KPCA) model for quality dependent nonlinear process monitoring by decomposing the kernel matrices into quality related and unrelated spaces. With the help of the kernel trick, the nonlinear correlations can be projected to be linear in the feature subspace. Besides, ensemble learning is also an idea for monitoring nonlinear processes. Li and Yan[33], [34] used the ensemble learning to solve nonlinear problems and improve monitoring performance. More recently, a deep learning technology has been rapidly developed with the enhancements of the computing hardware and the increase of the data storage capacity [35]. Using endto-end learning, the parameters of feature extraction and pattern classification in the multi-hidden layer network can be coordinated and optimized. For process modeling and monitoring purposes, deep learning technologies have also been applied. Jianget al. [36] proposed a unified robust selfmonitoring framework, which adds the artificial data into the model input and introduces the robust training method into the self-supervised model. Denget al. [37] proposed a deep learning method based on the nonlinear PCA model for industrial process monitoring and fault detection named deep PCA (DePCA). Wu and Zhao [38] performed the convolution operation on chemical industry data sets and proposed a deep convolutional neural network (DCNN) model for fault diagnosis.
In these models, the nonlinear activation functions are contained in each layer, which makes it possible to solve nonlinear problems and have good fitting abilities. However,most current deep learning models still require that the dimensions of input samples must be unified. It is hard to directly utilize the traditional deep learning models for the nonlinear multi-rate processes.
In past research mentioned above, those mainly focused on the model of single sampling rate, which led to the lack of process monitoring of multi-sampling rate data. Besides, the current multi-rate process modeling methods rarely considered the nonlinear constraint relationship. Hence, the kernel multirate probabilistic principal component analysis (K-MPPCA)model is proposed to extract the nonlinear correlations with different sampling rates. With the aid of the kernel trick, the common principal components are derived in the highdimensional feature space, in which the correlations between the principal components and the projected measurements among different sampling rates are assumed to be linear. The model parameters can also be calibrated using the EM algorithm. Moreover, the fault detection scenarios with different sampling rates are further developed in the feature space and several residual spaces for each sampling rate. The corresponding fault detection performance is expected to be more accurate since the nonlinear correlations are extracted and monitored without destroying the original multi-rate structures.
The contribution of this work can be summarized as follows:
1) The constraint nonlinear relationship with different sampling rates are considered in the proposed K-MPPCA model. Besides, a nonlinear EM algorithm is proposed for model parameter estimation since the explicit nonlinear correlations between the original measurement and the latent variables cannot be obtained after the kernel method is introduced.
2) A fault detection scheme for a nonlinear multi-rate process is developed. In K-MPPCA, however, the squared prediction error (SPE) statistics are difficult to derive in highdimensional feature space. Hence, it is further constructed with the help of the kernel trick in this paper.
The rest of this paper is organized as follows. The section“Revisit of MPPCA” briefly reviews the MPPCA model,which is linear and based on the whole multi-rate measurement. Then, the K-MPPCA model and its model parameter estimation method for the nonlinear multi-rate process are introduced in detail in “K-MPPCA Model”. “KMPPCA based Fault Detection” implements the nonlinear process monitoring strategy using the multi-rate measurements. “Case Studies” demonstrates a numerical example and an actual industrial process to evaluate the performance of the proposed method. Finally, some conclusions are made.
II. REVISIT OF MULTIPLE PRObAbILITY PRINCIPAL COMPONENT ANALYSIS
As a multi-rate form of PPCA model, MPPCA has a similar structure to PPCA and can make full use of data with different sampling rates, which is given as follows

III. KERNEL MULTIPLE PRObAbILITY PRINCIPAL COMPONENT ANALYSIS MODEL
In the actual multi-rate process, process variables often exhibit a strong nonlinear relationship which leads to poor interpretation of the loading matrices (such as{Φ1Φ2···ΦS-1ΦS}, as obtained in the MPPCA model) and has some limitations on the fault detection approach based on it. In this section, the linear MPPCA model is generalized to its nonlinear form using the kernel trick, which is named as the multi-rate probability kernel principal component analysis (KMPPCA) model. Also, its model parameter estimation methods are derived.
A. Kernel Multiple Probability Principal Component Analysis Model (K-MPPCA)
The nonlinear relationship between the multi-rate


B. Model Parameter Estimation Using Nonlinear EM

In the M-step, the exponential likelihood function is maximized, which is given as
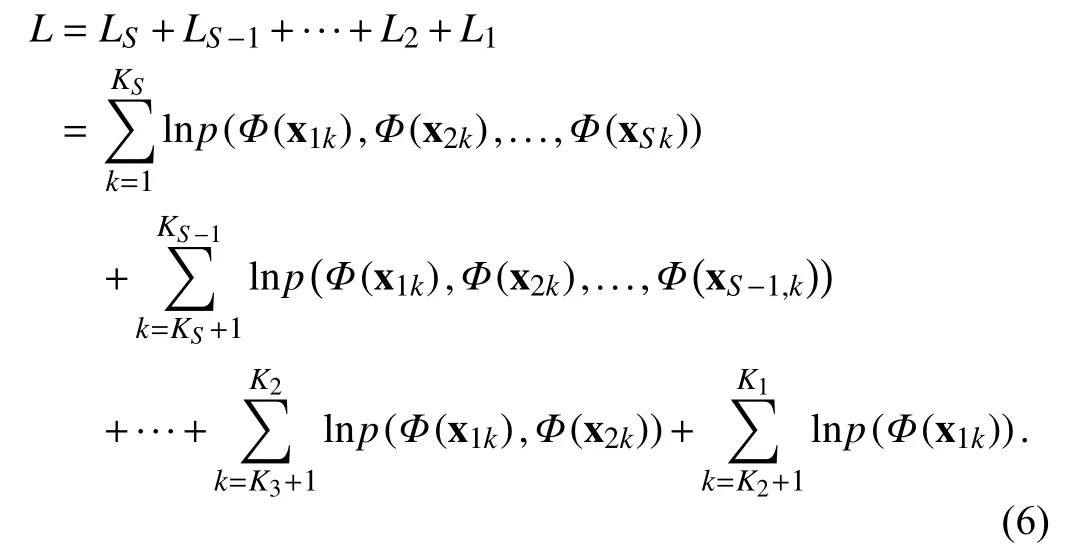
The updated model parameters value can be obtained by taking the partial derivative of the likelihood function concerning the parameter and they are estimated as

It can be readily obtained that the model parameters cannot be directly estimated using the above equations since the projected values {Φ(x1),Φ(x2),...,Φ(xS-1),Φ(xS)} are unknown. Therefore, it is necessary to introduce the kernel method by calculating the kernel matrix of different sampling variables. In such a manner, a nonlinear EM algorithm is developed.
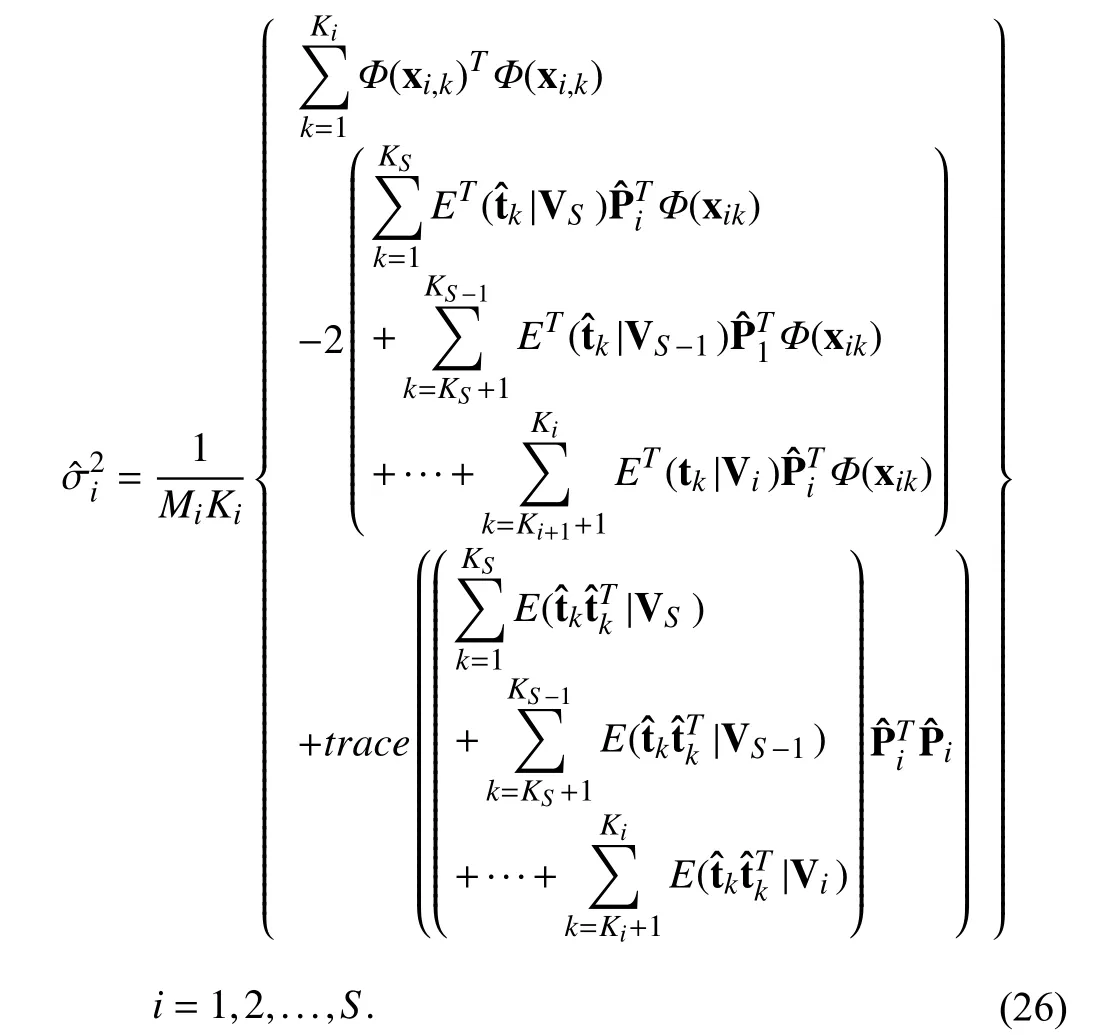
Firstly, all the loading matrices can be decomposed into three parts, which are given as follows:

At the same time, the equivalent transformation can be obtained as

By introducing the kernel trick, the K-MPPCA model avoids the problem of solving the explicit nonlinear relationships between the process variables and the latent variables. Hence, the posterior expectations of the latent variables can be obtained without loading matrices in the Estep. Because of this and the assumption that process variables and latent variables are nonlinear, the model K-MPPCA is nonlinear.
Similarly, the kernel trick can also be used to update the model parameters in the M-step, which is given as

in which trace (·) is an operator for the trace value of the matrix. The detailed derivation of the M-step is provided in Appendix A. In the nonlinear EM algorithm, the accurate model parameters can be obtained by iterating E-step and Mstep until convergence. It should be noted that theS-type measurement data in the multi-rate process were reordered and the corresponding measurement variables were given before the EM algorithm. This is for ease of tagging and coding. The model parameters estimation can still work without this step. In addition, the projected values need to be re-centralized. The specific centralized equations are
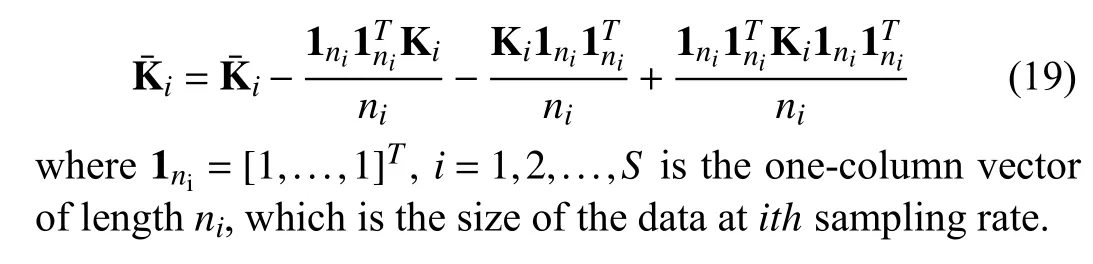
C. Discussions of K-MPPCA
In this subsection, some properties of the proposed KMPPCA models are further discussed by several remarks.
Remark 1:The proposed K-MPPCA can reduce to KPPCA whenS=1, in which the measurements with single sampling rate is used for model training. Also, K-MPPCA can reduce to supervised KPLVR (S=2 andK1=K2) or semi-supervised KPLVR (S=2 andK1≠K2). Therefore, these models can be treated as the specific forms for K-MPPCA.
Remark 2:The proposed K-MPPCA model implicitly maps the original multi-rate measurements to a higher dimension.By designing appropriate kernel parameters, the projected values turn to be linearly correlated and the constraint relationship with different sampling rate can be presented by a few linear latent variables.
Remark 3:It is noticed that the K-MPPCA model is totally different from several separated KPPCA models. The latent variables of K-MPPCA are determined by simultaneously considering all the classes of the process variables and the model parameters which are influenced by each other. It can be seen from (15)–(18) that model parameters at different sampling rate are affected by parameters of other sampling rates rather than just themselves.
IV. K-MPPCA BASED FAULT DETECTION


When the new samples are collected under different sampling rates, the expected values of the latent variables are calculated separately considering different conditions, which depend on which class of measurements it contains. The estimated mean projections of latent variables are calculated as

In addition,SPEstatistics can also be constructed based on the prediction errors of the model. Considering that the test data may have multiple sampling rates, it must designStype ofSPEstatistics forSsampling rates, which is given as
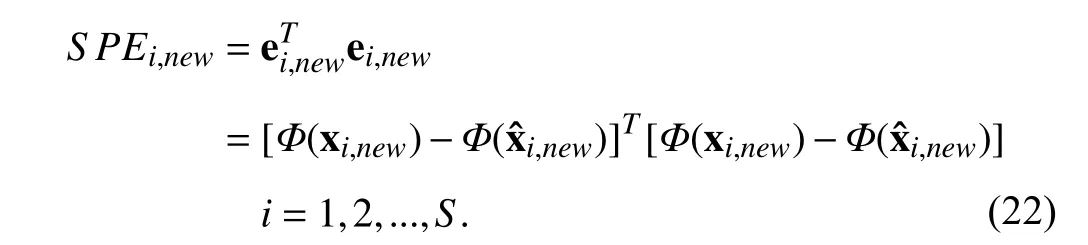
Since the projected values Φ(xi,new) cannot be directly obtained, the kernel function is also used to eliminate the inner product of the high-dimensional mapping set and they are given as



V. CASE STUDY
In this section, a numerical example and an actual predecarbonization unit in the ammonia synthesis process are tested to evaluate the process modeling and monitoring performance of the proposed method. The first one is a hypothetical example, as it is easier to understand why the proposed K-MPPCA outperforms the traditional models.Then, we applied the proposed method to a predecarbonization unit data in the ammonia synthesis process found in the chemical industry. In both cases, the process variables are highly nonlinearly correlated, in which several nonlinear process monitoring methods are compared,especially when the process sampling rates are different.
A. Numerical Example
In order to demonstrate the effectiveness of the proposed algorithm, a multi-sampling rate process is designed in this section. There are 8 variables in the system, which are obtained by a nonlinear combination of 6 latent variables. The process is given as follows:

where {x1,x2,...,x8} are process variables and {t1,...,t6} are latent variables. Besides, some small disturbances are added to simulatethemeasurementnoises(,which)areassumedto followGaussian distributionasN0,0.12I.Inthisprocess,these variables are collected in different sampling rates, where{x1,x2,...,x5} are sampled once a minute, {x6,x7} are sampled every two minutes, andx8is collected every ten minutes. In total, these variables are generated within a period of 2000 minutes, which indicates that 2000 samples of {x1,x2,...,x5},1000 samples of {x6,x7}, and 200x8have been collected. For comparison, KPPCA and Q-KPCA are also used for nonlinear process modeling and monitoring [29], [31]. Since KPPCA is based on the single sampling rate data, there are two types of data pre-processing methods used in this paper. The first one only uses the measurements with the highest sampling rate,which means that only {x1,x2,...,x5} are used for the model training. This model is named as KPPCA1. Another choice is to utilize the samples where all the variables are collected at that sampling interval. Hence, only 200 samples are obtained,which are based on the lowest sampling rate. This model is named KPPCA2. The dimension of the feature space of KMPPCA is selected as 10. The widely used radial basis function (RBF) is selected as the kernel function. The kernel parameters are chosen as 450, 30, and 0.1 for different sampling rates. To be fair, the component numbers of KPPCA1and KPPCA2are both set as 10 and their kernel parameters are both selected as 450: the same as that in the KMPPCA model with the highest sampling rate. The choice of the kernel parameters is still an open question in kernel learning methods. In this paper, the cross-validation is used for model selection and it is obtained that these three methods can achieve the best results under the same kernel parameters.Moreover, the fault detection effect of the model does not change greatly when the kernel parameters are kept within a certain range. For the Q-KPCA model, in this case,{x1,x2,...,x5} are the process variables andx8is the key quality variable in Q-KPCA. Again, only the data at the full sampling interval are utilized. The kernel parameter is set to 500 according to the cross-validation method. The dimensions of the latent variables in quality-related space and qualityuncorrelated space are set to be 1 and 50, respectively. In QKPCA,Ty2andTo2statistics are used to monitor the changes of these two spaces respectively.
For fault detection purposes, another set of samples with a period of 2000 minutes are generated, in which five kinds of faults are introduced from the 1001st minute to evaluate the fault detection performance for different models. Like most fault detection methods, bothT2and SPE statistics are used to measure the effect of fault detection in this case. The calculation methods of the control limit of two statistics have been mentioned in the previous section. If the value of the statistic is greater than the control limit, it is considered a fault. The detailed fault descriptions are given in Table I.

TABLE I FAULT DESCRIPTION IN THE NUMERICAL EXAMPLE
In this paper, the false alarm rates and missing detection rates of faults are used to qualify the process monitoring results. Among them, false alarm rates refer to the proportion of normal samples identified as fault samples, while missing detection rates refer to the proportion of fault samples detected as normal samples. Given a significance level of 99 percent, the detailed fault detection results are given in Table II.
The lower false alarm and missing detection rate, the better the model performance. The results with better detection performance are highlighted in bold and the fault 0 data is the false alarm rate of these three models.


TABLE II MONITORING RESULTS IN THE NUMERICAL EXAMPLE
In addition, theSPEstatistics are separately built for different sampling rates for the K-MPPCA based fault detection strategy since the measurements with multiple sampling rates are usually collected from different sources,such as process and quality variables. Hence, such a design will be helpful for further fault identification. For example,Fault 4 and Fault 5 are about the process variablesx7andx8.However, KPPCA1did not use variablesx7andx8during modeling. Hence, the fault aboutx7andx8will not be detected using KPPCA1.
In practice, such faults are similar to the sensor faults, which often exist and whose sampling rate of fault variables is sometimes low. If only the highest-sampling-rate data are used for modeling like KPPCA1, such faults will not be detected totally, which will cause great damage. Hence, this situation also highlights the advantages of our proposed KMPPCA over KPPCA1which are shown in Fig. 2.
In addition, since differentSPEstatistics are established for variables with different sampling rates, the K-MPPCA model can indicate the specified sampling rate according to theSPEstatistics. This is also helpful for further fault identification.For KPPCA2, however, it only contained part of sampled data so that the established model is not accurate enough and the false alarm rate is too high. By contrast, theT2and statistics in the K-MPPCA model can accurately detect the potential faults with a low false alarm rate. At the same time, only theSPEstatistic at the second sampling rate has exceeded the control limit, which can be used to determine the range of variables that are causing the fault. Furthermore, it is useful for further fault identification. The detailed detection result of Fault 5 is shown in Fig. 2.
B. Pre-Decarburization Unit
The ammonia synthesis process is quite common in modern chemical industries and its product, NH3, is also the basic material for many processes, such as the urea synthesis. Predecarburization is a crucial unit to the process and its main function is to eliminate carbon dioxide (CO2) in the original process gas (PG) as much as possible. The flowchart of the pre-decarburization unit with all instruments is given in Fig. 3.
The process description and the sampling rates of measurements are tabulated in Table III.

Fig. 1. Monitoring results of Fault 1 in the numerical example by (a) KMPPCA, (b) KPPCA1, (c) KPPCA2, (d) Q-KPCA.
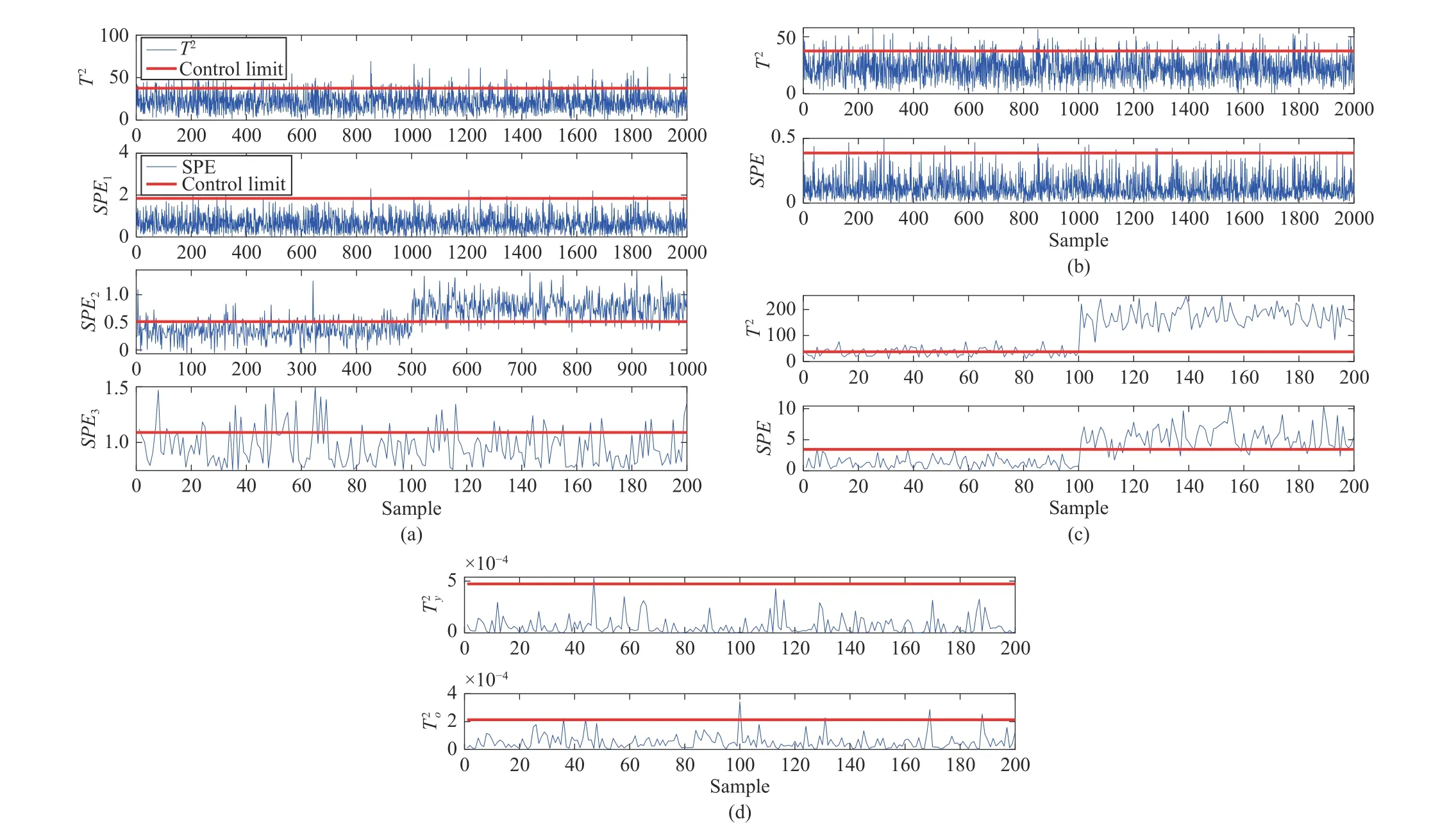
Fig. 2. Monitoring results of Fault 5 in the numerical example by (a) K-MPPCA, (b) KPPCA1, (c) KPPCA2, (d) Q-KPCA.
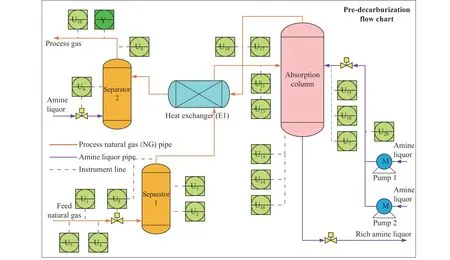
Fig. 3. Flow chart of the pre-decarbonization unit.
From the DCS database in the ammonia synthesis process, nine process variables under the normal operation condition within a period of 3000 min are collected. As shown in Table III, there are three kinds of sampling rates in these measurements, in which 4 of them are sampled per minute and the other variables are sampled every 2 min or 10 min. Hence,3000 XMEAS (1)–(4), 1500 XMEAS (5)–(7) and 300 XMEAS (8)–(9) are collected in total. As in the last case, the proposed K-MPPCA, KPPCA1, KPPCA2, and Q-KPCA models are built based on these normal datasets. Similarly, the KPPCA1model only uses the data with the highest sampling rate for modeling. Although the sampling number is as large as the K-MPPCA model, other low sampled variables are not utilized. KPPCA2model only selects the data at the sampling interval when all variables have been recorded, which indicates that only 300 samples are used. The Q-KPCA model uses XMEAS (1)–(4) as process variables and XMEAS (9) as the quality variable. Similar to KPPCA2, only 300 samples which contain all the measurements are used for training. Inthis case, the traditional Gaussian kernel is still selected as the kernel method and the kernel parameter of K-MPPCA is set to be 1000 while the kernel parameters of two KPPCA models and the Q-KPCA model are set to be 800 according to the tuning result. The dimension of all feature spaces of both the K-MPPCA and KPPCA model are set to 20. According to the fluctuation of the raw materials, the DCS database has recorded two types of faults. To measure the effectiveness of fault detection, another 3000 min of process variables were collected as the test data and the faults are started at the 1501st min. The false alarm rate and missing detection rate are used to compare the detection performance of different models.The results for both faults are given in Table IV.

TABLE III PROCESS DESCRIPTION AND SAMPLING RATES OF THE PRE-DECARbURIZED UNIT
It can be found that the fault detection performance of the K-MPPCA model is improved compared with alternatives, as in the last case. For both faults, the abnormal condition can be opportunely detected with the low false alarm rates. In contrast, the false alarm rates of the two types of KPPCA models are much higher, which indicates the control limits of these two models are wrong and the corresponding detection results are invalid. Especially, the missing detection rates ofT2andSPEstatistics in Fault 1 are all close to zero with the normal false alarm rates. However, the detection performance ofthe normal testdatausing KPPCA1andKPPCA2areboth higher so that the correspondingfault detectionresults invalid.The fault detection performance of the Q-KPCA model performs better than KPPCA model due to its functionality with nonlinear models. However, K-MPPCA is still superior since it can deal with the multi-rate modeling problems. The detailed process monitoring result of Fault 1 is shown in Fig. 4.
VI. CONCLUSIONS
In this paper, a kernel generalized MPPCA model has been proposed for nonlinear process modeling and monitoringpurpose. With the introduction of the kernel trick for process variables with different sampling rates, a nonlinear multi-rate probabilistic model is derived to utilize all the measurements from different sampling scales. Also, the corresponding fault detection approach is developed based on the proposed KMPPCA. The case study of numerical example and an actual industrial process example prove the feasibility of the proposed method. In our future studies, more nonlinear modeling technologies like the deep learning models will be explored for multi-rate process monitoring purpose, in which the nonlinear modeling performance for the measurements with different sampling rates are desired to be further improved. At the same time, more complex data characteristics like the auto-correlations will be considered simultaneously.

TABLE IV MONITORING RESULTS IN THE PRE-DECARbONIZATION UNIT

Fig. 4. Monitoring results of Fault 1 in the pre-decarbonization unit by (a) K-MPPCA, (b) KPPCA1, (c) KPPCA2, (d) Q-KPCA.
APPENDIX A DETAIL DERIVATION OF THE M-STEP
As we defined above, the parameters estimation equations are given as follows:



Based on the derivation in (1), the estimation equations for other parameters can be rewritten in a similar way as

In (22), the projection of the process variables can not be directly obtained. Hence, (22) can be rewritten as follow by introducing the kernel matrix. Here we take the equation ofSPE1as the example:
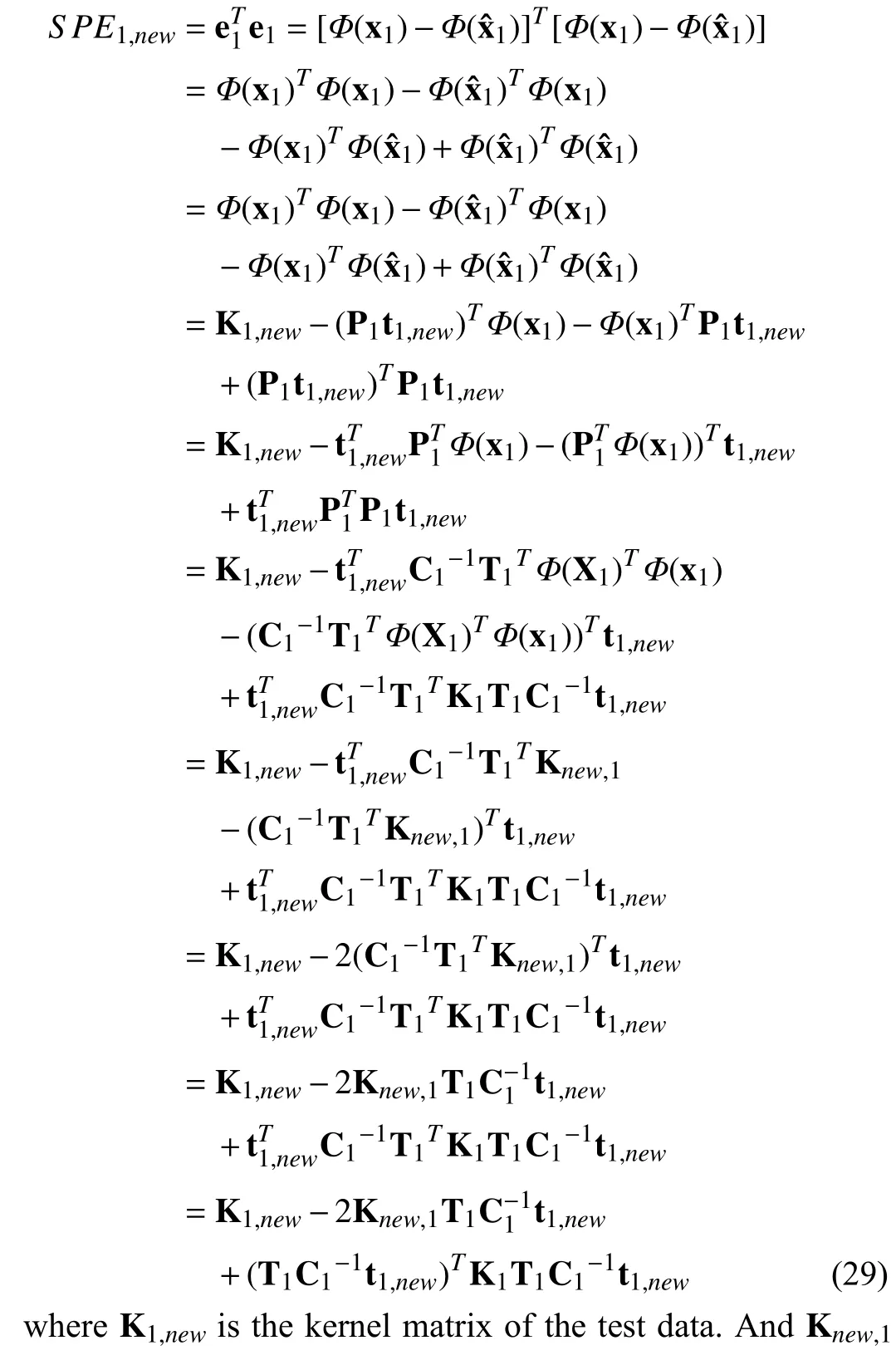

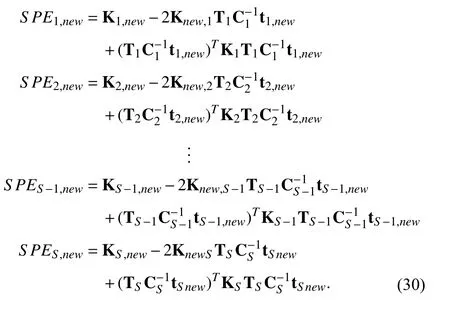
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Distributed Subgradient Algorithm for Multi-Agent Optimization With Dynamic Stepsize
- Learning Convex Optimization Models
- An RGB-D Camera Based Visual Positioning System for Assistive Navigation by a Robotic Navigation Aid
- Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids
- Cooperative Multi-Agent Control for Autonomous Ship Towing Under Environmental Disturbances
- Passivity-Based Robust Control Against Quantified False Data Injection Attacks in Cyber-Physical Systems
