Distributed Subgradient Algorithm for Multi-Agent Optimization With Dynamic Stepsize
2021-07-26XiaoxingRenDeweiLiYugengXiandHaibinShao
Xiaoxing Ren, Dewei Li, Yugeng Xi,, and Haibin Shao,
Abstract—In this paper, we consider distributed convex optimization problems on multi-agent networks. We develop and analyze the distributed gradient method which allows each agent to compute its dynamic stepsize by utilizing the time-varying estimate of the local function value at the global optimal solution.Our approach can be applied to both synchronous and asynchronous communication protocols. Specifically, we propose the distributed subgradient with uncoordinated dynamic stepsizes(DS-UD) algorithm for synchronous protocol and the AsynDGD algorithm for asynchronous protocol. Theoretical analysis shows that the proposed algorithms guarantee that all agents reach a consensus on the solution to the multi-agent optimization problem. Moreover, the proposed approach with dynamic stepsizes eliminates the requirement of diminishing stepsize in existing works. Numerical examples of distributed estimation in sensor networks are provided to illustrate the effectiveness of the proposed approach.
I. INTRODUCTION
DISTRIBUTED optimization in multi-agent systems has received extensive attention due to its ubiquity in scenarios such as power systems [1], [2], smart grids [3], [4],compressed sensing problems [5], [6], learning-based control[7], and machine learning [8], [9], etc. In distributed optimization problems, a whole task can be accomplished cooperatively by a group of agents via simple local information exchange and computation.
There exist various studies of distributed optimization methods based on multi-agent networks. Among them, the most widely studied is distributed gradient methods. In this line of research, Nedic and Ozdaglar [10] develop a general framework for the multi-agent optimization problem over a network, they propose a distributed subgradient method and analyze its convergence properties. They further consider the case where the agent’s states are constrained to convex sets and propose the projected consensus algorithm in [11]. The authors of [12] develop and analyze the dual averaging subgradient method which carries out a projection operation after averaging and descending. In [13], two fast distributed gradient algorithms based on the centralized Nesterov gradient algorithm are proposed. Novel distributed methods that achieve linear rates for strongly convex and smooth problems have been proposed in [14]–[18]. The common idea in these methods to correct the error caused by a fixed stepsize is to construct a correction term using historical information. To deal with the case where communications among agents are asynchronous, some extensions have been proposed. Nedic[19] proposes an asynchronous broadcast-based algorithm while authors in [20] develop a gossip-based random projection (GRP) algorithm, they both study the convergence of the algorithms for a diminishing stepsize and the error bounds for a fixed stepsize. Leiet al. [21] consider the distributed constrained optimization problem in random graphs and develop a distributed primal-dual algorithm that uses the same diminishing stepsize for both the consensus part and the subgradient part.
The selection of stepsize is critical in the design of gradient methods. Typically, the literature considers two types of methods, namely, diminishing stepsizes and fixed stepsizes.The existing distributed gradient methods with diminishing stepsizes asymptotically converge to the optimal solution. The diminishing stepsizes should follow a decaying rule such as being positive, vanishing, non-summable but square summable, see e.g., [10], [11], [13], [19]–[22]. While in [23],a wider selection of stepsizes is explored, the square summable requirement of the stepsizes commonly adopted in the literature is removed, which provides the possibility for better convergence rate. These methods are widely applicable to nonsmooth convex functions but the convergence is rather slow due to diminishing stepsizes. With a fixed stepsize, it is shown in [24] that the algorithm converges faster but only to a point in the neighborhood of an optimal solution. The recent developed distributed algorithms with fixed stepsizes[14]–[18] achieve linear convergence to the optimal solution.However, it requires that the local objective functions are strongly convex and smooth. Besides, the fixed stepsize should be less than a certain critical value which is determined by the weighted matrix of the network, the Lipschitz continuous and the strongly convex parameters of the objective functions. Thus, these algorithms have restricted conditions on the fixed stepsize and require the knowledge of global information, which makes it not widely applicable.
By comparison to the previous work, the contribution of this paper is a novel dynamic stepsize selection approach for the distributed gradient algorithm. We develop the associated distributed gradient algorithms for synchronous and asynchronous gossip-like communication protocol. An interesting feature of the dynamic stepsize is that differently from the existing distributed algorithms whose diminishing or fixed stepsizes are determined before the algorithm is run, the proposed distributed subgradient with uncoordinated dynamic stepsizes (DS-UD) and AsynDGD algorithms use dynamic stepsizes that rely on the time-varying estimates of the optimal function values generated at each iteration during the algorithm. The advantages of this dynamic stepsize proposed in this paper lie in two aspects. On the one hand, the dynamic stepsize only requires that the local convex objective functions have locally bounded subgradients for the synchronous scenario and have locally Lipschitz continuous bounded gradients for the asynchronous scenario. Besides, the dynamic stepsize needs no knowledge of the global information on the network or the objective functions. Thus, the proposed algorithms are more applicable compared with the distributed algorithms with fixed stepsize. On the other hand, the dynamic stepsize can overcome inefficient computations caused by the diminishing stepsize and achieve faster convergence. The dynamic stepsize is a generalization of the Polyak stepsize [25], which is commonly used in centralized optimization and is shown to have faster convergence than the diminishing stepsize even with the estimated optimal function value [26]. Note that the proposed algorithms utilize two gradients at each iteration: one of them is used to construct the stepsize, and the other one is for the direction, which means that the iteration complexity of the algorithm is doubled.However, numerical examples in which the plots are in terms of the number of gradient calculations illustrate the effectiveness of the proposed algorithms.
The remainder of this paper is organized as follows. In Section II, we describe the problem formulation. The distributed subgradient algorithm with uncoordinated dynamic stepsize and the convergence analysis are provided in Section III. Section IV discusses the extension of the proposed algorithm to the asynchronous communication protocol. In Section V, we apply our algorithms to distributed estimate problems to illustrate their effectiveness. Finally, we make concluding remarks in Section VI.


II. PRObLEM FORMULATION
Consider a network consisting ofNagents, the goal of the agents is to solve the following problem defined on the network cooperatively


III. DISTRIbUTED SUbGRADIENT ALGORITHM WITH DYNAMIC STEPSIZES
In this section, we derive the distributed subgradient algorithm with dynamic stepsizes for synchronous communication protocol and present its convergence analysis.
A. Algorithm Development

Algorithm 1 summarizes the above steps, this distributed subgradient method with uncoordinated dynamic stepsizes is abbreviated as DS-UD.
Remark 1:Since the convergence speed of the algorithm varies when solving different specific optimization problems,different maximum iteration numbers can be set for different problems to ensure that the optimality error decreases rather slowly at the maximum iteration. In practical applications, we can set the maximum iteration number according to the connectivity of the multi-agent network and the scale of the optimization problem.

Algorithm 1 DS-UD xi0=yi0 ∈Ω ∀i ∈V W ∈RN×N k=0 1: Initial: Given initial variables , , the weight matrix under Assumptions 2 and 3, and the maximum iteration number. Set .2: Obtain the estimate: For , each agent computes (2) and(3) to get the estimate .i ∈V i fest i (k)3: Dynamic stepsize: Each agent obtains its stepsize based on the estimate according to (4) and (5).i k=k+1 i αi,k fest i (k)4: Local variable updates: Each agent updates according to (6).Set .5: Repeat steps from 2 to 4 until the predefined maximum iteration number is reached.
B. Analysis of the Algorithm

Substitute (9) into (8), for allx∈Ω andk≥0,




IV. ASYNCHRONOUS COMMUNICATION
In this section, we extend the DS-UD algorithm to the asynchronous communication protocol, which allows a group of agents to update while the others do not in each iteration.Also, we establish the convergence analysis of the proposed asynchronous algorithm.
A. Algorithm Development
In practical multi-agent systems, there exist uncertainties in communication networks, such as packet drops and link failures. We consider the gossip-like asynchronous communication protocol from [28]. Specifically, each agent is assumed to have a local clock that ticks at a Poisson rate of 1 and is independent of the other agent’s clocks. This setting is equivalent to having a single virtual clock whose ticking times form a Poisson process of rateNand which ticks whenever any local clock ticks. LetZkbe the absolute time of thek-th

The idle agents do not update, i.e.,

This asynchronous distributed gradient method with dynamic stepsize is abbreviated as AsynDGD, Algorithm 2 summarizes the above steps. We would like to remark that the maximum iteration number in Algorithm 2 is set in the same way as Algorithm 1.

Algorithm 2 AsynDGD xi0=yi 0 ∈Ω ∀i ∈V 1: Initial: Given initial variables , and the maximum iteration number. Set .i ∈V i ∈Jk i ∉Jk k=0 2: Asynchronous updates: For , if , go to Step 3, if ,go to Step 6.3: Optimal value estimation: Agent computes (20) and (21) to get the estimate .i fest i (k)4: Dynamic stepsize: Agent calculates its stepsize based on the estimate according to (22) and (23).i k=k+1 i αi,k fest i (k)5: Local variable updates: Agent updates according to (24). Set, go to Step 7.i k=k+1 6: Idle agent does not update and maintain its variables in the new iteration as (25) and (26). Set .7: Repeat steps from 2 to 6 until the predefined maximum iteration number is satisfied.
B. Analysis of the Algorithm
To define the history of the algorithm, we denote the σalgebra generated by the entire history of our algorithm until timekbyFk, i.e., fork≥0,
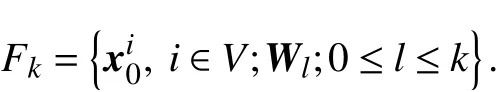






The convergence rates of the distributed gradient algorithms[11], [20] to the optimal solution are sublinear for convex functions due to the use of diminishing stepsize. The convergence rates of DS-UD and AsynDGD are also sublinear, however, we will discuss in detail why the proposed algorithms can achieve faster convergence than the algorithms with diminishing stepsizes.
Recall that the dynamic stepsize is defined by


V. NUMERICAL EXAMPLES
In this section, we provide numerical examples on the convergence performance of the proposed algorithms and provide comparisons with the existing distributed gradient algorithms. The results are consistent with our theoretical convergence analysis and illustrate the improved algorithmic performance.
Example 1:First, we study the performance of DS-UD. We consider an undirected cycle consisting of 4 agents. The convex objective functions are as follows.



Fig. 1. The estimates of 4 agents and the residual of the DS-UD algorithm.(a) The estimates for the first component. (b) The estimates for the second component. (c) The residual.

where γiis the regularization parameter.
Consider a randomly generated undirected connected network consisting of 100 sensors, the average degree of the network is 49. We sets=10,d=10 and γi=0.05. The symmetric measurement matrixMi∈R10×10has eigenvalues


Fig. 2. The normalized relative errors of three algorithms. (a) The normalized relative errors of DGD, D-NG and DS-UD algorithms versus the number of iterations. (b) The normalized relative errors of DGD, D-NG and DS-UD algorithms versus the number of gradient calculations.
Note, that the proposed DS-UD algorithm utilizes two gradients at each iteration: one of them is used to construct the stepsize, and the other one is for the update direction. This means that the iteration complexity (number of gradients calculations at each iteration) of the DS-UD algorithm is twice as those of the DGD, D-NG and DDA algorithms. Therefore,to have a fair comparison with the DGD, D-NG and DDA algorithms, the plots in Fig. 2(a), Fig. 3(a) are in terms of the number of iterations and the plots in Fig. 2(b), Fig. 3(b) are in terms of the number of gradient calculations.

Fig. 3. The normalized relative errors of three algorithms. (a) The normalized relative errors of DGD, DDA and DS-UD algorithms versus the number of iterations. (b) The normalized relative errors of DGD, DDA and DS-UD algorithms versus the number of gradient calculations.

Moreover, DS-UD requires fewer iterations and gradient calculations to solve the optimization problem to a high-level of accuracy than the DGD, D-NG and DDA algorithms. It can be seen that DS-UD brings a satisfactory convergence result for the distributed optimization problem and outperforms the DGD, D-NG and DDA algorithms.
Besides, we provide the trajectory of dynamic stepsizes in DS-UD and compare it to the diminishing stepsize in DGD.


Fig. 4. The stepsizes of DGD and DS-UD algorithms.
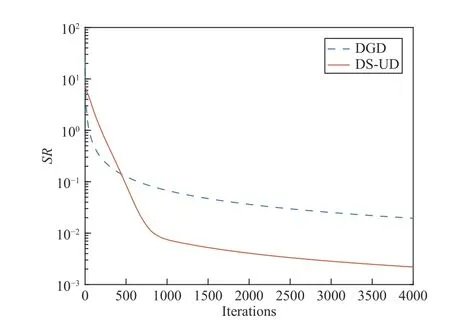
Fig. 5. The distance S R between the current stepsizes and the optimal stepsizes of DS-UD and DGD algorithms.

Example 3:Now, we examine the effectiveness of AsynDGD. We compare it with the GRP algorithm in [20]and the primal-dual algorithm in [21].
Consider an undirected fully connected network consisting of 10 sensors. The sensors are attempting to measure a parameter θˆ by solving the distributed estimation problem(46). We sets=1,d=2, γi=0.2.Mi∈R1×2has entries randomly generated in (0,1) and the noise ωi∈R follows an i.i.d.Gaussianse{quenceN(0,0}.1),i=1,...,10. The constraintsetisΩ=θ∈R2:‖θ‖≤5.
In the asynchronous scenario, for fair comparison, the three algorithms are assumed to use the same gossip-like protocol as in this work. Specifically, at each iteration, one of the 10 sensors will be randomly selected to be idle, it does not update and the associated edges are not activated.

Fig. 6(a) depicts the averaged normalized relative error(over the Monte-Carlo runs) of the three algorithms versus the total number of iterations. Fig. 6(b) depicts the averaged normalized relative error (over the Monte-Carlo runs) of the three algorithms versus the total number of gradient calculations of 10 sensors. Fig. 6 shows that GRP and the primal-dual algorithm converge faster than AsynDGD at the beginning, but fall behind AsynDGD after short fast convergence. Besides, AsynDGD requires fewer iterations and gradient calculations to solve the optimization problem to a high-level of accuracy than GRP and the primal-dual algorithm. The reason for the observed result is the same as that in Example 2 and thus is omitted. It is seen that AsynDGD achieves improved convergence performance for the distributed optimization problem.
VI. CONCLUSIONS
In this paper, distributed gradient algorithms with dynamic stepsize are proposed for constrained distributed convex optimization problems. First, we develop distributed optimization algorithms for both synchronous and asynchronous communication protocols, in which each agent calculates its dynamic stepsizes based on the time-varying estimates of its local function value at the global optimal solution. Second, we present the convergence analysis for the proposed algorithms. Besides, we compare them with the existing algorithms through numerical examples of distributed estimation problems to illustrate their effectiveness.

Fig. 6. The averaged normalized relative errors of three asynchronous algorithms. (a) The averaged normalized relative error of there asynchronous algorithms versus the number of iterations. (b) The averaged normalized relative error of there asynchronous algorithms versus the number of gradient calculations.
杂志排行
IEEE/CAA Journal of Automatica Sinica的其它文章
- Kernel Generalization of Multi-Rate Probabilistic Principal Component Analysis for Fault Detection in Nonlinear Process
- Learning Convex Optimization Models
- An RGB-D Camera Based Visual Positioning System for Assistive Navigation by a Robotic Navigation Aid
- Robust Controller Synthesis and Analysis in Inverter-Dominant Droop-Controlled Islanded Microgrids
- Cooperative Multi-Agent Control for Autonomous Ship Towing Under Environmental Disturbances
- Passivity-Based Robust Control Against Quantified False Data Injection Attacks in Cyber-Physical Systems
