动态载荷下铁相变的原子模拟研究进展

王 昆，肖时芳，祝文军，陈 军，胡望宇

（1. 湖南大学材料科学与工程学院，湖南 长沙 410082；2. 湖南大学物理与微电子科学学院，湖南 长沙 410082；3. 中国工程物理研究院流体物理研究所冲击波物理与爆轰物理重点实验室，四川 绵阳 621999；4. 北京应用物理与计算数学研究所，北京 100088）

绝大多数元素及其化合物在高压下会发生多型相变，并且以马氏体相变为主。在自然界和人类生产生活中的很多场景都存在高压条件，如地心的极端高压环境、陨石撞击事件、车辆碰撞、金属材料的冲压塑性成型等。探测铁的高压多型相变有助于正确认识地心的多层结构[1–2]。金属材料的多型相变/逆相变会改变材料的性质、塑性机制耦合、促进或抑制额外晶体缺陷的产生等，进而影响材料的断裂及屈服行为[3–5]。铁的 α↔ε相变[6–7]是金属高压多型相变的典型范例，迄今为止，相关研究已持续近70 年，在实验测试和机理分析方面取得了丰硕的成果。2000 年之前，相关研究主要以实验与宏观理论分析为主，在这方面已有不少经典综述和专著报道[8–11]。随着计算机技术的快速发展和原子尺度模拟方法的逐步推广应用，铁的冲击相变研究逐步深入到微观原子尺度，特别是原位在线诊断实验技术的突破，极大地促进了该领域的蓬勃发展。近20 年铁高压相变的原子模拟研究可大致分为两个阶段：2011 年及以前是以Voter-Chen 势为基础的分子动力学（Molecular dynamics，MD）模拟研究，主要探讨铁的冲击相变机制、相变产物类型以及相变形核与生长规律，这部分进展将在本文第1 节的开始部分进行简要回顾；第2 阶段是以改进的铁原子间相互作用势为基础的MD 模拟，主要探讨相变的变体选择规则、相变与塑性、相变与层裂等问题，本文将重点梳理这一阶段的研究进展。

在热力学方面，高压相变理论研究主要关注压力对晶体结构稳定性的影响（如高压相图）；而在动力学方面，则主要关注压力等因素对相转变过程的影响（如相转变路径、相变成核条件、相变与塑性的相互作用等）[10]。前者从热力学原理探索潜在新相存在的可能性，后者则针对实际相转变过程，探讨新相形核与长大的条件。两者相辅相成，相变动力学研究不能脱离平衡相图的约束，而平衡相图的实验研究也离不开相变动力学，例如：实验中观察到的相变-逆相变压力回滞现象就是受相变动力学的影响[12]。目前，晶体高压平衡相变的理论预测通常采用密度泛函理论结合适当的晶体结构搜索算法来完成，国际上已有大量的研究工作，尤其是AIRSS[13]、CALYPSO[14]、IM2ODE[15]等晶体结构预测软件的出现，使晶体材料高压结构相变的理论预测工作变得程式化。相变动力学研究主要依赖于实验与大规模经典MD 模拟，尤其是激光加载结合原位飞秒X 射线衍射测量技术的出现[16]，使人们能够直接观测金属在晶格尺度的动力学过程，结合MD 模拟结果，有望在晶格层次揭示整个动态响应过程及其物理本质，为高压相变动力学物理建模提供可靠的理论支撑。

本文主要以铁的 α↔ε相变为例，综述MD 模拟在相变动力学方面的研究进展。首先介绍经典MD 模拟研究所采用的铁高压相变的原子间相互作用势函数，重点讨论平面应变加载下铁的相变机制及动力学的影响因素，包括加载强度、晶体各向异性、应变率、应变梯度、初始微结构等，然后简要介绍 工程实际中的特殊加载对相变的影响，最后进行总结和展望。

1 铁的原子间相互作用势函数

随着压强的增大，铁 α相的吉布斯自由能（Gα）逐渐接近甚至高于 ε 相的吉布斯自由能（Gε），在相变压力阈值（pc）处两者相等。由图1 所示的铁的相图可知， α 与 ε 相边界较陡，即pc受温度的影响小。在零级近似下，令温度为零，相变的热力学条件实际上要求两相的焓相等，即

图1 铁的高压相图[17]Fig. 1 High-pressure phase diagram of iron[17]

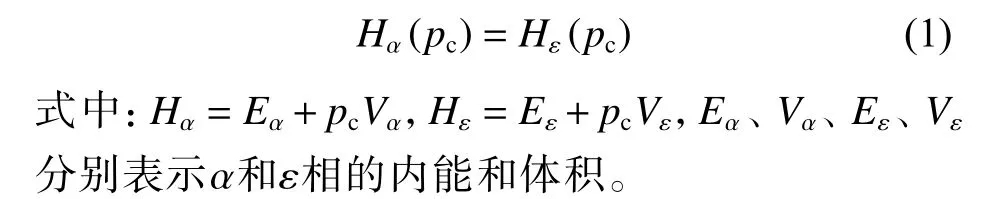
在MD 模拟中，能否正确描述铁的 α↔ε相变完全取决于所采用的原子间相互作用势函数。由于大规模非平衡分子动力学（Non-equilibrium molecular dynamics，NEMD）模拟对计算效率的要求很高，金属体系的势函数通常采用嵌入原子模型（Embedded atom model，EAM）势或Finnis-Sinclair（FS）势，因此本文的讨论仅限于这两种类型的势及相关研究工作。大约在2000 年以前，国际上绝大多数势函数是针对常压应用环境开发的，主要探讨金属在常压下的热力学行为，以扩散机制为主。将这些势函数直接应用于高压下金属力学行为的模拟时，常常会遇到一些与实验观测不相符的现象。铁是其中最典型的例子。2012 年以前国际上常用的铁的势函数主要有3 种：Voter-Chen 势[18]、Meyer-Ente 势[19]和Mendelev 势[20]。由式(1)检验发现[21–22]，只有Voter-Chen 势可以同时正确描述铁的bcc（体心立方， α相）↔hcp（密排六方， ε相）及其相变压力阈值。然而，NEMD 模拟研究发现，Voter-Chen 势只能正确描述[001]晶向的冲击相变产物，其他晶向的冲击相变产物主要为fcc（面心立方）相。尽管如此，基于Voter-Chen 势的原子模拟研究在历史上发挥了巨大的作用。例如，人们曾一度认为fcc 相是铁 α↔ε相变的中间产物[23–24]，即所谓的“三步转变”机制，之后Hawreliak 等[25]结合冲击波实验和大规模NEMD 模拟方法排除了这种相变机制，基于密度泛函理论的计算分析同样排除了fcc 相出现的可能性[26]。现在公认的铁的相变机制[22,27–28]如图2所示，即沿 α铁的[001]晶向压缩15%～18%，然后通过相邻(110)面间的穿插，最终形成ε 相。受实际样品尺寸的限制，在相变的第一步压缩过程中可能出现一个额外的沿(110)[111]方向的微小剪切变形，使最终的变体绕c轴转动了约5°[29]。对于大规模NEMD 模拟而言，由于在垂直冲击波传播方向一般采用周期性边界条件，所以这种额外的小转动不太明显。

此外，无论是单晶还是多晶，Voter-Chen 势的模拟结果都没有观察到位错[22,30]，这与实验不符。因此，要深入开展铁的高压相变动力学研究，必须发展新的原子间相互作用势函数。如何构建能够正确描述高压相变现象的原子间相互作用势函数是原子尺度模拟材料动态相变行为的一个亟待解决的重要应用基础科学问题，与之密切相关的还有冲击塑性（如孪晶、位错等）的原子模拟问题。最近10 年，针对高压应用环境，国内外在发展高压原子间相互作用势函数方面已经进行了一些重要的探索，除了本文将要介绍的铁的势函数以外，还有描述冲击高压下钽形变孪晶的势函数[31]、钨位错芯结构与形变孪晶的势函数[32]、铅塑性与相变的势函数[33]等。本节将介绍2012 年以后铁高压势函数研究的最新进展，主要包括两种势，即改进的Ackland 势[21]和改进分析型嵌入原子模型势（MAEAM）[34]，通过对比分析不同原子间相互作用势的特点，总结出能够模拟高压相变与塑性行为的势函数应具备的最基本特征，为将来进一步改进或发展其他元素的高压势函数提供解决思路。

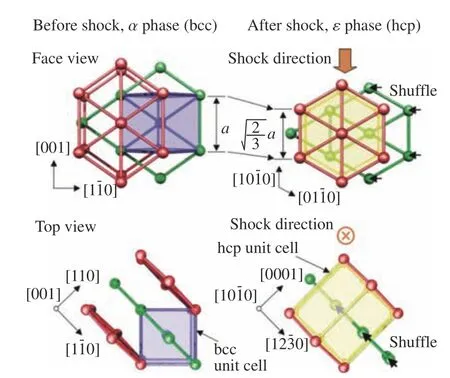
图2 单晶铁沿[001]晶向冲击的相变机制[27]Fig. 2 Phase transition mechanism of single crystalline iron under the shock along [001] direction[27]

1.1 改进的Ackland 势

式中：f(rij)为原子电子密度。式（2）与式（3）中的求和遍及体系中所有原子，具体形式如下

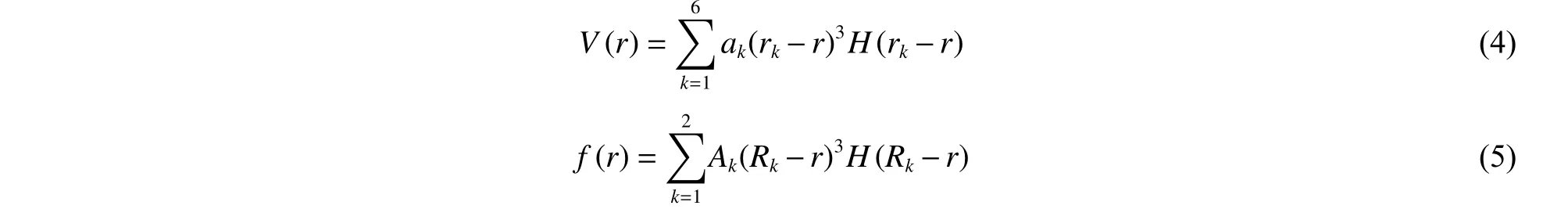
式中：H(x)为阶跃函数。模型中的势参数见表1[36]。

表1 改进的Ackland 势参数[36]Table 1 Parameters of modified Ackland potential[36]

1.2 MAEAM 势

我国在铁的高压原子间相互作用势函数研究方面与国外几乎同时起步，湖南大学胡望宇课题组与中国工程物理研究院流体物理研究所祝文军团队合作，在MAEAM 模型势框架下[37]发展了一个可以同时正确描述铁冲击相变与塑性的势函数[34,38]。在该模型框架下，第i个原子的能量等于两体相互作用能（V）、嵌入能（F）与能量修正项（M）之和

嵌入能F(ρi)表示为电子密度 ρi的函数

其中

式中：Pe为平衡态下的电子密度偏离函数值。针对铁的高压应用环境，优化的势模型参数见表2[34]。

表2 MAEAM 势参数[34]Table 2 Parameters of MAEAM potential[34]

1.3 高压势函数的验证与评价

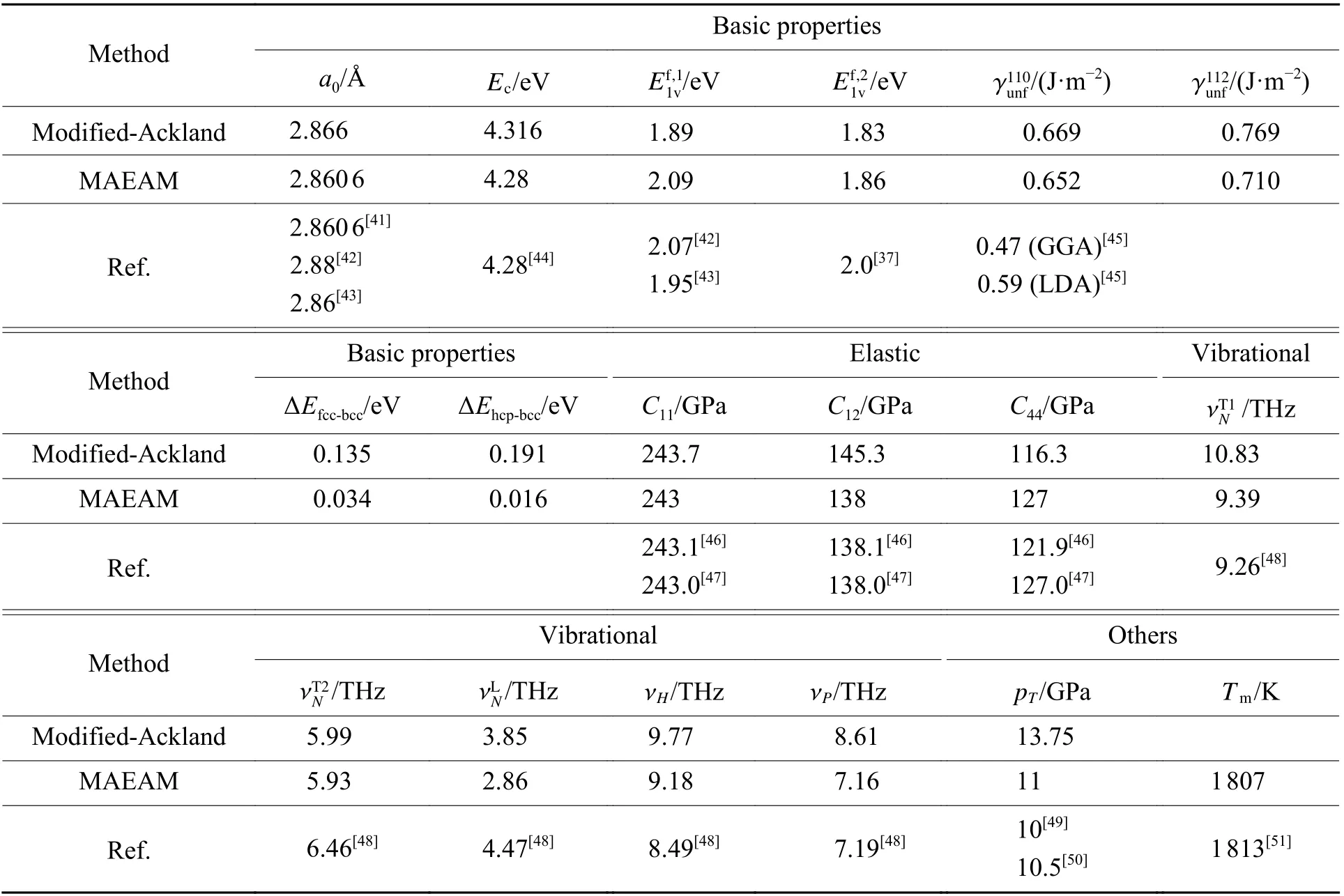
表3 改进的Ackland 势与MAEAM 势预测的铁主要物理性质与有关第一原理计算及实验结果的对比Table 3 Comparisons of key properties of iron predicted using modified Ackland potential and MAEAM potential with the first-principle-base calculations or experimental results

满足表3 中的基本物性可以保证势函数正确描述平衡态附近的基本热力学行为和高压结构相变，要正确模拟铁的冲击雨贡纽关系，还需要验证高压物态方程。图3(a)为MAEAM 势预测的铁的3 种相的物态方程与有关实验及第一原理计算结果的对比，可见MAEAM 势可以很好地重现实验高压状态方程直到200 GPa 以上。改进的Ackland 势的预测结果见图3(b)，其预测的高压相的物态方程偏硬。

图3 (a) MAEAM 势预测的物态方程与实验及第一原理计算结果的对比，(b) 采用MAEAM 势与改进的Ackland 势的计算结果对比[49,52–54]Fig. 3 (a) Comparison of equations of states predicted by MAEAM potential with experiments and the first-principle calculations,(b) Comparison of the results between MAEAM potential and modified Ackland potential[49,52–54]

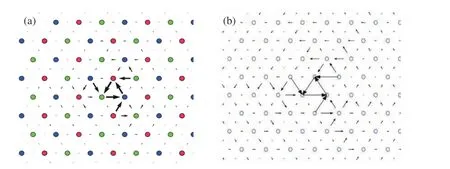
图4 MAEAM 势(a)和改进Ackland 势(b)预测的简并<111>/2 螺位错芯结构[21]Fig. 4 Degenerate core structure of <111>/2 screw dislocations predicted by (a) MAEAM and (b) modified Ackland potential[21]

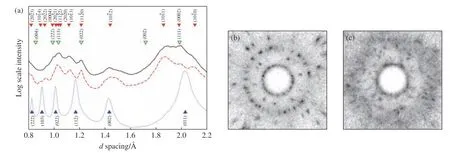
图5 弹性压缩和相变的截面轮廓(a)，模拟的未冲击样品(b)和相变后样品(c)的实验衍射图样[36]Fig. 5 Line profile from elastically compressed and phase changed sections of samples (a), and the simulated diffraction patterns in an experimental geometry: (b) unshocked and (c) phase-changed sample[36]

2 平面加载下的结构相变

利用原子模拟方法在材料中实现高应变率变形主要有3 种途径（见图6）：第1 种是用一个“刚性”的活塞（飞片）从左侧撞击靶材料，在靶材料中产生一个向右传播的冲击波；第2 种是两个靶碰撞，在两个靶中分别产生向相反方向运动的冲击波；第3 种是沿加载方向以一定的应变率均匀单轴压缩材料，该加载方式不会在材料中形成冲击波，便于分析材料力学行为机理的控制因素。通过第3 种途径模拟的样品相当于斜波压缩样品中的一个拉格朗日单元，在一些文献[55]中也将该途径等同于斜波（或“准等熵”）加载。采用这些模拟技术结合第1 节提到的铁的高压势函数，近10 年在铁的高压相变机制、相变对织构的影响、相变形核阈值、生长规律以及相变与塑性的微观耦合机制等诸多方面取得了大量突破性认识，呈现出包括材料物理、冶金、固体力学、冲击动力学等多学科交叉融合的特点。

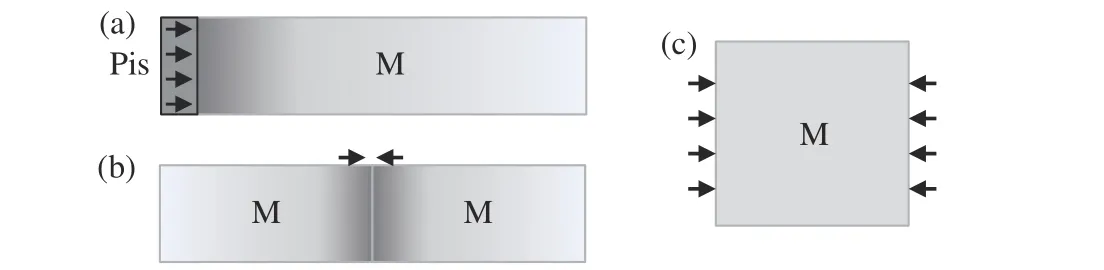
图6 实现高应变率加卸载的3 种方法：(a)活塞加载，(b)对称撞击，(c)均匀单轴压缩（“M”表示材料，箭头表示活塞或材料的运动方向，灰色梯度表示材料受到碰撞时形成的冲击波）Fig. 6 Three simulation approaches of de-/compression under high strain rates: (a) piston loadings, (b) symmetric impingements and(c) uniform uniaxial compressions, where “M” represents materials and the arrows show the motion directions of the piston and materials, and shock waves initiated around the impinging moment are illustrated by the grayscale

2.1 加载强度与晶体各向异性

图7 单晶铁的冲击雨贡纽关系[34]Fig. 7 Shock Hugoniot relation of single crystalline iron[34]

用MAEAM 势模拟的单晶铁沿不同晶向的冲击雨贡纽关系如图7 所示（其中 σzz为应力的zz分量，v为粒子速度），结果表明沿不同晶向冲击时会出现不同程度的过压，沿[001]、[110]和[111]冲击的平均相变压力阈值分别为18.0、22.3 和23.8 GPa。为了与第1 节的平衡相变相关概念进行区分，本文用相变压力阈值表示实际相变成核的起始压力，用平衡相变压力阈值表示平衡态的转变压力。根据第1 节的讨论可知，bcc→fcc 的平衡相变压力阈值高于[001]晶向的过压均值，略低于[110]和[111]晶向的过压均值，因此用该势模拟两个晶向的冲击相变时，相变产物中会出现少量的fcc 相（如图8(a)所示），但是仍以hcp 相为主，尤其在冲击强度接近相变阈值附近。尽管单晶铁的相变机制在晶体学上已经清楚（见图2），但是由于冲击加载使晶体发生了单轴变形，破坏了bcc 铁原有的立方晶系对称性，即原来等价的晶面或晶向相对于冲击方向变得不等价。由此可知，在相同的相变晶体学机制下，不同的冲击晶向将导致不同的相变路径，产生不同的相变变体，得到不同的产物织构，最终影响晶体塑性行为。图8(b)给出了沿单晶铁3 个低指数晶向冲击的相变产物类型，用hcp 相的基面（惯习面）表征。沿[001]和[111]冲击时，最终的变体类型分别为2 种和3 种，相变后的样品为多晶，与实验观测的单晶冲击结果[27]一致。然而，沿[110]晶向冲击时，变体类型只有一种，相变后的样品仍为单晶，只是其中含有小角度晶界，与相变前的塑性有关[34]。最近的激光加载实验也观察到了这种单一变体的结果[56]。采用改进的Ackland 势和斜波压缩技术，Amadou 等[57]观察到了单晶铁相变前的形变孪晶，并且随着冲击强度的增大或冲击波的形成，形变孪晶的体积分数逐渐减小直至消失，这种现象被认为与高冲击强度下滑移主导的塑性有关。

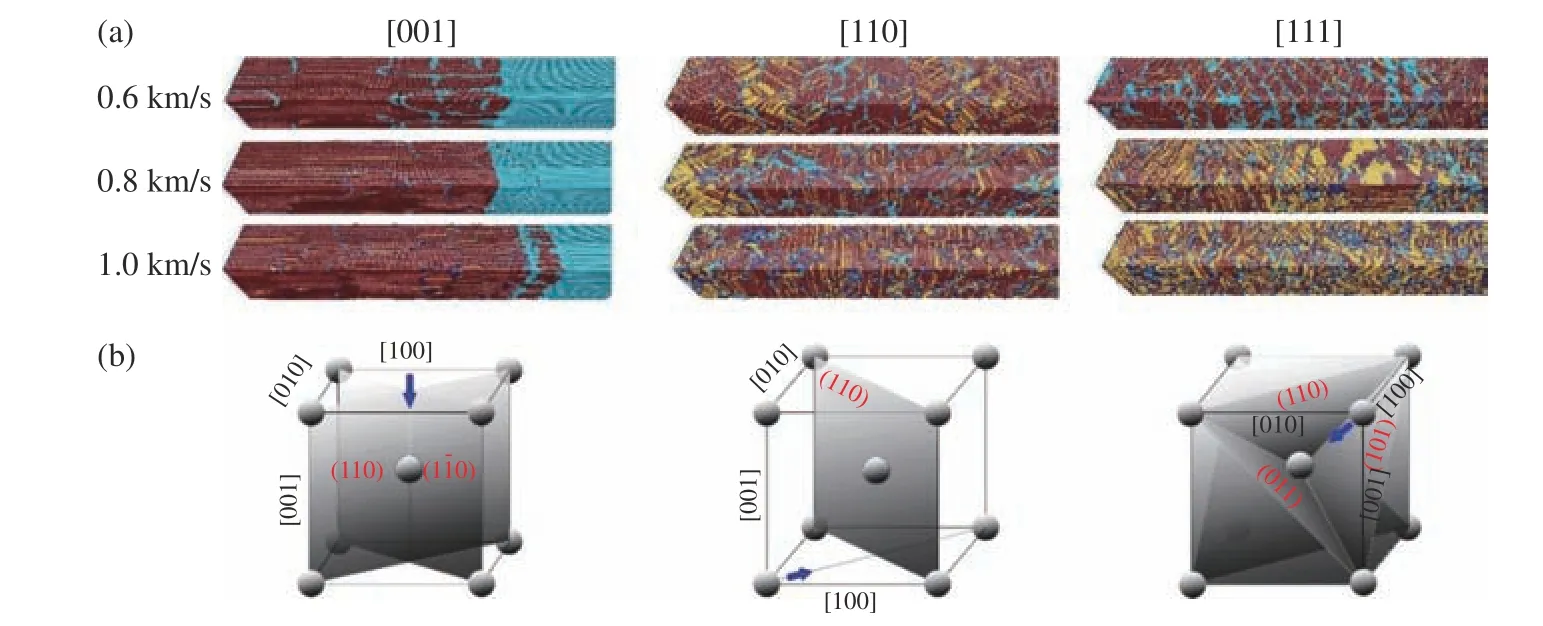
图8 (a)不同冲击晶向与冲击强度下单晶铁的相变（红色、黄色、浅蓝色和深蓝色分别表示hcp 原子、fcc 原子、bcc 原子和缺陷原子），(b)冲击晶向与惯习面的关系[34]Fig. 8 (a) Phase transition of single crystalline iron under different shock directions and shock strength(The meaning of the colors is: red (hcp atoms), yellow (fcc atoms), light blue (bcc atoms) and dark blue (defects).); (b) relationship between the shock direction and habit plane[34]

2.2 应变率与应变梯度效应

2.2.1 应变率效应

激光驱动的斜波压缩实验表明[58]，铁的相变压力阈值（σα→ε）随应变率（ ε˙）的变化规律用如下分段函数拟合

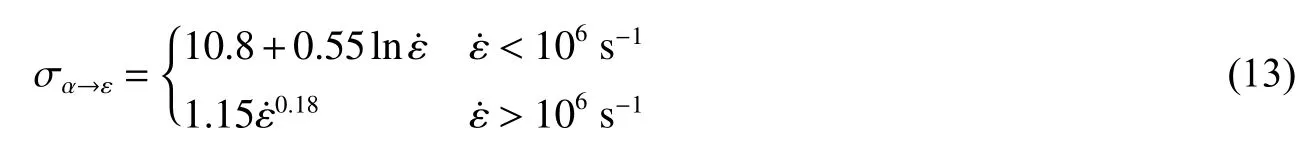
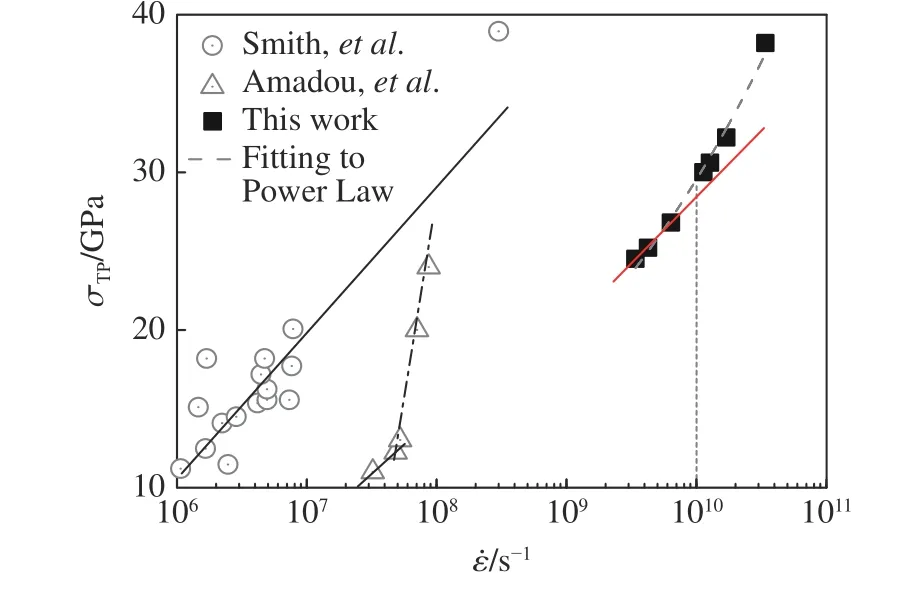
图9 铁的相变压力阈值随加载应变率的变化[61]Fig. 9 Transition pressure of iron as a function of uniaxial strain rate[61]

这种规律类似于屈服强度与应变率的关系[59–60]，因此σα→ε的变化趋势在106s−1附近发生改变的机制也被认为与塑性屈服机制类似，即与热激活的位错运动到声子拖拽机制的转变相关。最近的斜波压缩实验中，通过相变平台弛豫时间随应变率的升高而缩短的现象，推测出相变成核与生长速率均增加[61]。采用NEMD 方法模拟单晶铁在斜波压缩下的相变时发现[62]，相变压力阈值在应变率低于1010s−1时表现出的规律（见图9）与式(13)描述的第2 段规律（即幂次律）类似，然而当应变率高于1010s−1时，相变压力阈值随应变率的变化规律逐渐偏离幂次律。这是因为在极端应变率的斜波压缩下，波前存在很大的应变梯度，例如沿[001]晶向斜波压缩单晶铁的相变，波前应变梯度高达106m−1，使得耦合的应变梯度效应无法忽略。

沿[001]晶向斜波压缩单晶铁的研究结果表明[62]，相变的发生分为弹性单轴压缩导致的晶格失稳、形核与生长直至完全相变几个阶段。随着冲击波的传播，可以发现失稳点与形核点的位置逐渐接近，直到重合，这与形核过程的超声速传播有关[63]。在相变点附近，新相形核初期呈椭球状，其中短轴沿某个(110)面法向，如图10 所示。新相的生长分别通过沿(110)面内的<110>晶向滑移和沿短轴方向相变进行，其滑移方向的生长速度比短轴方向的相变速度快[64]。

尽管斜波加载可以避免冲击加载引起的巨大温升效应，但它仍属于动态加载手段，除了在固体中产生一定的应变率外，还会形成一定的宏观应变梯度。因此，检验应变梯度的影响显得尤为重要。在原子模拟中，采用均匀单轴压缩技术（见图6(c)）不仅可以模拟斜波加载过程中产生的应变率效应，还能排除宏观应变梯度效应的干扰。利用这种技术，邵建立等[65]研究了应变率分别为1.25 × 109和9.1 × 108s−1下相变的形核与生长，观察到了柱状晶粒与层状结构的形成（见图11），与Pang 等[63]在冲击条件下观察到的椭球状晶粒的形核与生长不同。考虑到两种结果都基于Voter-Chen 势，为此推测出现这种差异的原因与应变率相关。Pang 等[63]发现晶粒的形核与生长主要发生在冲击波前沿扫过之后的区域，该区域的宏观应力和应变的变化很小，对应的应变率非常低。

基于MAEAM 势模拟准等熵压缩下单晶铁相变的研究结果表明[62]：当应变率小于或等于109s−1时，临界应变几乎不变；而当应变率高于109s−1时，临界应变快速增大。这主要是因为相变形核需要一定的孕育时间，当应变率较小时，孕育时间可以忽略，当应变率非常大，以至于在极短的孕育时间内材料仍会被进一步压缩至更高的应力状态才发生相变。然而，在斜波压缩下，临界应变随应变率增加到一定程度后反而减小，说明极端应变率下应变梯度对相变形核有重要影响。

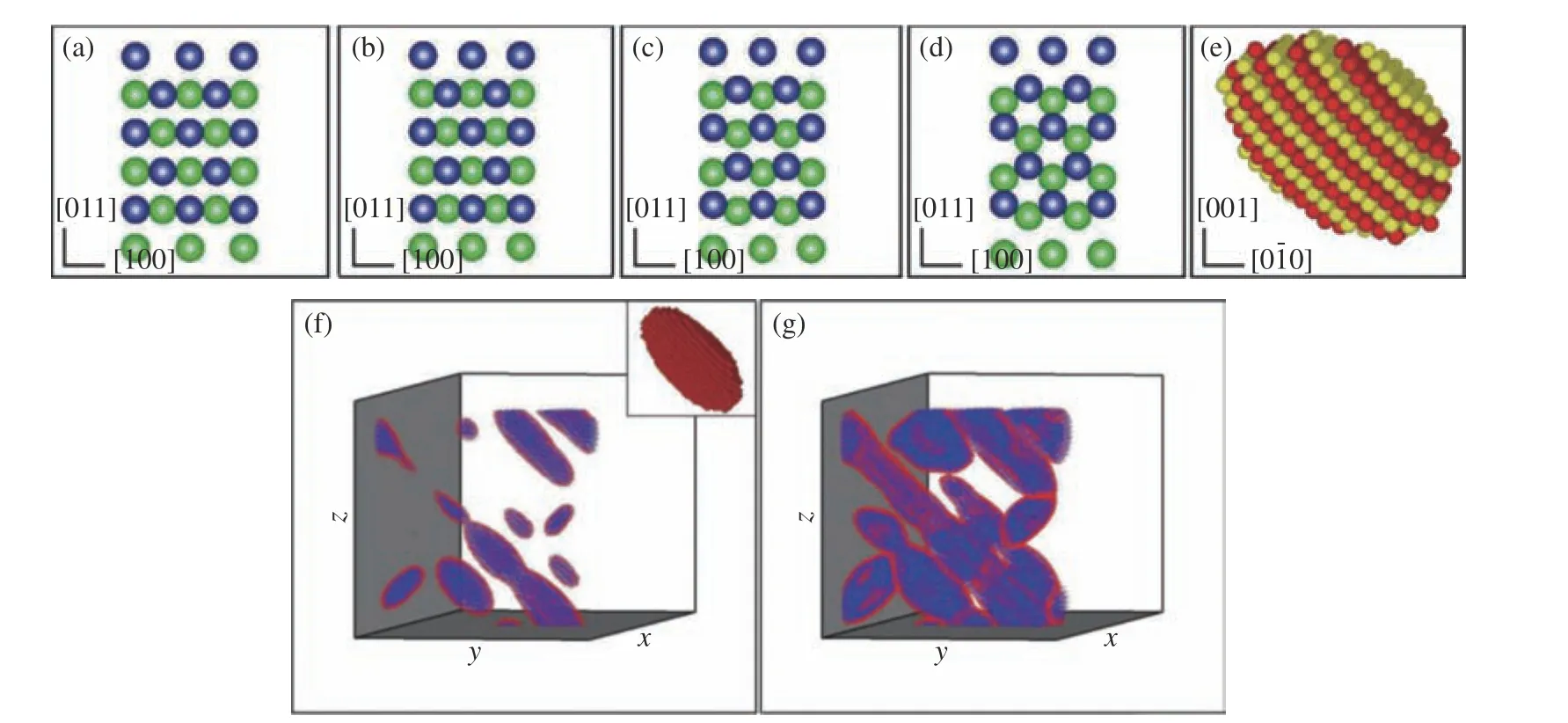
图10 冲击下铁相变的微结构演化：(a)～(e)显示相变机制，(f)～(g)显示新相生长[63]Fig. 10 Microstructure evolutions during the process of shock-induced phase transition of iron:(a)–(e) phase transition mechanism, (f)–(g) growth of the new phase[63]

图11 在应变率为1.25 × 109 s–1 的单轴均匀压缩下hcp 相的形核与生长[65]Fig. 11 Nucleation and growth of hcp phase under unform uniaxial compressions with a strain rate of 1.25 × 109 s–1[65]

2.2.2 基于连续介质假设的应变-应变梯度耦合模型

位移的二阶梯度与应变梯度分别定义为

其中，位移满足uk=xk−Xk。由于应变梯度的出现，晶体中的质量密度（或比体积）将变得不均匀，因此与材料物性相关的密度除了依赖空间位置之外，还依赖计算密度所采用的体积，在梯度相关的高阶连续理论中，该体积与所研究问题的特征空间尺度相对应，为了方便描述，本文称之为特征体积。原子模拟结果表明[62,67]，晶格失稳首先从涨落最大的晶格原子开始，然后迅速波及周围原子导致初始塑性或相变的出现。因此，解释晶格层次的失稳时，特征体积应该定义在原子尺度。现考虑一个简单的无限晶格，以X为中心的一个小体积（VX）的自由能的二阶展开为

根据式(14)和式(15)，可以得到如下线性近似关系

接下来，考虑该小体积在虚的均匀小应变场扰动下自由能的变化，即式(18)对 δE取一次变分，截断到二阶小量，并注意应变梯度也会随着应变场扰动的出现而发生一个小的变化，可得

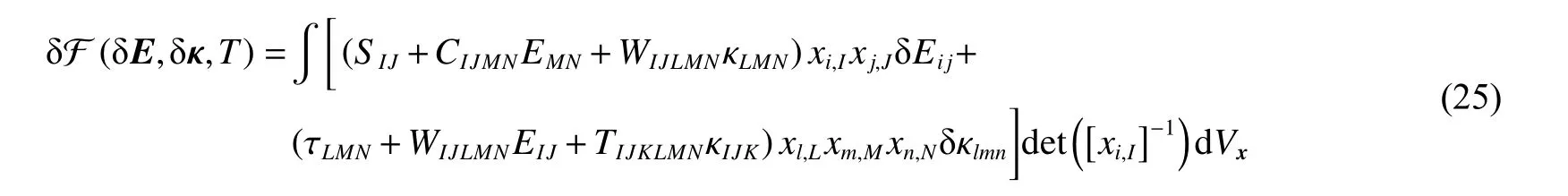
将式(23)和式(24)代入式(25)，并化简保留至应变或应变梯度扰动的二阶小量，得到

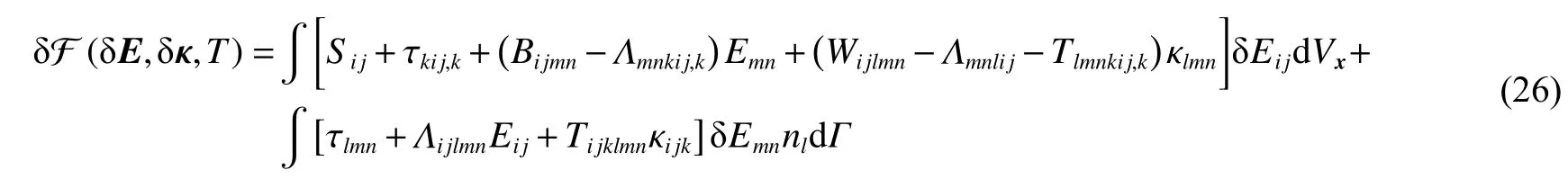
式中： Γ为小体积的外表面，其单位法向量为n，B和 Λ的定义如下

式(26)中等号右边的第2 个积分代表体积外部材料通过表面对该体积内材料的能量贡献，若仅考虑材料内部（远离边界部分）的稳定性，表面的影响可以忽略，因此体自由能密度的变化为

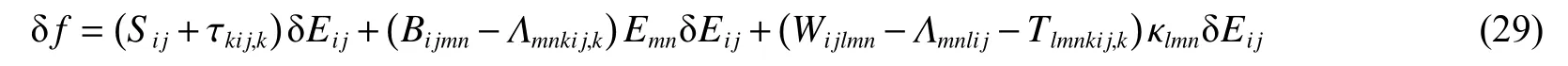
式(29)中等号右边第1 项等于平衡态下单位体积内外力所做的功，即

式(29)中等号右边第2 项和第3 项为晶体中存储的应变能密度。形变的晶体要在小的应变场扰动下保持稳定，其应变能密度在任意位置（对应于任意应变）处必须为正，即

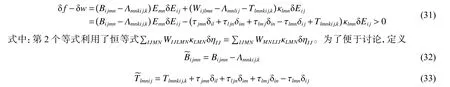
则晶体稳定性条件（式(31)）变为

2.2.3 应变-应变梯度耦合模型的微观基础

要利用2.2.2 节中的应变-应变梯度耦合模型来判断晶体的弹性稳定性，需要知道晶体在当前形变状态下的各阶弹性系数张量。然而，梯度相关的弹性系数在以前的高阶连续理论中仅作为一个调和量，用于拟合一些已知的结果。王昆等[62,66]从原子尺度系统地提出了一种计算各阶弹性系数张量的静力学方法，并指出2.2.2 节所采用的现象性理论模型的微观理解及其适用范围。求解高阶弹性系数的基本思路：将体系受到应变及应变梯度扰动的能量表示成应变和应变梯度的函数，为此首先需要将ΔU用位移及其各阶梯度表示，然后再利用关系式(14)～式(17)。在假设近邻原子数不变的前提下，经过一系列繁杂的代数运算，最终可得

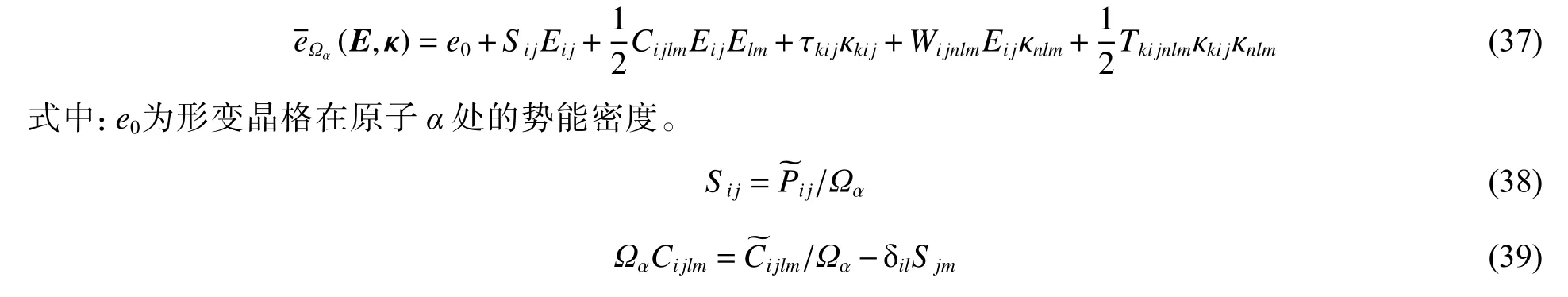
根据2.2.2 节的分析，微观势能密度对应于连续尺度的应变能密度，因此，在等温条件下，式(37)与式(18)中自由能密度的各项相对应，由此可得晶体高阶稳定性条件（式(34)）所需的各阶弹性系数张量。由式(40)、式(51)、式(45)及式(46)可知，对于中心对称类型的晶体， τ和W恒为零。此外，值得注意的是，上述晶体各阶弹性系数仅仅依赖于晶体的当前应变，与应变梯度无关，因为这里选取的特征体积是空间某格点处的单原子体积，由于微观原子排列的离散性，应变梯度的概念仅仅在特征体积包含多个晶胞的情况下才存在，因此，此处提供的弹性系数计算方法仅仅适用于受到小应变梯度扰动的均匀形变晶体，或者用于不均匀形变晶体的局部弹性稳定性分析。前一种情况在进行静态理论模型分析中经常遇到，如2.2.2 节的应变梯度稳定性分析；后一种情况在原子模拟结果分析中会遇到，本节的结果相当于提供了一种局域晶格弹性稳定性的分析方法。结合本节中各阶弹性系数张量的计算方法与2.2.2 节建立的应变-应变梯度耦合模型，预测了斜波压缩单晶铁在极端应变率下的临界失稳应变，如图12 所示。从图12 中可以发现，改进的波恩准则预测的应变失稳点在B处（见图12(b)），基于应变-应变梯度耦合模型的高阶失稳准则预测的失稳点在A处。NEMD 模拟结果（见图12(a)）表明，当应变梯度低于10−3Å−1时，晶体失稳首先发生在A处，与高阶失稳准则的预测结果一致。在更高的应变梯度下，失稳点逐渐偏离模型预测结果，这是由于 ～B和 ～TL是在小应变梯度扰动假设下得到的，用于高应变梯度情况时误差较大。

2.3 初始微结构对相变的影响

晶体缺陷对相变的影响是多方面的。首先，从热力学角度看，晶体缺陷处的原子排列混乱，并且缺陷原子具有更高的迁移率，因此在缺陷处通过原子重排形成低能结构的概率比完整晶体要高。其次，从动力学角度看，缺陷引起的晶格畸变能有助于相变的形核。此外，在冲击压缩下，缺陷处可能优先出现塑性，如发射位错、晶界滑移与迁移等，然后发生相变。为了深入认识晶体缺陷对高压相变的影响规律，需要从原子尺度上系统研究缺陷对相变形核孕育时间、相变机制以及塑性与相变微观耦合机制等的影响，MD 模拟已在相关方面取得了大量进展。

2.3.1 初始孔洞缺陷

邵建立等[68]研究了有纳米孔洞（约2 nm）存在时不同冲击强度对相变形核时间的影响（见图13），发现形核时间与过压程度之间满足指数关系，与冲击波实验研究结果[69]一致。此外，他们还采用均匀压缩技术进一步比较了一维和三维应变下温度对相变形核的影响，发现一维应变条件下的形核压力阈值明显低于三维应变情况，并且两者随温度升高的变化趋势截然不同[70]。崔新林等[71]研究了含有纳米孔洞的单晶铁的冲击相变，观察到了孔洞附近沿[100]压缩与(011)[0 11]剪切的相变机制，导致相变首先在孔洞附近形核并形成蝴蝶状图案（见图14）。这些研究都是基于Voter-Chen 势的结果，缺乏相变前的塑性行为。Wu 等[72]使用MAEAM 势研究了含圆柱形孔洞的单晶铁的冲击取向效应，发现沿[110]与[111]晶向冲击时，孔洞附近首先出现位错环发射现象，然后发生相变，而沿[001]晶向冲击时没有观察到位错。

图13 相变形核时间与过压程度（ Δp）的关系：(a)有纳米孔洞存在时MD 模拟结果[68]，（b）实验结果[69]Fig. 13 Nucleation time of phase transition versus overpressurization observed in(a) MD simulations at presence of a nonvoid[68] and (b) experiments[69]

图14 相变在纳米孔洞附近的形核（红色表示hcp 原子，黄色表示bcc 原子，其他颜色为非晶原子）[71]Fig. 14 Nucleation of phase transition around a nonvoid, where red denotes hcp atoms,yellow denotes bcc atoms and the other color denotes amorphous atoms[71]

2.3.2 晶 界

Gunkelmann 等[73]分别采用Mendelev 势（无相变）和改进的Ackland 势（有相变）模拟了多晶铁的冲击响应行为，观察到随冲击强度的增大冲击波由弹塑性两波结构到弹性-塑性-相变三波结构的转变，其中塑性通过形成位错环-穿过晶界-留下螺位错的机制进行，如图15 所示。王昆等[67]采用MAEAM 势模拟了不同冲击强度下纳米多晶铁的冲击相变行为，发现纳米多晶铁在冲击下具有两种截然不同的相变耦合模式，并依赖于相变-塑性/形变耦合机制。第1 种为应力援助类型的相变耦合模式，该模式在单晶铁中也观察到了；第2 种为应变诱导相变耦合模式。其中，应力援助相变耦合模式分两步进行，首先沿相变不变平面的<001>晶向压缩形成六角密排结构，然后通过密排面间的穿插形成新相，是机械能贡献相变驱动力的过程，在MD 模拟的应变率范围内，这种相变模式通常以晶格过压失稳引起的无势垒形核的形式出现，相变所需的宏观压力阈值较高；而应变诱导相变耦合模式中的两个步骤在时间上是重叠的，相变形核源于晶体的局域变形和能量弛豫，即相变可以在形变过程中产生的局域应力集中处形核，形成低能结构，降低体系的局域应力，以响应外部的施加载荷，这种相变模式所需的宏观压力阈值较低。

图15 在0.7 km/s 的冲击速度下加载15 ps 时多晶铁样品的局部结构（图中仅显示缺陷原子，颜色代表原子离观察者的距离）[73]Fig. 15 Local structure of polycrystalline iron at 15 ps under the shock with a impacting velocity of 0.7 km/s,where only defect atoms are shown (The color represents the distance from the observer.)[73]

王昆等[74]研究了初始孪晶与相变的相互作用，发现孪晶激活的相变比单晶铁更容易发生（见图16），但是两者的相变变体选择规则都满足最大转变功准则，这与共格孪晶界缺乏界面位错使得界面附近的应力较均匀有关。在此基础上，张学阳等[75]进一步研究了 Σ5和两种类型的 Σ3（扭转与倾斜）晶界的冲击响应，发现相变变体选择规则均满足最大应变功准则，然而只有沿两种 Σ3晶界冲击时相变前有明显的位错活动（见图17）。由于 Σ5样品的冲击方向为[001]，而两种 Σ3样品的冲击方向分别为[110] 和[111]，晶界附近出现位错活动的冲击晶向与含孔洞的单晶铁一致[72]，因此推断在冲击下缺陷附近位错的活动主要与单轴应变加载的晶向有关。

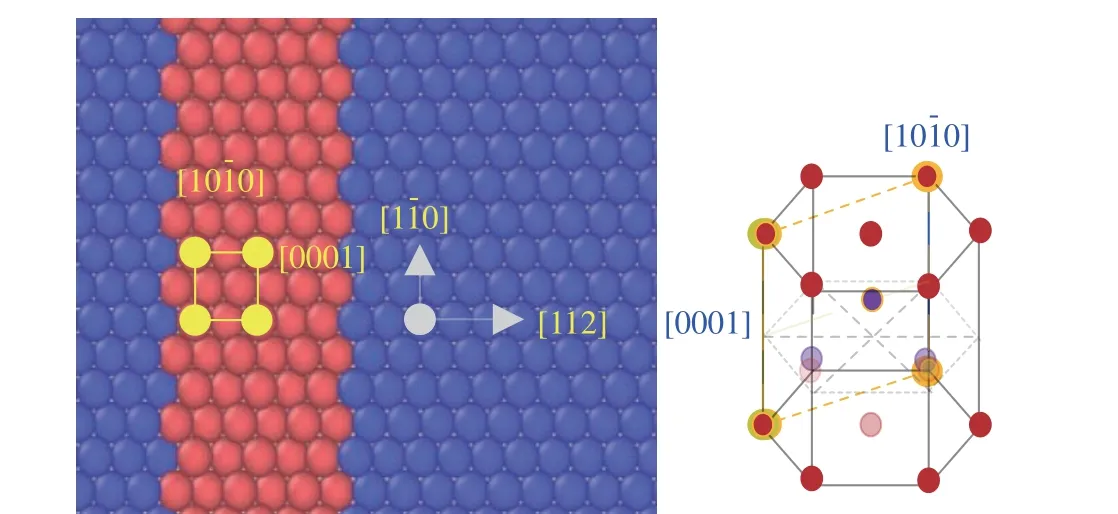
图16 含有孪晶的双晶铁样品在最大粒子速度为0.4 km/s 的斜波压缩下31 ps 时的局部构型（红色表示hcp 原子，蓝色表示bcc 原子，右图hcp 晶胞中黄色的原子面对应于左图中黄色方框标记的原子面）[74]Fig. 16 Local configuration of bicrystal iron sample containing a twin at 31 ps under ramp compressions with a maximum particle velocity of 0.4 km/s (Red denotes hcp atom and blue denotes bcc atom. The right figure shows a unit cell of hcp phase,where the yellow atomic face corresponds to the atomic face marked with yellow square in the left figure.)[74]

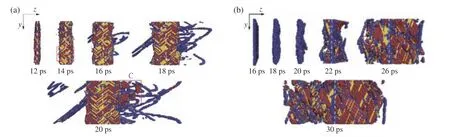
图17 在0.5 km/s 的粒子速度下 Σ3扭转晶界(a)与 Σ 3倾斜晶界(b)的冲击塑性与相变（冲击波沿z 方向传播，在两种样品中分别对应于<110>和<111>晶向）[75]Fig. 17 Shock-induced plasticity and phase transition of Σ3 twist grain boundary (a) and Σ3 tilt grain boundary (b)under the shock with a particle velocity of 0.5 km/s, where shock wave propagates along z direction,corresponding to <110> and <111> crystallographic direction, respectively[75]

2.3.3 位 错

位错是实际晶体中一类非常重要的晶体缺陷。高压相变在预存位错处的形核问题非常值得关注然而相关的原子尺度研究非常少。最近，Huang 等[76]研究了含刃型位错单晶铁的冲击塑性与相变行为，观察到位错的活跃滑移系从{110}<111>到{112}<111>的转变。铁的相变发生在位错滑移系启动之后。图18 显示了受塑性控制的相变机制，其中与单晶铁的相变机制的差别在于沿[001]晶向压缩过程中(110)面绕[111]晶向发生了一定角度的转动，造成最终相变变体的取向与单晶铁的相变变体存在一定差异。事实上，对于一些更高尺度的方法，如多场耦合的相场模型[77–78]，位错与相变相互作用的微观机制，尤其是晶体形变学上的机制，对于发展基于物理的微力学模型至关重要。目前，仍缺乏该方面的相 关基础研究工作。，

2.4 逆相变与层裂

铁的高压相变是可逆的，研究相变-逆相变的规律对于理解冲击后回收样品中的微结构特征具有重要意义[79]，同时对金属材料加工及后处理技术也具有重要的指导意义[10]。层裂发生在冲击波从后表面反射卸载阶段，源于反射卸载波与入射稀疏波相互作用而产生的巨大拉伸应力，当拉伸应力超过材料的抗拉强度时，材料将出现损伤和断裂。显然，铁的逆相变发生在层裂行为之前，因此逆相变留下的微结构将直接影响材料的后续拉伸断裂行为。

形变孪晶是bcc 金属中常见的一种塑性形变机制，动态相变前产生的形变孪晶与相变的相互作用对材料微结构及其形貌有重要影响，关系着材料的宏观动态力学行为，这也是理解含相变材料动力学行为的物理基础。王昆等[74]从原子尺度研究了双晶铁中垂直和平行孪晶与相变的相互作用，发现垂直孪晶在经历一次正相变和逆相变之后可以完全“恢复”，即存在记忆效应，然而恢复孪晶的尺寸被显著细化了，这为加工制造超细纳米孪晶材料提供了一种可能的途径；当加载强度足够高时，相变产物中出现滑移带，导致恢复孪晶中出现一些二次孪晶；这些细化孪晶的尺寸分布取决于孪晶-相变的过渡势垒。对于平行孪晶界，在相变过程中形成大量滑移带，导致逆相变孪晶出现几乎所有可能的变体，从而在恢复样品中留下类似于正六边形的特征孪晶结构。

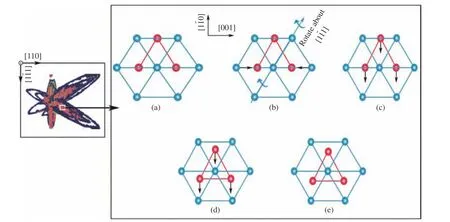
图18 受塑性控制的相变（bcc→hcp）过程示意图（红色与蓝色原子分别位于相邻的两个原子面上）[76]Fig. 18 Schematic diagram showing the plasticity-controlled bcc→hcp phase transition,where the red and yellow atoms locate in two adjacent atom planes[76]

Gunkelmann 等[4]采用准等熵压缩技术研究了多晶铁的压缩与卸载行为，观察到了类似于实验恢复样品中的bcc 孪晶[79]，通过跟踪原子运动轨迹，发现残留孪晶的出现与逆相变过程中的剪切作用有关。在二次压缩下，孪晶会消失，然后再发生相变。铁相变对层裂行为的影响研究也有一些进展。通过对比无相变（Machová势）与有相变（改进的Ackalnd 势）的原子间相互作用势的模拟结果，发现相变降低了多次层裂和裂纹形成的可能性[80]（见图19）。关于铁层裂的原子模拟工作还非常少，实验方面却取得了不少进展，并且非常有必要结合原子模拟方法进行解析。例如，激光冲击实验发现[81]，低温下铁的层裂具有脆性断裂特征，而高温下层裂面上出现了很多小面结构，表明层裂过程中有很多直裂纹的传播，既有晶间断裂，又有穿晶断裂，并且分布范围可达几十微米（见图20）。目前，这种断裂模式发生转变的原子尺度机制还不清楚。此外，冲击波实验还观察到纯铁的反常“二次”层裂，与相变对冲击波传播的影响有关[82]，晶格层次的机理仍需进一步探索。

图19 采用Machová势(a)和改进的Ackland 势(b)得到的多晶铁层裂的MD 模拟结果[4]Fig. 19 Spallation of polycrystalline iron by MD simulations using (a) Machová potential and (b) modified Ackland potential[4]

图20 激光冲击实验回收的铁样品：(a)样品初始温度293 K，层裂面处的最高加载状态处于α→ε相变边界上；(b) 样品初始温度673 K，层裂面处的最高加载状态处于两相共存区[81]Fig. 20 Iron samples recovered after laser shocks (a) at 293 K, where the maximum loading state of the spall plane is on the α→ε phase transition boundary, and (b) at 673 K, where the maximum loading state of the spall plane locates at the two-phase-coexistence region[81]

3 非平面冲击载荷下的结构相变

在冲击波加载技术中，除了易于实现、应用最广泛的平面冲击外，还有柱面冲击、球面或准球面冲击等非平面动态加载[83]。例如：武器中的弹体结构多采用圆柱壳结构，弹体爆炸过程中外壳受到的就是典型的柱面动态载荷；柱面内爆磁通量压缩实验装置中的金属套筒在工作过程中受到的柱面会聚冲击载荷[84]；在惯性约束聚变中，球形燃料靶丸受到严格控制的球面会聚冲击[85–86]。与平面冲击相比，非平面冲击载荷（柱面冲击、球面冲击或准球面冲击）的应变条件更复杂，材料的微观响应也明显不同。例如：在球面和准球面会聚冲击波下，纯铁的塑性变形主要以滑移形式发生，而球面冲击条件下试样内部形成的局部变形带和微孔结构明显多于准球面冲击[87]。再如，多晶铜在球面会聚冲击波作用下，在高强度冲击中出现空位位错环，而在低强度冲击[88]中却未见空位位错环[89]。单晶铜在柱面会聚冲击波作用下，位错形核位点与冲击波速度有关[90]。此外，对304 不锈钢应变诱导马氏体相变的研究发现，马氏体变形体的形成强烈依赖于应力条件[91]。在相同的应变下，多轴（双轴或三轴）加载比单轴加载产生更多的马氏体变体。受实验加载和检测手段的限制，到目前为止，有关非平面冲击载荷下材料结构、塑性和相变等响应行为的研究还比较少，Asay 等[92]在2017 年出版的专著《Impactful Times: Memories of 60 Years of Shock Wave Research at Sandia National Laboratories》的展望部分，明确提出要发展研究复杂冲击条件下材料响应规律的实验技术和理论方法。

对于非平面的柱面和球面冲击来说，由于冲击面的大小随着时间的延长而变化，因此适用于平面冲击的活塞加载、对称撞击等方法均难以直接应用于柱、球面加载中。类比平面冲击加载模拟中采用刚性活塞以一定速度撞击靶材产生冲击波的基本思想，胡望宇课题组通过引入钝化势能面与原子间的相互作用来实现加载。在柱面冲击模拟中，柱状势能面的半径以一定速率收缩（或膨胀），实现柱面内爆（或外爆）冲击加载（见图21）。柱状势能面与原子之间的相互作用描述为[90]

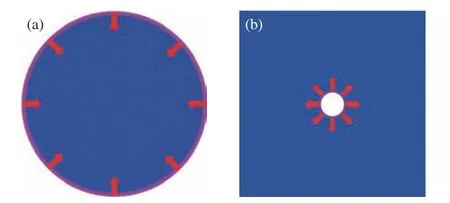
图21 柱面内爆(a)和外爆(b)冲击加载示意图（蓝色表示试样，紫色圆环表示柱形势能面，红色箭头表示加载方向）Fig. 21 Schematic diagram of the shock loading by cylindrical(a) implosion and (b) explosion (The blue part represents the sample, the purple ring represents the energy surface of the column, and the red arrow represents the loading direction.)

式中：K为力常数，K= 1 nN/Å2；θ(r−R)为标准阶跃函数；R为圆柱形势能面的半径（内爆加载时R随时间线性减小，外爆加载时R随时间线性增加）；r为原子到柱状势能面中心轴的垂直距离。冲击模拟采用微正则系综（NVE）。

单晶Fe 的柱面内爆冲击（柱面轴沿[001]晶向）模拟研究发现，在低冲击强度下，由于晶体的各向异性特征，尽管施加的是圆柱面形会聚冲击，冲击波前的形状由开始的圆柱面逐渐转变为方柱面（见图22）。同平面冲击相比，材料在柱面冲击下受到的应变约束完全不同，材料内部单元之间存在相对运动，冲击压缩区的应力和温度分布要复杂得多。在沿<110>方向的塑性变形区域出现了典型的1/2<111>位错环，相变在位错环区域形核。冲击相变过程中形成了大量的相变孪晶（见图23）。

图22 （a）柱面轴沿单晶Fe [001]晶向在内爆冲击下垂直于柱面轴的横截面内的原子速率分布，（b）10 ps 时垂直柱面轴横截面内的局域温度分布Fig. 22 (a) Atom velocity distribution in the cross section perpendicular to the cylindrical axis under implosion impact along [001] direction of Fe single crystal, and (b) the local temperature distribution in the cross section perpendicular to the cylindrical axis at 10 ps

图23 柱面轴沿单晶Fe [001]晶向在内爆冲击下（vp = 0.6 km/s）局域微结构随时间的演变（红色表示hcp 结构原子，绿色表示以层错形式出现的fcc 结构原子，灰色表示位错线周围的其他结构类型的原子，为清晰起见，未相变的bcc 结构原子已被删除）Fig. 23 Evolutions of local microstructures with time under the implosive impacting with the cylindrical axis along [001] direction of Fe single crystal (vp = 0.6 km/s) (Red indicates hcp atoms,green indicates fcc atoms in the forms of stacking faults, and gray indicates other atoms distributed around dislocation lines. For clarity, bcc atoms without phase transition have been removed.)

对比柱面内爆形成的会聚冲击，外爆冲击过程中冲击波前随时间的演化而增大（见图24），波前的冲击强度明显降低。在<110>的4 个等价方向上，没有观察到位错环的出现，但在相变波前有类似于沿[110]晶向平面冲击时的位错运动。柱面外爆时，在持续的冲击载荷下，可以观察到bcc-hcp-bcc-hcp 循环相变，hcp-bcc 的逆相变导致bcc 相相对于初始时出现了45°的重定向。在铁的bcc-hcp 相变中，剪切应力驱动原子在{110}滑移面中移动。在平面冲击载荷下，当{110}滑移面平行于冲击方向时，在单轴应变形成的强侧向约束作用下，会产生垂直于冲击载荷的剪应力。相反，柱面发散冲击载荷下，应变是多轴的，导致产生多个垂直于应变主轴的剪应力，使hcp 变体c轴取向多样化，不再局限于典型的<110>方向（见图25）。

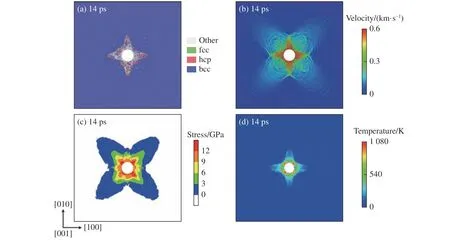
图24 柱面外爆冲击后试样内局域微结构、速度波剖面、应力波剖面和温度分布Fig. 24 Local microstructure, velocity profile, stress profile and temperature distribution in the sample after cylindrical explosions

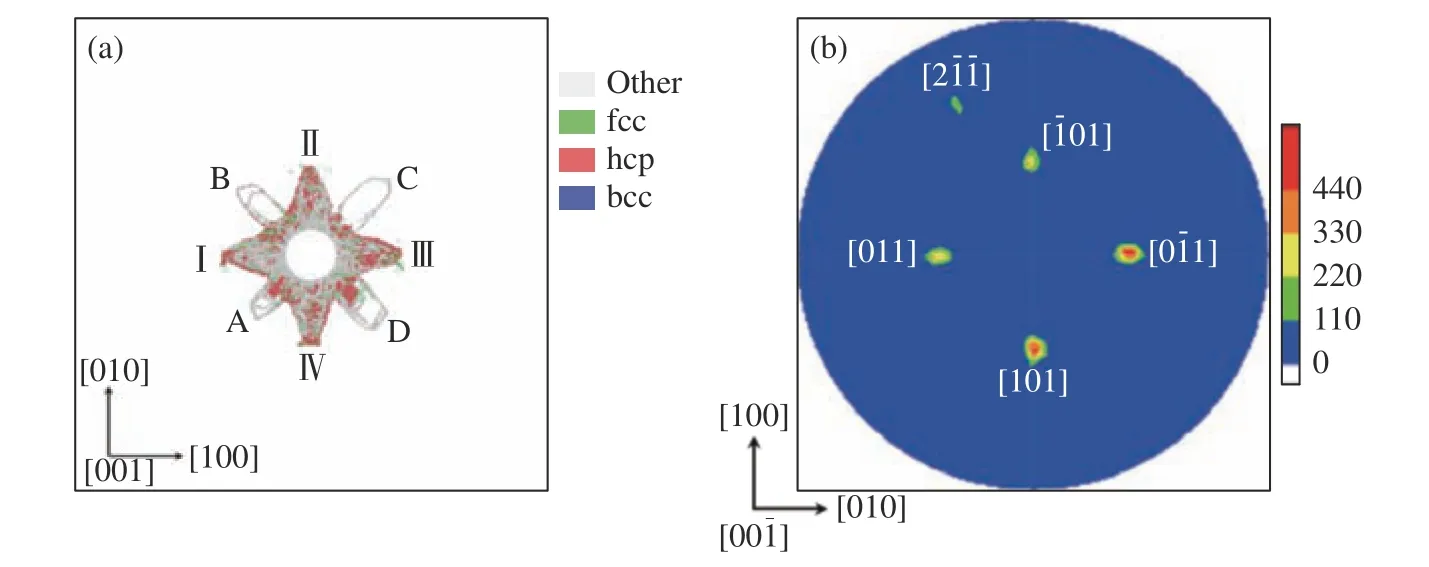
图25 柱面外爆冲击后试样内部的局域微结构(a)以及hcp 相变变体c 轴取向极图(b)Fig. 25 Local microstructure inside the sample (a) and polar figure of the c-axis showing different hcp variants (b)

4 结论与展望

本文综述了动态加载下铁相变的原子模拟研究现状，尤其是近年来随着新的原子间相互作用势被广泛应用于铁高压相变的原子模拟研究，铁在各种不同加载条件（包括冲击晶向、冲击强度、应变率等）与初始微结构（如初始位错、孪晶界及一般晶界等）下的相变机理不断被发现，已初步形成加载条件-相变晶体学机制-变体类型选择-产物织构间的定性认识。得益于铁的势函数的改进，高压相变与塑性微观耦合机制研究已成为该领域中新的研究方向，对于一些基于物理的微力学建模具有重要的指导意义，同时也是理解含相变金属材料动态力学性能不可或缺的一部分。已有的研究表明，相变前的塑性与加载晶向及缺陷类型密切相关，对后续相变机制与形核有重要影响。然而，目前还未形成完整的认识，仍需针对不同类型的晶体缺陷进行系统的模拟研究。介观尺度的方法在描述晶体的高压相变与塑性方面取得了长足的进展，如基于反应路径的相场模型[93–95]已具备较强的动态力学响应行为预测能力，基于经典密度泛函理论的晶体相场模型[96–97]可以直接获取介观时间尺度的相变与塑性的原子机制，这些模型与MD 模拟方法一起，能够完全覆盖材料在微介观时空尺度上从原子分辨到连续尺度的动态力学响应。此外，相变与层裂也是材料动力学行为研究的一个重要方向。原子模拟在这方面的研究非常少，其中一种可能的原因是缺乏相关晶格尺度原位诊断实验的支撑。

尽管原子模拟在铁动态相变研究中已经取得了丰硕的成果，但是还存在至少如下几方面的不足，甚至矛盾。其一，现有的两种可以正确描述铁 α↔ε相变的势函数在描述冲击塑性方面存在一些明显的差异。改进的Ackland 势可以预测出单晶和多晶铁的变形孪晶，但只在多晶铁中观察到位错，而MAEAM势可以预测单晶铁的冲击塑性，但没有出现相变前的形变孪晶，澄清这些问题需要更多晶格层次的原位实验观测。其二，目前的原子模拟研究主要以基于晶体学的机理认识为主，对相变动力学的理解仍然以经典的各向同性的形核理论为依据，在理论上几乎没有实质性的发展。此外，需要系统地研究材料的动态力学行为与原子间相互作用势的关系，从势函数出发理解材料动态力学行为机制发生的原因无疑极其重要：一方面，有助于进一步改进原子间相互势函数，指导开发其他材料的高压原子势函数，助力材料基因工程的发展；另一方面，有助于从热力学上整体把握材料力学行为与体系基本物理性质之间的关系，这对于发展其他基于能量泛函的更高尺度模型（如相场模型等）具有直接的理论指导价值。