绝热剪切变形中温升现象的研究进展

胡 博，郭亚洲,2，魏秋明，索 涛,2，李玉龙,2,4

（1. 西北工业大学航空学院，陕西 西安 710072；2. 陕西省冲击动力学及其工程应用重点实验室，陕西 西安 710072；3. 北卡罗莱纳大学（夏洛特）机械工程系，美国 北卡罗莱纳 夏洛特 28223-0001；4. 西北工业大学民航学院，陕西 西安 710072）

绝热剪切是材料在受到冲击载荷作用时出现的剪切变形高度局部化现象，常见于高速切削[1–2]、金属成型[3]和弹体侵彻[4–5]中。其中，“绝热”指该过程的时间尺度非常短（通常为几十微秒），绝大部分塑性功转化为热量且来不及散失，可近似看作未与外界发生热量交换，因此认为该过程是绝热的。部分材料在发生绝热剪切局部化后会产生一条明显区别于其他区域的窄带，称为绝热剪切带（Adiabatic shear band，ASB）。由于绝热剪切局部化的产生被认为是材料失效的前兆，因此研究绝热剪切具有重要的科学意义和工程应用价值。

1878 年，Tresca 进行了绝热剪切现象的最早相关研究，在经锤打锻造的铁棒表面发现了“X”形迹线，称之为热线（Heat lines）[6]。直到1944 年，随着Zener 等[7]相关工作的发表，人们才对绝热剪切现象有了较清晰的认识。当材料在绝热（高应变率）条件下产生一段应变增量时，应变硬化会导致应力升高，而温度升高软化会引起应力降低，当前者的升高不足以补偿后者的降低时，应力-应变曲线的斜率为负值，此时会产生绝热剪切带。此后，大量学者对相关问题进行了深入的研究和报道。

1992 年，Bai 等[8]系统介绍了绝热剪切局部化的形成以及相关理论和应用。该著作于2012 年再版，补充了此间20 年关于绝热剪切局部化的最新进展和前沿，内容包括绝热剪切局部化现象的实验方法、微观表征以及ASB 相关的数值模拟和理论研究，同时还详细介绍了剪切局部化理论在侵彻、颗粒材料、大块金属玻璃、聚合物和地质等相关方面的应用[9]。Wright[10]于2002 年出版的专著则侧重采用数学方法和特殊解方法阐述绝热剪切行为，讨论了数值模拟和解析方法的相互关系，并对这一复杂的非线性问题进行了简化描述。Meyers[11]在其著作《材料的动态行为》中重点介绍了热塑性剪切失稳的本构模型。Antolovich 等[12]基于大量的实验和模型研究介绍了应变局部化产生的原因及其引发的疲劳和失效。国内外还有ASB 的微观结构[13–15]、实验技术[16]、失效破坏[17]、红外温度测量[18]及研究进展[19–22]等方面的相关报道。

材料温度升高是绝热剪切变形过程最重要的特点[23]。ASB 产生前、后以及产生过程中都会出现温升现象，而绝热剪切带往往是变形和产热最集中的区域，也是出现破坏的前兆区域[9]，因此，研究绝热剪切失效过程中的温升对深入了解材料在高应变率下的塑性变形行为、预测和预防绝热剪切失效具有重要价值。然而，绝热剪切变形的瞬时性特点给温升研究带来了很大困难，导致该方面的研究进展缓慢，直到近年来高速测温技术、高速摄像技术以及数值模拟方法的快速发展，才产生了一系列新的研究成果。然而，目前仍缺乏对绝热剪切变形过程中温升研究的针对性归纳和整理以及系统讨论温升对剪切带及其周围区域影响的综述性论文。鉴于此，本文将重点总结并讨论绝热剪切变形过程中的温升效应。我们将温升分为均匀变形阶段温升、剪切局部化引起的温升和剪切带形成后热传导引起的附近区域的温升3 个不同阶段，从理论计算、数值模拟、实验测量和微观形貌4 个方面对绝热剪切现象中的温升研究进行系统性整理和讨论，以期对现有研究进行较全面的总结，并为后续研究提供参考。

1 理论计算

绝热剪切变形过程中温升计算的本质是求解热-力耦合问题。根据能量守恒定律，温度升高所需的热量来源于材料变形时外力所做的塑性功。现有关于绝热剪切温升的理论计算方法主要分为两类：基于功热转化的温升估算法和基于热传导的温度场估算法。前者主要用于计算剪切带出现之前均匀变形过程的温升，后者则关注剪切带形成后热传导引起的绝热剪切带附近区域的温升。

1.1 基于功热转化的温升估算

温升的功热转化估算方法源自被研究系统的导热方程。材料在冲击载荷的作用下产生变形，根据能量守恒，这一过程中涉及的能量包括材料不可逆的塑性变形功、可逆的弹性变形功，还包括系统与外界的热交换，最终导致材料温度升高。据此，热-力耦合条件下的瞬时热方程[24–25]为

式中：功热转化系数下标“diff”表示微分（Differential）。该表达式体现了温度变化率和塑性功率的比例关系，是与时间相关的率形式，得到了广泛应用[26–28]。将式（2）中的分子和分母同时对时间积分，转化为能量形式，功热转化系数的积分（Integral）表达式 βint可表示为

式中： ΔT为温升； βint为塑性功转化为热的比例，即Taylor-Quinney 系数[29]。功热转化系数的积分和微分形式不同，例如 βint的取值范围为0～1，而βdiff则可能大于1[25,30]。下文中只涉及Taylor-Quinney 系数的积分形式（ βint），将其简写为 β。

由式（3）可以看出， β的大小由材料的塑性变形功、温升以及物性参数（密度、比热容）决定，整理式（3）可得

通过设定式（4）中的 β，可估算材料绝热变形过程的温升。例如，当金属材料受到高应变率加载时，通常β取0.9[1]，这意味着金属材料的大部分塑性变形能都转化为热的形式，又因为该过程历时很短，产生的热量来不及散失而不断积累使材料出现热软化进而失效。式（4）中单位体积的塑性功一般通过对材料应力-应变曲线的积分获得，利用上述关系可计算4340 钢[31]、Ti-6Al-4V[32–34]、铝合金[35]、镁合金[32,36]、钨[37]、超细晶材料[38–40]等金属材料在动态加载条件下的绝热温升。除此之外，还可以通过确定材料的本构关系，得到应力-应变关系的表达式，再将应力转化为应变的函数进行积分求出塑性功。例如，利用实验数据拟合的Johnson-Cook（J-C）本构关系， β取0.9 时，可计算材料在动态加载过程中的绝热温升[41–45]。与之类似，通过Zerilli-Armstrong（Z-A）本构关系，可计算钢和铜的绝热温升，其 β值亦取0.9[46–48]。Pérez-Prado 等[49]对比了上述两种本构模型对钽和钽-钨合金的拟合结果，发现由于J-C 本构对较高应变下材料应力水平的过高估计导致据此计算的温升高于Z-A 本构计算的结果。绝热温升理论计算的相关结果见表1。

表1 基于功热转化理论的绝热温升计算结果Table 1 Calculation results of adiabatic temperature rise based on thermomechanical conversion

从温升表达式可以看出，功热转化系数的选取直接决定了温升的计算结果。因此，许多学者对不同材料 β的取值进行了研究和讨论，总结于表2 中。值得注意的是，由于材料的非均匀变形会使不同位置的温升也存在差异，导致 β值的计算更加复杂，因此表2 中列出的温升和计算得到的功热转化系数均对应材料均匀变形阶段，并不涉及变形局部化以及绝热剪切带的形成。

由式（3）可知，确定功热转化系数 β的关键在于求解或测量外力塑性功以及试样的温度升高值。外力塑性功一般可通过真实应力-应变曲线下的面积积分获得，而试样温度升高值的获取方法则较困难。Kapoor 等[50]测定了钽钨合金（Ta-2.5%W）在3000 s−1应变率下的应力-应变曲线，并采用红外测温装置测得了试样表面的温度变化曲线，同时也计算了该应变率水平下 β为1 时的理论温升，发现理论温升高于红外测温实验结果。为了校验实验测温结果的准确性，采取冻结实验（限制应变加载）的方法，将加载到同一应变（0.32）的试样冷却至室温后，分别加热到图1 中的红外测量温度（85 ℃对应曲线）和理论计算温度（115 ℃对应曲线）进行二次加载，并与直接加载到两次应变之和的对照实验所得的应力-应变曲线进行比较。结果显示，理论计算温度下的二次加载曲线与对照实验的重合度较高，说明实验测得的试样表面温升低于实际情况，并推测该材料的功热转化系数近似为1。他们还参考Mason 等[24]的研究发现，在纯钛、OFHC 铜、6061铝（T6）、1018 钢等其他材料中，在假设塑性功全部转化为热时的温度下，材料的二次加载流动应力与一次加载至较大应变下的流动应力的重合性较好，进一步证实了 β近似为1 的结论。此外，Rittel等[51]在纯钽的高应变率实验中记录了试样表面的温度变化历程，通过计算发现，其功热转化系数在变形过程中近似为1，从而用更准确、更全面的实验设计对Kapoor 等[50]的结果进行验证。他们还提出，这一结论对有明显动态应变硬化的材料不适用，因为不能忽略应变硬化对材料微观结构的改变。

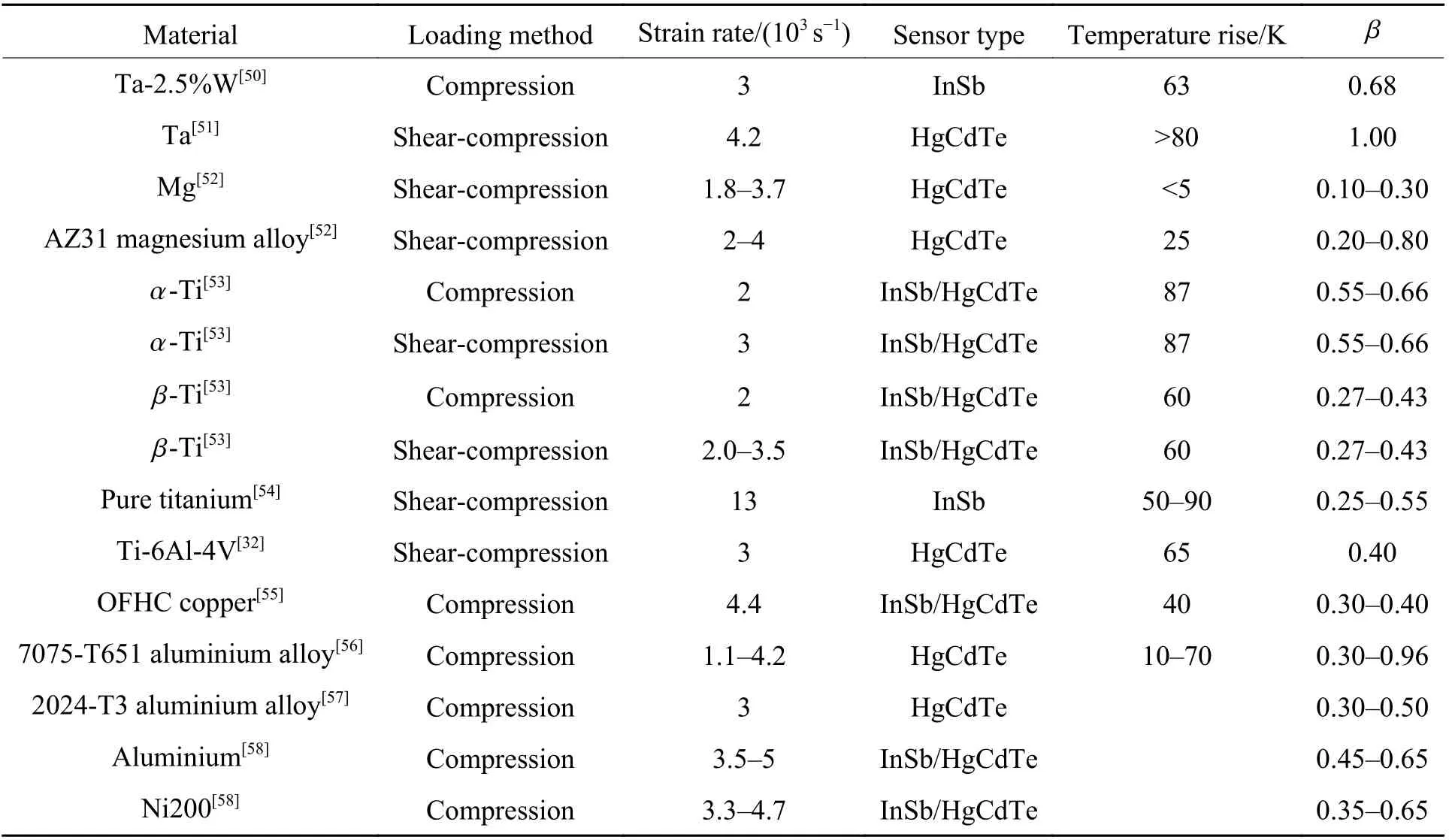
表2 功热转化系数研究总结Table 2 Research summary on Taylor-Quinney coefficient

然而，有些实验发现， β的取值不总接近于1。Ghosh 等[52]通过实验和计算发现，动态加载条件下，AZ31 镁合金功热转化系数的变化范围为0.20～0.80，而纯镁则为0.10～0.30，远远小于1。如图2(a)所示（其中ED、TD、LD 分别表示加载时沿着材料的挤出向、横向和纵向），合金化、晶粒尺寸以及加载方式对镁基金属的功热转化系数有明显的影响。Rittel 等[30]系统测定了不同加载模式（动态拉伸、压缩、剪切）下7 种金属材料的表面温升变化历程，并求得了材料均匀变形过程中Taylor-Quinney 系数的变化情况，如图2(b)所示。可以看出，不同材料的Taylor-Quinney 系数值在0～1 区间内离散分布，没有呈现出集中于某个数值附近的规律。并且对于CP Ti 等材料， β值的大小与加载方式密切相关，这种差异可能与孪晶调节的塑性变形机制有关。

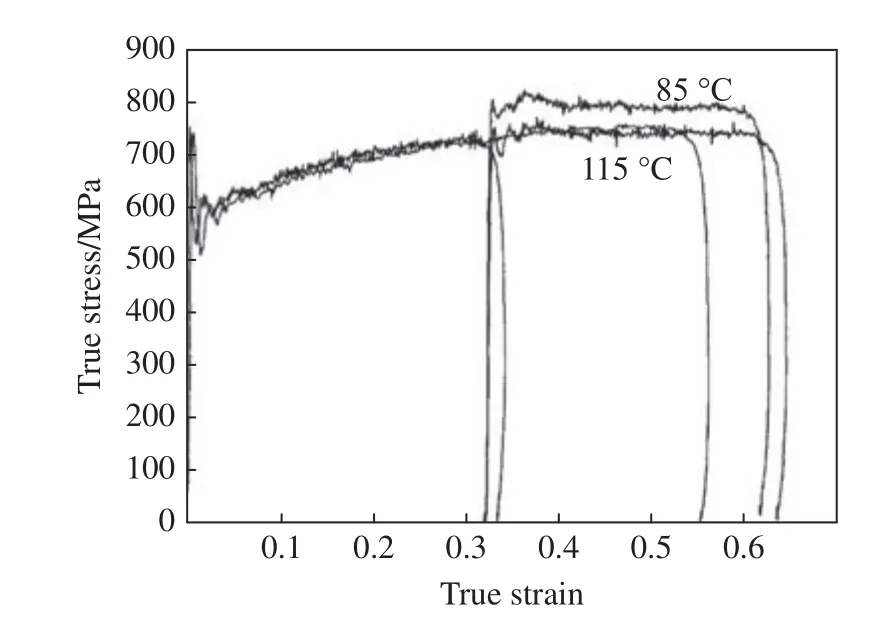
图1 Ta-2.5%W 合金限制应变（0.32）后不同温度下二次加载曲线与单次加载应力-应变曲线比较[50]Fig. 1 Comparison of secondary loading curve and single loading ture stress-ture strain curve at different temperatures while Ta-2.5%W alloy was limited strain (0.32)[50]

图2 （a）不同应变率、加载方式下镁基金属的功热转化系数[52]，（b）不同材料在不同加载方式下的Taylor-Quinney 系数范围（C、T 和S 分别代表压缩、拉伸和剪切3 种加载模式）[30]Fig. 2 (a) Work heat conversion coefficients of magnesium based metals under different strain rates and loading modes[52],(b) Taylor-Quinney coefficient range of different materials under different loading methods(C is compression mode, T is tension mode, S is shear mode.)[30]

一般认为，金属材料在冷加工作用下产生塑性变形时：一部分塑性变形功转化成热并以温升的形式体现，根据前文功热转化系数的定义，该部分能量为总塑性功的 β倍[59]；另一部分能量则储存在材料内部，导致材料内部微观结构发生变化，称作冷加工储存能（Stored energy of cold work），占总塑性功的1– β倍，冷加工储存能可以通过试样受载后的微观组织特征计算。最近，Nieto-Fuentes 等[58]对纯镍和纯铝两种面心立方结构金属的动态力学行为、表面温度演化以及加载后的微观形貌进行了实验测量，同时建立了基于位错理论的本构关系，研究发现两种材料的动态力学行为特点以及加载后的微观形貌类似，模型计算也拟合较好，但是不同应变率（3 000～5 000 s−1）下表面温升的实验结果和计算结果却有较大差别，且两种材料的 β值体现出明显的应变率效应。基于此，他们提出，决定材料功热转化系数的关键因素为微观结构的演化过程，而非变形后微观结构演化的结果，即冷加工储存能。不同于Nieto-Fuentes 等提出的基于位错的本构模型，Lieou等[60]借鉴Langer 等[61]提出的统计热力学位错理论来描述金属剪切局部化过程中的动态重结晶行为，并通过仿真得到了加载后AISI 316L 不锈钢帽型试样截面的Taylor-Quinney 系数分布，如图3 所示。可以直观看出，试样截面的功热转化系数取值范围为0.64～1.00，且越靠近剪切区， β值越大。该结果说明，Taylor-Quinney 系数不仅随加载时间变化，而且在试样上的不同区域也有差别，这种空间分布差异是试样处于非均匀变形阶段决定的。

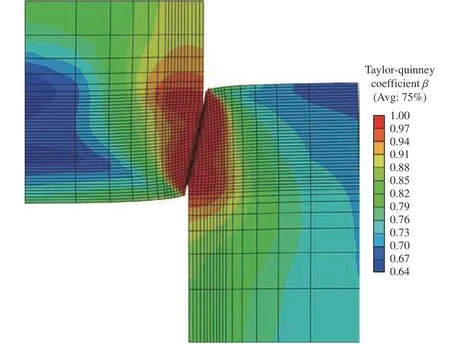
图3 动态加载后功热转化系数在帽型试样截面的分布[55]Fig. 3 Distribution of work heat conversion coefficient in the cap specimen cross section after dynamic loading[55]

从上述分析可以看出，Nemat-Nasser 用间接比较的方式发现，在假设塑性功全部转化为热时的温度下，几种材料的二次加载应力-应变曲线更接近材料的真实情况，据此得出这几种材料的 β值近似为1。而Ghosh 等[52]和Rittel 等[30]用直接测量的方式测定了不同材料在不同加载方式下的表面温度变化，由此计算出的 β值可能远小于1，且没有明显规律，其大小与加载历程、应变率、加载方式等因素相关。采用间接法（冻结应变法）测定 β值的优点在于可以与宏观实验曲线做比较，因而具有较高可信度；不足之处是仅能获得某一个应变点处的功热转化系数，且不能考虑每段加载时的绝热效应，另外对于应变硬化显著的材料也不适用。采用直接法（直接测温法）则可以获得整个加载历程中 β值的变化历史，从而对功热转化过程有更全面的描述。然而，其最难让人信服的问题在于，红外测温法仅能测量试样的表面温度，这与试样内部温升是否一致以及能否代表整个试样的平均温升，这些问题还没有很好地解决。另一个需要深入研究的问题是，除了转化成热之外，外力功的其他部分“去哪了”，以及能否通过实验对其进行观测。近年来，随着研究方法和相关理论的发展，人们对功热转化系数的理解越来越深刻，这对绝热剪切温升的理论计算提供了很大帮助，但是关于功热转化系数的计算和测量方法仍存在争议，相关领域的研究仍有待进一步发展和完善。

1.2 剪切带及附近温度场计算

准静态加载条件下，试样的变形速率很低，材料塑性变形产生的热有充足的时间通过热传导而扩散，使得试样的温度近似恒定，因此准静态加载常常被称作等温加载。与准静态相比，动态加载提高了试样的变形速率，缩短了热传导时间，因而将其近似为绝热过程。但事实上，“绝热”只是一种理想简化，热传导现象贯穿于材料动态加载的整个塑性变形和失效过程，评估绝热剪切过程中的热传导效应对分析并理解测温结果、微观组织演化以及材料的塑性流动和失效具有重要的作用。

利用设定的数学模型进行分析是计算绝热剪切温升的另一种理论方法，通常用来讨论绝热剪切带形成后对其周围区域的热影响。在进行模型计算前，需要把问题根据需求作相应的简化。按照剪切带几何模型的特点，分为热量池模型和面热源模型进行介绍，两种模型均属于一维热传导模型。

1.2.1 热量池模型

将绝热剪切带视为半带宽为δ、无内热源的热量池，热量池内的温度与带外的温差为T0，求与时间和空间相关的温度场。

为了便于建模和计算，假设材料的导热系数、比热容和密度均不随温度变化，并且只考虑热量沿垂直于剪切带方向的传播。该问题可简化为常物性、无内热源的一维非稳态热传导问题，导热微分方程为

式中： δ为剪切带半宽度。将初始条件式（7）代入式（6），该温升场的表达式为

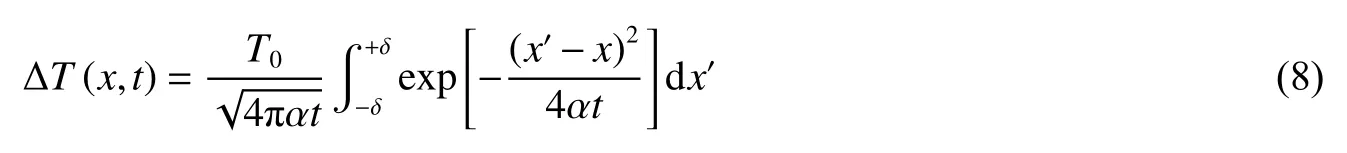
Nemat-Nasser 等[63]参考上述模型，推导出适用于帽型试样、柱形坐标系下的温度场表达式，而且由于剪切带宽度比传热区宽度窄，式（8）可进一步简化为

式中：Ri为帽型试样轴线到剪切带轴线的距离。根据上述表达式估算多晶钽剪切带形成后带内温度的冷却速率（Cooling rate），计算发现在剪切带形成后不到0.1 s 内，带内温度由1 930 K 下降至1 000 K，推测这与剪切区域宽度窄以及金属钽的导热性好有关。Li 等[64]也用相同的公式计算了剪切带中心（x=Ri）的温度变化，绘制了不同晶粒尺寸和初始温度下钛剪切带内的降温曲线，如图4(a)所示。可以看出，尽管晶粒尺寸和初始温度不同，但是剪切带中心的温度在20 µs 内都降至了环境温度，并推测这可能是带内晶粒来不及长大的原因之一。

将温升场的表达式式（8）进行变量代换，得到[65]

Me-bar 等[4]根据量纲关系将式（11）简化，得到了剪切带内温度随时间的变化关系

将式（12）对时间项微分，可以求得剪切带内温度的冷却速率，发现Ti-6Al-4V 弹道冲击后剪切带内的冷却速率达到了107℃/s，并据此解释了特定微观组织的形成原因。可以看出，随着时间延长，剪切带内的温度会降低。以上模型描述的是剪切带温度向带外的扩散过程，没有涉及剪切带形成过程中温度的持续升高，因此只能用来描述剪切带形成后对周围区域的热影响。

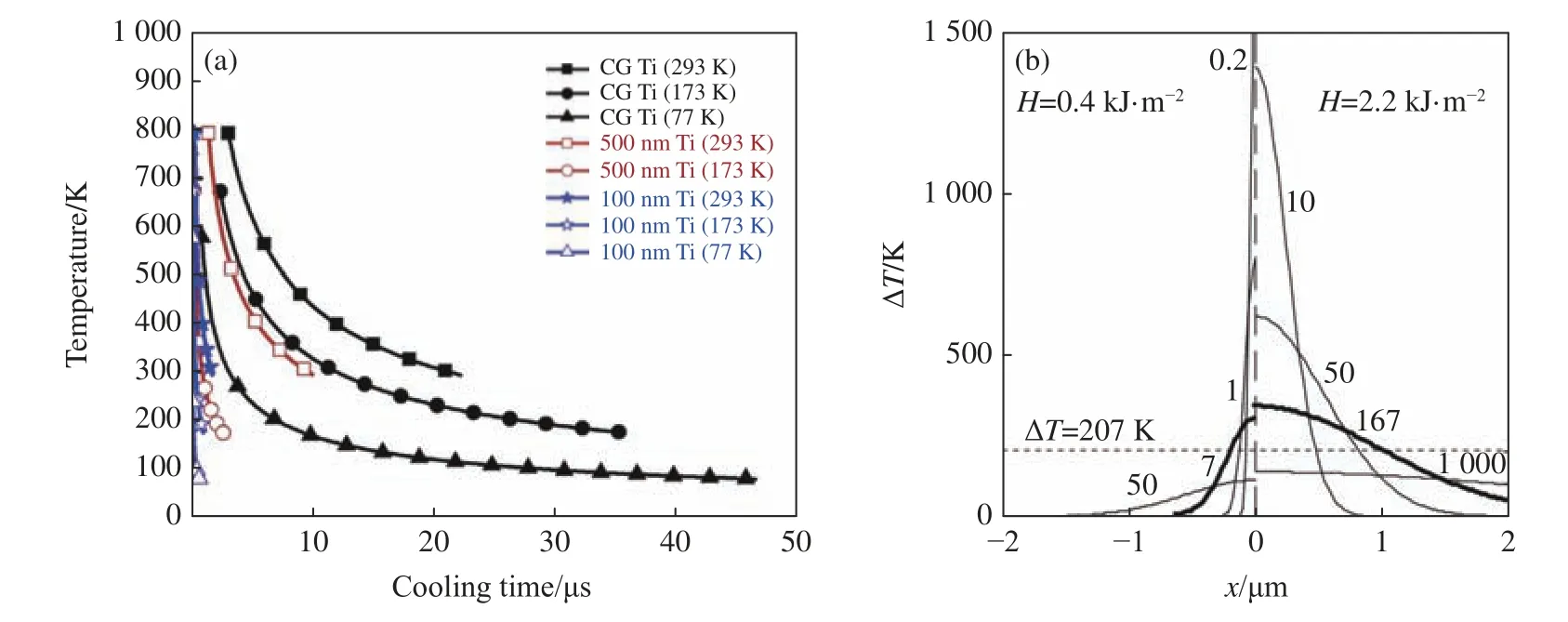
图4 （a）钛在不同晶粒尺寸和初始温度下剪切带内的降温曲线[64]， （b）金属玻璃剪切带附近不同时刻的温升分布[66]（时间单位为ns）Fig. 4 (a) Ti cooling curves in shear band with different grain size and initial temperature[64], (b) temperature rise distribution at different times near the shear band of metallic glass[66] (t is in nanoseconds)

1.2.2 无厚度面热源模型

根据持续作用时间不同，将面热源问题分为瞬时面热源和持续面热源两类讨论。瞬时面热源问题可描述为：将剪切带视为无厚度的瞬时面热源，已知该热源产热的强度，计算热源处（剪切带内）和热源以外区域的温度分布。

Lewandowski 等[66]对金属玻璃中剪切带的温升进行了测试和模型计算。在试样表面涂抹一层易熔的金属锡，根据实验后金属锡的熔化情况反推出剪切带的热影响范围，得出金属玻璃中剪切带热影响区域的半宽度为0.2～1.0 µm。在模型计算中，将剪切带近似为厚度为零并向无限大介质传热的瞬时面热源。这样，只需给出该面热源的热含量和其他物性参数就可以得到温升 ΔT关于距热源距离x和时间t的关系式

式中：H为热源面密度，单位J/m2，对于不同的剪切带宽度，热源面密度的取值不同； α为热扩散系数，单位m2/s。将不同的热源密度数值代入式（13）中，得到两种面热源密度下剪切带附近不同时刻的温升分布，如图4(b)所示。令式（13）中x=0，得到剪切带内部的温度变化函数

值得注意的是，由于上述模型中热源为瞬时面热源，并不在时间上持续作用，所以剪切带内温度的表达式关于时间是递减的，因此该模型描述的是剪切带形成后带内温度的降低和周围区域的温度变化。该方法不仅可用于求解热传导，还可以处理与物质扩散相关的问题。例如土壤中放置一块污染源，污染物质向土壤的扩散过程也可以参考这一问题的解答过程[67–68]。

持续面热源问题可描述为，在一个半无限大的固体上，将剪切带视为无厚度、热流密度为常数的持续面热源，计算带内温度的变化。该问题的传热学解析解[69–70]为

式中：F0为热源的热流密度，单位W/m2。热流密度是传热学概念，根据能量守恒，Wright 等[71]将式（15）转化为

式中： τ为切应力，u˙p为剪切带平面的塑性位移速率。由于实验中切应力和塑性位移速率都随时间在变化，因此只适用于很小的时间间隔，并认为在该时间段内其值恒定，否则将不满足能量守恒。可以看到，尽管式（15）和式（16）的形式不同，但都描述了剪切带内的能量转化。Wright 等[71]利用式（16）计算出金属玻璃在最终破坏时的温升为280 ℃。

本节介绍了剪切带及其附近温度场的模型计算方法。其中，热量池模型具有相对成熟的热传导求解方法，可描述剪切带形成后的全区域温度变化。无厚度面热源模型中，瞬时面热源模型可以研究剪切带形成后自身温度的降低及其对周围区域的影响，而持续面热源模型多用于描述剪切带内的温升过程。通过热量池模型和无厚度面热源模型的对比，可以发现后者多用在脆性材料的剪切带温升研究中，原因可能是脆性材料中剪切带宽度较窄，有的甚至在纳米尺度，此时忽略其宽度更贴近实际情况。

数学解析法对绝热剪切温升以及剪切带对周围区域热影响的计算等方面都起到了一定作用。该方法的优势在于其结果可以用函数形式表达，形式简练、直接。另外，微分等连续函数形式还方便对表达式进行进一步处理以获得更多信息。但是模型计算的精度受到模型选取的影响，例如，在实际情况下，剪切带的宽度往往是随加载历程变化的，而模型中一般设置为常数。另外，初始条件和参数的选取也会影响计算结果，如带内外温度的设定，各物性参数的取值等，这些条件或参数的取值也难以准确确定。因此该方法一般用于对绝热剪切温升的粗略估计，并不能提供精确的结果。

2 数值方法

第1 节的理论计算部分介绍了绝热剪切温升计算的功热转化法和数学解析法，可以对绝热剪切变形过程中的温升进行粗略估计。但是有些实际问题的模型较复杂，此时理论计算已无法满足精确计算的要求，需要借助数值模拟方法求解。

本节将介绍绝热剪切中温升研究的3 种数值方法：一维瞬态热传导问题的基本解法，用于处理绝热剪切带产生后周围区域温度的演化；热力耦合计算方法，主要是摄动分析法，用于计算绝热剪切温升；有限元计算方法，用于绝热剪切温升计算，并给出了计算的基本步骤和简单例子。

2.1 一维热传导

这里提出一种在绝热剪切带形成之后评估绝热温升影响的思路，结合功热转化计算或实验测温的结果，仅用数值方法模拟绝热剪切带产生后的热传导过程。该思路的优势在于可以评估绝热剪切带内温升带来的影响，作为对前文中剪切带理论最大温升后续热影响的补充和完善。

忽略固体表面与空气间的换热，只发生固体热传导过程，并且认为试样同一截面表面的温度与内部一致。为了方便计算，可将剪切带视为温度均匀的热量池，只考虑绝热剪切带形成后带内温度沿垂直于带边缘方向的扩散，即处理一维热传导问题。按照数值模拟方法的基本步骤，先将前文中传热微分方程式（5）的两端离散化，对等号左侧时间项（非稳态项）向前差分，对等号右侧扩散项取中心差分，得到导热方程的数值求解形式[62,72]

以上差分格式的收敛性条件为温度项的系数值恒正，即对时间步长和空间步长的选取提出了一定的要求。这样，在时间和空间（一维）组成的空间坐标系中，只要设定好初始条件和边界条件（包括剪切带内、外的初始温度和剪切带内温度的变化），就可以通过迭代算出不同时刻、不同位置处离散点的温度值。将这些离散点连起来就构成了T(x,t)的空间曲面，也就完成了该热传导问题的求解。

值得注意的是，热传导方法描述的是剪切带温度向带外扩散的过程。该方法用较简单的方式解答了前面提到的剪切带温升影响范围的问题，且过程易于用编程的方法实现，可以达到较高的时间和空间精度。为了进一步追求结果的准确性，还可以在迭代过程中考虑比热容、导热系数等物性参数随温度的变化，先得到这些物性参数和温度的关系，再更新每步计算出温度值所对应的物性参数值，作为下一步时间间隔内的值代入计算即可。

2.2 热力耦合计算

此处的热力耦合计算方法主要指摄动分析法（Perturbation method）。该方法最早用于流体动力学中的失稳分析。诸多学者将该方法用于绝热剪切失稳分析中，用来回答失稳在何时何地发生的问题。摄动分析法的一般步骤：首先，简化目标问题的计算模型，列出所研究问题的控制方程组（一般包括动量守恒、能量守恒、本构关系等），给出原方程组的解；其次，在该解的基础上添加扰动项（单一添加或同时添加），扰动项一般是位置与时间的函数；最后，将新解代回原控制方程组，经过适当的简化得到扰动方程组，给出受扰动影响的各变量的解。

Bai[73]采用摄动分析法对纯剪切条件下的热塑性失稳进行了数值求解，重点讨论了热软化主导下的失稳模式，并据此提出了由材料常数组合的反映其抵抗剪切失稳的临界应变判据。Clifton 等[74]也采用相同方法对绝热剪切带的产生进行了摄动分析，并给出了不同塑性剪切应变下温度的空间分布，如图5(a)所示，可以看到明显的温升局部化历程。Walter[75]采用摄动分析法对绝热剪切带的产生进行了一维数值模拟，采用4 种不同的塑性流动本构模型描述热软化因素的影响。图5(b)是4 种模型剪切带的中心温度随名义应变的变化关系，温度的急剧升高表明发生了剪切局部化，通过对比可以看出不同热软化模型控制下局部化发生的名义应变不同，且局部化前和局部化后的带内温度变化也有明显差异。Wright 等[76]通过在均匀场中施加温度扰动模拟了剪切带的产生，图6(a)是其模型中心位置处应力、温度和塑性应变率随时间的变化关系，纵坐标归一化应力指当前应力与粗晶铁准静态流动应力的比值，归一化温度指当前温度与初始温度的比值。可以看出，几乎在同一时间应变率和温度发生了陡升，而应力则骤降，标志着剪切带的产生。Wright[77]改进了传统摄动分析法中扰动方程组的解法，并首次提出了局部化产生的临界温度准则。

除了以温度扰动作为摄动分析的初始条件外，其他扰动也可以用来触发绝热剪切带，并导致温度升高。Guo 等[78]在Joshi 等[79]工作的基础上，提出了纳米晶和超细晶金属动态加载条件下绝热剪切带形成的几何软化机制，图6(b)为其数值模拟得到的纳米铁剪切带内应力和温度的演化，可以看出，在名义塑性应变接近6% 时出现了明显的应力突降，并伴随温度的陡升，这标志着剪切局部化的发生。Zhou 等[80–81]采用特征线法求解高阶控制方程组，在提高计算精度的同时保证了计算效率，在模拟剪切带产生的同时研究了多条剪切带的相互作用，并且得到了剪切带产生时应力、温度和应变率的演化。

图5 （a）CRS-1018 钢在不同塑性应变下温度的空间分布[74]，（b）4 种热软化模型描述的剪切带中心温度随名义应变的变化（ θ表示带内温度与环境温度的差，图例表示不同热软化模型函数）[75]Fig. 5 (a) Temperature profiles of CRS-1018 steel at different plastic strain[74], (b) relationship between the shear band center temperature and nominal strain described by four thermal softening models （ θ is the difference between the temperature in the band and the ambient temperature. The legend shows the different heat softening model functions.）[75]

图6 （a）模型中心处应力、温度以及应变率随时间的变化[76]，（b）纳米铁剪切带内应力和温度的演化[78]Fig. 6 (a) Time dependence of stress, temperature and strain rate at the center of the model[76],(b) evolution diagram of internal stress and temperature in shear band of nano-iron[78]

2.3 有限元方法

有限元方法的本质是解偏微分方程，对于初始条件边界条件复杂的实际问题，有限元方法可以通过时间和空间离散化将问题转化到单元节点上，结合初边界条件使这些局部问题可解，再经过有限次迭代和循环得到整个问题的近似解。有限元方法处理复杂问题的优势在于可以根据需要对变量进行精确的场输出。

杨扬等[82]描述了有限元方法研究绝热剪切温升的一般步骤：首先，根据实验结果拟合材料的本构关系；其次，建立有限元模型，输入初边界条件、材料各物性参数以及功热转化系数，进行有限元热力耦合分析；最后，根据需要输出仿真结果并进行分析讨论。基于类似思路，诸多学者对各种复杂工况下不同材料的绝热剪切温升进行了有限元计算。

Zhou 等[83]用有限元仿真的方法研究了非对称冲击载荷下预置缺口平板绝热剪切带的萌生和传播，他们对剪切韧性失效采用率相关的临界应变准则，并设置了临界拉伸应力控制失效。图7为仿真得到的一定冲击速度（v）下不同时刻沿剪切带方向的温度分布曲线，可以看出，在距缺口9 mm范围内为温升显著区域，且该区域内的最大温升达500 K。此外，还发现垂直于剪切带上下各1 mm内的区域内温度升高明显，该结果与红外测温结果一致。

Chichili 等[84]对带有缺口的圆筒试样在动态压-扭载荷下的绝热剪切行为进行了数值仿真。采用率相关的幂指数本构关系，功热转化系数值设置为0.9，物性常数参考手册值随温度变化，并且忽略整个过程发生的热传导。图8(a)为试样中面的温度分布云图，可以看到明显的温升局部化，并且最大温升出现在靠近入射杆端的缺口拐角处，与实验所得结果一致。Bronkhorst 等[85]对钽和不锈钢帽型试样在动态载荷下的剪切局部化进行了实验研究和有限元仿真，得到了两种材料在变形过程中的温升分布及其变化历程，图8(b)为其仿真得到的不锈钢在不同时刻剪切区域的温度分布云图，可以明显看出温升局部化，且最高温度达1670 K，达到了该材料的熔点。而另一种材料钽中则未形成明显的剪切带，其剪切区的温度只有该金属熔点的23%～28%。

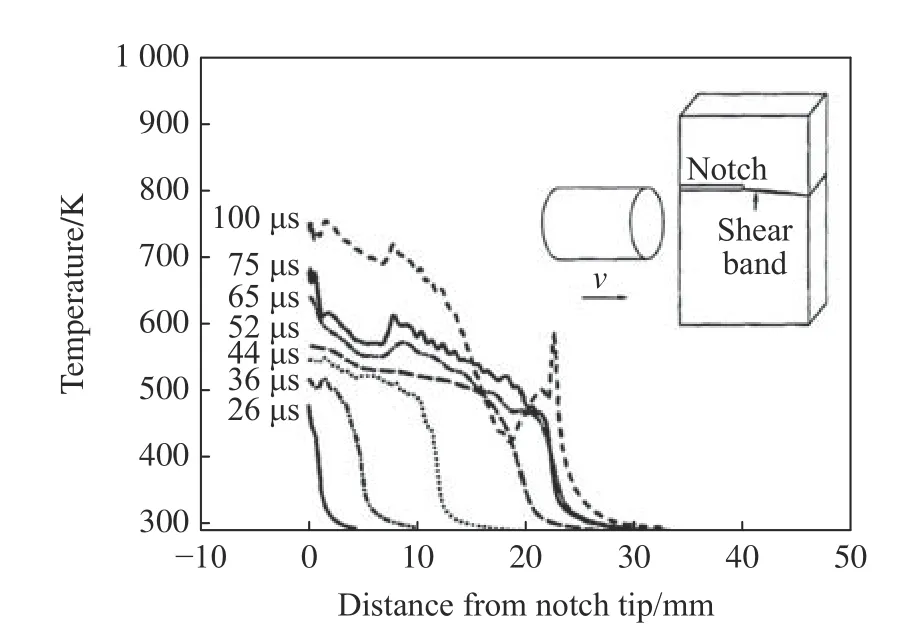
图7 25 m/s 下不同时刻沿剪切带方向的温度分布曲线[83]Fig. 7 Temperature profiles along shear band line at different times after 25 m/s impact[83]

图8 （a）动态扭转有限元计算试样中面的温度分布（图例中由蓝色到红色温度逐渐升高）[84]，（b）不同模拟时刻（25、30、35、40、45 µs）不锈钢剪切区域的温度分布[85]Fig. 8 (a) Computed contour plot of the temperature distributions within the specimen near the notch tip at the end of the simulation[84], (b) profile of temperature at 316L stainless steel at different simulation times (25、30、35、40、45 µs)[85]

Xu 等采用新型双剪切试样测试了603 钢[41,86–87]、紫铜[88]和Ti-6Al-4V[89]在高应变率（103～105s−1）下的力学性能，并结合高速摄影、有限元仿真以及加载后的微观表征等方法对这几种材料绝热剪切区的应力、应变状态和失效形式进行了分析。虽然并未给出试样剪切区的温升分布图，但其有限元计算体现了在场输出上的优势，弥补了高速摄影和测温只能获取试样表面信息的不足。Zhu 等[90]也用类似方法对Ti-6Al-4V 试样在动态压剪、拉剪和纯扭转等加载条件下绝热剪切带的萌生进行了分析，讨论了应力状态对绝热剪切临界应变的影响。

从上述研究中可以看出，有限元方法可以帮助我们分析绝热剪切中包括温升分布在内的应变局部化现象和材料内部应力状态等，有助于对绝热剪切现象进行全面、深入地分析。同时，我们也要看到，以上方法都是直接模拟包括剪切带产生过程在内的热-力耦合过程，其模型较复杂，而且受限于材料本构关系和失效模型的精度，这种方法一般只能模拟绝热剪切带形成及之前的过程，之后的仿真结果（如应力-应变关系）往往与实验结果有较大差距[85]，因此无法准确评估局部温升带来的热影响。

3 温升的原位测量

评估绝热剪切过程中温升的最直接方法是实验测量。但是，由于绝热剪切过程对测温设备在微秒级时间尺度、微米级空间尺度下的高精度测量要求，因此相比于理论和数值方法，原位测温技术起步较晚。

目前，温升的测量方法主要分为两类，接触式热电偶测量法和非接触式红外测量法。其中，使用热电偶测量时，将工作端（热端）与被测物体接触，通过与自由端（冷端）形成温度差从而在由两种不同材料组成的闭合回路中形成电动势，根据电动势与温度的函数关系制成的分度表实现温度测量。非接触式红外测量方法的基本原理：一方面，根据Stefan-Bolzmann 定律，任何温度大于绝对零度的物体都会向外发出热辐射，且辐射力的大小与温度的四次方成正比[18]；另一方面，根据光电效应，光敏元（一般为半导体材料）可将接收到的入射光信号转化为电信号，只要找出二者的对应关系即可得到被测物体的温度[91]。两种测试方法相比，热电偶测量方法的操作相对简单，温度测试范围更大且不局限于表面温度测量；红外测量法的优势在于响应时间更短且为非接触式测量，不会改变被测物体的测试状态[92]。

3.1 热电偶测量法

热电偶测量法主要用于测定材料（包括聚合物、复合材料和部分金属等）动态塑性变形初期产生的绝热温升。由于温升的接触式测量法依赖于被测物体和热电偶之间的热传导过程，因此其测试的响应时间受热传导速率的影响。Rabin 等[93]通过理论模型计算得出：要得到被测物体瞬时温度响应的有效数据，热电偶的热扩散率至少要比被测物体的热扩散率大一个数量级。鉴于热电偶电极一般采用金属材料，因此该方法在测量热扩散率更小的聚合物和复合材料温度时更为有效。

Chou 等[94]将直径小于1 mm 的珠形热电偶工作端嵌入聚合物柱形试样的中心，对其在低、中、高应变率范围（10−4～103s−1）变形过程中的温度变化进行测量，获得了试样内部的温升演化。图9(a)为其中一种测试材料聚甲基丙烯酸甲酯（PMMA）在不同应变率下的应力和温升随应变变化曲线。其中，最高应变率的温升曲线通过理论计算得到，用虚线表示。可以看出，该材料的温升和应力均体现出明显的正应变率相关性，并且温升在应力的流动段开始近似线性显著增加，在应变率为760 s−1时估算的最大温升约为16.7 ℃。此外，他们通过实验测试了该热电偶的时间响应，证实了其测试结果的可靠性。Rittel[95]将工作端直径为127 µm 的T 型热电偶嵌入聚合物盘形试样内部，使用分离式霍普金森压杆（SHPB）装置进行动态加载，并结合理论模型对热电偶的测温效果进行了评价。测温结果显示该热电偶工作的响应时间约为10 µs，为热电偶测量法在其他材料中的高速原位测温应用奠定了基础。Rittel[25]采用相同的测试方法对聚碳酸酯（PC）盘形试样进行了动态原位测温实验，其中一种工况下应力和温度随应变的变化关系如图9(b)所示。可以看出，在应力近似线性升高的过程中没有观察到明显的温升，而当应变达到0.2 时，试样内部的温度陡升，并产生了应变软化现象，其加载过程中的最大温升为29 ℃。Sassi 等[96]研究了胶接复合材料连接件的动态压缩力学性能及动态加载过程中其表面和内部的温度演化。他们将直径为120 µm 的热电偶工作端分别粘贴在试样表面和内嵌于试样中心，通过加载和测试首先得出这种测温方法的响应时间约为10 µs，可以满足瞬态温度的实时观测要求；其次，他们发现试样表面的测温结果与应力的演化基本同步，而试样内部的测温结果则滞后，并且在低应变率下不会出现温升信号；最后，通过对比试样表面和内部的温度变化，得出这种复合材料在动态压缩加载条件下内部和表面的损伤演化是不均匀的，其内部出现温升的条件是某种损伤模式的产生和积累。

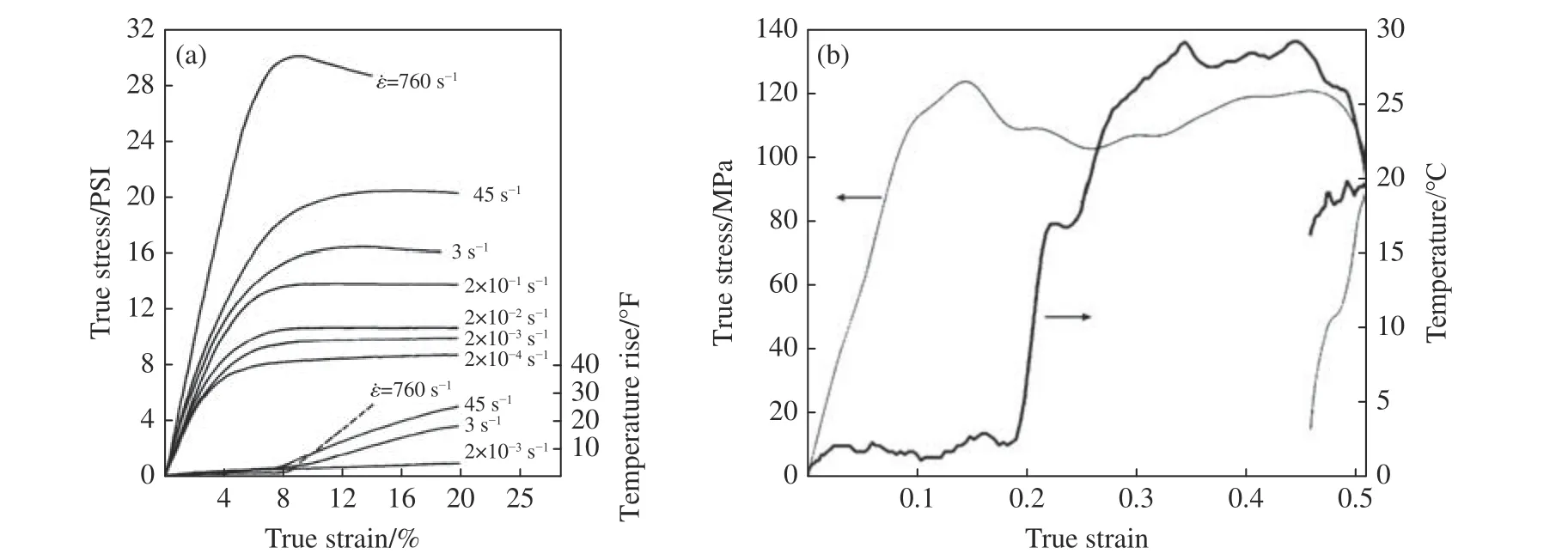
图9 （a）PMMA 在不同应变率加载条件下的应力-应变关系以及温升-应变关系[94]，（b）PC 盘形试样动态加载（平均名义应变率为6 500 s−1）条件下应力和温升随应变的变化关系[95]Fig. 9 (a) Stress-strain and strain-temperature-rise curves for PMMA at various strain rates in compression[94], (b) true stress-true strain and temperature rises for PC disk 41 (Nominal average strain rate is 6 500 s−1)[95]

Cao 等[97–98]记录了铁基形状记忆合金在准静态和动态加载条件下的表面温度演化。为了获得更短的响应时间，采用尖端厚度仅为80 µm 的T 型热电偶，并进行了温度补偿。图10(a)显示了非弹性应变和热电偶温度信号随时间的变化关系，可以看出当非弹性变形停止增加时测温信号也随之下降，表明该热电偶的响应速率较快，可以满足同步测试的要求。图10(b)则给出了不同加载速率和加载方式（压缩和拉伸）下试样表面的温升-应变关系，通过对比分析，形状记忆合金在压缩和拉伸加载下的温升均表现出正应变率相关性。

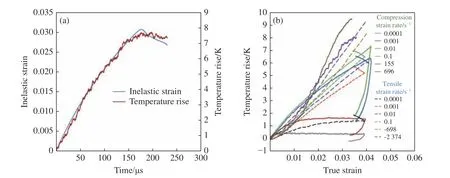
图10 （a）铁基形状记忆合金非弹性应变和热电偶温度信号随时间的变化[97]，（b）铁基形状记忆合金在压缩[97]和拉伸[98]加载时，不同应变率下试样表面的温升-应变关系Fig. 10 (a) Time history of inelastic strain and change in temperature under compression[97], (b) temperature rise-true strain curves of shape memory alloy under compression[97] and tension[98]

除了测量规则试样动态加载过程中的绝热温升，利用热电偶测温方法还能够研究材料动态断裂过程中的热影响。Shockey 等[99]在预置缺口钢板的预测动态裂纹扩展路线上排布了热电偶测温阵列，采集了不同位置的温度历史，并计算了该材料的动态断裂韧性。其中一个热电偶测得的裂纹扩展路径附近的温升信号如图11(a)所示，可以看到热电偶测得的温升信号在1～2 s 内迅速升至最高值，约0.8 ℃，之后缓慢下降。Rittel[100]研究了预置疲劳裂纹PMMA 的动态断裂行为，采用K 型热电偶，将半径为130 µm的珠形工作端嵌入试样中心，测得裂纹扩展过程中试样内部的温度变化。图11(b)是热电偶测得的裂纹尖端附近温度随时间的变化曲线，可以发现在PMMA 试样发生破坏之前，其内部温度呈先下降后上升的变化过程，而且试样在急速温升过程中发生破坏。Rittel 推测产生这种现象的主导因素是动态起裂过程中的热弹性效应（Thermoelastic effects）。此外，热电偶测温法也可用于金属高速切屑等加工过程中产热的实验测量[101–102]。

综上所述，通过热电偶测试法可测量材料动态加载过程中的绝热温升，但是受限于热电偶接触式的测试方法和导热速率，该方法并没有广泛应用于金属材料动态变形过程中的绝热温升测量。

图11 （a）预置裂纹钢板动态加载过程中裂纹扩展路径附近某处的温度演化[99]，（b）预置疲劳裂纹PMMA 试样动态加载过程中试样内部的温度演化[100]Fig. 11 (a) Measured temperature history of steel data experienced by material near the path of a rapidly propagating crack[99],(b) temperature of PMMA recorded in the vicinity of fracture time[100]

3.2 红外测量法

非接触式红外测温方法可用于金属材料在整个绝热剪切变形过程中的温度测量，包括塑性变形初始阶段的均匀温升、变形局部化阶段的非均匀温升以及绝热剪切带产生后的温度分布等。红外测温方法的关键在于传感器，不同材料的传感器具有不同的敏感性和工作波长范围，对应于不同的响应时间和测温范围。常用的传感器材料包括锑化铟（InSb）、碲镉汞（HgCdTe）、砷化镓（GaAs）等，其中InSb 较适用于测量较高温度，HgCdTe 和GaAs 适用于测量较低温度。

20 世纪80 年代，Marchand 等[103]和Hartley 等[104]开创性地采用阵列式探元测定红外辐射的方法获得了钢在动态扭转加载条件下表面的温度演化。这套温度测量设备由光学系统、红外探测器和数据采集器组成，如图12(a)所示。其中，光学系统不仅可以将试样表面发出的红外辐射汇聚到探测器上，还可以通过适当的光路设计将被测区域放大，使测量结果更加精确；红外探测器使用InSb 传感器，采用了8 个探元组成探测器阵列，工作环境温度为−196 ℃，工作波长范围为0.5～5.5 µm，包含了实验测试的温度范围；探测器采集电压信号，实验前还需用热电偶标定探测器电压值和试样表面温度值。通过测量得到了结构钢动态扭转条件下剪切带附近的温度变化历程，测得结构钢第一次加载后最大探元电压信号对应的温升为595 ℃。但是，由于实验中单个探测器的尺寸为0.53 mm × 1.80 mm，超过了绝热剪切带的宽度，所以探元的输出电压不能直接对应于绝热剪切带内的温升。鉴于此，根据辐射力和温度的关系，换算得出剪切带内的最高温度达到1140 ℃。此外，他们还通过高速摄影技术得到了剪切带形成过程中局部应变的演化，将剪切局部化过程中的塑性变形分为均匀小变形、非均匀大变形和变形局部化3 个阶段，对后续相关领域的研究产生了深远的影响。

图12 （a）绝热剪切温度测量系统[103]，（b）探元阵列测得剪切带附近的温度变化历程[105]Fig. 12 (a) Adiabatic shear temperature measurement system[103], (b) temperature change near the shear zone measured by probe array[105]

Duffy 等[105]以相似的设备为基础，通过改进实现了单个探元尺寸为17 µm 的探测区域宽度，并采用16 个探元组成了测温区域总长度为292 µm 的测温阵列。图12(b)为HY-100 钢在动态扭转载荷作用下试样表面的温度演化。测温结果显示：最大温升点在探元阵列当中，对应的温度接近600 ℃，剪切带周围的温度分布及变化历程也可以从图12(b)中直观获得。除了精确的温度测量，他们还结合试样设计和高速相机得到了试样表面剪切带宽度和对应的局部应变演化。Liao 等[26]采用相同设备对Ti-6Al-4V动态扭转下的表面温升进行了测量，测得其表面最大温升为440～550 ℃。他们还特别提出了对于易氧化材料的温度标定方法，提高了测试结果的可靠性。

Duffy 之后，许多学者在其研究的基础上，通过实验得到了不同加载条件下不同材料表面的温度演化。Zhou 等[106]测量了圆柱形子弹冲击下Ti-6Al-4V 和C-300 钢板中预置缺口前端的温升，图13(a)为冲击实验示意图。采用16 个边长80 µm 的探元组成总跨度为1.5 mm 的单列探元阵列，分别测量了平板缺口前端横纵两个方向的温度，得到了不同冲击速度下缺口尖端的温度场。测温结果显示，Ti-6Al-4V在64.5 m/s 冲击速度下的最高温度为450 ℃，而C-300 钢在42.8 m/s 的冲击速度下，最高温度达1 400 ℃。Gurudu 等[107]建立了由64 个边长100 µm 的温度传感器以8 × 8 形式组成的高速红外测温系统，利用这套系统测量了带有缺口钢板在弹体冲击下预制裂纹尖端的温度场，其实验加载方式与图13(a)相似。他们获得了不同时刻被测区域的温度分布，从中可以直观看到绝热剪切带的二维萌生和扩展过程。图13(b)为冲击加载某时刻试样表面的温度分布，加载端和预制裂纹尖端在左侧，剪切带向右扩展，从中可以看到明显的温升局部化，且最大温升达630 ℃，并表现出漩涡状分布规律。

图13 （a）圆柱子弹冲击带缺口平板加载方式示意图[106]，（b）动态加载裂纹尖端温度场分布[107]Fig. 13 (a) Asymmetric impact configuration and failure mode[106], (b) a high-speed thermal image of a developed shear band[107]

Ranc 等[108]考虑到不同传感器对不同波长范围红外辐射的敏感度不同，为了兼顾高低温测量的准确性，采用了传统InSb 阵列传感器和带有GaAs 光电阴极的数字增强CCD 相机两套测温技术，分别用于Ti-6Al-4V 动态扭转试样不同变形阶段，表面温度在低温（50～300 ℃）和高温（800～1 700 ℃）范围内的测温实验部分结果如图14 所示。从图14(a)中可以明显看出温升局部化的演变过程，对应单条剪切带的萌生，值得注意的是，绝热剪切带产生前附近区域的均匀温升也超过了120 ℃。从图14(b)中可以看出，试样表面温度较高的区域并不连续，与Gurudu 等观察到的温升漩涡分布类似。此外，他们在实验中还发现了多条剪切带同时萌生的现象，但当剪切带开始传播时，由于产生的应力不均，使得其中一条得以进一步扩展。

Macdougall 等[28]采用HgCdTe 红外阵列传感器测量了Ti-6Al-4V 动态扭转和拉伸条件下的温升，测得动态拉伸条件下试样颈缩后和破坏时的最高温升约为200 ℃。Seidt 等[109]采用高速红外相机检测不锈钢在准静态和动态拉伸加载条件下的表面温升，在加载应变率为3000 s−1时，拉伸试样颈缩区的温度在30 µs 内上升了约250 ℃，最高温度达375 ℃。刘永贵等[110]采用单探元HgCdTe 测温传感器对铝合金和形状记忆合金在动态压缩载荷下的表面温度进行了测量，结果显示两种材料的升温和降温曲线有明显差别，同时还分析了塑性功和相变在各自材料温度变化中的作用。

还有研究将测温结果与应力-应变曲线相结合，探讨温升与绝热剪切带形成的因果关系。Rittel 等[32]将测温结果和剪切失效前的各个变形阶段对应，图15(a)为Ti-6Al-4V 压剪试样在动态加载条件下的应力和温度随应变的变化曲线，可以看出在剪切变形第2 阶段开始前温升不明显，之后温度便迅速升高直至破坏失效。在Rittel 工作的基础上，付应乾等[111]采用高速红外测温装置对钛合金帽型试样动态剪切变形过程中剪切区的温度变化进行了同步测量，发现绝热剪切的起始温度低于160 ℃，由此推断绝热温升不是绝热剪切带起始的最主要控制条件。Guo 等[112]对纯钛压剪试样进行了动态同步测温拍照，进一步明确了试样塑性变形和温升的关系，如图15(b)所示，可以看出剪切带形成时探元测试到的温升很微弱，由此推断剧烈温升可能是绝热剪切产生的结果，而非原因。

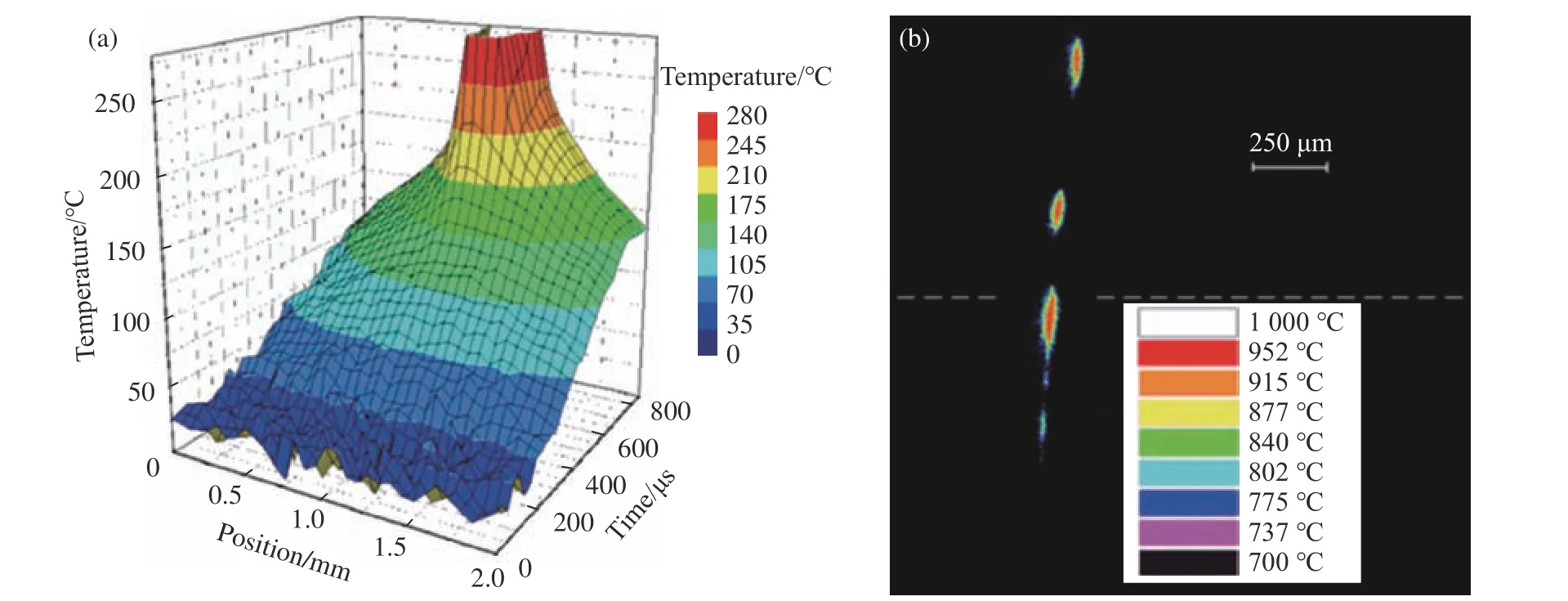
图14 低温传感器测温实验结果（a）和高温传感器测温实验结果（b）[108]Fig. 14 3D temperature visualization at ‘‘low temperatures’’ range (a) and radiance temperature field at ‘‘high temperatures’’ range (b)[108]

图15 （a）Ti-6Al-4V 合金的力学-测温实验结果[32]，（b）纯钛的力学-测温实验结果[112]Fig. 15 (a) Typical stress and temperature vs. strain for Ti-6Al-4V alloys[32],(b) typical stress and temperature vs. strain for pure titanium[112]

综上所述，采用红外测量法测定材料在动态拉伸[28,109]、压缩[24, 50, 110]、扭转[26, 28, 103, 105, 108]、压剪[32, 112–113]、帽型剪切[111]和靶板冲击[106–107]等加载条件下表面剪切带及其附近区域的温度演化，相关研究结果总结于表3。测试设备除了常见的红外测温传感器，还有高精度热像仪[108]和高速红外相机[109]等，测温原理基本相同。其中，红外测温传感器采用多种探元组合形式，包括单个探元[28,110,115]、单列探元（探元数目分别为3[32]、8 个[112]、10[104]、12[28,103]、16[106]）和矩形阵列[107,116]等。探元的排布满足了对被测试样沿不同方向、不同位置处温度的测量需求，也使人们对绝热剪切带及其周围区域的温度演化有了更全面的了解。

事实上，还有学者同时采用接触式热电偶测量法和非接触式红外测量法研究了聚合物材料动态变形过程中的绝热温升，并对测试结果进行了对比分析。Regev 等[117]以PC 高分子聚合物为研究对象，使用T 型热电偶和红外探测器对其在SHPB 动态加载过程中试样中心和表面的温度变化进行了原位同步测量。图16(a)和图16(b)为加载应变率分别为3 000 s−1和6 000 s−1时试样应力和温度随应变的变化，可以看出试样内部（黑色实线）和表面（红色虚线）的温升基本重合，从而验证了其测温方法的有效性。Kendall 等[92]采用两个试样夹住热电偶丝或热电偶薄片的方法测量聚合物在SHPB 加载过程中的温升，并与传统钻孔式内嵌热电偶和红外热像仪测温方法进行了比较，发现改进的热电偶薄片夹芯测试方法具有以下优点：与红外热像仪法相比，可以测试材料中心的温度，且温度测试结果更精确；与钻孔式内嵌热电偶测试方法相比，没有改变试样结构，被测试材料的力学行为未受到影响。

表3 绝热温升实验测量结果Table 3 Previous measurements of adiabatic temperature rise

图16 PC 高分子聚合物在3 000 s−1（a）和6 000 s−1（b）应变率下应力和温度随应变的变化曲线（蓝色实线为真实应力，黑色实线为热电偶测温结果，红色虚线为红外测温结果。）[117]Fig. 16 Typical stress-strain-temperature plot at 3 000 s−1 (a) and 6 000 s−1 (b) （The blue solid line represents the real stress, the black solid line represents the thermocouple temperature measurement results, the red dotted line represents the infrared temperature measurement results.）[117]

本节介绍了热电偶测量法和红外测量法两种绝热温升的原位测量方法。经过多年的发展，两种测试方法已日趋成熟，并应用于各种极端条件下热力耦合问题的实验测试之中。然而，微观观测发现，绝热剪切带宽度往往在数微米尺度，有的甚至在纳米尺度，无论是热电偶工作端的尺寸还是红外测温设备中探元的尺寸，目前还无法达到这一水平。尽管Duffy 等[103,105]通过在探元和试样之间设置放大光路将探元在试样上测试区域的边长缩小到17 µm，但却因此缩小了测温区域的范围，导致常常难以测到最大的温升位置，也增加了实验操作的难度，并且仍然无法直接测量宽度更小的剪切带内温升。因此，实验所得的温度是试样表面某个区域内的平均温度，对于剪切带宽度小于探元尺寸的温度测量不够精确，其实验结果往往偏小。除此之外，非接触式红外测温法只能测得试样表面温升的演化，无法得知试样内部的温度分布。尤其对于某些压剪试样等变截面试样，试样表面和内部的应力状态和变形程度不同，因此测得的结果也可能会有偏差。

4 微观组织与温度升高

在原位测温技术出现之前，往往通过试样动态加载后的微观形貌间接推测材料的温升历史，借助各种微观表征方法，观察绝热剪切带内的微观结构，并结合理论计算讨论温升在材料绝热剪切过程中的作用。

Zener 等[7]在钢的高速穿孔实验中观察到了白色亮带，结合硬度测试结果推测其产生的原因是剪切带内发生了从高温迅速降温的淬火过程，并估算出应变为5 时对应的带内温升已达1000 K。Giovanola[118]通过扫描电子显微镜（SEM）对4340 钢动态扭转加载后材料断面的微观形貌进行了表征。图17(a)显示了材料断面的整体形貌，可以看到斑状的微孔洞区域和瘤状凸起（Knobbles）。图17(b)是瘤状凸起处的放大图，可以看到材料表面被瘤状凸起附着，并且右下角有微孔洞被拉长的痕迹。根据该形貌特征推断，材料发生大剪切变形时产生了大量的热，导致材料出现明显的局部温升。

图17 绝热剪切的微观形貌[118]：（a）4340 钢动态扭转加载后材料断面的整体微观形貌，（b）瘤状凸起处的放大图Fig. 17 Microstructure of adiabatic shear[118]: (a) microstructure of cross section of 4340 steel after dynamic torsion loading, (b) higher magnification SEM fractograph of the knobbly region

Marchand 等[103]对HY-100 结构钢动态扭转后的断口形貌进行了表征，在硝酸酒精溶液处理后的断口处观察到了白色侵蚀面，据此推测该区域在塑性变形过程中发生了相变，如图18(a)所示。Me-bar 等[4]采用透射电子显微镜（TEM）对Ti-6Al-4V 靶板冲击后剪切带内的微观组织进行了表征，如图18(b)所示。可以看到非常细的晶粒组织，并据此推断剪切带内的温度已经达到了Ti-6Al-4V 的 β转变点，对应的温升达950 K。但是可能由于带内温度还未达到熔点或高温持续时间过短，导致残存了一些片晶组织。此外，高应变率加载条件下试样出现的绝热温升为再结晶提供了有利条件。Nemat-Nasser 等[119]采用背散射电子技术观察单晶铜动态压缩后的试样切面，在微观图像中同时观察到了再结晶晶粒和裂纹，并将塑性变形产热引起的剧烈温升视为再结晶产生的原因之一。

许多学者对不同材料绝热剪切过程中出现的再结晶现象进行了深入研究。Andrade 等[120]对金属铜帽型试样进行了动态剪切加载，以104s−1应变率加载至剪切应变为5 时剪切带内部的TEM 微观结构和选区衍射情况如图19(a)所示。可以看出，剪切带内出现了大量新晶粒，即再结晶现象。采用功热转化法估算此时剪切带内的温度超过600 K，高于铜发生再结晶的温度（523 K），由此推断再结晶是该金属发生绝热剪切的重要机制之一。此外，Meyers 等[121]还观察到钛、铝-锂合金和钽动态加载后剪切带内发现了再结晶现象，并首次提出了晶粒转动在材料变形过程中的重要作用。其中，在8090 铝-锂合金剪切带内部发现了大量平均直径为0.2 µm 的等轴晶粒[122]，如图19(b)所示，从其衍射图谱可以看出这些晶粒的取向分布较为均匀。值得注意的是，并没有观察到沉淀物，也说明剪切带内部的温度超过了该合金的固熔线（500 ℃）。

图18 （a）HY-100 结构钢动态扭转加载后断面的白色侵蚀面[103]，（b）Ti-6Al-4V 靶板冲击后剪切带内的微观组织形貌[4]Fig. 18 (a) White erosion surface of HY-100 structural steel after dynamic torsion loading[103],(b) microstructure in shear band of Ti-6Al-4V target after impact[4]

图19 （a）铜剪切带内部的TEM 微观结构和衍射图谱[120]，（b）8090 铝-锂合金剪切带内部的TEM 微观结构和衍射图谱[122]Fig. 19 (a) TEM microstructure and diffraction pattern of copper shear band[120], (b) TEM microstructure and diffraction pattern in shear band of 8090 Al-Li alloy[122]

Hwang 等[123]通过SEM 观察等径通道角挤压法（ECAP）制备的超细晶低碳钢动态扭转加载后的微观形貌，发现剪切带内有细化的球状化渗碳体，推测剪切带内的温升至少达到了540 K，这也解释了铁素体处晶粒出现的再结晶现象。Meyers 等[48]对比了304 不锈钢帽型试样动态加载后剪切带内和带外的晶粒形貌，其微观TEM 形貌如图20(a)和图20(b)所示。从图20(a)中可以看到剪切带内的晶粒尺寸为50～100 nm，图20(b)中剪切带外原始晶粒的平均尺寸为30 µm，并且原始晶粒内部存在大量位错，将这种剪切带内纳米级尺寸晶粒的出现归因于旋转动态再结晶（Rotational recrystallization）机制，区别于迁移动态再结晶（Migrational recrystallization）。此外，他们还利用功热转化关系估算了剪切带内的理论温升，计算结果显示剪切带内的温升近900 K，接近不锈钢的熔点，这种剧烈温升对其最终微观结构的形成产生了重要影响。Jiang 等[42]对ZK60 镁合金动态加载后剪切带附近的微观形貌进行了TEM 表征，如图20(c)所示。蓝色虚线为剪切带边界，①、②和③分别对应剪切带外、剪切带边缘和剪切带内的选区衍射图。通过对比可以看出，剪切带内形成了取向差异明显的再结晶晶粒，剪切带边缘则处于过渡区。通过功热转化关系计算了图中应变状态下剪切带内的理论温度为663 K，高于ZK60 镁合金的动态再结晶温度（454 K），为动态再结晶的形成创造了有利条件。

图20 不锈钢动态加载后的微观TEM 图[48]：（a）剪切带内形貌，（b）剪切带外形貌，（c）ZK60 镁合金剪切带及其附近的微观形貌和不同位置的选区衍射图[42]Fig. 20 TEM micrograph of stainless steel after dynamic loading [48]: (a) microcrystalline structure inside bands, (b) large grains outside bands, (c) bright field image and selected area diffraction (SAD) pattern of the ZK60 magnesium alloy microstructure in shear region[42]

Lins 等[46]对无间隙原子钢（IF 钢）帽型试样动态加载后的微观形貌进行表征。图21(a)是利用电子背散射衍射（EBSD）技术得到的剪切带附近晶粒的形貌及取向分布图。可以看出，剪切带内形成了大量等轴的再结晶晶粒，计算得到剪切带内的理论温升可达1 000 K，这对材料的再结晶与回复有着重要影响。Liu 等[124–125]对某种钛合金（Gum metal）分别进行挤出（Extrusion）和等径通道角挤压（ECAP）的晶粒细化处理，并研究其在动态加载条件下绝热剪切带的微观演化和形成机制。图21(b)为ECAP 晶粒细化钛合金试样加载后剪切带及其附近区域的晶粒形貌和取向分布。与带外相比，剪切带内形成了大量超细晶等轴晶粒，推断动态加载时剪切带内产生了剧烈温升。此外，通过理论计算得到了两种材料绝热剪切带产生之前的温升，发现其中挤出钛合金的温升不足以触发再结晶，据此提出产生绝热剪切带的原因是材料在低温大变形条件下的微观结构软化效应。

图21 （a）钢中剪切带及其附近区域的晶粒形貌及取向分布[46]，（b）ECAP 晶粒细化处理钛合金中剪切带及其附近区域微观形貌及取向分布[124]Fig. 21 (a) Grain morphology and orientation distribution of shear band and its vicinity in steel[46], (b) microstructure and orientation distribution of shear band and its vicinity in ECAP grain refinement titanium alloy[124]

以上研究结果表明，许多材料的绝热剪切带中都存在再结晶现象，大量研究将再结晶与绝热剪切温升联系起来，认为温升是造成材料再结晶的原因之一，并推测再结晶也是绝热剪切带形成的一种微观机制。值得注意的是，以上观测均是在绝热剪切带形成后的材料中进行的，即再结晶和绝热剪切带具有伴生关系，但是对于再结晶与绝热剪切带产生的因果联系仍未给出明确阐述，即并没有回答再结晶是产生绝热剪切失效的原因还是其导致的结果。Rittel 等[126]对Ti-6Al-4V 压剪试样进行限制应变的单次加载，并用TEM 观察试样的微观形貌。他们发现，在剪切带形成之前的试样内部形成了尺寸为10～30 nm 的动态再结晶晶粒，如图22(a)中黑色箭头指向的晶粒，从其选区衍射图中也可以看到取向均匀的纳米多晶结构。由此可以说明，动态再结晶过程早于绝热剪切带的形成，而此时材料未出现明显的变形局部化，因此温升仍处于较低水平且在试样均匀分布，可以忽略局部大变形和温升对再结晶过程的影响。Liu 等[124]对经ECAP 处理后的钛合金进行了动态加载，图22(b)和图22(c)是试样加载后的整体和局部形貌。在绝热剪切带尚未完全形成之前的试样表面发现了大量动态再结晶形成的等轴晶粒，此时材料的整体温升可能只有几十摄氏度，与Rittel 等[126]的实验结果类似。以上结论与Guo 等[112]关于温升与绝热剪切带形成之间因果关系的讨论一致，即温升很有可能是剪切带产生的结果。

图22 绝热剪切带产生之前Ti-6Al-4V 试样内出现的再结晶晶粒及其对应的选区衍射图[126]（a）；钛合金试样剪切带完全形成前试样的整体（b）和局部（c）形貌[124]Fig. 22 Recrystallized grains in Ti-6Al-4V before adiabatic shear band and their corresponding selected area diffraction patterns[126] (a); whole (b) and microstructure (c) of the shear band morphology for ECAP titanium alloy[124]

综上所述，动态加载后的微观观察是了解材料绝热剪切过程中形貌演化和温升历史的有效手段，也是揭示绝热剪切带产生机理的重要方法。但就像Nieto-Fuentes 等[58]对绝热剪切过程中能量转化研究的结论一样，某些物理现象及其内在机制的研究很大程度上依赖于对整个过程的了解，仅靠初、终态的研究是不够的。因此，该部分内容的研究往往需要结合其他手段，例如实验测量、理论计算、模型仿真等。将多个研究角度相结合会帮助我们更接近绝热剪切的“真相”。

5 总结与展望

本文从理论计算、数值方法、实验测量和微观组织4 个方面对绝热剪切中温升的研究进行了总结和讨论。具体内容包括：理论计算中基于功热转化的温升估算和剪切带及附近温度场计算，数值模拟中一维热传导理论、热力耦合方法和有限元法对温升的计算，实验测量中热电偶测量法和红外测量法对温升的直接测量以及微观组织变化间接反映的温升历史。希望通过本文的总结，对后续相关领域的研究产生一定的启发，对绝热剪切现象的深入研究提供有用的参考。

通过对已有文献的整理可以看出，虽然绝热剪切现象及其中的温升研究取得了很大进展，但是仍存在一些尚未完全解决的问题，进一步研究和解决这些问题将对绝热剪切失稳以及材料动态失效理论的发展起到重要的推动作用。未来包括研究方向：

（1）功热转化现象的深入研究。如功热转化系数与哪些因素相关，外力功除转化为热能之外还转化成了哪些形式的能量，这些能量是存储在材料中还是以某种形式耗散掉，热能以及储能中缺陷、残余应力状态等各占多大比例。

（2）研制高分辨率测温仪器。此处的高分辨率包括高时间分辨率（响应时间低于1 µs）和高空间分辨率（探元尺寸在微米量级），只有这样才能够精确测量绝热剪切带形成过程中的温度。同时，该仪器还可用于动态断裂等领域的温度测量。

（3）绝热剪切带的形成机制。热塑性失稳机制是多数学者认可的绝热剪切带形成机制，然而近年来该机制也受到了质疑与挑战，关于温升在绝热剪切带形成过程中的作用仍存争议。诸多学者提出了如晶粒转动、再结晶、微观损伤等触发绝热剪切失稳的新机制，而何种机制主导了绝热剪切带的形成亦或是哪几种机制的共同作用值得进一步探讨。