冲击载荷下Ni52Ti48 合金的微观响应特性
2021-07-25张旭平王桂吉罗斌强吴恒安谭福利赵剑衡刘仓理孙承纬
吕 超,张旭平,王桂吉,罗斌强,罗 宁,吴恒安,谭福利,赵剑衡,刘仓理,孙承纬
(1. 中国科学技术大学近代力学系,中国科学院材料力学行为和设计重点实验室,安徽 合肥 230027;2. 中国工程物理研究院流体物理研究所,四川 绵阳 621999;3. 中国矿业大学力学与建筑工程学院深部岩土力学与地下工程国家重点实验室,江苏 徐州 221116;4. 中国工程物理研究院应用电子学研究所,四川 绵阳 621999;5. 中国工程物理研究院,四川 绵阳 621999)
形状记忆合金(Shape memory alloys,SMA)的基本特征是具有在适当的外部刺激下可恢复变形前形状的能力,并保持较大的可逆变形(通常为5%~10%)[1],前一个特性称为“形状记忆效应”,后者称为“超弹性或拟弹性”。尽管已发现大量的SMA,但NiTi(Nitinol)是当前研究最多的材料之一,并且在最近的大多数应用中均被列为首选[2]。这主要是由于NiTi 具有诸多出色的特性,如生物相容性、高耐腐蚀性和耐磨性等[3–6]。NiTi 合金常用于航空致动器、地震测试设备、卫星和太空飞行器的保护结构或关键部件。在这些应用中,NiTi 合金器件经常面临诸如高速飞行物撞击等高压、高应变率的极端环境[7–8],因此深入认识高压和高应变率下NiTi 合金的动力学响应具有重要的科学意义和工程应用价值。
目前唯象经验的Johnson-Cook 本构模型已被用于描述斜波和冲击加载下NiTi 的动力学响应行为[9],能较好地反映动载荷下的宏观响应特征,但是无法有效描述高压高应变率下物体变形的微结构特征。亟需从材料微观变形出发,构建基于微结构物理机制的NiTi 本构模型,以获取高压高应变率下NiTi 的微观变形机制。高压高应变率下NiTi 的微观变形研究包括奥氏体-马氏体相变和以位错、孪晶为主的塑性变形。20 世纪90 年代以来,围绕应力诱导的马氏体相变的应变率敏感特性,材料科学、力学以及凝聚态物理领域的研究者们开始关注动载荷下NiTi 合金的物理力学性质。一般认为,随着应变率的增加,相转变速率会趋于极限,即应力诱发的奥氏体向马氏体相转变阶段在应变率超过6000 s−1时基本不变,表明更高的应变率不能引起NiTi 相变转换;在6000 s−1以下,先出现马氏体相变,后出现马氏体的塑性屈服,高于临界应变率时,变形为母相奥氏体的位错诱导的塑性变形[10–14]。2017 年本课题组通过磁驱动高速飞片实验结合数值模拟证明了奥氏体Ni52Ti48在104~107s−1的冲击压缩应变率区间没有发生相变,并将该结果与此前研究结果的较大差异归因于NiTi 合金的相变受组分含量的影响较大[9],这也是本文第2 节的主要内容。
得益于严格的电子显微镜研究,实验上已经基本确定了NiTi 的位错滑移结构以及主要的滑移系,基于密度泛函理论(DFT)的临界剪切应力预测也与实验测量值基本吻合。一般认为,当缺乏容易激活的独立滑移系时,孪晶作为另一种基本的塑性变形模式就会产生。在NiTi 马氏体中,存在3 种类型的孪晶:Ⅰ型、Ⅱ型和混合孪晶。孪晶的产生包括成核和生长,成核应力远大于生长应力,而孪晶的成核易受众多内部和外部因素的影响,包括组分、晶粒尺寸、温度和应变率等[15],意味着强冲击加载环境下NiTi 的孪晶模式可能与常压下存在很大的不同,理解高压高应变率下NiTi 的孪晶模式有利于准确预测极端环境下孪晶的临界剪切应力。探索高压高应变率下NiTi 的位错、孪晶等微结构的动力学演化过程具有重要的科学意义,原子空间尺度分子动力学方法常被用于阐明原子尺度下NiTi 的微结构演化过程。Yin 等[16]使用Zhong 等[17]的改进势函数,发现随着初始环境温度的升高,一维应力下单晶NiTi 的冲击变形模式由相变/孪晶转变为单一的位错运动。Yazdandoost 等[18]进一步研究了局部冲击荷载下单晶和多晶材料的冲击行为与能量耗散的关系,基于应变提出了检测相变和塑性变形的判据,还考虑了晶粒尺寸和晶界类型的影响。Wang 等[19]利用Ko 开发的MEAM 势函数,研究了单晶NiTi 在一维应变冲击加载条件下的动态响应,包括孪晶、相变、退孪晶等行为。目前这些研究多限于单晶样品,加载条件较单一。基于上述模拟研究现状及2017 年本课题组的实验工作,2020 年我们进一步开展了不同冲击加载速度和初始环境温度下Ni52Ti48合金的微结构演化特征和变形机制研究,试图对实验工作给予一定的解释[20]。该模拟工作与实验工作一同在第2 节中进行介绍,第3 节探讨了冲击加-卸载拉伸下Ni52Ti48合金的层裂强度随初始温度和冲击速度的演化关系。相关研究结果对深入认识Ni52Ti48合金的动力学特性具有重要的科学意义,也有助于其在一些极端服役环境下的应用。
1 材料准备及实验和模拟方法介绍
实验样品为近等原子比Ni52Ti48合金,由中国西北形状记忆合金公司提供,材料的基本数据见表1[9],其中: ρ为密度,CLO为纵向声速,Cs为剪切声速,Cb为体声速, ν为泊松比,TMs为马氏体的起始相变温度,TMf为马氏体的最终相变温度,TAs为奥氏体的起始相变温度,TAf为奥氏体的最终相变温度。图1 为电子背散射衍射(Electron backscattered diffraction,EBSD)微观表征结果,可以看出,实验样品没有明显的择优取向,取向较分散,平均晶粒尺寸约为35 μm。实验中NiTi 合金样品的初始平面度约1 μm,光洁度约20 nm,通过飞片和样品的精加工,控制初始飞片与样品撞击表面的平行度为3 μm左右。

表1 实验用NiTi 合金材料的基本数据[9]Table 1 Characteristics of as-received NiTi alloy[9]
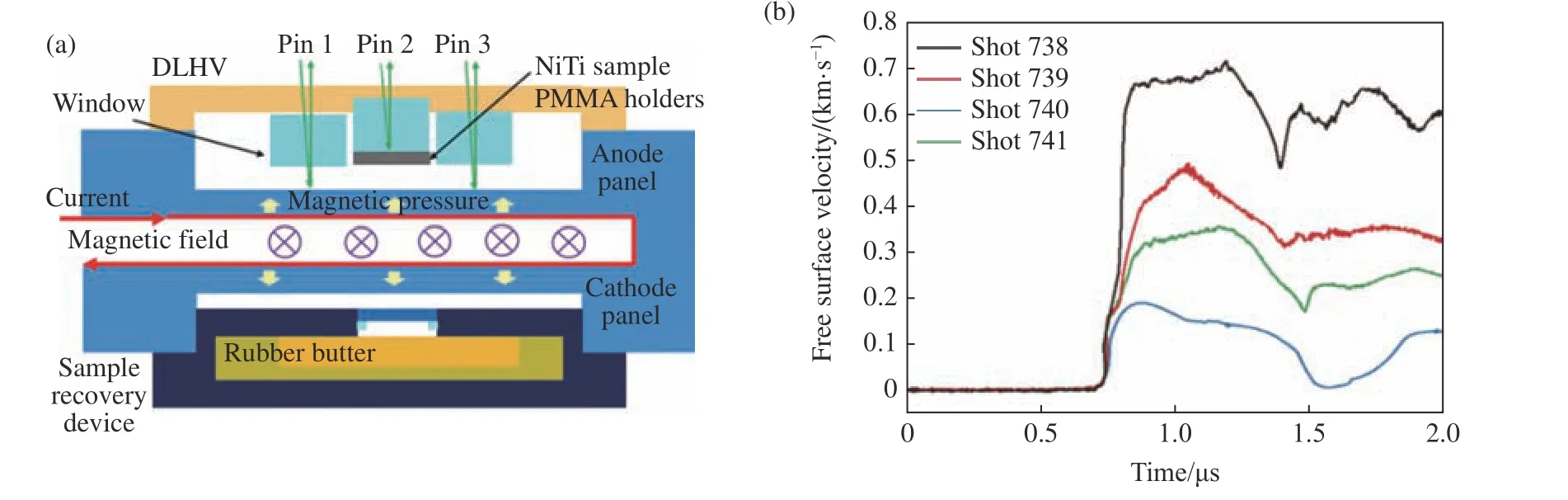
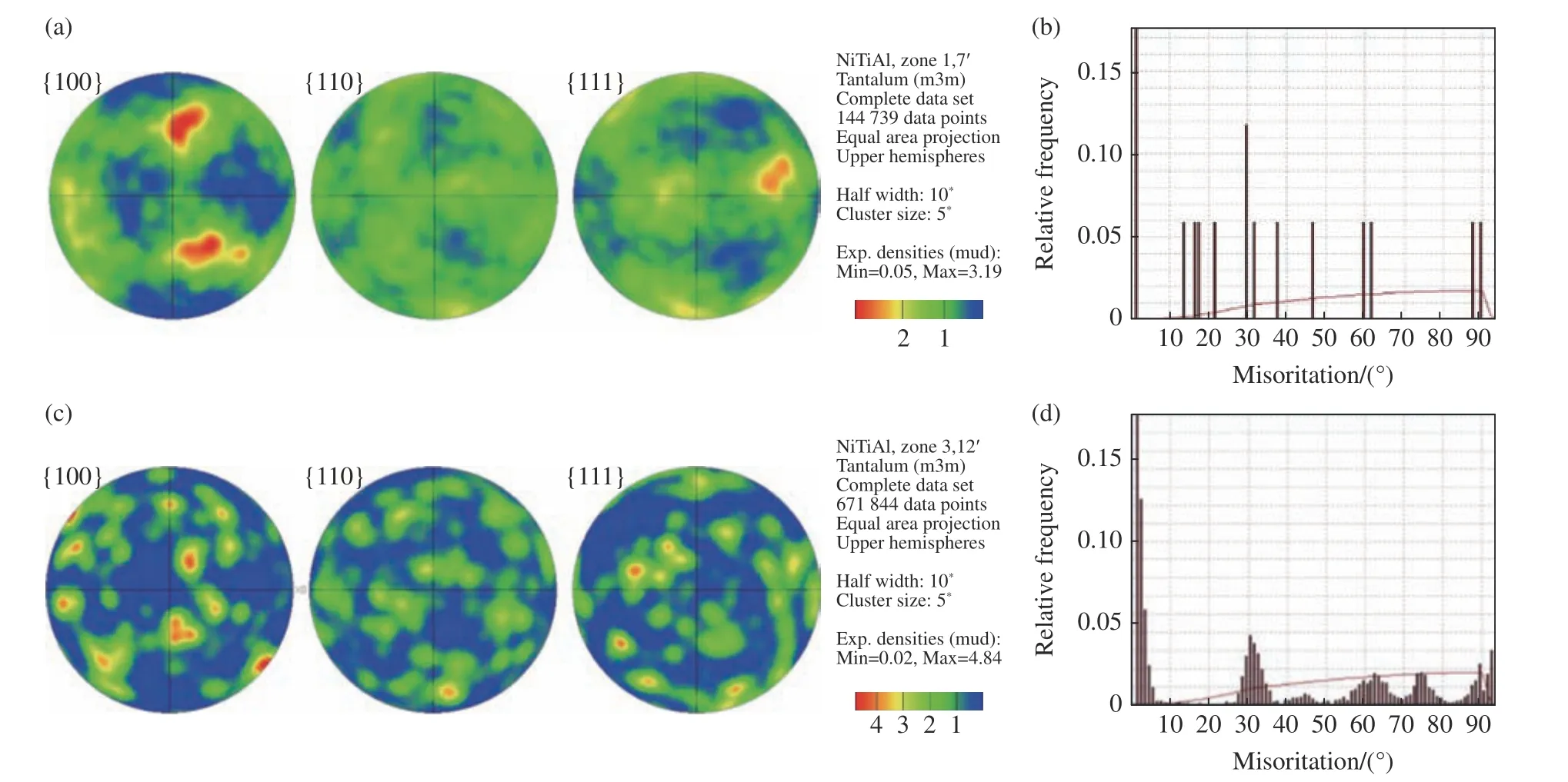
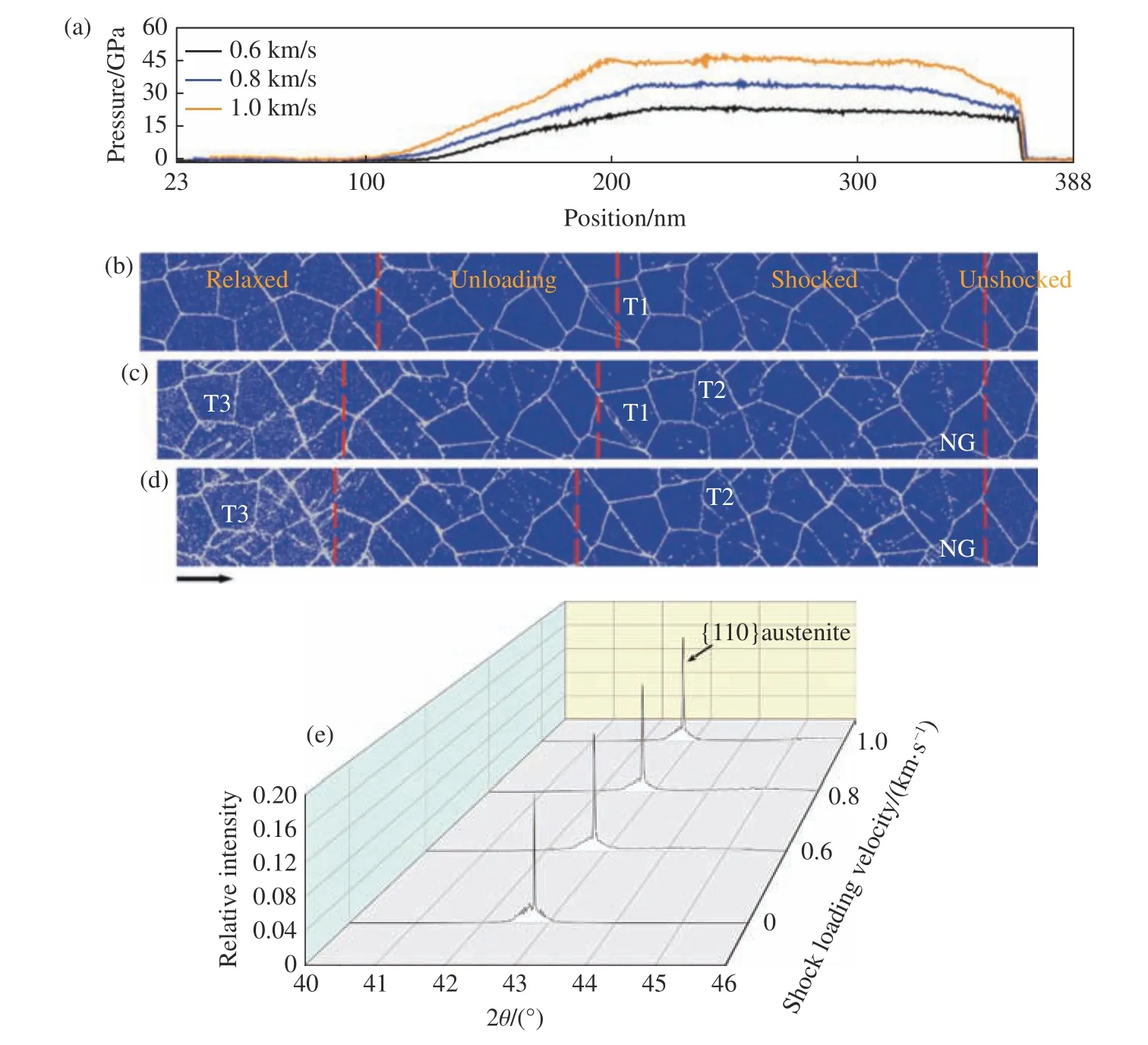
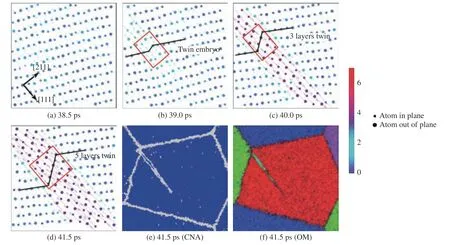
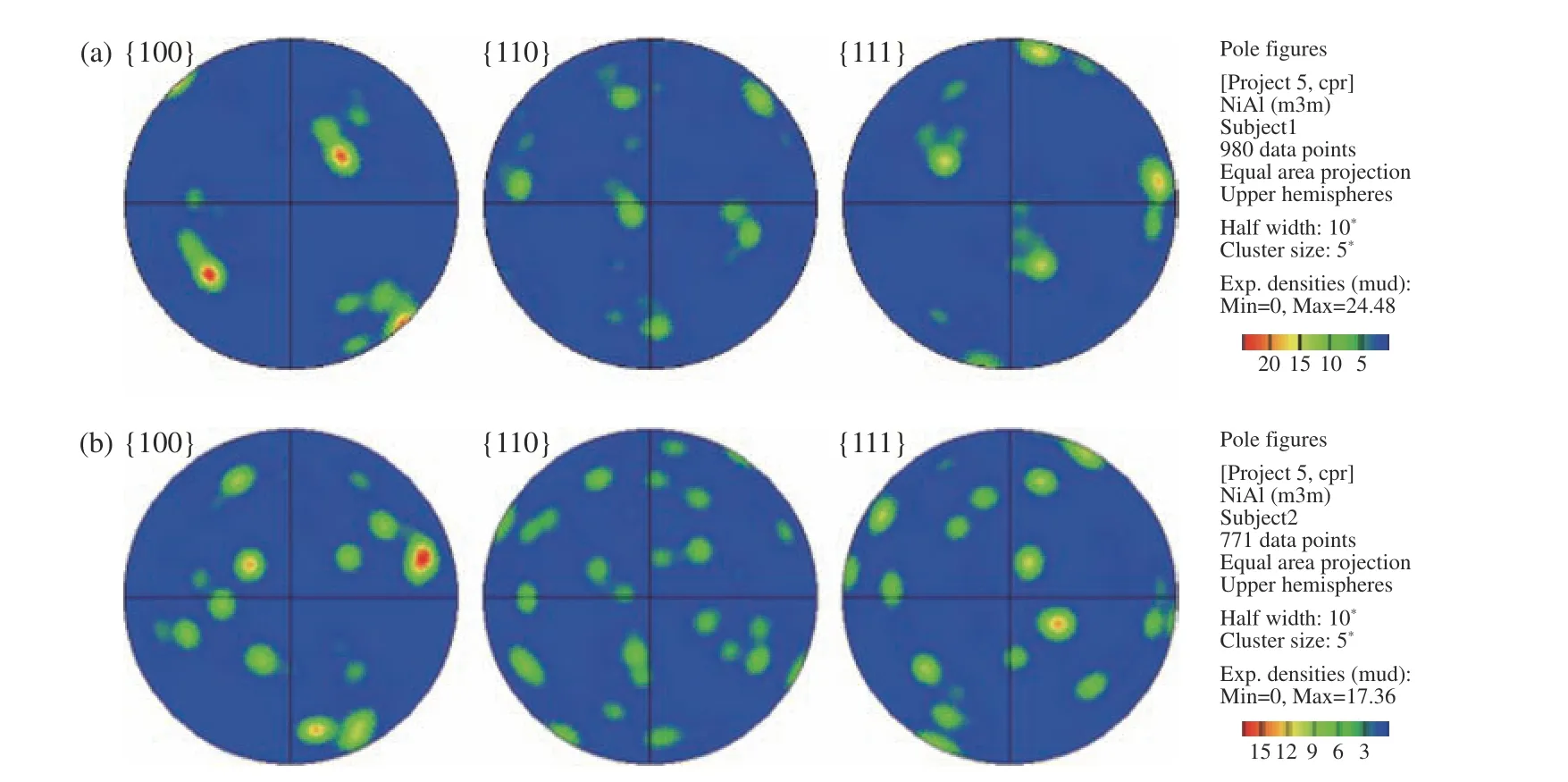
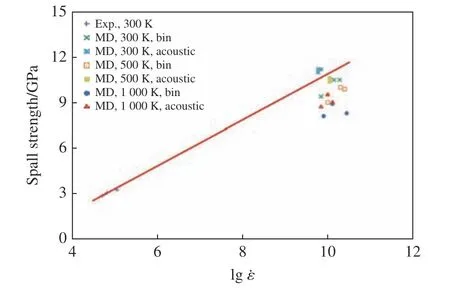
冲击压缩和冲击压缩-卸载拉伸实验都在大电流脉冲功率装置CQ-4 上进行[21–22]。平板冲击压缩实验原理和平板冲击压缩实验的典型速度曲线分别如图2(a)和图2(b)所示。冲击压缩实验中,为了避免冲击加载下边侧稀疏波在反射后向样品内部传播,依据阻抗匹配原则,采用与NiTi 样品波阻抗接近的铜作为动量陷阱进行冲击压缩后的样品回收,以捕获动量并衰减加载应力波,实现了NiTi 样品的回收。速度波剖面均呈现出明显的双波结构,样品经历了典型的弹塑性转变。Ni52Ti48合金的冲击雨贡纽关系为D= 4.351 + 1.588u(0.1 km/s 图1 EBSD 测得的Ni52Ti48 合金显微组织的反极图(a)[9]、取向分布散点图(b)及取向分布密度图(c)Fig. 1 Inverse polo figure (IPF) map[9] (a), scatter diagrams (b) and contour map (c) of as-received polycrystalline NiTi samples measured by EBSD 图2 电磁驱动平板冲击压缩实验原理(a)及平板冲击压缩实验典型速度曲线(b)[9]Fig. 2 Schematic of magnetically driven planar shock experiments (a) and typical velocity profiles of shock wave experiments (b)[9] 图3 电磁驱动平板冲击压缩-卸载拉伸实验原理(a)及样品自由面速度历史(b)[23]Fig. 3 Schematic of magnetically driven planar shock compression and unloading tensile experiments (a)and the free surface velocity profiles of samples (b)[23] 非平衡分子动力学模拟(Non-equilibrium molecular dynamics simulation,NEMD)在大规模原子分子大规模并行模拟器(Large-scale atomic molecular massively parallel simulators, LAMMPS)上开展[24]。采用Lai 等开发并经Zhong 等改进的嵌入式原子方法(EAM)势[17,25],该势较好地描述了静态压缩/拉伸下NiTi 的力学性能与微观结构之间的关系。对于温度变化引起的NiTi 相变也有合理的解释,高应变率冲击载荷下该势的适用性和可靠性验证工作详见文献[20]。 利用动量陷阱回收技术,有效回收了冲击压缩下的Ni52Ti48合金样品,结合X 射线衍射(X-ray diffraction,XRD)和EBSD 金相显微分析技术,对样品进行了微观特性表征。尽管应力诱发的马氏体转变在释放时是可逆的,但是在回收样品中仍可观察到一些马氏体的残存结构。图4 和图5 所示的XRD 和EBSD 分析结果均未观察到马氏体结构,表明冲击压缩后样品没有发生奥氏体至马氏体转变,而是发生了弹塑性转变,与图2(b)给出的宏观速度波剖面结果一致。 退火后的初始NiTi 样品(见图1(a))为晶粒分布均匀的典型等轴晶组织,无明显织构化组织,平均晶粒尺寸为30~40 μm 。经平板冲击压缩加载后,在Ni52Ti48合金内部除了形成大角度晶界,还产生了高密度的小角度晶界,它由高密度位错组织结合而成,包含位错缠结、位错墙等,如图5(a)所示。回收的Ni52Ti48样品中产生了变形孪晶和再结晶,变形孪晶和再结晶在特定区域内同时存在,再结晶颗粒在晶粒内部均匀分布,这可能是由温度效应引起的,也可能是由变形孪晶成长形成。 图4 初始和实验回收多晶NiTi 样品的XRD 谱[9]Fig. 4 XRD patterns of as-received and experimentally recovered polycrystalline NiTi samples[9] 图5 冲击加载速度up = 0.927 km/s 时冲击压缩回收NiTi 样品的反极图(a)以及孪晶(b)和再结晶(c)的局部放大图Fig. 5 (a) EBSD characterizations of experimentally recovered polycrystalline NiTi samples at shock loading velocity up = 0.927 km/s at room temperature, and the corresponding amplified configurations in (a),which represent (b) twins and (c) re-crystalline, respectively 图6(a)所示的反极图(IPF)显示,代表不同取向的点分布得比较分散,没有主要的分布颜色,证明所测区域无择优取向。图6(b)中y0、z0方向的晶向分布比较均匀,而x0方向的反极图中晶向略有集中,最强极密度强度为2.25,与图1(b)和图1(c)对比表明,NiTi 合金经冲击压缩加载后没有发生非常强烈的择优取向,取向除x0方向外依然较分散。 图6 冲击压缩加载下NiTi 样品在横向(x0)、纵向(y0)和法向(z0)的取向分布散点图(a)和取向分布密度图(b)Fig. 6 IPF distribution of horizontal (x0), longitudinal (y0) and normal (z0) direction of NiTi under shock compression: (a) scatter diagrams, (b) contour map 图7 是经分析软件处理得到的初始NiTi 合金样品和冲击加载后回收样品的{001}、{011}和{111}极图。冲击压缩加载后回收样品的极图颜色对比较明显,密度强度相差较大,蓝色低密度强度面积占比较大,在{001}极图中存在最高密度强度,最高密度强度为4.84。而初始NiTi 合金样品的极图中,绿色低密度强度面积占比较大,在{001}极图中存在最高密度强度,最高密度强度为3.19。这表明冲击压缩加载后回收样品所选区域中晶向的规律性比初始样品强。 图7 NiTi 合金初始样品(a)和冲击压缩回收样品(c)的极射赤面(赤道面)投影图及其对应的晶界角度分布(b, d)Fig. 7 Pole figures (equatorial plane) of NiTi: (a) as-received and (c) recovered samples under shock compression;(b) and (d): the histograms of frequency and distribution of the boundaries for (a) and (c), respectively 初始样品和冲击压缩回收样品内部晶界分布如图7(c)和图7(d)所示。可见,小角度晶界比例明显上升,晶界取向小于10°的小角度晶界明显增多,与EBSD 表征结果吻合,说明材料经历了明显的塑性变形。此外,图7(b)和图7(d)所示的初始样品和变形回收样品的晶界角度频率分布直方图显示,变形回收样品中产生了约70.5°的新晶界类型,结合图4 中的XRD 分析结果,可以认为产生的是{112}奥氏体孪晶。这说明在B2 奥氏体近等原子NiTi 的冲击压缩实验中没有产生马氏体相,高应变率下的变形方式为塑性变形,包括位错、孪晶、新晶粒等。 为了解释实验中所观察到的孪晶和再结晶现象,采用分子动力学模拟研究了其可能机理。图8 显示了在环境温度300 K 下以不同冲击粒子速度up(0.6、0.8 和1.0 km/s)冲击压缩时nc-NiTi 的NEMD模拟结果。随着冲击波(持续时间35 ps)的传播,nc-NiTi 中存在多种应力状态,在图8(b)~图8(d)中用红色虚线区分,标记为Relaxed、Unloading、Shocked 和Unshocked。在整个模拟过程中,没有发生相变,与实验结果一致。NiTi 样品的宏观冲击实验和微观NEMD 冲击模拟显示出非常相似的塑性变形特性,模拟中生成的所有孪晶均为{112}类型,与实验结果一致。为方便起见,在nc-NiTi 的NEMD 模拟中将处于3 个不同位置和阶段的孪晶标记为T1、T2 和T3,NG 表示在冲击载荷下形成的新晶粒。 图8 不同冲击粒子速度下的一维应力波剖面演化(a);不同冲击粒子速度下的演化结果比较:(b) 0.6 km/s,(c) 0.8 km/s,(d) 1.0 km/s(不同的状态以红色长划线区分,微结构包括孪晶T1、T2、T3 和新晶粒(NG),用CNA 方法进行表征,冲击方向用黑色箭头标示);初始奥氏体以及图8(b)、图8(c)和图8(d)所示nc-NiTi 模型的模拟XRD 分析结果(e)[20]Fig. 8 (a) 1D pressure profiles in nc-NiTi under different shock-loading velocities; comparisons of simulated results corresponding to (a) at initial ambient temperature 300 K and different loading velocities: (b) 0.6 km/s, (c) 0.8 km/s,(d) 1.0 km/s (Different states are distinguished by red long dashes. The microstructures are characterized by CNA methods: twin T1, T2, T3 and new grain (NG). The shock direction is labelled by black arrows.); the simulated XRD patterns (e) of the nc-NiTi models for initial austenite, Fig.8(b), Fig.8(c) and Fig.8(d), respectively[20] 2.2.1 三晶界附近变形模式的冲击载荷速度依赖性 图9 nc-NiTi {112}奥氏体孪晶T1 在冲击速度up = 0.6 km/s 下的成核和扩展[20]Fig. 9 Nucleation and growth of {112} twin T1 in austenite phase at shock loading velocity up = 0.6 km/s for nc-NiTi[20] 图10 在up = 0.6 km/s 和up = 0.8 km/s 两种情况下孪晶和位错的竞争机制[20]Fig. 10 Competition mechanism of twins and dislocations at up = 0.6 km/s and up = 0.8 km/s[20] 与up= 0.6 km/s 和up= 0.8 km/s 的情况不同,up= 1.0 km/s 时三叉晶界处产生了非晶剪切带而非孪晶,如图11 所示。这是由于当冲击波通过三叉晶界时,在该区域(27.5 ps)积累局部应力。当超过孪晶(和位错)模式的应变适应能力时,会导致来自三叉晶界处的非晶剪切带成核(35.0 ps)[30]。径向分布函数(RDF)计算验证了在上述区域中产生了非晶态结构。 图11 up = 1.0 km/s 时三叉晶界处形成的非晶剪切带以及B2 结构的sc-NiTi 和nc-NiTi 中非晶剪切带的径向分布函数g(r)[20]Fig. 11 Formation of amorphous shear band at grain boundaries (GBs) triple junction for shock loading velocity up = 1.0 km/s,and the radical distribution function g(r) of the B2 structure sc-NiTi and amorphous shear band in nc-NiTi[20] 2.2.2 纳米级旋转变形导致nc-NiTi 中产生新晶粒 利用分子动力学模拟对新晶粒的产生进行了解释。如图12(a)所示,原晶粒(Parental grain,PG)由大角度晶界(Large angle grain boundary,LAGB)和小角度晶界(Small angle grain boundary,SAGB)构成。up= 0.8 km/s 时,冲击波通过该区域后,在大角度晶界和小角度晶界处都发生了纳米级的集体理想剪切。这会导致从大角度晶界激发出的相同{112}<111>滑移系统(以及具有{110}<100>滑移系统的小角度晶界)激发出若干位错,并且相邻位错滑移面之间的距离大约只有两个晶格宽度。 如图12(b)所示,在位错滑行区域中产生了纳米扰动壁,它由具有很小的伯氏向量 ±b(小于相应的全位错,如a<111>、a<100>)的非晶体位错组成。纳米扰动壁会引起该区域的旋转变形。当b的大小增加到完全位错b0时,纳米扰动壁最终消失,并且对应于平行位错的整个区域完成旋转。考虑到原晶粒的大角度晶界和小角度晶界都朝向晶粒内部发出位错,因此从大角度晶界和小角度晶界发出的位错滑移系是不同的,这些位错在原晶粒内部相遇并发生相互作用,从而阻碍位错的传播,并在位错相互作用区域产生晶界,形成新的晶粒[31]。用OM 方法可以更清楚地识别出新晶粒的形成过程,新晶粒的取向与原晶粒明显不同。图12(g)~图12(h)显示了纳米旋转变形产生的新晶粒的原理。 基于CQ-4 装置,利用平板冲击加-卸载拉伸实验和样品软回收实验技术,开展了不同加载压力下Ni52Ti48的层裂强度测量,实验原理如图3(a)所示,利用DLHV 测得的样品自由面速度剖面如图3(b)所示。据此进一步处理得到Ni52Ti48合金的Hugoniot 弹性极限 σHEL和层裂强度 σsp等信息。其中,4 发冲击实验中只有Shot 740 没有发生层裂,处理得到该实验条件下Ni52Ti48合金的层裂强度为 (3.05 ± 0.20) GPa,Hugoniot 弹性极限 σHEL约为3.0 GPa,Hugoniot 弹性极限与Zhang 等[9]的弹塑性转变结果一致。 图12 (a)~(c) up = 0.8 km/s 时新晶粒的微结构演变,(d)~(f) 微结构演变沿x 轴的OM 分析结果,(g)~(h) 变形前后B2-NiTi 在(011)面上的投影[20]Fig. 12 (a)–(c) Microstructural evolution of new grain for shock loading velocity up = 0.8 km/s; (d)–(f) the corresponding region based on OM analysis along the x axis; projection of B2-NiTi crystal position on (011) plane before (g) and after (h) deformation[20] 层裂实验回收样品的EBSD 表征分析结果如图13 所示。当加载峰值应力 σH= 6.4 GPa 时,材料内部形成大量再结晶组织,并出现大量新晶粒,在个别晶粒内仍然可以看到孪晶组织,并且变形组织内部出现孔洞。如图13(d)所示,当加载峰值应力 σH= 8.5 GPa 时,层裂区晶粒完全被拉长和破碎,形成大量的微小晶粒,晶粒取向变化较大,且孪晶特征出现概率减小。如图13(g)所示,当加载峰值应力 σH=12.4 GPa 时,层裂区晶粒碎化严重,形成大量的微小晶粒,晶粒取向变化较大,反映材料在层裂区域具有很大的塑性变形和再结晶趋势。总之,随着加载峰值应力的增大,层裂区域的孪晶特征逐渐减弱,再结晶趋势增强。 图13 冲击拉伸实验回收样品的EBSD 表征分析结果:(a)~(c) Shot 741, (d)~(f) Shot 739, (g)~(h) Shot 738Fig. 13 EBSD characterization analysis results of samples recovered from shock tensile experiments:(a)–(c) Shot 741, (d)–(f) Shot 739, (g)–(h) Shot 738 图14 NiTi 合金冲击拉伸实验回收样品的极射赤面(赤道面)投影图:(a) Shot 741,σ H = 6.4 GPa;(b) Shot 738,σ H = 12.4 GPaFig. 14 Pole figures (equatorial plane) of the NiTi alloy recovered from shock tensile experiments:(a) Shot 741, σ H = 6.4 GPa; (b) Shot 738, σ H = 12.4 GPa 图14 显示了加载峰值应力为6.4 和12.4 GPa 时回收样品的{001}、{011}和{111}极图。可以看出,两者的极图颜色都比较明显,密度强度相差较大,其中蓝色低密度强度面积占比较大,并且都在{001}极图中存在最高密度强度,最高密度强度为24.48 和17.36。与图7 中初始NiTi 合金样品、冲击压缩加载后回收样品和准等熵加载后回收样品的极图对比表明,冲击拉伸加载后回收样品所选区域中晶向的规律性比初始样品和冲击压缩加载回收样品高,晶向织构更明显,有极强的择优取向。随着冲击拉伸加载峰值压力的增大,最高密度强度的降低也源于孪晶特征变弱、再结晶特征增强。 图15 显示了对应于图13 中EBSD 表征结果的局部变形程度以及变形结构、再结晶结构、亚结构分布。当加载峰值应力 σH= 8.5 GPa 时,层裂位置的变形局域化趋势明显,层裂发生过程中,随着加载的进行,材料内部在大变形过程中同时发生再结晶(与压缩条件类似),并且在位错密度较高位置形成亚结构(亚晶粒)。当 σH= 12.4 GPa 时,层裂位置的变形局域化趋于平均,与此同时,在层裂发生过程中,变形区域、再结晶区域和亚结构区域的分布趋于均匀。 图15 对应于图13 中EBSD 表征结果的局部变形程度以及变形结构、再结晶结构和亚结构分布:(a)~(b) Shot 739,σ H = 8.5 GPa;(c)~(d) Shot 738,σ H = 12.4 GPaFig. 15 Local deformation degree and distribution of the deformed structure, recrystallized structure, and substructure ofthe EBSD characterization in Fig.13: (a)–(b) Shot 739, σ H = 8.5 GPa; (c)–(d) Shot 738, σ H = 12.4 GPa 对不同初始环境温度(300、500 和1000 K)下三维多晶Ni52Ti48合金模型在不同冲击粒子速度(0.2、0.4、0.6 km/s)下的响应进行了MD 模拟。对MD 模拟结果沿冲击加载方向(x轴)进行切片分析,将模型沿加载方向按照每个bin 的宽度为5 Å进行划分,计算每个切片的温度T、Hugoniot 应力σxx、粒子速度等。每0.5 ps 进行一次切片分析。提取模型中最靠近自由面的bin 的粒子速度作为模拟的自由面速度[23]。不同初始环境温度和不同冲击速度对应的典型自由面速度曲线如图16 所示。 图16 不同初始环境温度及不同冲击速度下的自由面速度历史Fig. 16 Free surface velocity histories corresponding to different shock loading velocities and initial ambient temperatures 通过沿冲击加载方向进行切片分析,得到了每个bin 在各个瞬时的Hugoniot 应力,定义层裂发生前一刻的最大Hugoniot 应力为层裂强度。参考实验中根据自由面速度历史确定层裂强度的方法(称为声学方法[32]),也可以在模拟中得到对应的层裂强度。不同初始环境温度下通过沿冲击加载方向的切片分析方法和声学方法得到了层裂强度和拉伸应变率,如表2 所示。 表2 不同初始环境温度下的层裂强度和拉伸应变率Table 2 Spall strength and tensile strain rate at different initial ambient temperatures 从图17 可以看出:随着卸载拉伸应变率的增加,NiTi 合金的层裂强度增加;在105s−1的拉伸应变率下,通过实验得到的层裂强度为(3.05 ± 0.20) GPa,而在300 K 的环境温度、1010s−1的拉伸应变率下,通过MD 模拟得到的层裂强度为(10.0 ± 0.5) GPa,表现出明显的卸载拉伸应变率效应。 图17 不同应变率下NiTi 合金的层裂强度Fig. 17 Spall strength of NiTi alloys at different strain rates 基于大电流脉冲功率电磁驱动装置CQ-4,开展了近等原子比Ni52Ti48合金的平板冲击压缩和压缩加-卸载拉伸实验,借助动量陷阱和软回收实验技术,研究了冲击加载下Ni52Ti48合金的动力学响应,回收样品的显微表征结果表明:Ni52Ti48在冲击压缩过程中以塑性变形为主,包括位错、孪晶及再结晶等,而在卸载拉伸过程中变形孪晶的几率较小,变形方式主要为位错滑移和再结晶。MD 微观模拟重现了实验中观察到的奥氏体孪晶和再结晶现象,给出了{112}奥氏体孪晶的成核、扩展、位错的竞争机制以及再结晶物理机制,得到了高应变率下层裂强度随初始温度和冲击速度变化的关系。 本文介绍的Ni52Ti48合金在高压高应变率下的微观特性仅仅涉及NiTi 高压研究中的一部分,高压下NiTi 合金仍存在很多问题亟待解决。一方面,NiTi 的高压研究需要更多精妙的实验设计;另一方面,NiTi 的MD 模拟受计算规模的限制只能重现有限压力范围的实验现象,未来的研究将集中在改进势函数以及进一步扩大模拟系统的规模上,进而得到更高压力、更复杂极端条件下的NiTi 合金性能,如考虑初始缺陷的影响、辐射模拟等。此外,NiTi 形状记忆合金在微纳尺度的应用也愈加广泛,如微执行器、微泵等,其结构设计理论在微纳NiTi 研究中也将持续发挥重要作用。 感谢中国工程物理研究院流体物理研究所吴刚、陈学秒、税荣杰、胥超、邓顺益等在实验过程中给予的帮助!感谢中国矿业大学现代分析与计算中心提供的超算机时!

2 冲击压缩加载下Ni52Ti48 合金的微观特性
2.1 回收样品显微分析



2.2 孪晶、新晶粒等微结构演化的分子动力学模拟


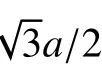


3 冲击加-卸载拉伸作用下Ni52Ti48 合金的响应特性

3.1 回收样品显微分析


3.2 多晶NiTi 层裂的MD 模拟

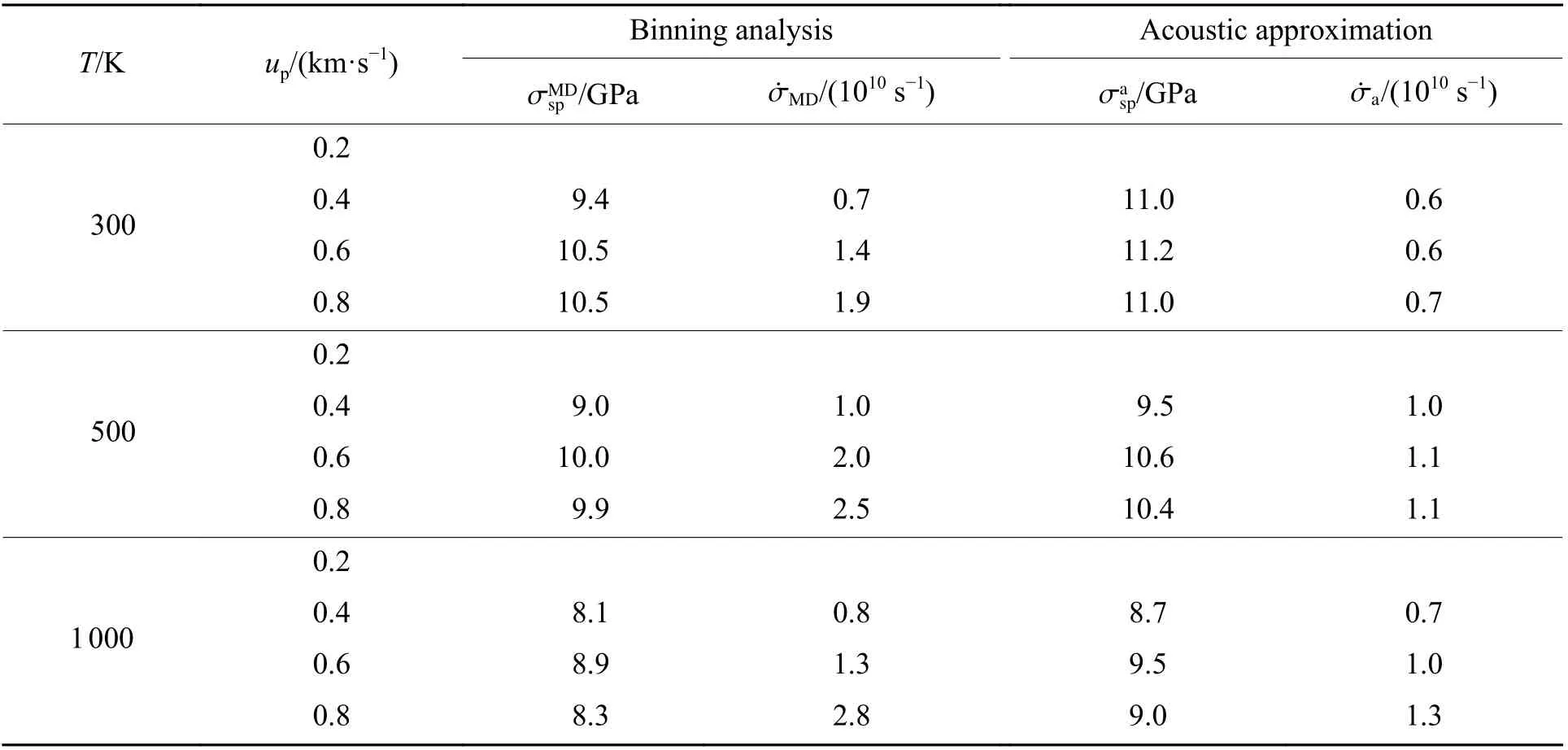
4 总 结
