马氏体相变的相场模型研究进展

于继东，姚松林，吴 强

（中国工程物理研究院流体物理研究所，四川 绵阳 621999）

相场（Phase field）模型是目前模拟材料微结构演化的重要理论与计算工具[1–5]。其优势主要体现在以下两点：（1）避免了三维空间中显示追踪界面在数学处理上的困难，相场模型通过场变量的连续变化将尖锐界面扩散为具有一定厚度的界面，界面的演化通过场变量的连续变化来实现，无需显示追踪界面，因此在处理复杂微结构演化问题上具有独特的优势；（2）相场模型基于能量泛函的表述形式，其物理模型具有良好的扩展性，可统一地在能量函数中引入力、热、电、磁等多场物理机制。目前，相场模型已广泛应用于计算材料学、计算固体力学等诸多领域，如凝固[6]、马氏体相变[7–9]、铁电铁磁相变[10]、孪晶变形[11–12]、位错动力学[13–14]、裂纹萌生与扩展[15–19]等。本文将侧重于介绍相场模型应用于马氏体相变中的相关进展。

马氏体相变是一种以切变为主的无扩散型、固固、一阶位移型相变，相转变过程极快（新相长大速度接近声速），并伴随着丰富的微结构生成，这些微结构演化与其宏观物理力学性能紧密相关，因此针对马氏体相变微结构的形成与演化开展了大量的研究工作。Ball 等[20–21]、Kohn 等[22]、Bhattacharya[23]发展了零应力平衡态下微结构形成的理论描述，对于理解微结构模式的形成具有重要的指导意义。然而，这些理论无法回答马氏体相变的动力学问题。相变动力学关注相变的转变机制和转变速率，以及其他因素（如应力、温度等）产生的影响[24]。马氏体相变过程中微结构演化与弹性应变场的相互作用非常复杂，数值模拟是研究此类问题的主要方法[7]。相关研究主要集中在不同压力、温度等外在条件下不同材料的马氏体相变的微结构演化模式，以揭示物理机制，并指导材料设计[25–31]。

本文首先概述相场模型的基本概念以及马氏体相变相场模型的理论框架，围绕相场模型的两个独特优势，介绍近年来马氏体相变相场模型的主要进展：一是基于相变路径理论建立相场模型，该模型对于加卸载条件下重构型马氏体相变的复杂微结构演化问题具有特别的适用性；二是基于相场模型在处理多物理过程中的良好扩展性，介绍马氏体相变与塑性变形耦合的相场模型的系列进展。

1 相场模型

相场模型是为研究非均匀系统的微结构演化问题而发展起来的唯象理论模型，其基本思想可追溯至19 世纪末van der Waals 提出的扩散边界的思想[32]，Gibbs[33]和Cahn 等[34]的经典工作奠定了相场模型的基础物理概念。类似于Landau 在处理连续相变问题时引入序参量的概念，相场模型引入了一系列序参量来描述非均匀系统中不同的相，系统能量不仅是序参量的函数，也是序参量空间梯度的函数，序参量的空间梯度描述的是不同相之间的界面。序参量可以有明确的物理意义，如金属合金相变问题中的质量分数、铁电及铁磁问题中的电偶极矩和磁矩，其热力学和动力学参数均有明确的物理量相对应；场变量也可以没有明确的物理意义，例如研究凝固问题中的固液界面时，场变量的引入是为了避免显示界面追踪，在这类问题中定义具有严格物理意义且数学上易于处理的序参量仍是一个挑战。守恒型序参量（如浓度）和非守恒型序参量（如马氏体变体取向）的控制方程分别为Cahn-Hilliard 方程[34]和Allen-Cahn 方程[35]。随着计算机能力的提升，从20 世纪90 年代开始，相场模型逐渐应用于凝固问题的模拟，并在涉及微结构演化一类的问题中得到广泛应用，相关研究进展可见综述[1–5]。

式中：f为局域自由能密度， αi和 βij为与界面厚度相关的梯度项系数。界面处的序参量梯度不为零，式(1)积分项中的梯度项与界面能相关。不同相场模型的主要区别体现在如何构建式(1)所示的系统自由能。例如：相的失稳分解和凝固问题中构建双势阱形式的能量函数[36–37]，位错动力学问题中构建周期性势阱能量函数[38]，马氏体相变问题中构建满足晶格对称性操作的能量函数[39]。

守恒型场变量的演化方程为Cahn-Hilliard 方程

非守恒型场变量的演化方程为Allen-Cahn 方程

式中：Mi j和Lpq为动力学系数，与原子或界面的迁移率相关，Mij和Lpq满足Onsager 关系，即Mij=Mji，Lpq=Lqp。Cahn-Hilliard 方程通过ci的守恒方程推导得到，体现了守恒型场变量的守恒性质。Allen-Cahn 方程是个唯象方程，其物理意义是场变量的演化朝着系统自由能减小的方向进行。

物质界面具有一定的宽度，如相界面厚度的典型尺度为纳米量级，当相场模型的扩散界面宽度与界面的物理尺寸相当时，相场模型的界面具有明确的物理意义，相关参数也可通过第一性原理计算获得[40–41]（如层错能等），对缺陷等微结构的演化具有预测性[5,8,42]，此类相场模型被称为微观相场模型（Microscopic phase field）[5]。在相场模型的数值模拟中，界面至少需要3～4 个计算网格，因此微观相场模型适用的空间尺度为微观尺度。目前，相场模型也广泛应用于介观尺度上的相变、位错结构、枝晶生长等问题中，此时扩散界面的宽度远大于物理界面的宽度（一般为1 个数量级），相场模型并不具备预测缺陷基本特性的能力，但在描述微结构演化过程中的复杂几何结构变化及微结构模式形成等问题时，仍能给出与实验结果一致的有价值的认识，此类相场模型称为粗粒化相场模型（Coarse grained phase field）[5]。理论上，粗粒化相场模型仅在尖锐界面极限（即通过尖锐界面的渐进分析对模型参数及控制方程进行修正）下才能给出定量化结果。Karma 等[43–44]将尖锐界面渐进分析方法应用于枝晶生长问题，将计算网格由纳米量级提升至0.1 μm量级仍可保证模拟结果的定量程度，极大地拓展了枝晶生长问题的相场模拟能力。最近，Finel 等[45]提出了一种新的方法，以提高粗粒化相场模型的界面动力学模拟精度，通过在离散形式的能量方程中引入晶格的平移及旋转不变性，从而在能量方程中引入对称性不变的限制条件，使得在一个计算网格内高精度地捕捉界面动力学特性，相关方法对于提升固固相变相场模拟的研究尺度具有重要意义。另一方面，也可通过自适应模拟技术[46–47]提高相场模拟的计算效率。有效提升粗粒化相场模型的预测能力及计算效率将是相场模型研究中持续关注的问题之一[48–51]。

2 马氏体相变的相场模型

马氏体相变有不同的分类[52]。Bhattacharya 等[53]根据逆相变的微结构可恢复性，将马氏体相变分为弱（Weak）马氏体相变和重构型（Reconstructive）马氏体相变。弱马氏体相变指的是外载卸载时，逆相变使相变微结构消失的同时，在母相中不会或仅残留少量位错和孪晶缺陷，如图1 所示的TiNi 形状记忆合金的扫描电镜（Scanning electron microscope，SEM）图像，降温时发生高温奥氏体到低温马氏体相变，形成复杂的V 形及六角形形貌，再升温后马氏体相变微结构基本消失[54]；重构型马氏体相变指的是逆相变不会使马氏体相变微结构消失，外载卸载过程会形成一系列微结构，导致母相中形成大量的位错和孪晶缺陷，如金属铁在冲击加载条件下的相变过程，图2 所示的冲击加载金属铁回收样品的透射电镜（Transmission electron microscope，TEM）图像[55]显示，回收样品中存在大量孪晶及二次孪晶组织，而初始样品中不存在这些孪晶组织，这些特征结构是材料经历相变-逆相变后形成的不可恢复的微结构。Bhattacharya 等[53]从晶格对称群的角度分析发现，当新相的对称群是母相对称群的子群时，马氏体相变微结构是可逆的，并称此类相变为弱马氏体相变，其他类型的马氏体相变为重构型马氏体相变。采用相场模型模拟两种类型的马氏体相变时，理论模型上是有明显区别的。

图1 TiNi 合金降温-升温过程中的原位SEM 图像：(a) 290 K，(b)降温至222 K，(c)再升温至265 K，(d)再升温至290 K[54]Fig. 1 Series of in situ SEM images of TiNi alloy at (a) 290 K and (b) 222 K upon cooling, and (c) 265 K and (d) 290 K upon heating[54]

相场模型的能量函数一般基于Landau 相变理论，将自由能在相变点附近展开为序参量的多项式函数。对于马氏体相变问题，按序参量的选择方式分为两类相场模型。第一类是将序参量与总应变直接关联，能量函数为序参量的多项式函数[56–58]，或者进一步考虑能量函数在晶格对称性操作下保持不变[59–61]。此类相场模型的前提条件是晶格尺度的变形与宏观尺度的应变一致，即Cauchy-Born 假设成立，对于存在塑性变形等复杂变形的问题，此类相场模型不适用。另一类是将序参量与相变应变（也称本征应变或特征应变）关联[7,26,62–65]，相变应变为零应力条件下相变导致的应变，序参量为内变量，在能量函数构建中可考虑不同内变量之间的耦合，使相场模型更易于向多场问题等复杂情况拓展。目前马氏体相变相场模型研究中主要采用第2 类方法，下面将对其进行简要介绍。

图2 冲击加载下金属铁回收样品的TEM 图像[55]Fig. 2 TEM image showing the microstructure of shock-compressed iron[55]

马氏体相变相场模型的能量函数由化学能和弹性能两部分组成。化学能描述系统的热力学特性，不依赖于应力，可表示为[8]

例如，对于“hcp→正交相”马氏体相变，满足晶格对称性操作且展开至6 次幂的化学能表示为[66]

弹性能可表示为

Cijkl(η)

式中：弹性常数为母相弹性常数和新相弹性常数的差值函数

对于多序参量问题，两种限制条件使得能量函数的构建较为复杂：一个是需要考虑不同马氏体变体之间转变的重取向问题；另一个是能量函数需在数学形式上保证两个序参量不能同时到1，即马氏体变体不能相互重叠。一般通过引入罚函数，使2 个及以上的序参量同时到1 的能量极高，从而使能量函数满足限定条件，然而随着序参量的增加，数学形式变得非常复杂，限制了这种做法向更多序参量情况的拓展。具体做法可见Steinbach[4]和Levitas 等[63]的工作。

3 基于相变路径理论的相场模型

3.1 模型简介

第2 节介绍的相场方法已成功应用于形状记忆合金等功能材料的弱马氏体相变[5,9]，但应用于重构型马氏体相变时却遇到较大困难。图3 显示了金属铁bcc（ α相）→hcp（ ε相）重构型马氏体相变加卸载过程[70]，加载过程的 α→ε相变过程存在6 个对称性相关的ε相变体（若考虑晶格内的shuffle 变形，则存在12 个等效的ε相变体），卸载时的逆相变过程不会沿着正相变的路径返回，而是形成新的bcc 相变体，存在12 个等效的 α′相变体，这种“相变-逆相变”路径的不唯一性导致大量孪晶及二次孪晶等组织结构的出现（见图2）。采用相场模型描述金属铁在加载过程中的马氏体相变问题时，需要引入19 个序参量，并且考虑多次加卸载过程时，变体数目呈几何级数增长，若采用对每个变体引入一个序参量的做法，将导致相场模型能量函数的数学形式非常复杂，数值求解变得非常困难。

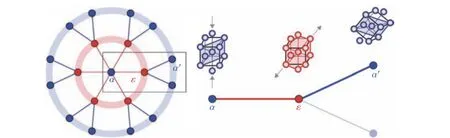
图3 铁的α→ε正相变过程（红线）及ε→α′逆相变过程（蓝线）中对称性相关的变体示意图[70]Fig. 3 Schematic illustration of the multiple symmetry-related variants for the forward α→ε (red) and the reverse ε→α′ (blue) phase transitions in iron[70]

式(12)的分解方式并不唯一，不同分解顺序的差别在文献[74]中已有分析。在小应变近似下，式(12)可退化为类似于式(8)的分解形式。将式(12)对时间求导，得到

系统的Helmholtz 自由能为弹性变形梯度、相变变形梯度和相变变形梯度的空间梯度的函数，可表述为[70]

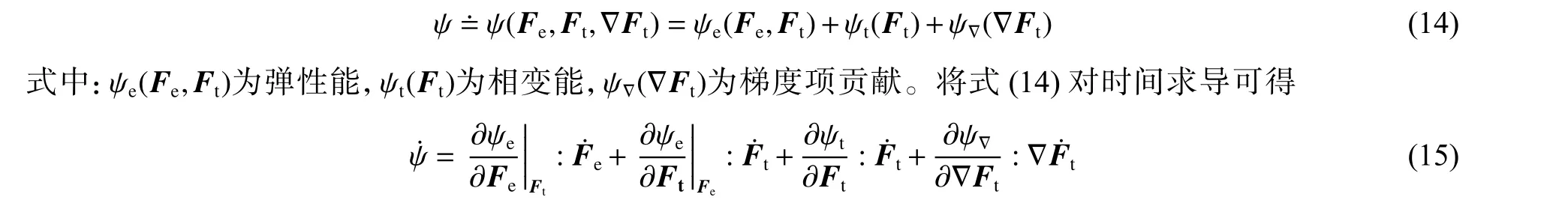
系统的耗散能大于或等于零，即Clausius-Duhem 不等式

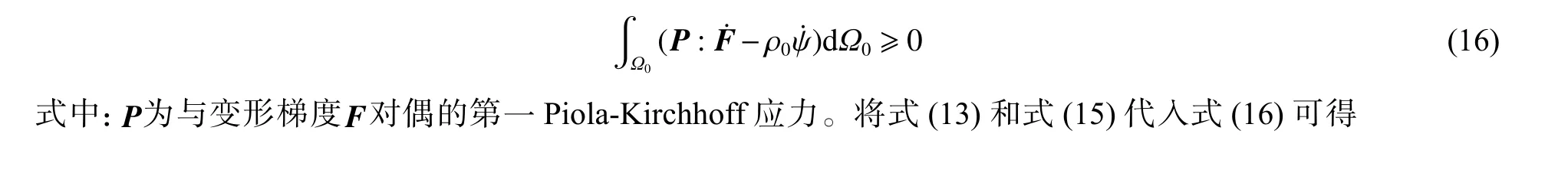
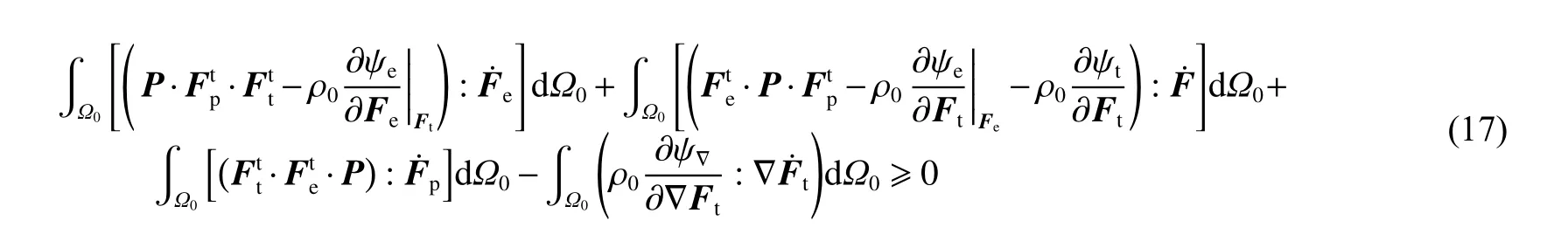
式中：第1 个积分项为弹性能（不包括黏弹性），不发生耗散，由超弹性本构描述；第3 个积分项为塑性耗散能，可由塑性屈服准则或晶体塑性模型描述；第2 个积分项和第4 个积分项为相变耗散能，借助Gauss 积分定理，可得与对偶的相变驱动力

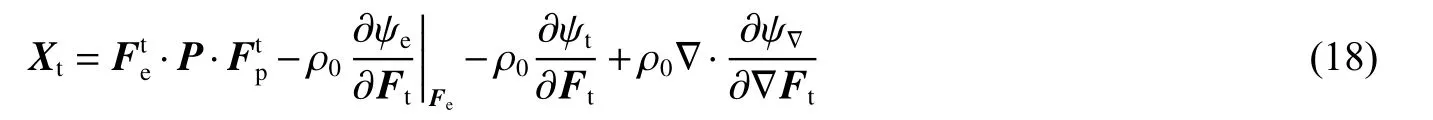
在界面各向同性的假设下，梯度项自由能表示为

式中： β类似于式(1) 中的梯度项系数。相变变形梯度的演化依赖于相变驱动力，表述为Ginzburg-Landau 方程形式[70]

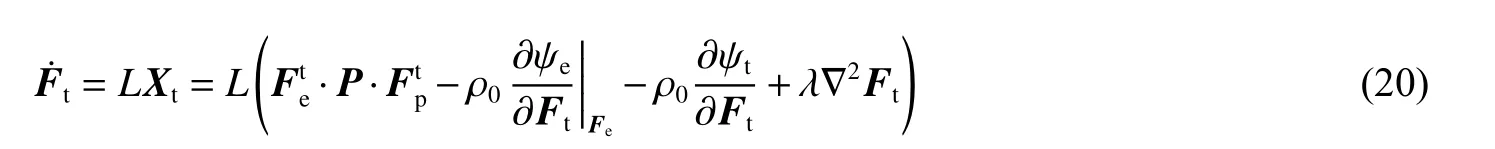
式中：L类似于式(3)中的动力学系数。与经典相场模型中每个变体对应于一个序参量的做法不同，式(20)中相变变形梯度Ft（Ft为非对称矩阵，有9 个分量）为序参量。相变变形梯度演化的关键是相变驱动力的求解，需结合超弹性本构、塑性本构及相变本构耦合求解[70]。小变形下，应力-应变关系可近似为线性关系，大变形条件下该线性关系不再满足，需采用非线性超弹性本构模型[75]。非线性超弹性本构会涉及如何确定高阶弹性模量中的相关参数，若再考虑热弹性的贡献以及弹性模量对温度和压力的依赖关系，则参数量进一步增加，不便于应用。对于高压加载情况，位错滑移、孪晶变形等塑性变形机制将剪应力水平松弛至材料的屈服强度附近，使得偏应力与静水压相比为小量，此时在本构模型中引入标量形式的状态方程，高压下仍具有较好的精度，并减少了参数量，是一种良好的近似处理。但是当加载压力与材料的屈服强度可比拟时，需采用非线性超弹性本构。

Vattré等[70,72]采用相变路径理论构建了式(20)中的相变能ψt(Ft)，其基本思路是在应变空间中基于相变本征应变及晶格对称群构建相变路径，相变遵循马氏体相变的Bain 应变机制（原子在马氏体相变过程中移动的距离最小），每个相变变体对应于相变路径中能量稳定的节点，以相变路径为基础进一步构建相变能函数 ψt，使相变沿着最接近本征应变的方向进行时能量最低。反复加卸载过程中变体数目增加，表现为应变空间中相变路径的扩展，并不增加序参量数目，避免了经典相场模型中由于序参量数目的增加导致自由能函数构建复杂性增加的问题。

对于金属材料在爆炸与冲击等强动载条件下的马氏体相变问题，反复加卸载下的马氏体相变与塑性变形互相耦合形成大量新的变体，采用基于相变路径理论的相场模型研究此类加载条件的微结构演化问题将具有良好的适用性。

3.2 相变路径理论研究

相变路径描述了马氏体相变对称性相关的变体形成基本信息，相场模型的能量函数需体现相变路径机制，相变路径和相场模型能量函数的构建是马氏体相变相场模型研究中持续关注的基础问题。相变路径和能量函数的准确建立，可合理描述相变势垒、界面能及相变的弹性松弛过程，这些因素对于马氏体相变的成核至关重要[76]，而成核过程决定了后续微结构演化的基本模式。

马氏体相变不仅有马氏体晶胞的结构变化，还存在晶胞内部的挪动（Shuffling），相场模型需构建包含这些变形自由度的能量曲面。例如：近似情况下考虑6 维的应变空间，加上3 个Shuffle 自由度，则能量函数描述的是这9 维空间中的能量曲面，相变路径可近似为连接该能量曲面中代表不同亚稳相极值点的一维曲线，曲线路径一般不是9 维空间中的直线，而是曲线甚至纠缠[77]。第一性原理计算可为相变路径的确定及能量函数的构建提供有价值的信息[78–80]。

Gao 等[81]采用群论描述晶胞的结构变化及晶胞内的原子挪动导致的晶格对称性的变化，进而定义了变形变体的概念，用于预测结构相变的相变路径。该理论已应用于不同结构相变的相变路径描述[82–83]及孪晶变形[84–85]，在相场模型的理论建模中具有较好的应用前景。

4 马氏体相变与塑性变形耦合的相场模型研究

相变和塑性变形的相互作用是材料变形研究中的基础问题[86]。马氏体相变早期共格结构的相界面存在较大的应变能，会通过塑性变形过程进行应力松弛[87]；另一方面，相变与塑性变形都是能量耗散机制，两个物理过程相互影响、相互竞争，塑性变形会改变相变序列[88]、诱导新的相变变体[70]、降低相变压力[89]等，使微结构形成模式发生改变。相场模型基于能量的表述形式具有良好的扩展性，建模中易于考虑塑性变形机制，包括孪晶变形[12]、位错滑移[13]、剪切带[90]等塑性变形机制。相变与塑性的耦合是近年来马氏体相变相场模拟研究中的热点[50,87,90–96]。

塑性变形机制通过在应变中考虑塑性应变引入。在大变形情况下，采用式(12)的变形梯度分解考虑塑性变形。在小变形近似下，式(12)可近似为

相变与塑性的耦合主要关注塑性变形对相变成核、变体结构演化等的影响。例如：Levitas 等[50]建立了一种尺度无关的、耦合位错带与马氏体相变的相场模型[50]。图4 为双晶结构在压剪条件下马氏体相变序参量分布的模拟结果，其中：图4(a)为未考虑塑性变形时，压剪作用下晶界处的应力集中导致高压相的成核及变体生长；图4(b)则考虑了两个位错滑移带，由于位错运动速度高于相变变体生长速度，因此滑移面的位错运动松弛了应力状态，改变了成核分布，另外滑移带的存在阻碍了变体的生长。

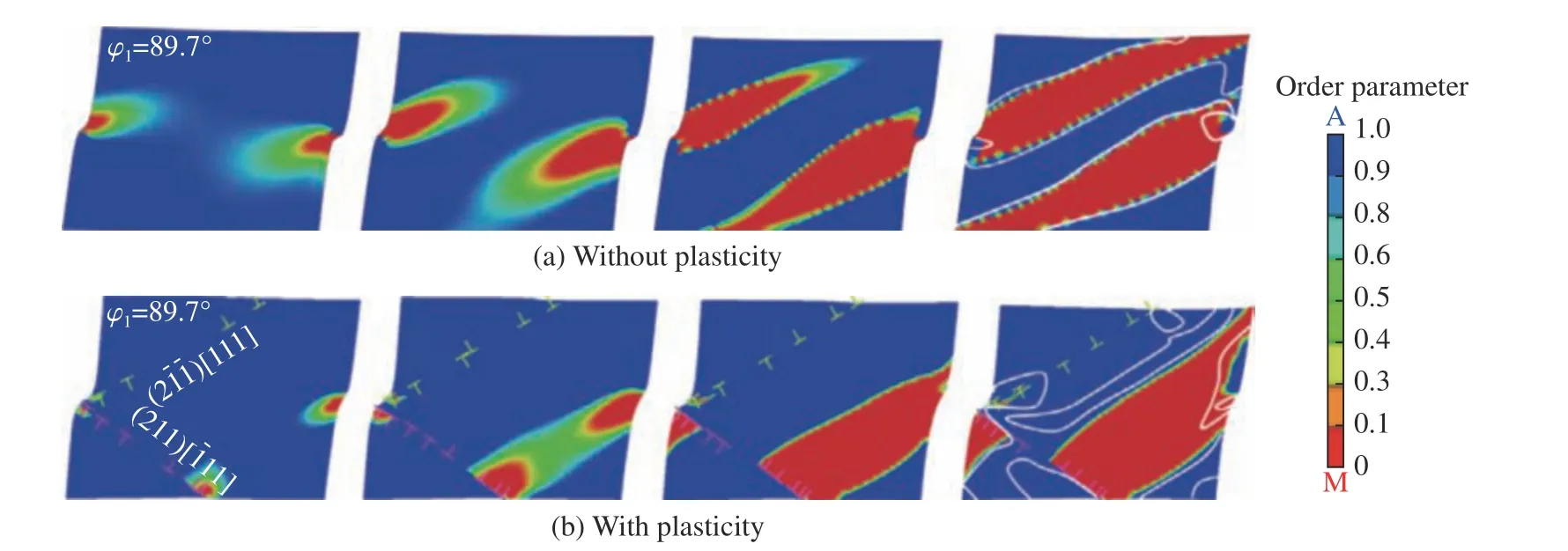
图4 塑性变形对双晶结构在压剪作用下高压相成核生长的影响[50]Fig. 4 Effect of dislocation band on nucleation and evolution of the high pressure phase of bicrystal under compression and shear[50]

5 结 束 语

相场模型是研究马氏体相变的重要理论计算方法，可揭示马氏体相变不同微结构演化模式的形成机理及影响因素，在材料科学及工程应用中发挥着积极作用。相变机制和相变路径是相场模型建立的基础，第一性原理计算可提供有价值的信息，这对提升相场模型的预测能力具有重要意义。另外，通过在能量函数中考虑塑性变形、断裂等物理过程，采用相场模型可研究马氏体相变与其他物理过程的耦合机制，相关研究是马氏体相变相场模型的重要发展方向。