高转矩密度的聚磁Halbach少极差磁齿轮设计与优化
2021-07-23戴太阳
李 辉,戴太阳,卢 敏,袁 彬,殷 毅
(重庆大学 输配电装备及系统安全与新技术国家重点实验室,重庆 400044)
0 引 言
磁齿轮相比机械齿轮具有低噪声、无摩擦、高效率、高耐久和自适应过载保护等优势,有望在未来替代机械传动机构[1-3]。然而,现阶段磁齿轮的转矩密度一般在100~290 kN·m/m3,而机械式齿轮容许转矩密度则可达到700 kN·m/m3以上,磁齿轮还面临转矩密度有待提高的问题[4-6]。
提高磁齿轮转矩密度的方法是增加磁耦合,以提高气隙磁密中的有效谐波分量,改变磁齿轮拓扑结构是增加磁极耦合的有效手段。文献[7]提出调制型磁齿轮拓扑,采用同心式结构,但需要在内外转子之间放入调制环铁心产生双层气隙结构,大大增加了内外转子之间的气隙长度,使得漏磁增加,磁极耦合程度不高,气隙磁密中有效谐波幅值难以提高,转矩密度可达100 kN·m/m3,且由于其转矩和传动比之间的约束关系,当传动比高于20∶1时,转矩密度会出现下降趋势[8]。文献[9]提出少极差磁齿轮(以下简称MGSPD)拓扑,采用偏心式结构,利用内外转子偏心产生的不均匀气隙调制磁场[10],无需使用调磁块,由此只需单层气隙结构即可实现变速传动,大大提高了气隙磁密,其表贴式MGSPD转矩密度在传动比20∶1时达180 kN·m/m3。文献[11]提出聚磁MGSPD结构,通过优化其转矩密度可达291 kN·m/m3,传动比25∶1。文献[12]将Halbach结构应用到MGSPD,转矩密度达294 kN·m/m3。但是上述结构转矩密度仍然偏低,需要探索一种转矩密度更高的磁齿轮结构。
本文将聚磁结构和Halbach结构进行组合,提出聚磁Halbach MGSPD(以下简称FFHMGSPD)结构,进一步提高了磁齿轮的转矩密度,但是其结构参数更加复杂。为深入研究各个参数对FFHMGSPD转矩的影响,通过控制变量法逐一分析新型拓扑的各结构参数与输出转矩的关系,并根据分析结果对初始设计方案进行了优化。
1 FFHMGSPD工作原理
FFHMGSPD拓扑结构,转子运动及磁钢充磁方向如图1所示。ω1表示内转子自转角速度,ω2表示内转子圆周平动角速度,ω3表示外转子自转角速度。由永磁体充磁方向可以看出,周向充磁的磁钢和铁心块构成聚磁结构,与径向充磁磁钢构成Halbach结构。该结构相比Halbach结构可以使用更少的稀土材料,相比普通聚磁结构,径向充磁的磁钢可以进一步引导磁力线的走向,提高聚磁效果。
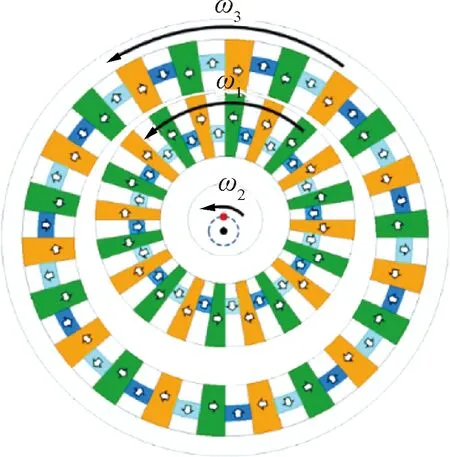
图1 FFHMGSPD拓扑
FFHMGSPD的传动结构和运行机理与机械摆线齿轮相同,在运行时,外转子固定(ω3=0),内转子既自转也进行圆周平动,两种运动方向相反,若设内转子极对数为p1,外转子极对数为p2,则传动比:
(1)
图2以一台外转子极对数p1=11、内转子极对数p2=10为例,展示了不同时刻FFHMGSPD的运动过程。当内转子圆周平动θ=360°时,内转子在外转子磁场作用下正好自转一对转子磁极角度360°/p1。

图2 FFHMGSPD运动示意图
2 模型参数计算
图3为FFHMGSPD结构参数示意图。图3中,p1、p2为内外转子极对数,β1为内转子周向充磁永磁体跨距角,β2为内转子径向充磁永磁体跨距角,α1为外转子周向充磁永磁体跨距角,α2为外转子径向充磁永磁体跨距角,h1、h8为内外转子轭部厚度,h2、h7为内外转子齿高,h3、h6为内外转子径向充磁永磁体充磁方向厚度,h4、h5为内外转子周向充磁永磁体径向高度,r0、r1为内转子周向充磁永磁体内外径,r2、r3为外转子周向充磁永磁体内外径,e为内转子的偏心量,l为轴向长度,g为最小气隙长度。以上部分参数有如下约束关系:

图3 FFHMGSPD结构参数
r1=r0+h4
(2)
r2=r3-h5
(3)
e=r2-r1-g
(4)
(5)
(6)
设计指标如表1所示,则峰值输出转矩T:

表1 FFHMGSPD设计参数
(7)
则FFHMGSPD体积:

(8)
取轴向长度l=35 mm,则可得r3=160 mm。为了布置轴承的空间足够,内转子周向永磁体内径取r0=91.5 mm。由于传动比G=25∶1,根据式(1),可取p2=26,如果选取更高的极对数,则会极大地增加磁钢装配过程复杂程度,不利于样机制造。
通过以上分析,磁钢材料和固定的结构参数如表2所示。为了方便对比转矩密度,永磁体材料采用与文献[12]中剩磁相同的永磁体NMX41SH。需要进行参数扫描的结构参数,其初始值如表3所示。由式(2)~式(4)可知,当h4,h5,r0,r3和g确定后,r1,r2和e就已确定,故表3中没有列入r1,r2和e。

表2 FFHMGSPD材料和结构参数

表3 FFHMGSPD初始扫描参数
3 结构参数优化
根据前文所得的初始设计方案,建立FFHMGSPD初始有限元模型,其结构示意图如图4所示。采用控制变量法探究表3中各个结构参数与FFHMGSPD转矩T之间的关系。
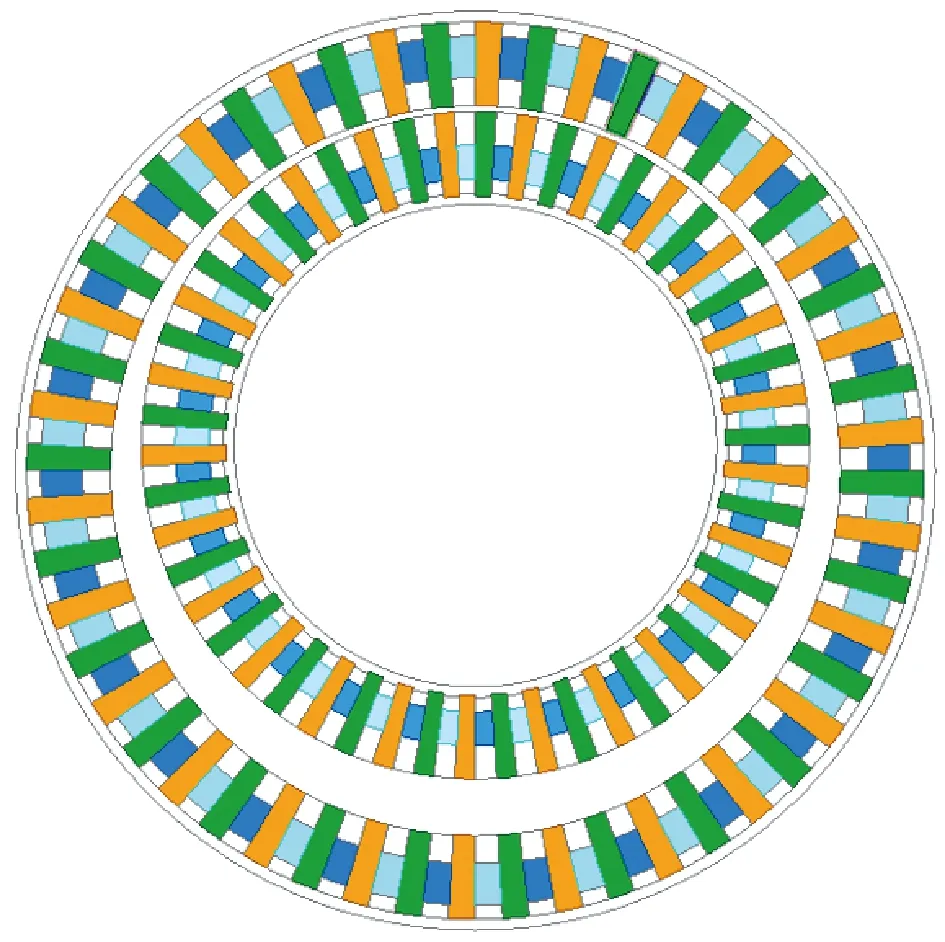
图4 FFHMGSPD初始结构示意图
3.1 最小气隙长度g与T关系
图5表示最小气隙长度g与峰值输出转矩T之间的关系。由图5可知,T是g的一次函数,且g对T的影响很大,随g增大,T将减小。但是,g不可取太小,以防止内外转子之间单边磁拉力太大,增加装配工艺难度,并对轴承使用寿命产生影响,可取g=1.5 mm。
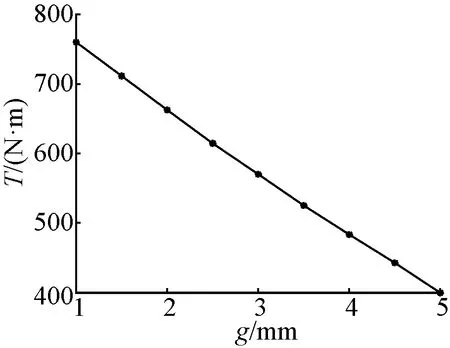
图5 g与T关系
3.2 内外转子轭部厚度h1,h8与T关系
图6表示在初始方案下,只改变内转子轭部厚度h1情况下的峰值转矩变化。由图6可知,h1对FFHMGSPD峰值转矩影响较小,且当h1=0时,T取最大值。图7表示只改变外转子轭部厚度h8时的峰值转矩变化。由图7可知,h8对峰值转矩影响也较小,且当h8=0时,T取最大值。由以上结果可知,聚磁Halbach结构,内外转子不需要增加轭部铁心,该优势将有利于减小齿轮体积,降低材料使用量,从而减小运动部件惯量,提高响应速度。

图6 h1与T关系图7 h8与T关系
3.3 内外转子周向充磁永磁体径向厚度h4,h5与T关系
由式(4)可知,内外转子齿高h2,h7和径向充磁永磁体充磁方向厚度h3,h6受内外转子周向充磁永磁体径向高度h4,h5限制,故先分析h4,h5与T的关系。图8为保持其他参数不变,单独改变内外转子周向充磁永磁体径向高度h4,h5的情况下,峰值输出转矩的变化情况。由图8可知,随着h4和h5的增加,T先快速增加,之后趋于平缓,可取拐点h4=29 mm,h5=35 mm,若继续增加永磁材料,峰值转矩增大的收益则会减小。

图8 h4,h5与T关系
3.4 内转子齿高h2和内转子径向充磁永磁体充磁方向厚度h3与转矩T关系
图9显示内转子齿高h2和内转子径向充磁永磁体充磁方向厚度h3发生变化时,峰值输出转矩的变化情况。齿高h2对T的影响较小,内转子径向充磁永磁体厚度h3对T影响较大,且随着h3增加,T增加的幅度逐渐趋于平缓,可取拐点h2=3 mm,h3=20 mm。

图9 h2和h3与T关系
3.5 外转子齿高h7和外转子径向充磁永磁体充磁方向厚度h6与转矩T关系
图10显示外转子齿高h7和外转子径向充磁永磁体充磁方向厚度h6发生变化时,峰值输出转矩的变化情况。由图10可知,外转子齿高h7对T的影响较小,外转子径向充磁永磁体厚度h6对T影响较大,且随着h6增加,T先增加后减小,可取最高点h6=15 mm,h7=0 mm。
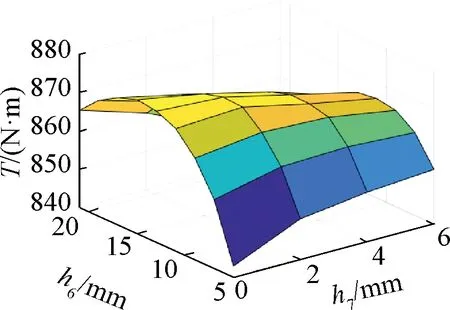
图10 h6和h7与T关系
3.6 内外转子磁钢跨距角比例i,j与转矩T关系
图11和图12显示内外转子磁钢跨距角发生变化时,静态电磁转矩随磁矩角变化曲线,也即磁矩角特性曲线簇(磁矩角即为内外磁钢产生磁场夹角的电角度,类似同步电机的功角)。由图11、图12可知,当i和j从1/1变化成其它比例时,矩角特性曲线发生移相,且峰值静态电磁转矩减小,故内外转子跨距角比例取i=1/1,j=1/1。
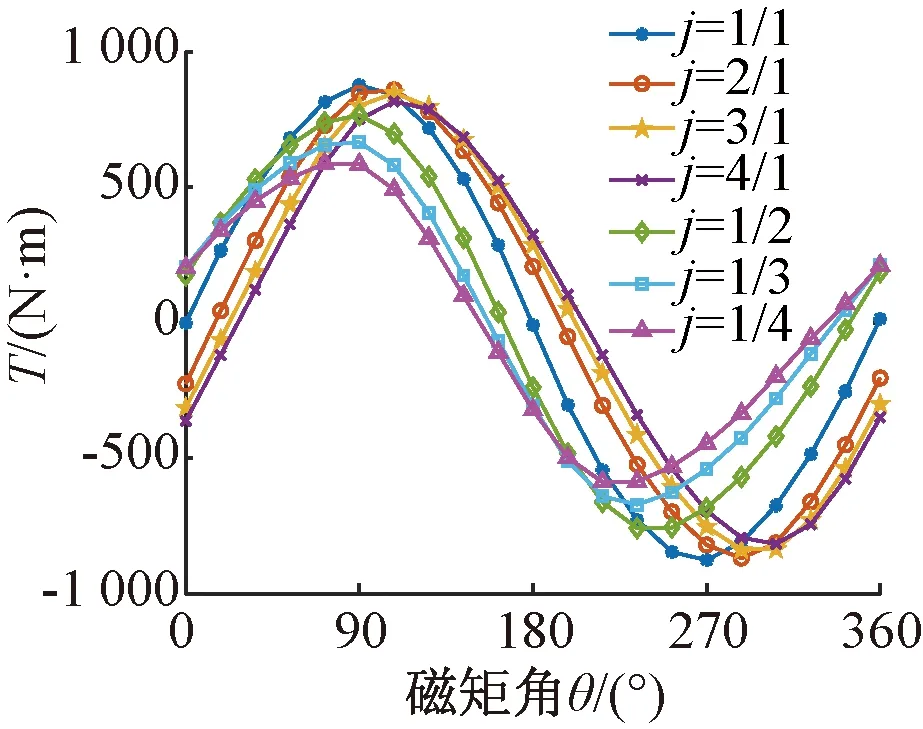
图11 j与T关系
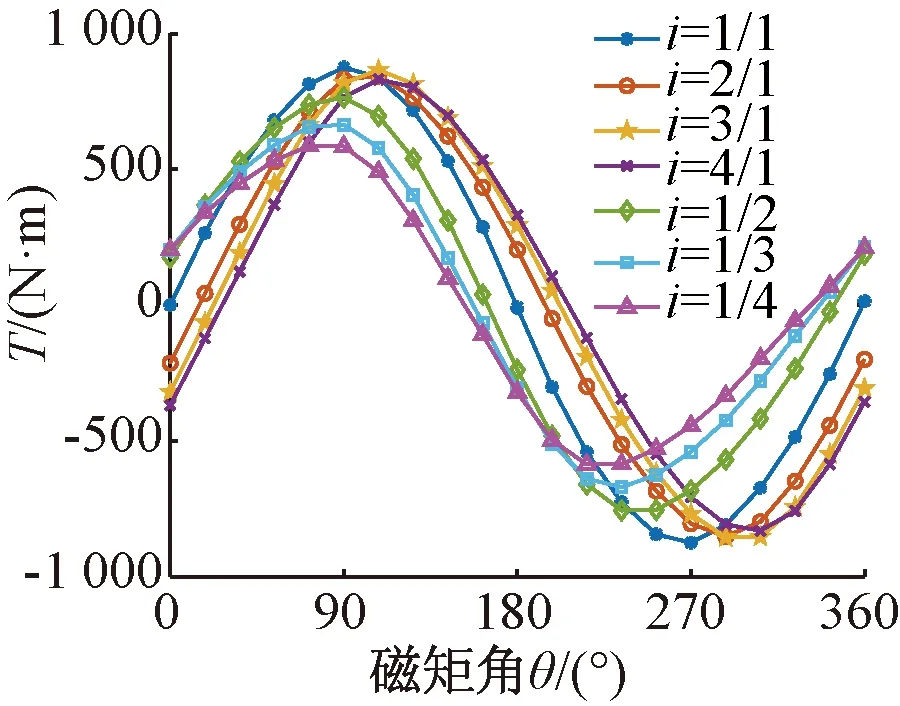
图12 i与T关系
3.7 设计方案优化
通过以上分析,最终设计方案的模型结构参数如表4所示,优化后的二维结构如图13所示。对其进行有限元计算,其剖分结果、磁密和磁力线云图如图14所示。由磁场分布云图可知,虽然该拓扑取消了磁轭,但是磁力线依然可以正常闭合,实现内外磁钢磁场之间的耦合,从而传递扭矩。其径向气隙磁密波形如图15所示,由气隙磁密分布曲线可知,气隙磁密成对称分布,对称轴即为FFHMGSPD几何对称轴,气隙磁密幅值为2.3 T。
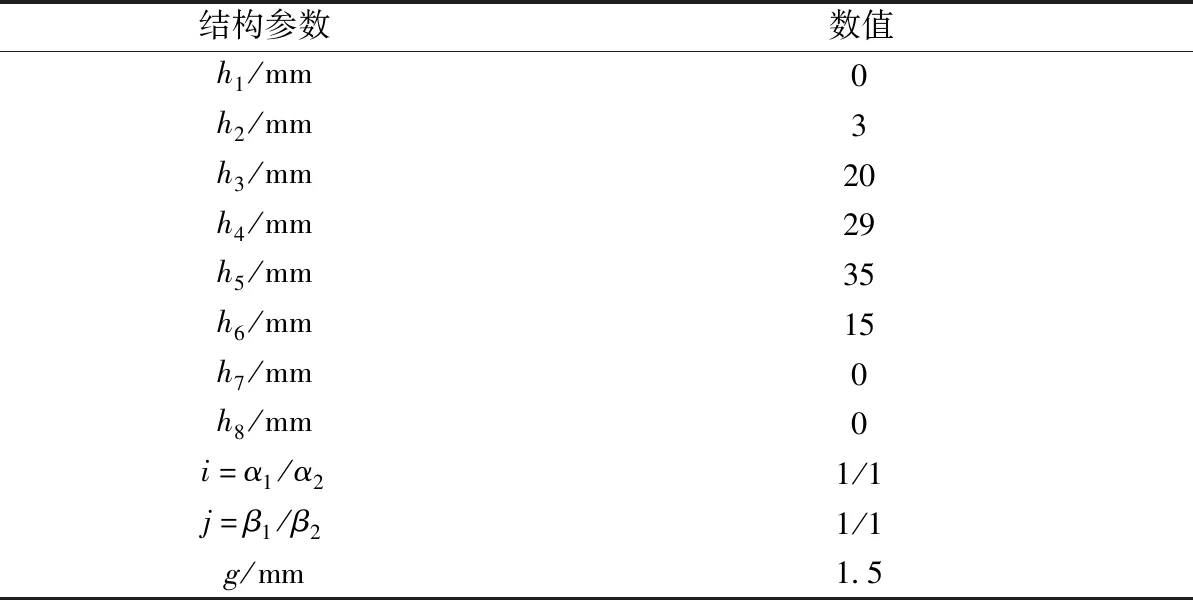
表4 FFHMGSPD最终设计方案
图13 优化设计方案结构示意图

图14 有限元剖分图和磁场云图
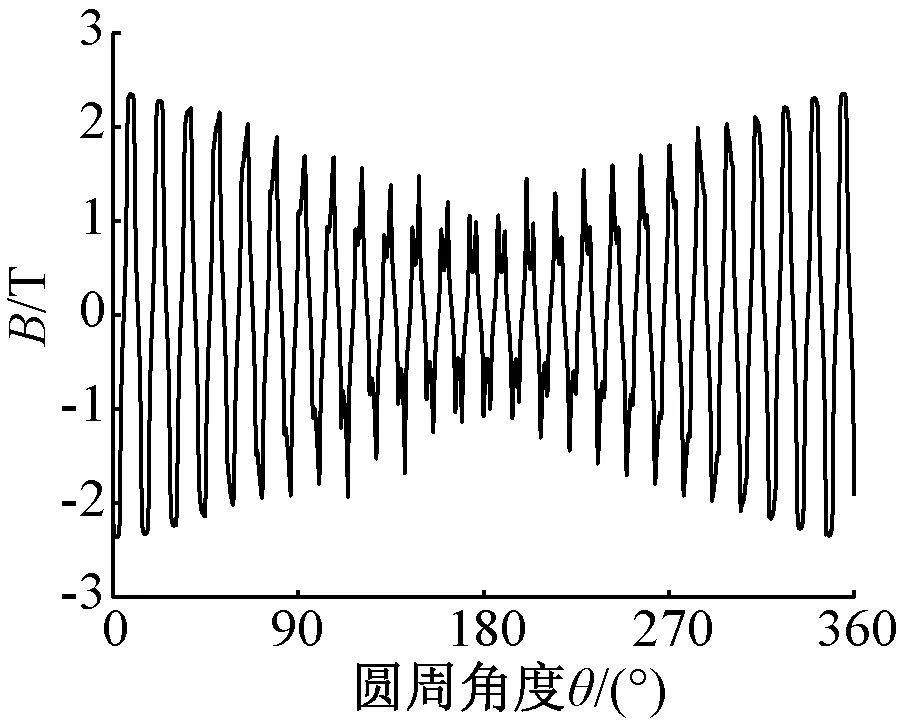
图15 气隙磁密曲线
使用有限元软件计算出磁场分布以后,使用麦克斯韦张量法即可得到内转子上所受电磁转矩[13]:
(9)
式中:μ0为空气磁导率;ne为气隙曲面s上的单位法向矢量;r为径向矢量。
图16为优化前后静态电磁转矩随磁矩角对比图,优化前模型峰值静态电磁转矩为605 N·m,优化后模型峰值静态电磁转矩可达875 N·m,提高了44%,转矩密度达310.8 kN·m/m3,相比表贴式结果的180 kN·m/m3,提高了72%。

图16 优化前后矩角特性对比
单位有效部分质量转矩由下式计算:
π(ρm-ρs)l[(r0+h2+h3)2-(r0+h2)2+
(r3-h7)2-(r3-h7-h6)2]}-1
(10)
可达75 N·m/kg,相比聚磁结构的64 N·m/kg[11],高出17%。
当FFHMGSPD以额定转速100 r/min带动恒定负载Tload=800 N·m运行时,其输出转矩稳定后如图17所示。由转矩波形可知,输出转矩脉动率仅为1.9%,磁齿轮可以平稳地带动负载运行。

图17 接恒定负载时的输出转矩曲线
4 结 语
为提高MGSPD转矩密度,本文提出聚磁Halbach少极差磁齿轮(FFHMGSPD)结构,建立了有限元模型,通过控制变量法研究了FFHMGSPD结构参数与输出转矩之间的关系,并根据分析结果对初始设计进行了优化,分析结果如下。
1)最小气隙长度g,内外转子周向充磁永磁体径向高度h4和h5,内外转子径向充磁永磁体厚度h3和h6对FFHMGSPD转矩影响较大;内外转子轭部厚度h1和h8对FFHMGSPD转矩影响较小;内外转子磁钢跨距角比例j和i会影响矩角特性相位和峰值大小,都取1/1时,峰值转矩最大。
2)优化后FFHMGSPD输出转矩达875 N·m,相比优化前提高了44%,其转矩密度可以达到310 kN·m/m3以上,单位质量转矩密度达到75 N·m/kg,相比表贴式结构提高了72%,相比聚磁结构提高了17%,转矩脉动仅为1.9%,磁齿轮可以平稳带动负载运行。
