隐极式高速永磁电机转子强度分析

2021-07-23贾金信张小波

微特电机 2021年7期

贾金信，陈彬，张小波，闫瑾

(1.空调设备及系统运行节能国家重点实验室，珠海 519070；2.广东省高速节能电机系统企业重点实验室，珠海 519070；3.珠海格力电器股份有限公司，珠海 519070)

0 引言

相比传统中、低速电机，高速永磁电机具有体积小、质量轻、功率密度大、结构紧凑、可靠性高、动态响应快以及与高速负载直连等优点，在真空泵、飞轮储能、高速电主轴、高速离心式气体压缩机等高速机器中具有广泛的应用前景[1-2]。

高速永磁电机分隐极式和凸极式两类，按磁钢形式，隐极式高速永磁电机又分实心磁钢和环形磁钢转子两类。相比采用环形磁钢的高速电机，实心磁钢类高速电机具有更高的功率密度、抗退磁能力、转子强度及转子刚度等显著优势[3-4]，应用更为广泛，尤其在超高速电机领域。

磁钢材料抗拉强度低，在高速离心力的作用下易造成磁钢失效，因此需对转子进行特殊的保护设计。目前，常用的转子护套有非金属碳纤维护套和高强度非导磁合金护套。合金护套具有工艺简单、生产一致性高等优点，因此高速转子多采用高强度非导磁合金护套。

文献[5-6]给出了环形磁钢采用碳纤维护套的解析计算表达式；文献[7]同时给出了环形磁钢采用合金保护套和碳纤维护套的解析计算公式；文献[8-9]给出了环形磁钢采用合金护套的解析计算公式；文献[10]给出了环形磁钢采用合金护套的工程简化解析计算公式。文献[11]给出了实心磁钢采用合金护套的解析计算表达式，但解析公式为偏微分解析式，工程应用受到限制，未给出简易的工程可用解析公式。

本文针对实心磁钢高速转子，进行了详细的解析推导，给出了有效的工程实用过盈量计算方法，最后通过有限元法和超速实验，验证了理论方法的正确性。

1 模型及计算原理

基于厚壁圆筒及旋转圆盘的过盈计算理论，并基于现有过盈解析计算文献[10-11]，进行高速实心磁钢转子合金护套与磁钢的简化过盈解析计算式推导。如图1所示的转子拓扑结构，磁钢内圆半径ra，保护套外圆半径rc，接触面半径rb。为方便推导，定义如下符号，如表1所示。

图1 高速转子拓扑截面图

表1 符号定义

1.1 过盈应力计算

对于过盈联接的保护套和磁钢，在接触面上产生一定的均压p，根据拉梅公式[12]，对于仅受内压p作用的护套，应力分量:

(1)

(2)

对于转子磁钢仅受外压p的作用，应力分量:

σmr1=p

(3)

σmθ1=p

(4)

1.2 考虑旋转离心力及温度因素的过盈量计算

护套和磁钢在高速离心力的作用下，位移均会发生不同程度的变化，接触面过盈量也会随着旋转发生变化。依据拉梅公式和实心轴本构方程，动态时护套的应力分量和位移分量:

(5)

(6)

(7)

同理，动态时磁钢的应力分量和位移分量:

(8)

(9)

(10)

考虑旋转因素，护套与磁钢之间过盈减少量可通过式(7)和式(10)计算：

Δδ=μsr2|r=rb-μmr2|r=rb

(11)

考虑温度因素的过盈减小修正量：

δt=(αs-αm)(Tω-T0)rb

(12)

假设结合面的装配过盈量为δ，可得护套与磁钢之间的动态过盈量：

δd=δ-Δδ-δt

(13)

(14)

综合考虑静过盈、旋转因素及温度因素，动态运行时，转子护套和磁钢的应力为两者叠加，则护套、磁钢的应力分量及护套的米塞斯等效应力：

σsr=σsr1+σsr2

(15)

σsθ=σsθ1+σsθ2

(16)

σmr=σmr1+σmr2

(17)

σmθ=σmθ1+σmθ2

(18)

(19)

对于塑性材料，米塞斯理论更接近工程实际。合金护套的最大等效应力σsvon-Mises需满足：

σsvon-Mises≤[σs]

(20)

对于脆性材料，机械应力通常采用最大拉应力理论作为判定依据。因此，永磁体的最大拉应力需满足：

σmθ≤[σm]

(21)

2 过盈量及应力解析法计算

2.1 装配过盈量计算

电机额定转速60 000 r/min，按1.2倍转速设计，即72 000 r/min。护套和磁钢的安全系数取1.2，即许用应力[σs]、[σm]分别为875 MPa和53.3 MPa。rc，rb分为15.5 mm，12.5 mm。Tω和T0分别为150 ℃和20 ℃，护套及磁钢的物性参数如表2所示。

表2 磁钢与护套物性

根据式(11)～式(14)，求得Δδ=0.011 2 mm，同时计算温度因素导致的过盈量减小量δt=0.012 7 mm。

给定初始装配过盈量δ，依据式(15)～式(21)，迭代直至满足判定条件。最终计算出满足条件的过盈范围为0.029 2 mm～0.056 7 mm。

2.2 解析法应力计算

采用解析法计算上述过盈边界条件下，护套和磁钢内的极限应力分布，如表3所示，其中负号表示压应力，正号表示拉应力。最小过盈时(δ=0.029 2 mm)，磁钢外表面压应力63.8 MPa，磁钢圆心处应力大小为35.8 MPa，此时为受压状态，护套最大等效应力443.4 MPa；最大过盈时(δ=0.056 7 mm)，磁钢外表面压应力137.2 MPa，护套最大等效应力831.6 MPa，接近护套许用应力极限。

表3 解析法计算的应力

3 有限元对比分析及样机验证

3.1 转子强度有限元对比分析

建立有限元仿真模型，忽略转轴端部效应的影响，仿真计算出转轴在轴向对称中心处沿径向的应力分布，模型如图2所示。

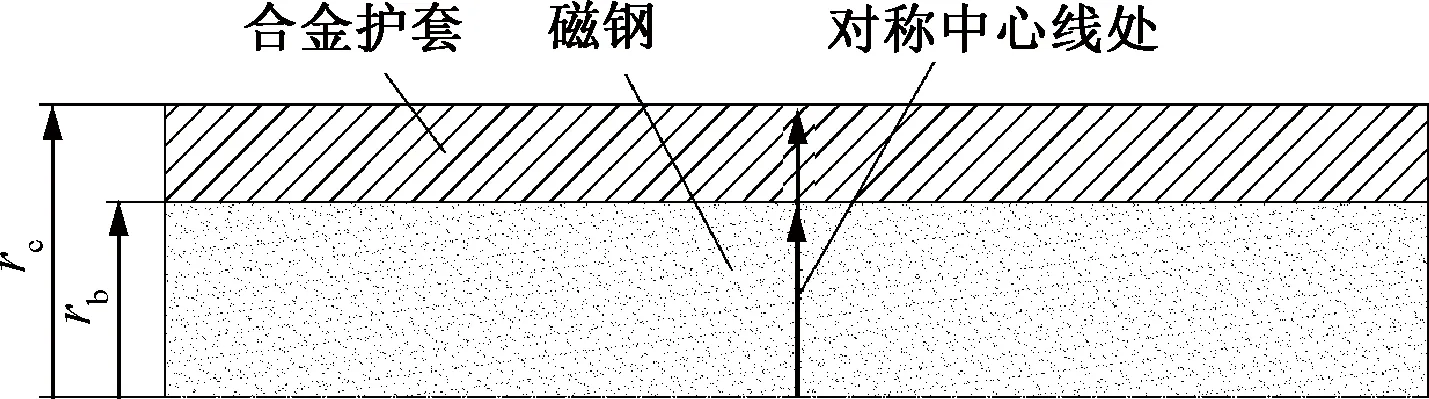
图2 转子模型截面图

本文仅选择过盈上边界进行对比分析，即在最大过盈量为0.056 7 mm，转速72 000 r/min条件下，分别采用解析法和有限元法计算的护套和磁钢的应力，详见表4。由表4可知，转子各部件应力采用解析法和有限元法计算一致性较高，磁钢各部分最大偏差仅为1.9%，护套各部分应力最大偏差为1.7%。

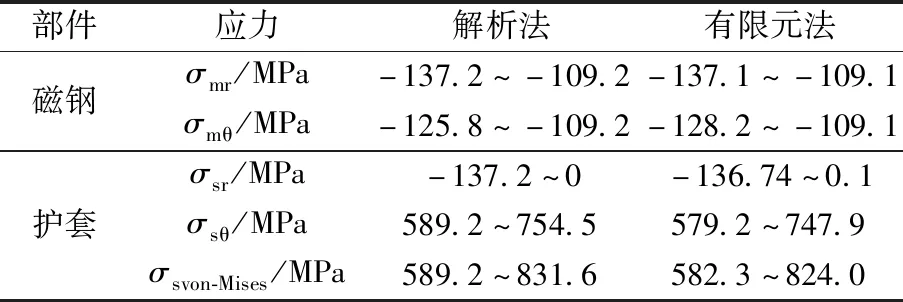
表4 解析法与有限元法计算的应力范围

磁钢径向和切向应力大小均随着磁钢半径的增加而增加，且都处于受压状态。在r=0时，即磁钢圆心处，径向和切向应力相等，随着半径的增大，切向应力大小逐渐小于径向应力。如图3所示，径向方向不同位置处，有限元法与解析法计算的磁钢径向和切向应力一致性较高，在圆心和表面处的应力偏差略微大一些，但均在2%以内。

图3 磁钢应力对比图

护套等效应力随半径的增加逐渐减小，其中径向和切向应力均随护套半径的增加而减小，径向处于受压状态，而切向处于拉应力状态。如图4所示，径向方向不同位置处，有限元法与解析法计算的护套径向和切向应力一致性较高，径向应力基本无偏差，切向和等效应力略有偏差，偏差小于2%。

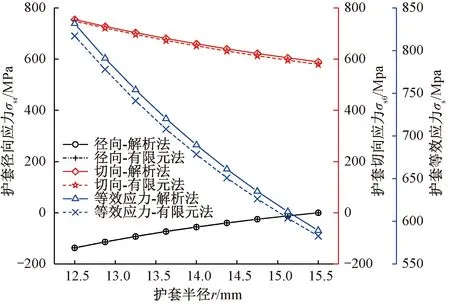
图4 护套应力对比图

在1.2倍额定转速下，仿真了转子在过盈量上、下边界时的应力分布。图5显示了磁钢的径向、切向应力分布；图6显示了护套等效应力分布。可见，相同转速下，随着过盈量的增加，磁钢表面压应力增大，心部拉应力减小，磁钢安全，而护套等效应力却急剧增大，护套容易失效。

图5 72 000 r/min时磁钢应力分布

图6 72 000 r/min时护套应力分布

3.2 样机实测验证

基于上述解析计算方法，设计了一款高速样机，高速实心磁钢转子如图7所示。转子超速实验采用自驱方式，轻载拉升至1.2倍额定转速，即72 000 r/min下，运行至少2 min，停机后，拆机分析轴系，检测转子无异常，验证了转子设计的有效性。图8分别记录了超速实验下，1.2 kHz时的轻载电流波形和停机瞬间的空载反电动势波形。