气门油封结构参数设计及优化*

雷 刚 谭 巍 樊 伟 范冬冬

(1.重庆理工大学汽车零部件先进制造技术教育部重点实验室 重庆 400054； 2.浙江吉利汽车研究院有限公司 浙江宁波 315336)

气门油封是发动机总成中的重要零部件，其密封性能对发动机的总体性能有着重要影响。随着汽车工业的发展，发动机整机性能不断提高，气门杆速度不断提升，这对气门油封的密封性能提出了更加严苛的要求。行业标准对气门油封的基本结构参数设计给出推荐值，但是油封细部参数的设计仍然依靠油封生产企业结合自身的设计经验来确定，这样将会导致相同规格、相同材料的气门油封由于不同企业细部设计的差别，在密封性能和使用寿命上表现出较大的差异。

以往对油封密封性能的研究已经形成一系列研究成果[1-6]。目前对于油封密封性能的研究主要是通过建立油封的有限元模型，或者通过台架实验进行测量。李莉英[7]对气门油封进行弹性模量测定、径向力测定和寿命实验等，并对设计参数进行总结，计算了油膜厚度，以验证气门油封唇口的最佳参数。吕迪[8]分析了影响气门油封机油泄漏量的要素，建立了有限元模型对其中一些要素进行模拟仿真，并设计台架试验进行对比验证。张付英等[9]研究了弹簧劲度系数、过盈量等对唇形油封密封性能的影响。上述的研究大多考虑的是单一结构参数对油封密封性能的影响规律，并未考虑多个油封参数共同作用下的油封密封性能。因此，针对多结构参数共同影响下油封密封性能的研究和优化，是非常有必要的。

本文作者以初始气门油封为基础，基于正交试验设计原理，对气门油封油面角、气面角、过盈量、弹簧刚度、唇口圆角半径等结构参数进行正交试验方案设计，利用有限元方法模拟分析气门油封唇口接触压力分布，进而计算得到最大接触压力和单位周长径向力2个密封性能指标；通过极差分析，确定气门油封各结构参数对油封接触压力和径向力影响的主次顺序，并以油封最大接触压力和最小单位周长径向力为目标函数优化气门油封结构参数，获得满足目标函数的最优气门油封结构参数组合。

1 气门油封几何模型

文中研究的油封模型为发动机气门油封，其几何模型如图1所示。油封总成由橡胶本体，金属骨架和压紧弹簧3部分组成。气门油封的结构参数包括油面唇角α、气面唇角β、安装过盈量δ、油封唇口圆角半径r和压紧弹簧的弹簧刚度k。气门油封初始设计参数如表1所示。

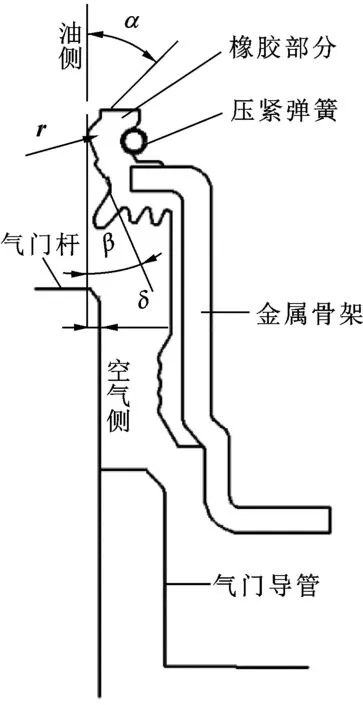
图1 油封几何模型

在气门油封设计之初，油封与气门杆之间会有一定的过盈量，油封依靠唇口的橡胶变形与气门杆形成初始的接触状态来获得密封。金属骨架的作用是用来支撑油封，保证油封有一个良好装配状态。橡胶老化会导致油封径向力衰减，而压紧弹簧可以补偿油封接触所需要的径向力，从而提高油封的使用寿命。

2 气门油封结构参数正交试验设计

依据正交试验设计原理[10]，将气门油封油面唇角α、气面唇角β、安装过盈量δ、唇口圆角半径r、弹簧刚度k5个参数定义为设计因素，气门油封参数参照GB/T 34028—2017《发动机气门导杆往复油封及性能试验方法》中推荐范围值进行确定。分析气门油封各结构参数对油封最大接触压力和单位周长径向力等接触性能参数的影响，并以最大接触压力和最小单位周长径向力为目标值，寻求油封结构参数的最优组合。正交试验设计方案因素水平参数如表2所示，其中字母A～E表示正交试验因素，数字1～4代表各试验因素水平值。根据正交试验的因素及各因素的水平值，选择5因素4水平的L16(54)正交试验表进行试验方案的排列组合，正交试验方案如表3所示。

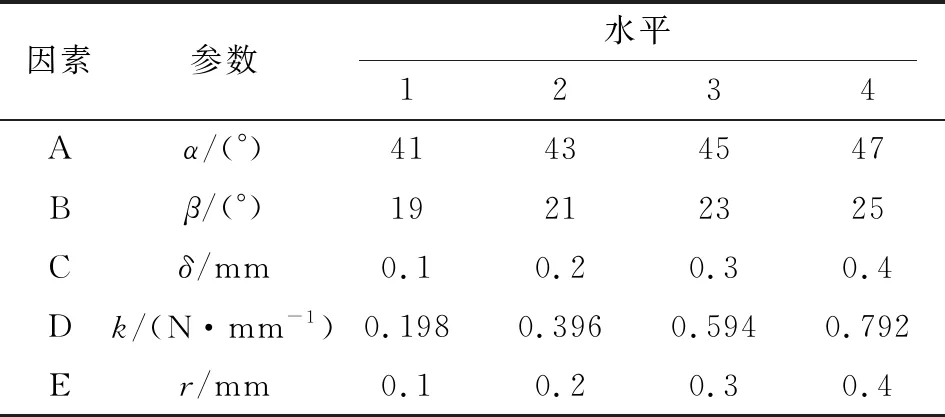
表2 正交试验因素及水平

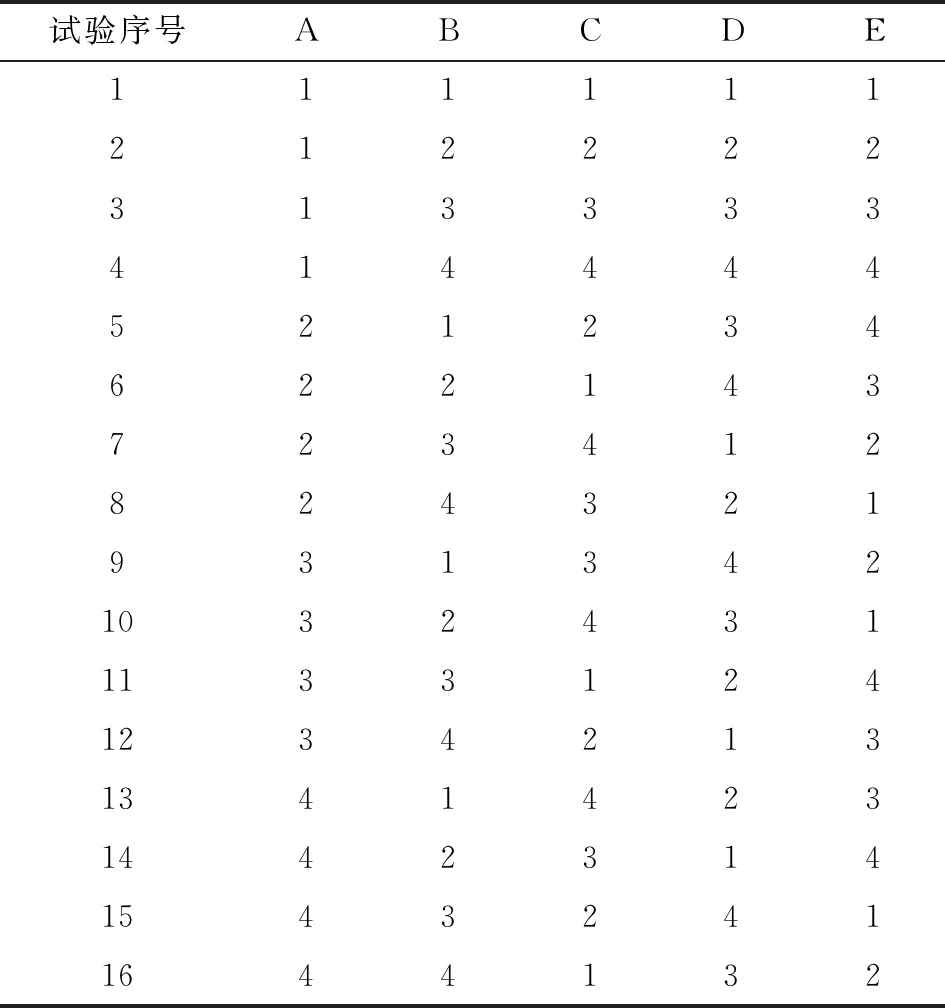
表3 L16(54)正交试验方案

3 有限元分析模型

结合表3油封各结构参数正交试验设计方案和有限元分析方法，对气门油封进行有限元模型的建立。采用有限元分析软件模拟16种方案下带簧气门油封的密封状态，计算获得各方案油封接触压力和接触宽度，进一步计算得到油封最大接触压力和单位周长径向力数值大小。

3.1 气门油封网格划分

发动机气门油封由橡胶本体、金属骨架和压紧弹簧3部分组成，在不考虑油封偏心安装时，油封结构在几何结构、约束条件和载荷施加上都表现为轴对称。因此，在油封建模时选择建立油封结构的子午面模型，对子午面模型进行网格划分，然后用有限元软件进行计算。橡胶部分、压紧弹簧、金属骨架采用四边形轴对称减缩积分单元，气门杆和气门导管按照解析刚体建立模型。经过试验，网格划分的数量和大小对仿真结果没有影响。

为了能对气门油封压紧弹簧进行模拟，在创建油封模型时对压紧弹簧结构进行相应的简化处理，以便在分析中尽可能模拟压紧弹簧的作用。简化后的弹簧模型呈圆管状，用圆管的等效弹性模量E来表征弹簧刚度k的数值。具体推导过程[11-12]如下：

F=k·ΔL

(1)

(2)

(3)

σ=E·ε

(4)

(5)

式中:F为弹簧拉力(N)；k为弹簧劲度系数(N/mm)；ΔL为弹簧拉伸变形量(mm);L为弹簧原长(mm)；ε为拉伸应变；σ为拉伸应力(N/mm2);S为圆管横截面积(mm2)。

气门油封网格划分结果如图2所示。

图2 油封网格划分结果

3.2 材料模型

橡胶属于超弹性材料，在力学性能上表现出强烈的非线性特性，橡胶材料的应力应变关系通常采用应变能密度函数来描述。橡胶应变在150%以内变形，两参数的Mooney-Rivlin 模型能够很好地描述橡胶材料的力学性能，此模型与试验数据也有很好的一致性[13]。两参数的Mooney-Rivlin 模型[14]描述如下：

U=C10(I1-3)+C01(I2-3)

(6)

式中：U为单位体积的应变能；C01、C10为材料系数;I1、I2为一阶、二阶应变不变量。

用于气门油封橡胶本体材料为氟橡胶(FKM),硬度为Shore A 72。根据FKM橡胶的硬度，经过计算得到橡胶材料系数C10=0.812 MPa，C01=0.203 MPa。气门油封内包金属骨架材料为碳钢，弹性模量为210 GPa，泊松比为0.3；气门杆和气门导管按照刚体处理。

3.3 接触设置和边界条件

气门油封系统在模拟分析过程中，需要建立气门杆和油封唇口的接触、气门导管与油封的接触、油封与弹簧的接触对才能保证力的传递。3组接触均采用面-面接触的方式，切向摩擦因数设置为0.3。

约束气门油封底部的全部自由度。在代表气门导管的解析刚体上施加沿Y方向的位移值，大小为8 mm,在代表气门杆的解析刚体上施加沿Y方向的位移值，大小为10 mm。

4 有限元分析结果

4.1 初始油封有限元分析结果

待Abaqus计算完后，截取到的应力云图如图3所示。将Abaqus中的数据导入Origin后，得到的接触应力在接触宽度上的分布如图4所示。

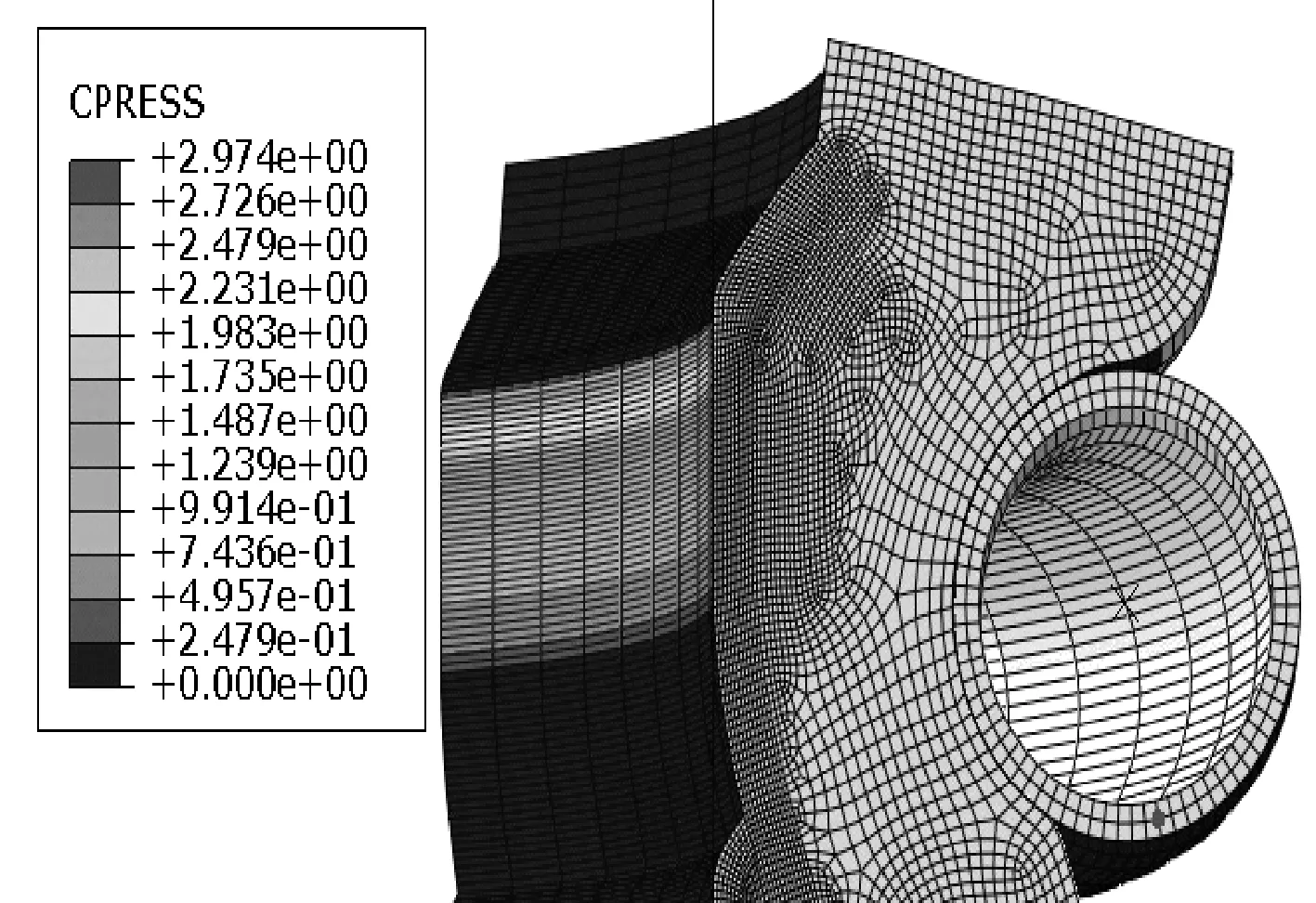
图3 初始油封接触压力云图(MPa)

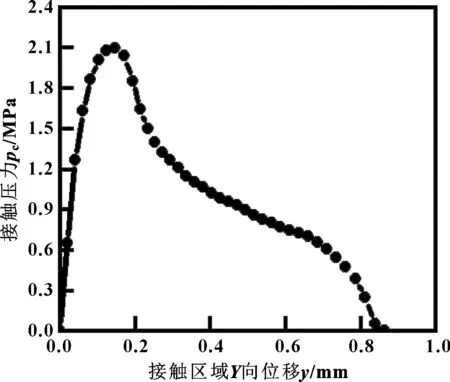
图4 接触压力沿Y轴向分布

由图3所示接触应力云图可以看出，初始油封的大部分接触区域的接触压力都在0.7 MPa以上，而最大接触压力达到了2.9 MPa左右。对于无压或低压(0.3 MPa)油封环境来说，初始油封的接触压力明显大于油压,所以能够起到良好的密封作用。由图4所示接触压力沿Y轴向分布可以看出，油封唇接触压力呈现不均匀分布，接触压力最大值位置靠近油侧。副唇的设计可以防止灰尘进入密封唇口。

4.2 正交试验方案的有限元分析结果

表4汇总了气门油封正交试验16种方案的接触宽度、最大接触压力和单位周长径向力分析结果。

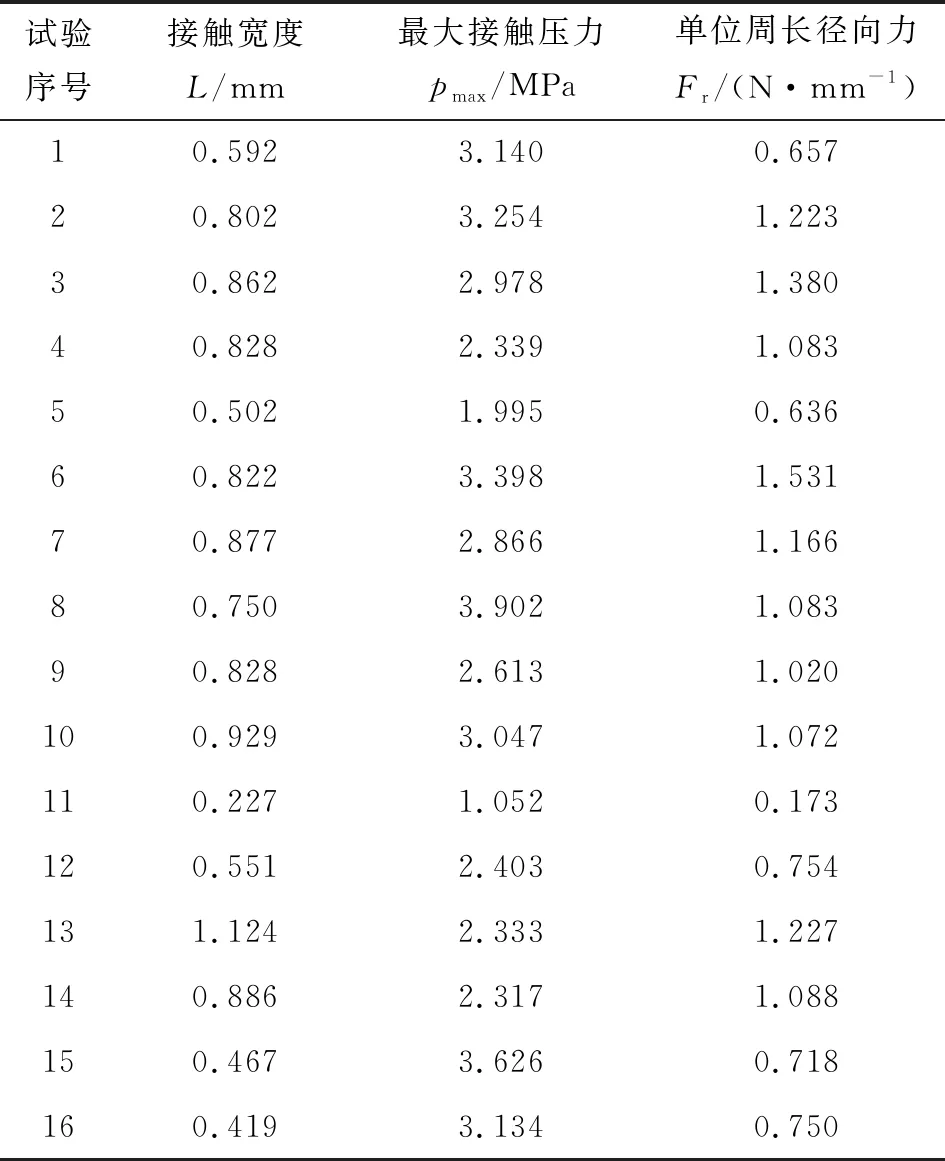
表4 正交试验分析结果

5 正交试验结果分析

为了研究气门油封结构参数对油封密封性能的影响规律，选取油封唇口最大接触压力pmax和单位周长径向力Fr2个性能指标，分析油封各结构参数对2个性能指标影响的主次顺序；并以最大接触压力和最小单位周长径向力作为优化目标，寻求油封结构参数最优组合。

5.1 试验数据极差分析

极差分析(直观分析)：通过极差的大小来评价各因素对试验指标影响的程度。极差值表示第i列因素各水平平均指标值的最大值与最小值之差,即

Ri=max{kij}-min{kij}

(7)

式中：i为正交试验因素数(A～E)；j为各因素水平数(1～4)；ki为任意列上水平号为i时所对应的试验指标和的算术平均值[15]。

为了探寻油封结构参数对油封密封性能的影响规律，研究油封诸多结构因素对油封最大接触压力pmax和单位周长径向力Fr的影响顺序，寻求最优的油封结构参数组合，需要对正交试验方案分析数据进行极差分析。经过分析计算，极差分析结果如表5所示。

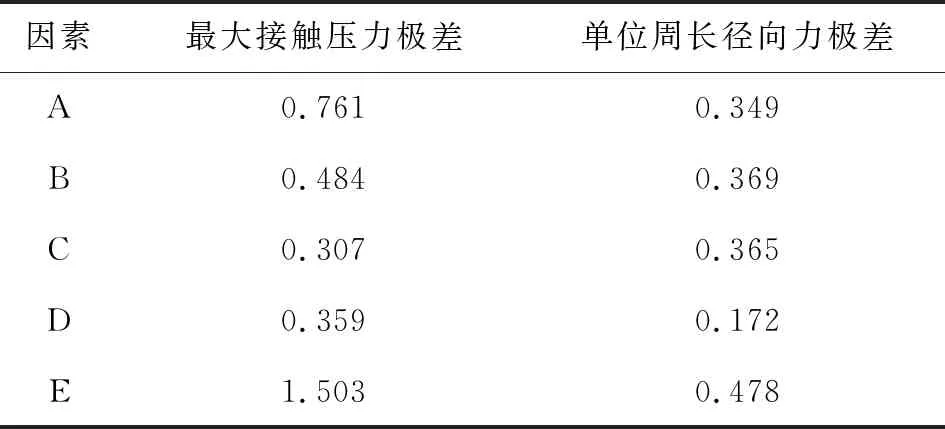
表5 各因素极差分析结果

极差值通过试验因素水平的改变，来反映目标值变化的波动情况，进而分析出各因素对目标性能的重要程度。因素的重要性与极差值的大小呈正相关，极差值越大，说明因素对目标性能的影响程度越大，通过极差的分析就可以反映出油封各结构参数对油封静态密封性能影响的主次顺序。从极差分析结果可以看出，影响气门油封最大接触压力的结构参数主次顺序依次为：E、A、B、D、C，影响单位周长径向力的结构参数主次顺序依次为：E、 B、C、A、D。由此可见，因素E(即油封唇口圆角半径)对油封唇口最大接触压力和单位周长径向力的影响程度都为最大；因素B(即气面角)对单位周长径向力有较显著的影响；因素A(即油面角)对油封唇口最大接触压力有较强的影响，但对单位周长径向力影响较小；因素D(即弹簧刚度)对单位周长径向力和最大接触压力影响均较小。

5.2 气门油封最优结构方案确定

为了探究气门油封最优结构参数组合，以最大接触压力和最小单位周长径向力为优化目标，计算出同一水平下各因素的数值均值，获取各因素最优水平组合，再结合极差分析结果，确定出满足优化目标的最优结构参数组合。最大接触压力均值和单位周长径向力均值如图5、6所示。2个优化目标的各因素最佳水平如表6所示。

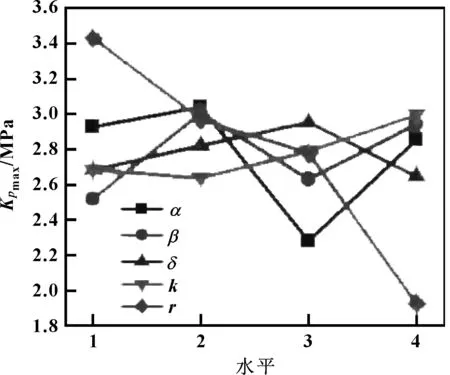
图5 最大接触压力均值

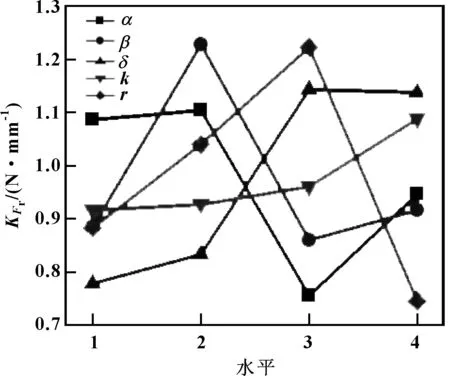
图6 单位周长径向力均值

表6 各因素最优水平数

由表6可知，每个因素对于最大平均接触压力和最小单位周长径向力2个优化目标的最优水平并不完全相同。结合图5、6极差分析结果，则可以确定出各因素对2个优化目标的最优水平组合为：油面角α=43°，气面角β=23°，过盈量δ=0.1 mm，弹簧刚度k=0.792 N/mm，唇口圆角半径r=0.1 mm。

5.3 油封最优方案的优化结果分析

由正交试验方案得到的最优油封结构参数组合对气门油封进行建模分析，计算得到优化后的气门油封最大接触压力和单位周长径向力，并与初始油封密封性能评价指标进行比较，突出优化后气门油封密封性能的提升。图7所示为油封优化后的接触压力云图，图8所示为其接触压力在接触宽度上的分布。

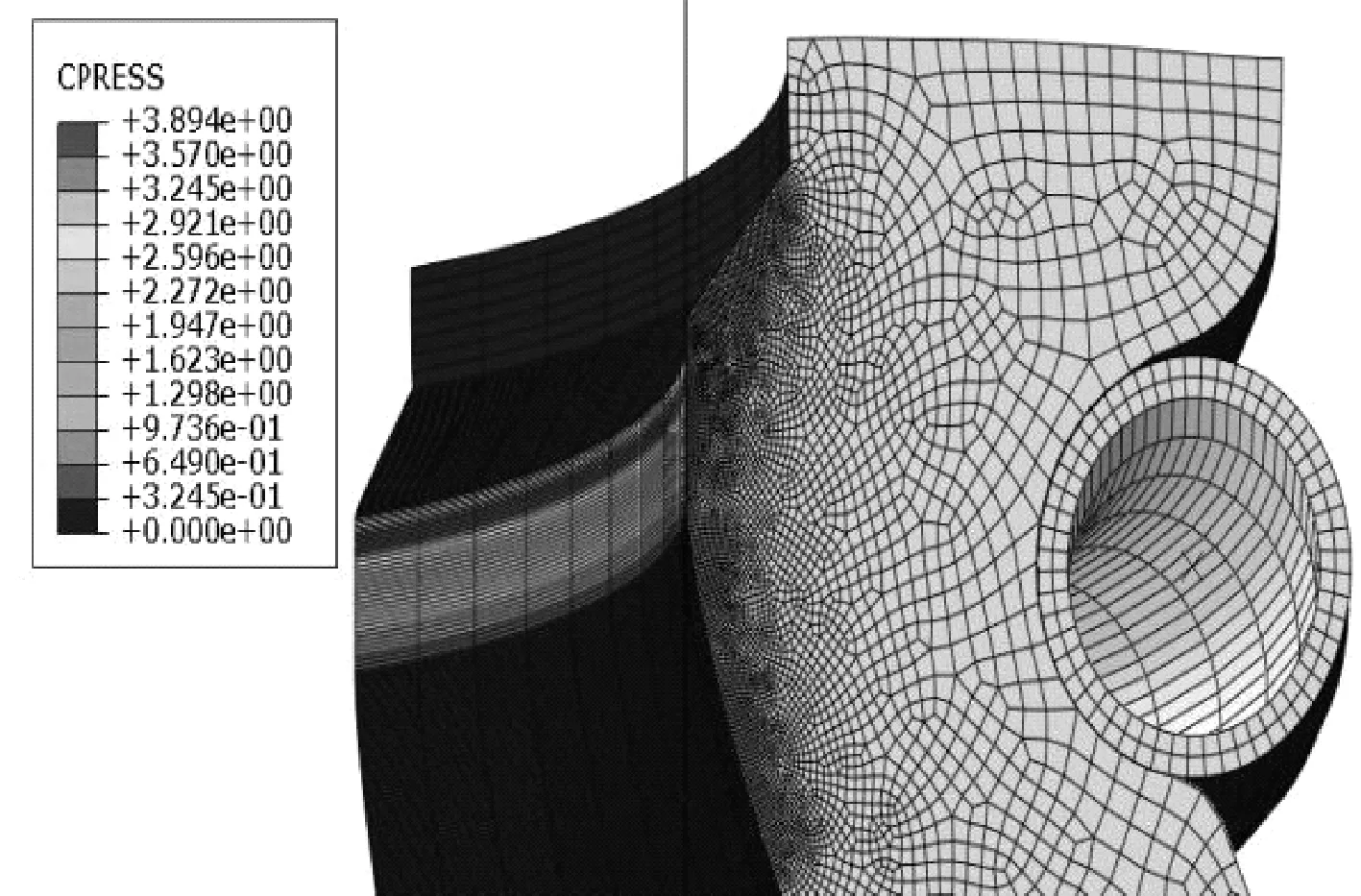
图7 优化后油封唇口接触压力云图(MPa)

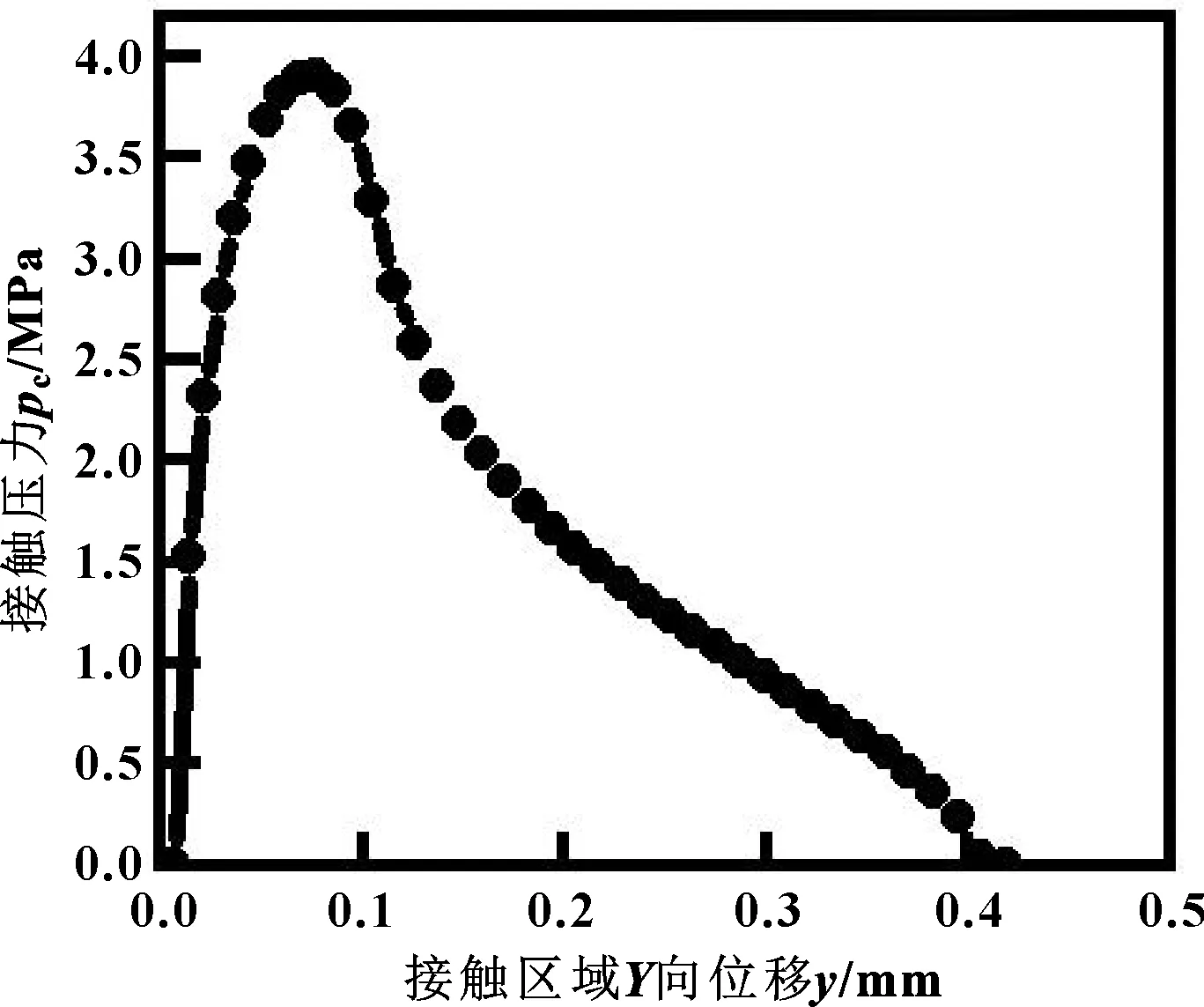
图8 优化后油封唇口接触压力沿Y轴向分布

对比图7、8和图3、4可以发现，优化后油封的唇口压力分布最大处的接触压力比初始油封要明显更大，说明优化后油封的密封性能要明显提高；同时优化后油封的接触宽度要明显短于初始油封的接触宽度，说明优化后油封的磨损情况将会减轻。具体计算结果如表7所示。

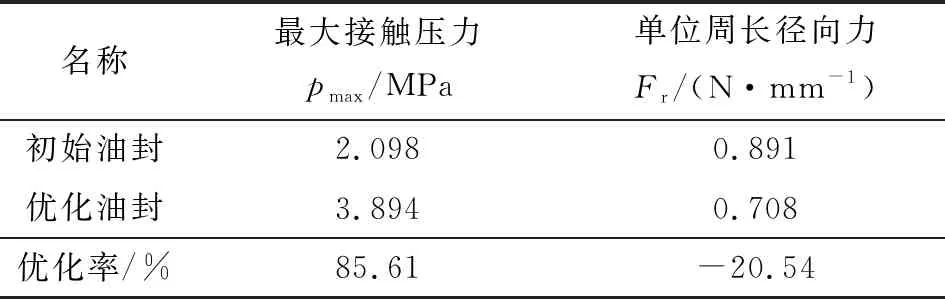
表7 初始油封与优化油封性能对比

根据表7计算结果可以看出，优化后的气门油封在最大接触压力上比初始油封增加了85.61%，对于无压油封或油压小于0.3 MPa的油封来说，最大接触压力大于油压即可保证油封的静态密封性能。油封的径向力亦称抱轴力，径向力过大，将会加剧油封唇口磨损，严重影响油封的使用。从表7可看出，优化后的油封单位周长径向力比初始油封减少了20.54%，在保证油封密封性的前提下，大大改善了油封唇口的磨损情况，提高了油封的使用寿命。

6 结论

(1)正交试验及极差分析结果表明：油封结构参数对最大接触压力影响的主次顺序依次为唇口圆角半径、油面唇角、气面唇角、弹簧刚度、安装过盈量；对单位周长径向力影响的主次顺序依次为唇口圆角半径、气面唇角、安装过盈量、油面唇角、弹簧刚度。由此可见，油封唇口圆角半径对油封唇口最大接触压力和单位周长径向力的影响程度都为最大；气面角对单位周长径向力有较显著的影响；油面角对油封唇口最大接触压力有较强的影响，但对单位周长径向力影响较小；弹簧刚度对单位周长径向力和最大接触压力影响均较小。

(2)以最大接触压力和最小单位周长径向力为优化目标，获得了气门油封最优结构参数组合为：油面角α=43°，气面角β=23°，过盈量δ=0.1 mm，弹簧刚度k=0.792 N/mm，唇口圆角半径r=0.1 mm。优化后的气门油封最大接触压力比初始油封增加了85.61%，单位周长径向力降低了20.54%。

(3)文中以气门油封为研究对象，进行结构参数对唇口接触特性研究与优化，研究方法同样适用于其他不同规格的油封，对油封的结构设计和优化都能起到一定的参考意义。