表面织构形貌参数影响润滑性能的三维CFD分析*

王剑豪 严志军 申子玉 潘新祥,2

(1.大连海事大学轮机工程学院 辽宁大连 116026；2.广东海洋大学海洋工程学院 广东湛江 524088)

近年来，表面织构技术被认为是一种改善摩擦学性能的有效手段[1-2]，并在滑动轴承[3]、机械密封[4]、内燃机缸套-活塞环[5]、切削刀具[6]等领域得到了广泛的应用。合理设计的表面织构具有减摩、抗磨和提高承载力等特性[7]，已成为当前摩擦学研究的一大热点。

HAMILTON等[8]最先提出利用表面微凸体作为一个微流体动压润滑轴承产生附加动压润滑效果的理论。随后ETSION[9]在表面织构技术的应用方面进行了大量的理论与实验研究，并认为圆形微凹坑的润滑性能与凹坑的直径、分布密度以及深径比等参数密切相关。YU等[10-11]结合实验和数值模拟对比研究了圆形、三角形、正方形和椭圆形的微凹坑的流体润滑效果，发现在相同的面积密度下，长轴垂直于润滑油流动方向的椭圆形织构能产生最大的承载能力。

典型的微织构形貌一般为圆形或正方形的凹坑，但随着微织构加工技术的发展(如激光加工技术)，学者们得以制备和研究更为复杂的三维形貌[2]。LI等[12]利用激光加工技术在锥形模具表面加工了4种不同密度的人字形微织构，发现当织构密度为9.5%时，表面摩擦因数最小且稳定。NANBU、LIU等[13-14]则关注微凹坑底面形貌的优化，发现织构底部具有微楔形或微阶梯形的凹坑能提高承载能力。SHEN和KHONSARI[15]提出了一种基于SQP算法的数值纹理优化方法，研究了推力轴承表面织构的最优形貌，发现梯形织构和前端平坦的人字形织构的承载能力最好，并认为这是由于织构的汇流效应在前端累积了高压的原因。

在不同接触类型和摩擦工况的条件下，织构参数的选择往往难以形成统一的结论[1-2]。因此在设计织构时，需要更加丰富的理论基础作为指导。WANG等[16]用Fluent软件求解二维的N-S方程，研究了推力轴承槽型织构的内部流场特性，并用空化和涡流的共同效应来分析织构对承载力和摩擦力的影响。但是，二维模型只能模拟沟槽织构，无法研究织构表面形状的影响。LI等[17]建立了圆形微凹坑的数值模型，通过速度场分析了凹坑内涡流的影响，但该研究未考虑空化效应。

目前，针对微织构形貌参数的模拟研究很少有建立考虑空化的三维CFD模型，且织构的形貌较为单一。因此本文作者在考虑空化效应的条件下，利用ANSYS-Fluent软件对表面微织构进行三维数值模拟，研究微织构的深度、面积密度以及表面形状对润滑性能的影响规律，为表面微织构合理的设计提供理论依据。

1 计算模型和计算方法

1.1 几何模型

图1(a)、(c)为织构化的平面滑动摩擦副示意图，其中下壁面固定，且布置有正方形的凹坑阵列，上壁面相对于下壁面做水平运动，滑移速度为U。如图1(b)、(d)所示取单个织构的正方形流体域作为计算单元，流体域的边长为L，织构的边长为a，最小油膜厚度为h0，织构的深度为h1。计算单元x轴的两端采用周期性边界条件，y轴两端为大气压力。

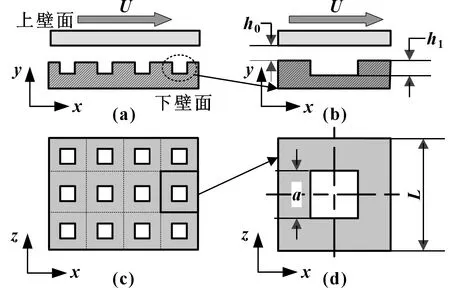
图1 正方形织构的阵列和计算单元

定义量纲一织构深度D为

D=h1/h0

(1)

定义织构密度ρt为

(2)

式中:St为织构面积;Sd为计算单元面积。

1.2 数值模型和求解设置

文献[18]中指出，惯性项对表面织构区域流动的求解具有重大的影响，而Reynolds方程忽略了惯性项，并不能很好地预测微织构对于承载的作用。因此，文中基于Fluent多相流空化模型，依据N-S方程建立了微织构流体域的三维数值模型并求解。同时做出如下假设：①润滑介质为不可压缩的牛顿流体，不计体积力的影响；②流体流动为定常流动，且壁面流体流速与壁面运动速度相同；③摩擦副表面无形变；④其余N-S方程的基本假设。

基于以上假设，N-S方程在x、y、z方向的展开式为

(3)

(4)

(5)

连续方程：

(6)

式中:ρ为润滑油密度;u、v、w分别为x、y、z向的流速;p为油膜压力;η为润滑油黏度。

(7)

(8)

(9)

式中:Fy为法向承载力;p(x,z)为上壁面的压力分布;F0为参考作用力;p0为大气压力;Fx为切向摩擦力;τ′为剪切力。

采用Fluent17.0三维双精度求解器进行仿真计算，流体状态选择k-ε湍流模型。空化的模拟采用Mixture多相流模型，并选用Schnerr-Sauer空化模型。压力速度耦合用Coupled方式，动量项和能量项均选为Quick。为了便于计算，其余条件均为默认。文中相关计算参数如表1所示。

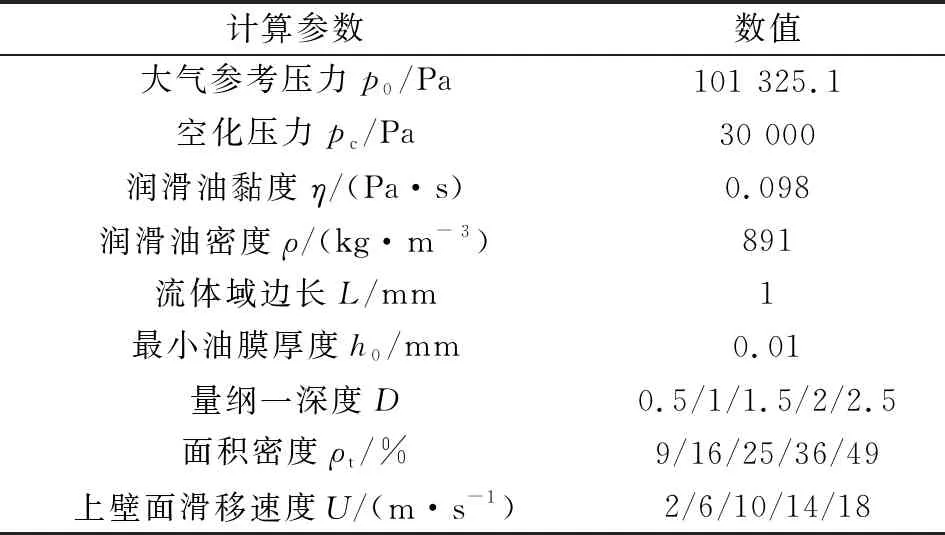
表1 计算参数

1.3 网格划分和模型验证

文中用ANSYS mesh软件对计算模型进行网格划分。体网格由x-z平面上的面网格向y轴方向扫掠生成。面网格选用三角形网格，以便适应各种表面几何形状，油膜厚度和织构深度的总扫掠层数不少于12。并且通过网格无关性试验对比发现，全局面网格尺寸设定为8 μm，织构区及其进出口区域的网格加密为4 μm是最为经济的网格划分方法。如图2所示，采用文中的计算方法所得的结果与文献[16]基本吻合，表明了文中计算方法的正确性。

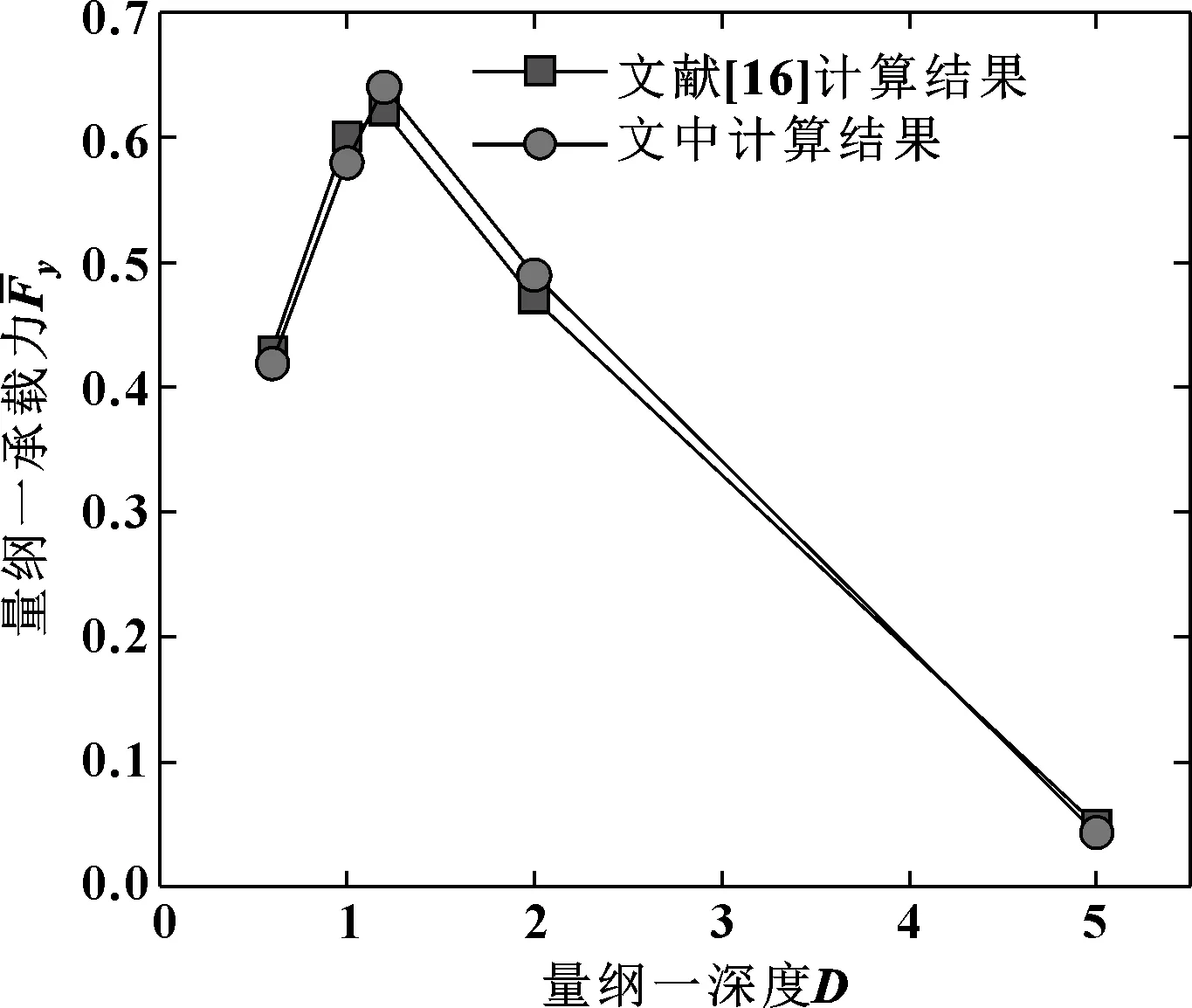
图2 文中方法计算结果和文献[16]结果对比

2 计算结果及分析

2.1 油膜上壁面的典型压力分布

如图3和4所示，上壁面从左向右运动(文中默认)，由于微凹坑织构的存在，在织构的进出口会分别形成低压区和高压区，考虑空化与未考虑空化效应时，上壁面压力分布有明显的区别;在未考虑空化效应时，低压区和高压区几乎为对称分布。如图4所示，在润滑油流入微凹坑之前，压力逐渐下降，在微凹坑入口A处达到一个负的最小值；进入微凹坑后，压力逐渐上升，且在出口位置B达到最大值；流出微凹坑之后，压力又呈下降趋势。最小压力和最大压力的绝对值相差不大，无法体现出织构的存在对承载力的提升作用。考虑空化效应时，增压区的面积远大于负压区的面积。这是因为在微凹坑入口A附近，压力下降到空化压力便不再下降，并在微凹坑内维持一定范围的空化压力后，压力上升，同样在出口位置达到最高压力值，导致最大压力值远大于最小压力值。另外，由于在周期性边界下，润滑油流动方向上的计算域会相互影响，产生压力累积的效果，使得每个计算域的入口和出口压力都大于大气压力。所以，在流体动压润滑条件下，空化现象的存在是微织构提升油膜承载力的主要原因之一。

图3 考虑空化和未考虑空化的上壁面典型压力分布(U=6 m/s)

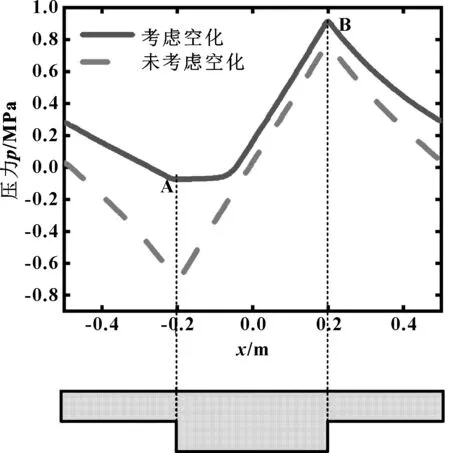
图4 中心截面上的压力分布

2.2 微织构深度对润滑性能的影响

为研究微织构深度对摩擦副润滑性能的影响，取正方形织构的面积密度为16%，上壁面的滑移速度为6 m/s。从图5中可以看出，随着织构深度的增加，油膜对上壁面产生的量纲一承载力呈先增大后减小的趋势，而摩擦力变化相对较小，导致摩擦因数与承载力成反比关系。在文中研究范围内，量纲一深度D=1的织构能提供最大承载力和最小的摩擦因数，润滑性能最优。

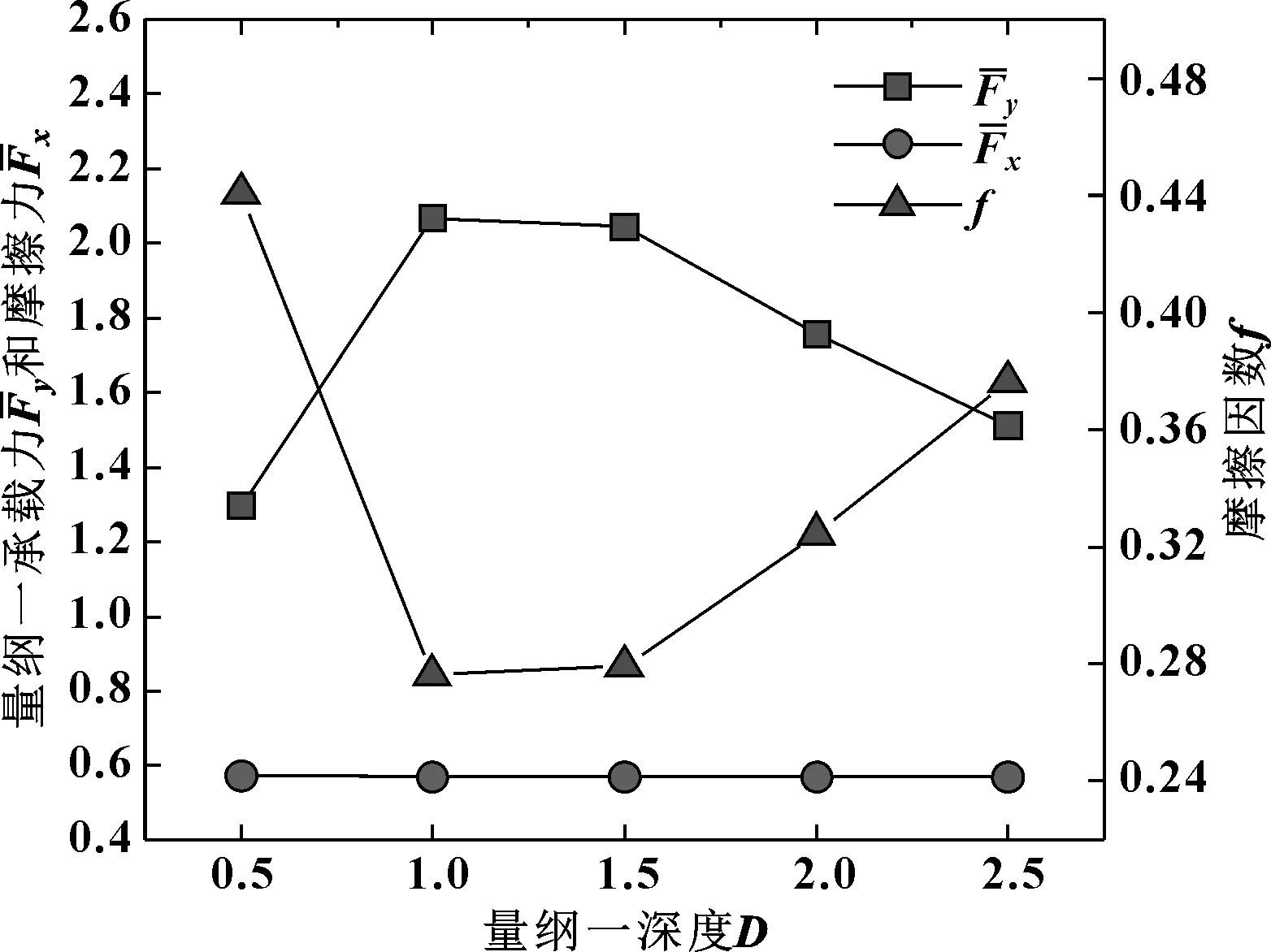
图5 不同深度织构下的承载力、摩擦力和摩擦因数

关于存在最优织构深度的原因，文献[17]中通过分析速度场发现了涡流的存在，并给出如下解释：微凹坑的深度增加，会使楔形效应增强，提高流体动压性能，但另一方面会产生涡流现象导致能量耗散，削弱流体动压承载性能。因此织构深度会存在一个最优值，使得微坑单元的动压承载性能最强。而文献[19]中通过摩擦实验发现了全润滑条件下最优织构深度的存在，并观察到织构深度增加会导致空化面积的减小，从而影响润滑性能。

为了进一步研究空化效应和涡流效应的影响，图6给出不同深度织构的中心截面上的空化气相图和流线图。流体域在y轴方向放大了10倍，以便观察。当D=0.5时，织构凹坑内空化区的占比最大，流线较为均匀有序，且不存在涡流现象；当D=1时，空化区的占比减小，同时在空化区的下游形成了涡流区；当D=1.5时，空化区的占比进一步减小，涡流区增大。这说明织构深度的增加对流体动压性能的削弱，是由于空化区减小和涡流区增大的综合作用。

图6 不同深度织构下的中心截面流场和空化气相图(x∶y=1∶10)

不同速度条件下的最优量纲一深度如图7所示。其中最优量纲一深度是通过比较不同深度织构的润滑性能得出的，深度最优时，摩擦因数最小。当上壁面滑移速度在6～14 m/s之间时，最优深度为1；当速度减小为2 m/s时，最优深度为1.5；而当速度增大到18 m/s时，最优深度为0.5。随着速度的增加，织构的最优深度有减小的趋势。这是因为速度的增加有利于楔形效应的增强[17]，使得较浅的织构也能提供足够的流体动压性能，同时又可以减小涡流的削弱作用。

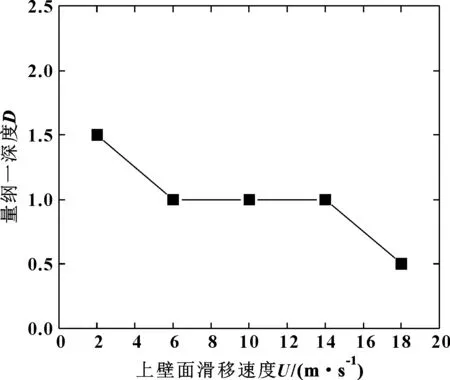
图7 不同速度下的最优量纲一深度

2.3 微织构密度对润滑性能的影响

固定织构深度D=1，上壁面滑移速度为6 m/s，不同面积密度织构的承载力、摩擦力和摩擦因数如图8所示。随着织构面积密度的增加，油膜对上壁面产生的量纲一承载力呈先增大后减小的趋势，量纲一摩擦力则逐渐减小，但变化幅度没承载力大。摩擦因数随着面积密度的增大逐渐减小，当织构密度达到36%后开始回升。在文中的研究条件下，织构面积密度为25%时，油膜的承载力最大，摩擦因数最小。

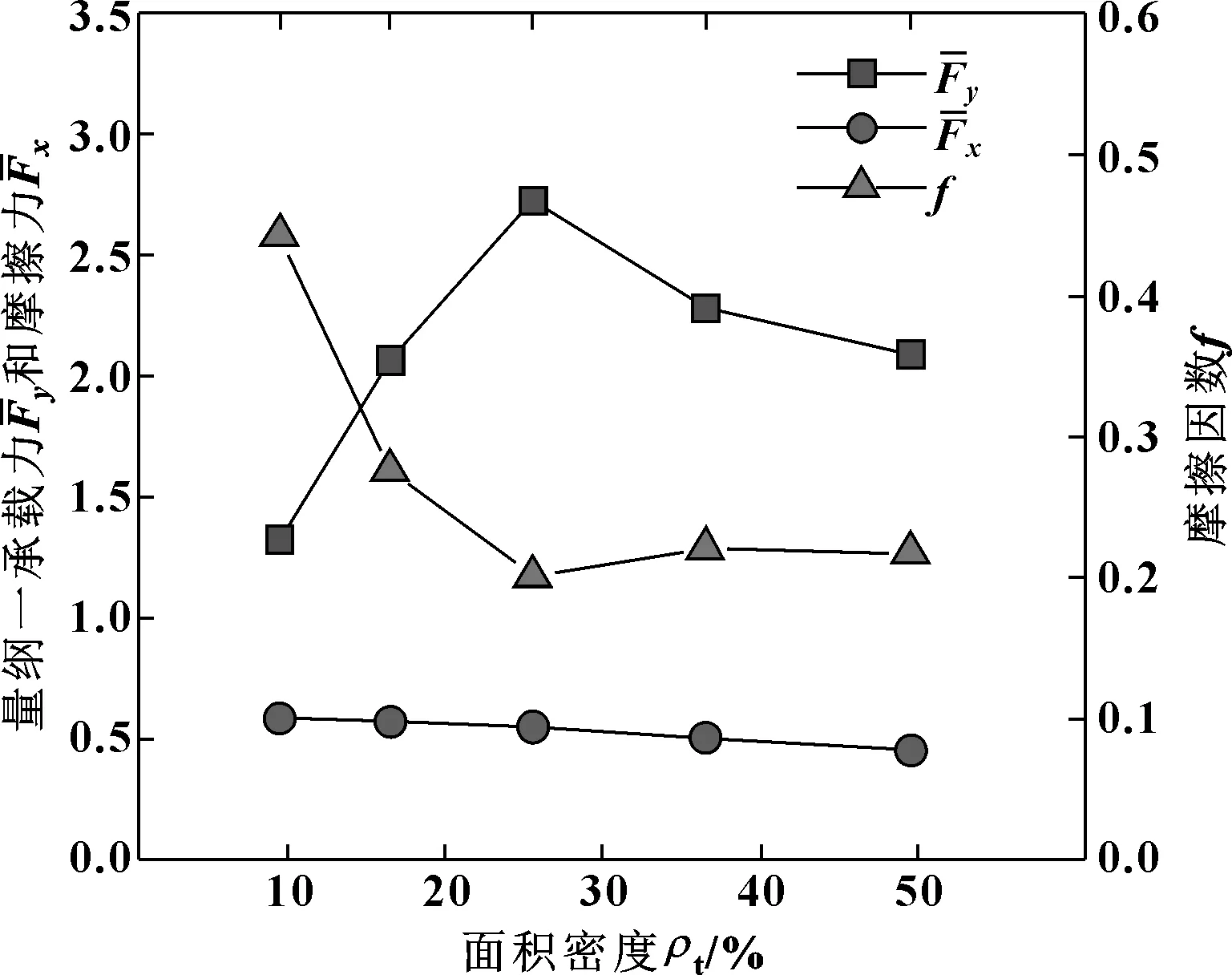
图8 不同面积密度织构的承载力、摩擦力和摩擦因数

如图9所示，随着织构面积密度的增大，上壁面中心线上的压力峰值也呈先增大后减小的趋势，面积密度为25%时峰值最高。另外，面积密度的增加也会导致出口截面的边长变大，这意味着织构出口处的收敛区更大，能够累积产生更强的流体动压效果。但是，织构的面积密度不是越大越好，当密度为36%时，承载力开始下降。这是因为在周期性边界条件下，流动方向上排列的织构会相互影响，流体从前一个织构的出口收敛截面流出后，就会进入后一个织构的进口发散截面。面积密度过大会导致发散区和收敛区过于接近，在收敛区累积的高压峰值会受发散区的影响而加快下降速度。

而量纲一摩擦力的减小是因为空化区的增大。从图9中可以看出，织构面积密度越大，上壁面中心线上的压力值为空化压力的区域也越大，说明流体域中析出了更多气体。由于气体的黏度远小于润滑油[16]，使得量纲一摩擦力也随之减小。

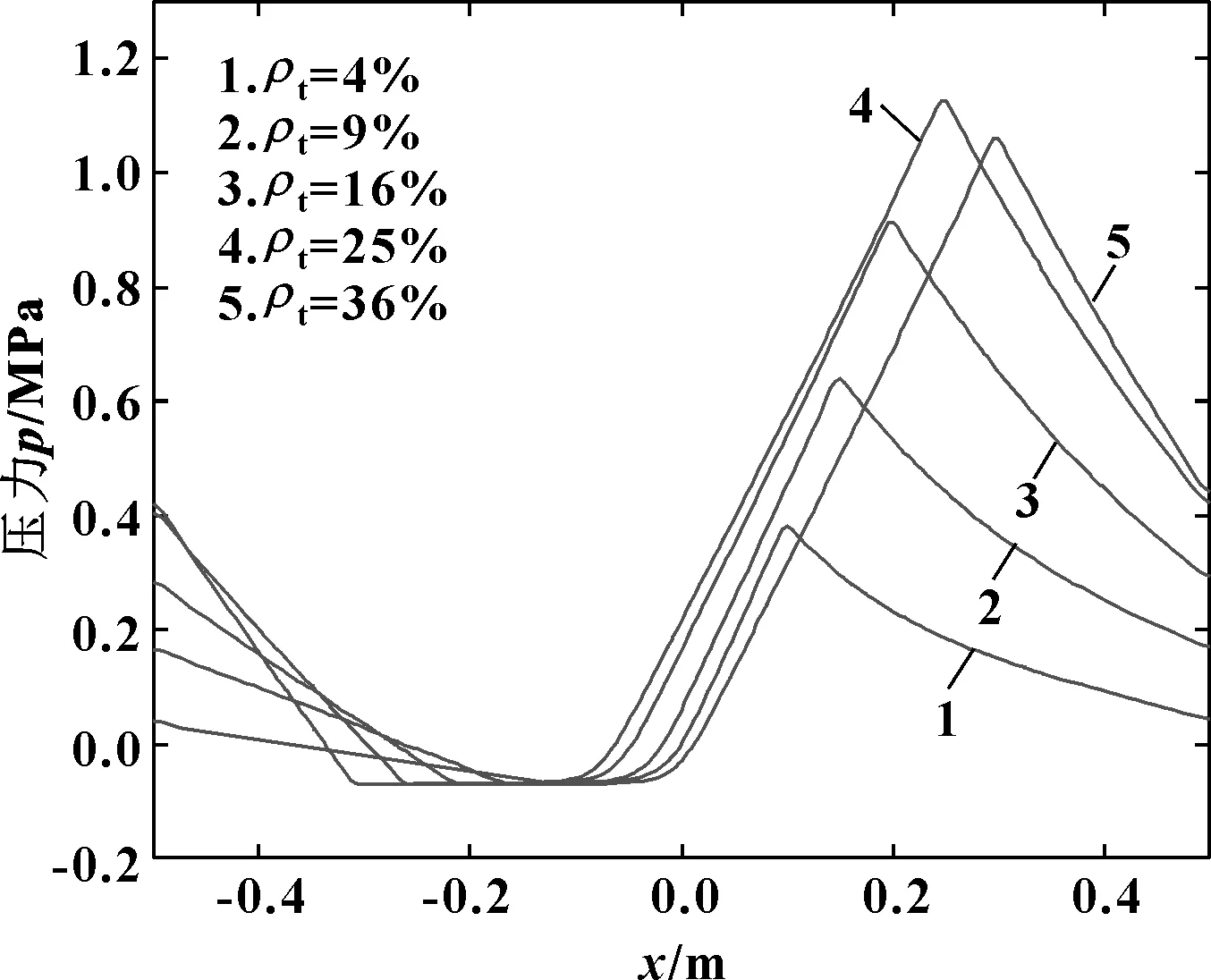
图9 不同密度织构下上壁面中心线压力分布

不同速度下的最优面积密度如图10所示。当速度从2 m/s增加到6 m/s时，最优面积密度从49%下降至25%，这是因为速度的增大会使得增压区向后端扩张，织构之间的抑制作用开始体现。同时单个织构产生的流体动压也会随速度增大，当速度达到10 m/s后，最优面积密度稳定在了36%，单个织构的增压效果和织构之间的抑制作用达到了平衡。

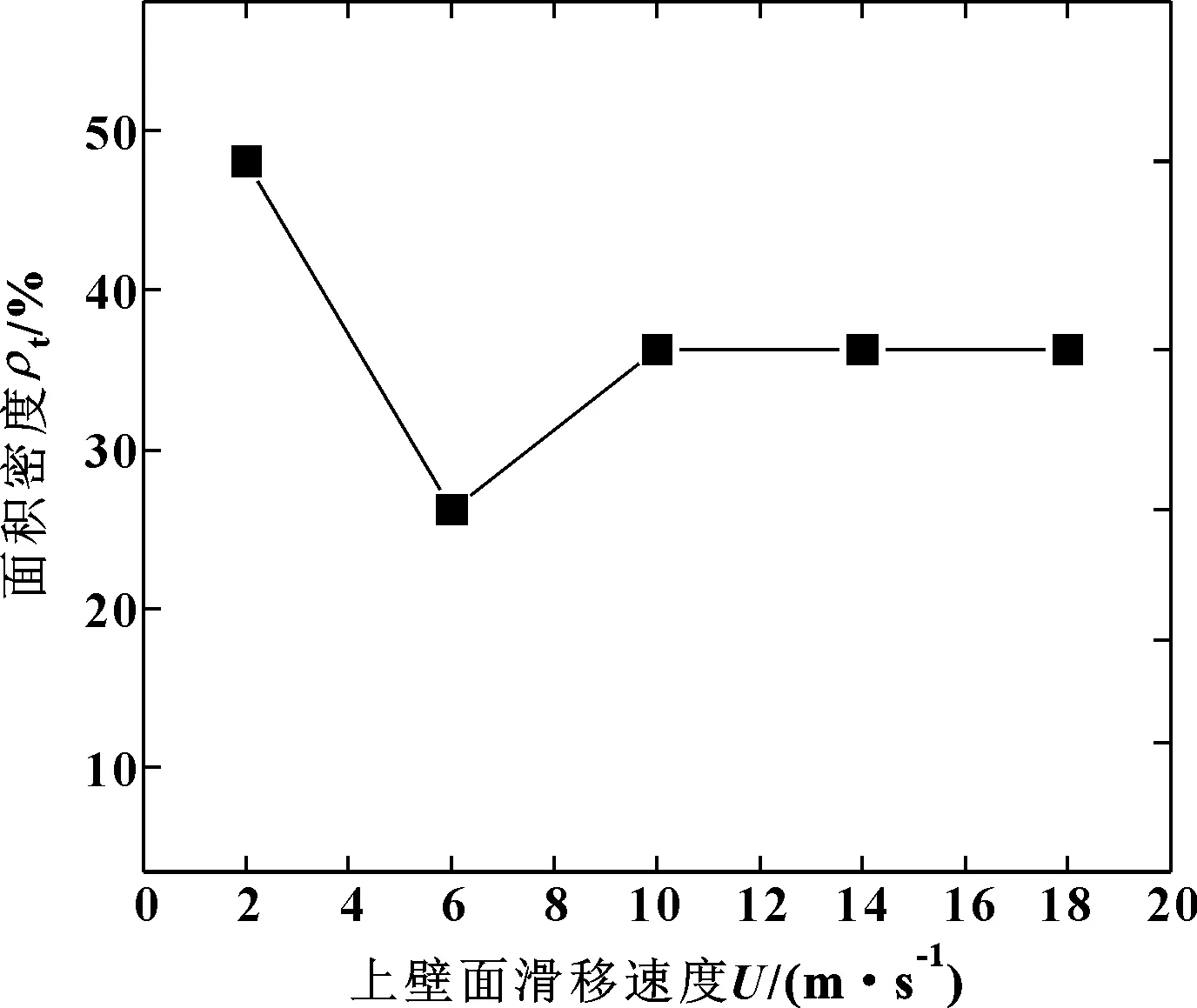
图10 不同速度下的最优面积密度

2.4 微织构形状对润滑性能的影响

量纲一深度为1，面积密度为16%，速度为6 m/s的条件下，不同表面形状织构的上壁面压力分布如图11所示。图中黑色区域的压力值为空化压力。达到空化压力值的区域越大，空化现象越剧烈，空化区也越大。T1和T2为分布方向不同的等腰梯形织构，流体从梯形较长的底边流入织构T1，从梯形较短的底边流入织构T2。从图中可以看出，由于织构的汇流作用，织构T1的出口区域累积了更高的油膜压力，入口处的空化压力区相对较小；由于织构T2的宽度在流体流动方向不断增大，具有发散的作用，导致织构入口位置的空化压力区较大，而在出口区域累积的压力较低。S2为正方形织构，流体从正方形的一个角流入，从与之相对的另一个角流出。织构S2同时具备发散和汇流的作用，在入口区容易达到空化压力，而在出口区的尖端会累积高压。P1为平行四边形织构，也同时具备发散和汇流的效果，另外高压峰值区和低压空化区发生了偏移，可以降低前后织构之间的抑制作用。

图11 不同形状织构的上壁面压力分布

当速度为6 m/s时，不同形状织构的量纲一摩擦力和承载力如图12所示。其中S1为图1中的正方形织构。由图12可见，不同形状织构对量纲一摩擦力的影响可以忽略，量纲一承载力越大，表示摩擦因数越小，摩擦副的润滑性能越好。

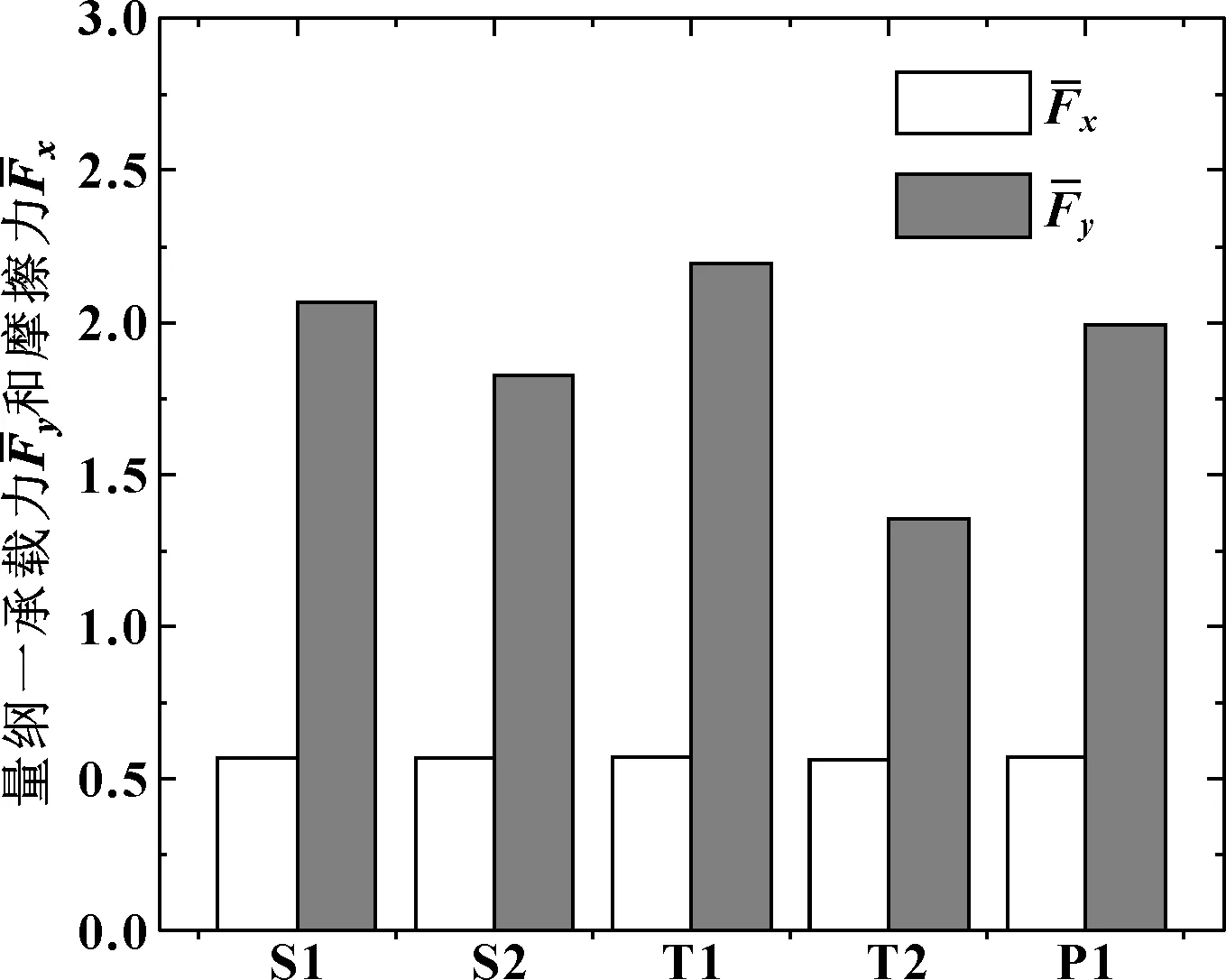
图12 不同形状织构的承载力和摩擦力

在不同速度条件下，织构表面形状对量纲一承载力的影响如图13所示。随着速度的增大，不同形状织构的量纲一承载力都增大。当速度大于10 m/s时，具有汇流作用的织构T1、S2和P1的量纲一承载力要优于织构S1，且速度越大对承载力的提高越显著。当速度为18 m/s时，同时具备汇流和发散效果的织构S2和P1所提供的承载力要优于织构T1，另外织

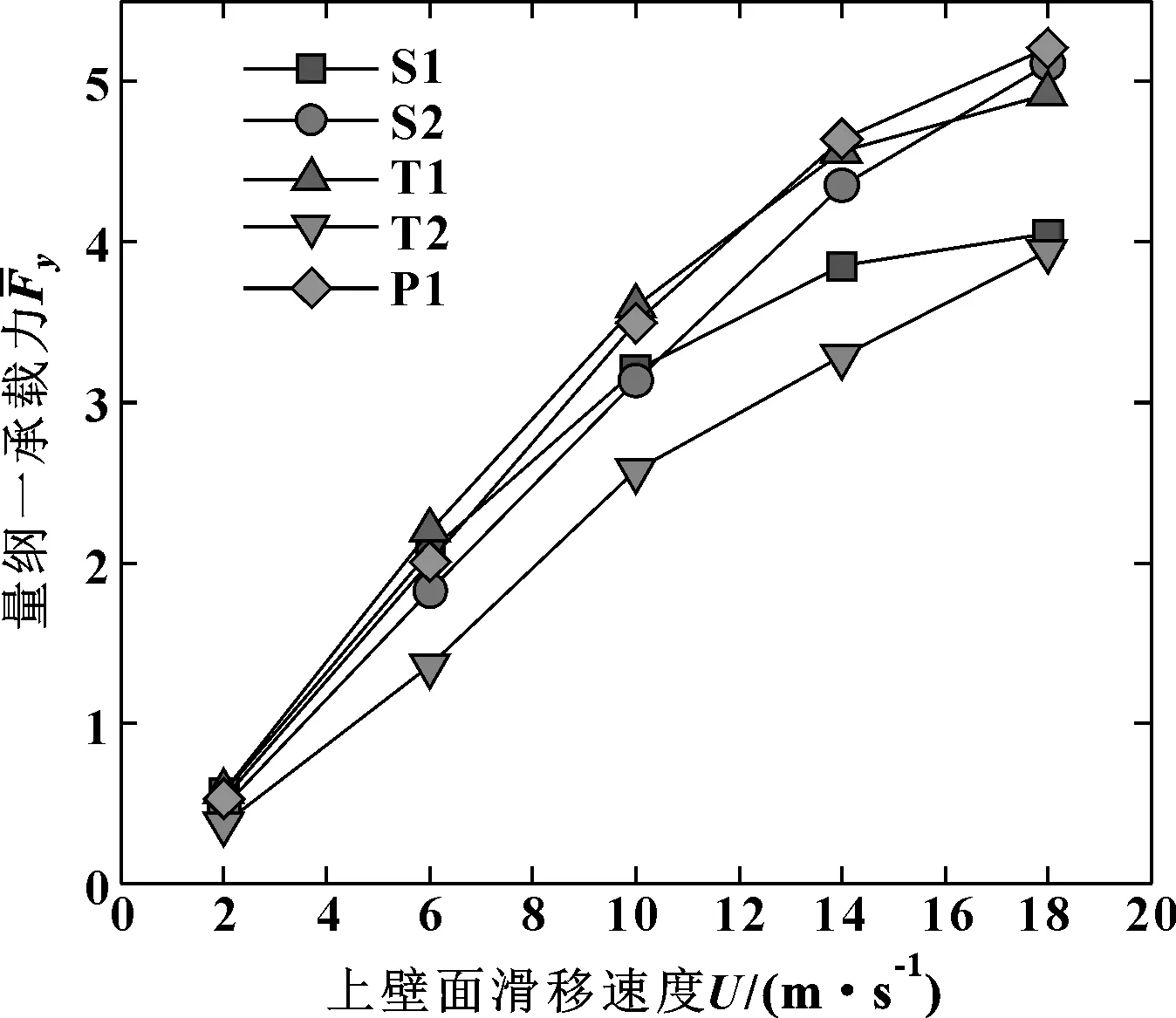
图13 不同速度条件下织构表面形状对承载力的影响

构P1还能降低前后织构之间的抑制作用，所以织构P1提供的承载力比S2大。在各个速度条件下，织构T2提供的承载力均最小。织构T2只有发散的效果，入口位置的空化压力区较大。这说明空化效应虽然是织构产生承载力的主要原因之一，但织构产生的空化区不是越大越好。

3 结论

(1)空化现象的存在是微织构提升油膜承载力的主要原因之一，在模拟研究中不可忽略。

(2)在文中研究的参数范围内，随着织构深度(面积密度)的增加，油膜的承载力先增大后减小，摩擦因数先减小后增大。即织构存在最优的深度和面积密度，使得流体动压润滑性能最优。随着上壁面滑移速度的增大，织构的最优深度有减小的趋势，而最优面积密度趋于稳定。

(3)设计具有汇流作用的织构表面形状可以进一步提高油膜的承载力，改善润滑效果，且速度越大，提升效果越明显。