密封环圆台型织构化粗糙表面对润滑性能的影响*
2021-07-23樊智敏马瑞磷
樊智敏 马瑞磷 江 峰
(青岛科技大学机电工程学院 山东青岛 266100)
机械密封是一种广泛应用于工业领域的密封装置,它主要由动环和静环组成,两环之间形成一层液膜可以减少端面磨损,同时液膜需要足够薄来防止过度泄漏。许多学者采用表面织构的方法来提高机械密封的性能,近几年,表面织构技术已经成功地应用于轴承和密封领域[1-2]。机械密封润滑膜厚度为微米级,端面粗糙度通常为相同数量级或高一个数量级,因此表面粗糙度对密封性能的影响不容忽视[3-4]。
陈汇龙等[5]采用 Gauss 概率分布模型描述密封端面粗糙度,研究了动压型机械密封端面粗糙度对密封润滑性能的影响。吕祥奎等[6]基于 Gauss 分布函数和指数自相关函数,研究了金属垫片密封结构的粗糙表面特征参数和接触压力对密封结构泄漏率的影响。上述研究只研究了单一粗糙度,未考虑织构和粗糙度共同作用的影响。马晨波等[7-8]考察了粗糙度参数对织构表面摩擦学性能及最优织构参数的影响规律,进而建立考虑粗糙度影响的最优参数设计模型对表面织构进行摩擦学设计。陈文杰等[9]考虑润滑液膜的宏微观空化效应和微凸体的接触作用,研究了具有不同粗糙度特征的圆孔型织构化机械密封的摩擦学特性和密封性能。上述研究考虑了织构和粗糙度共同作用的影响,但织构类型均采用圆形织构,存在几何织构形状考虑不全面的问题。
本文作者以动静密封环接触面之间的润滑膜为研究对象,考虑粗糙度的影响,建立在流体动压润滑状态下圆台型表面织构的数学模型,对不同织构参数、不同粗糙度参数、不同工况下润滑膜压力大小及分布情况进行了研究,旨在提高动静环接触面的润滑密封能力。
1 几何模型
图1为考虑粗糙度参数时圆台织构微单元的模型图。构建如图1所示坐标系。
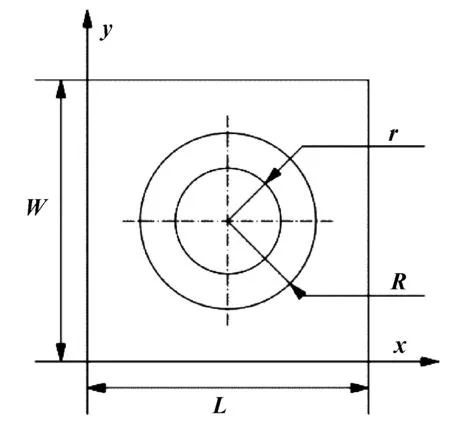
图1 圆台织构微单元模型
其中,L、W分别表示微单元在x、y坐标上的长度(假设微单元为正方形),圆台织构外径为R,内径为r,深度为hp。为便于计算分析,假设凹坑织构位于微单元的中心位置。
粗糙织构表面如图2所示,U为摩擦副表面相对运动方向,织构位于下表面,截面轮廓为梯形。
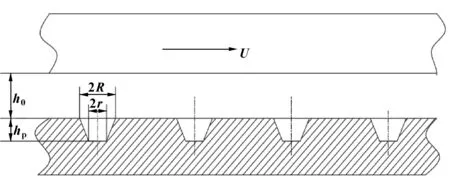
图2 粗糙织构表面模型
2 数学模型
2.1 建立Reynolds方程
稳态流体动力润滑状态下Reynolds方程可以表示为
(1)
式中:p为润滑膜压力;η为运动黏度;ρ为密度;x和y分别为横和纵坐标;h为润滑膜厚度;U为下表面沿x方向上的运动速度。
2.2 膜厚方程
对单个圆台型微凹坑织构建立坐标系,如图1所示。假设圆台型凹坑内任意一点(x,y)到凹坑底面中心的距离为s,则:
(2)
不考虑粗糙度影响时,(x,y)的膜厚方程表达式为
(3)
假设粗糙度函数可近似用余弦函数来表示,则:
(4)
式中:wf为粗糙峰峰高;wb为粗糙峰波长。
综合考虑织构与粗糙度的影响时润滑膜厚度表达式为
h(x,y)=h1(x,y)-R(x,y)
(5)
2.3 边界条件
图3所示为单个凹坑栏示意图。其中,x轴为运动方向,凹坑栏内微凹坑数为Np。
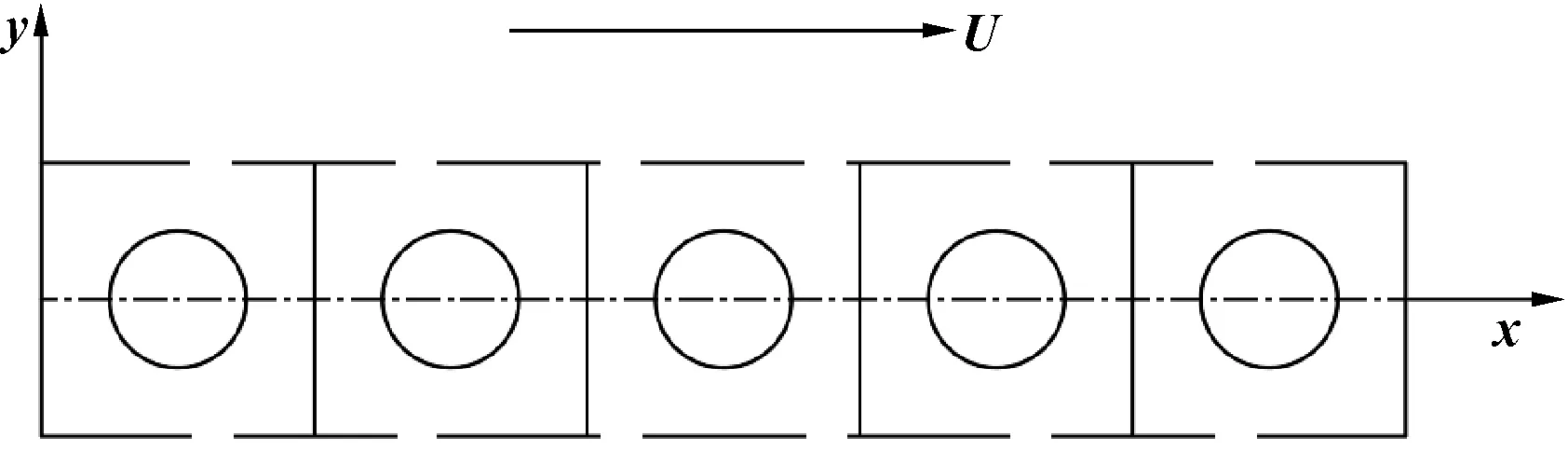
图3 单个矩形凹坑栏示意
沿x方向,滑块两端的边界压力为环境压力p0;沿y方向,润滑膜压力呈周期性分布,即:
(6)
2.4 润滑膜的平均压力
单个微坑内润滑膜的平均压力表达式为
(7)
式中:lx为滑块的长度,lx=LNp。
2.5 量纲一化
定义如下量纲一化参数:
(8)
式中:X、Y为量纲一的直角坐标系;H为量纲一润滑膜的厚度;P为量纲一润滑膜的压力;p0为大气压;Rp为量纲一圆台织构外径。
式(9)为量纲一化Reynolds方程:
(9)
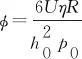
任意一点的量纲一化膜厚方程可由式(10)表示:
(10)
将式(8)代入式(4)得微凹坑栏外表面粗糙度的量纲一化方程为
(11)
式中:Wf=wf/h0,Wb=wb/lx。
将式(8)代入式(5)可得微凹坑织构化粗糙表面润滑膜的量纲一化膜厚方程:
H(X,Y)=H1(X,Y)-R(X,Y)
(12)
从而,量纲一化边界条件为
(13)
单个凹坑栏内润滑膜平均量纲一压力为
(14)
3 数值计算
3.1 有限差分法求解Reynolds方程
对式(9)采用中心差分格式进行离散化得到最终的计算公式:
APi+1,j+BPi-1,j+CPi,j+1+DPi,j-1-EPi,j=F
(15)
其中,
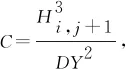
各节点润滑膜压力P(i,j)表达式为
(16)
3.2 松弛迭代法和收敛准则
由式(16)所给出各节点处的润滑膜压力表达式形成一组线性方程,采用超松弛迭代法进行求解,如式(17)所示。
(17)
式中:k为迭代次数;b为松弛因子,其中松弛因子大于1时为超松弛,小于1时为亚松弛[10]。
为了保证迭代的收敛速度,取b=1.2。计算精度的判定如式(18)所示,E为预先设置的误差限,取E=10-6。迭代收敛条件为
(18)
计算流程如图4所示。
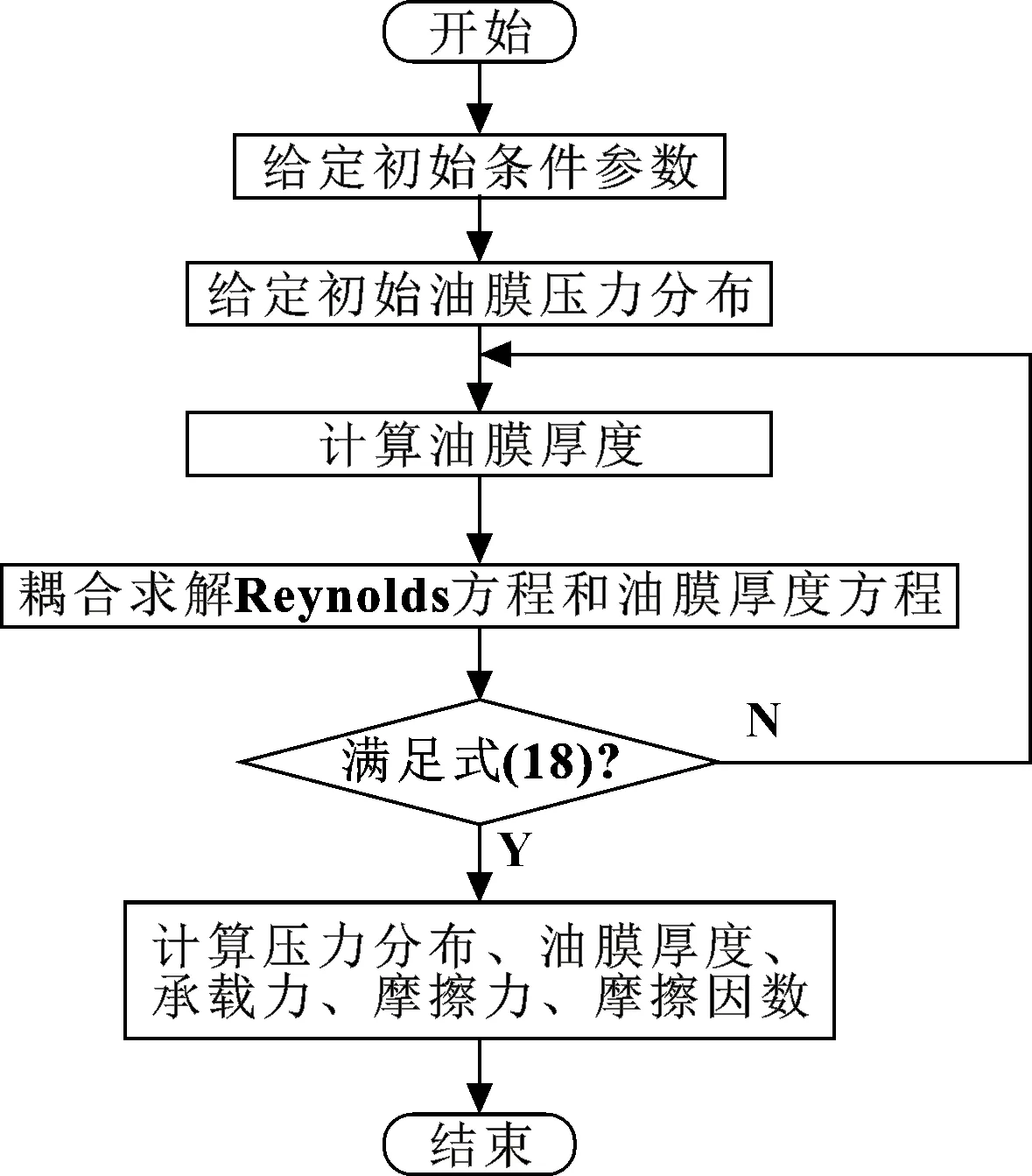
图4 计算流程
3.3 承载力计算
对于混合润滑状态,其总承载能力由两部分组成:润滑膜的承载力和粗糙峰的承载力[11]。润滑膜的承载力如下式:
(19)
在混合润滑状态下,采用Greenwood-William接触模型[12]求解粗糙峰的承载力,则平均接触压力载荷可表示为
pc=KE0F2(λ)
(20)
式中:K=5.318 7×1010·σ2.5;F2(λ)是与粗糙峰高度的概率分布相关的参数;E0代表摩擦副材料的综合弹性模量。
可得到粗糙峰的承载力为
(21)
则润滑膜和粗糙峰的总承载力为
D=D1+D2
(22)
3.4 摩擦力与摩擦因数计算
粗糙度存在时的摩擦力也由两部分组成,即动压油膜产生的黏性剪切力[13-14]和粗糙峰之间的摩擦力。首先确定剪切力的表达式,再对剪切力积分即可求得摩擦副表面的摩擦阻力,其表达式为
(23)
粗糙峰之间的摩擦力可表示为
(24)
则总摩擦力如式(25)所示:
F=Fy+Fc
(25)
求得承载力和摩擦力以后,摩擦因数可以表示为
μ=F/D
(26)
4 数值结果及分析
文中粗糙织构表面数值模拟主要参数如表1所示。
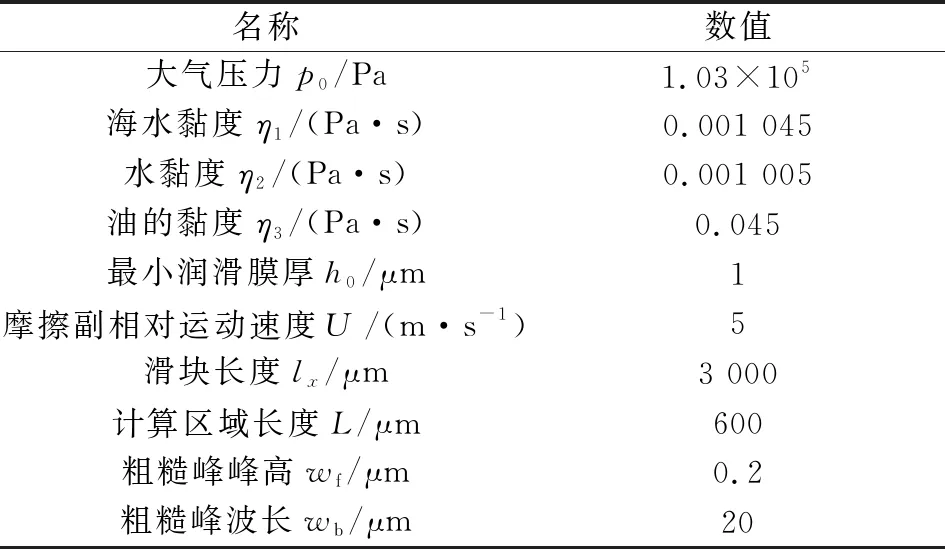
表1 粗糙织构表面数值模拟主要参数
图5、图6所示分别为海水为润滑介质、速度为5 m/s时粗糙织构表面的压力、膜厚分布规律。
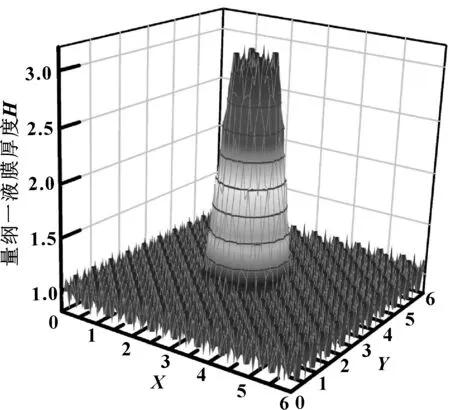
图5 量纲一润滑膜厚度分布
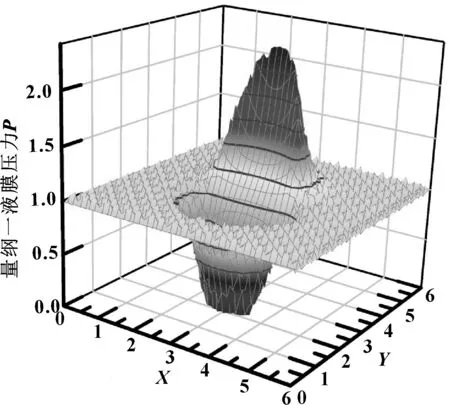
图6 量纲一润滑膜压力分布
4.1 验证分析
在水压2.5 MPa,弹簧压力0.15 MPa,转速3 000 r/min 工况下,使用模型进行仿真计算,通过解析计算的数据来验证仿真模型的正确性。由表2可见,膜压的仿真值与理论值误差率为0.8%,符合实际情况,验证了模型的可行性[15]。

表2 膜压的理论数据与仿真数据比较
4.2 圆台型织构几何参数对液膜压力的影响
通过对比3种类型的润滑介质(油、海水和水),综合分析不同润滑介质条件下,圆台型织构几何参数对液膜压力的影响。
4.2.1 织构间距对液膜压力的影响
取微凹坑织构深度为2 μm,其大、小半径分别为100、50 μm,摩擦副的相对运动速度为5 m/s。圆台型微凹坑间距对润滑膜量纲一平均压力的影响如图7所示。
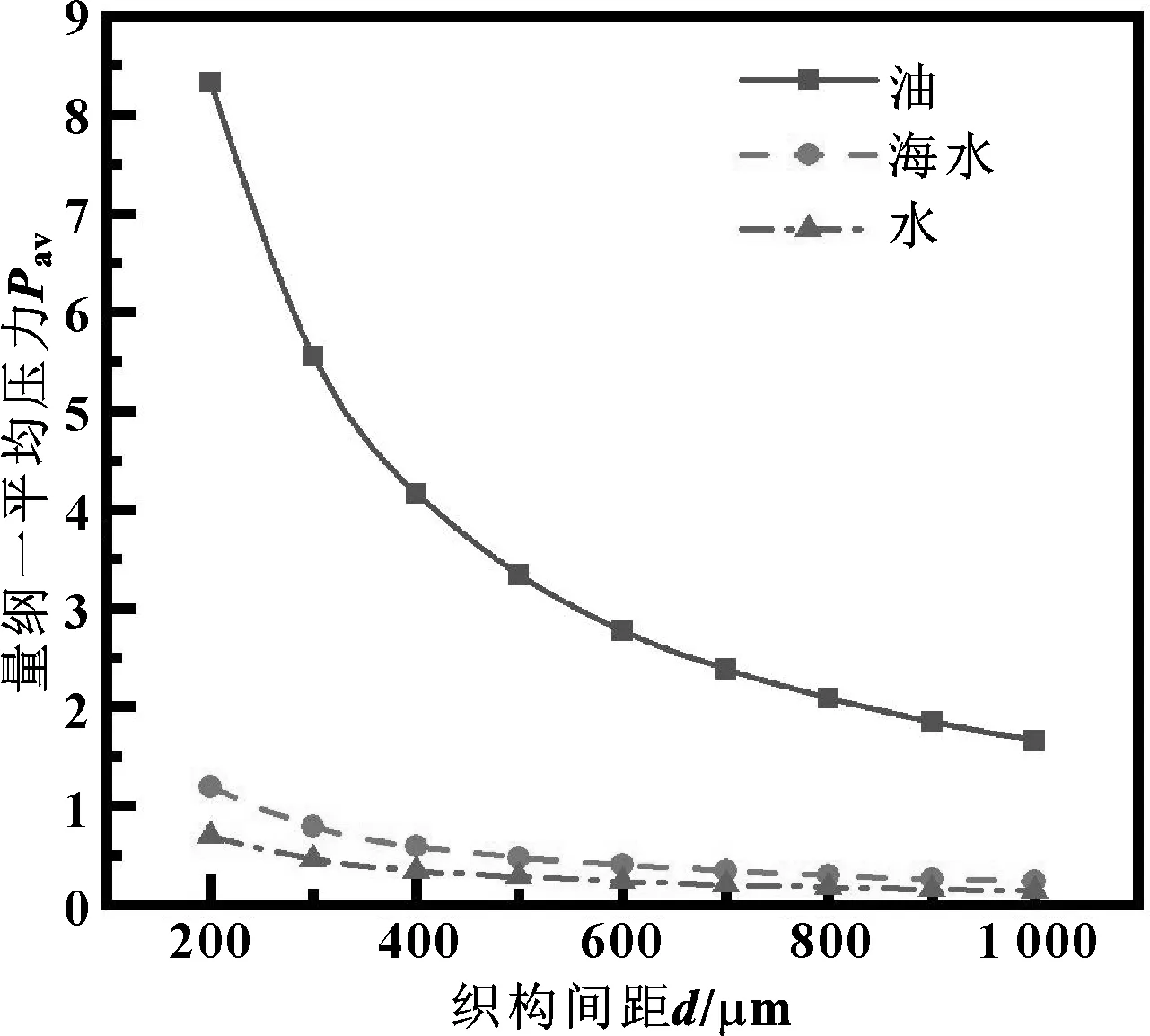
图7 微凹坑间距对量纲一平均压力的影响
由图7可知,随着微凹坑间距的增大,润滑膜的量纲一平均压力逐渐减小。当间距较大时,润滑膜的量纲一平均压力变化趋于稳定。当间距增加到600 μm,继续增大间距对平均压力几乎无影响。原因是计算域轴向长度一定,间距越大,织构的数量就越少,织构所产生的流体动压就越小。这与文献[16]中曲线趋势基本一致,说明文中方法可行。
4.2.2 织构深度对液膜压力的影响
取微凹坑织构间距为600 μm,其大、小半径分别为100、50 μm,摩擦副的相对运动速度为5 m/s。圆台型微凹坑深度对润滑膜量纲一平均压力的影响如图8所示。
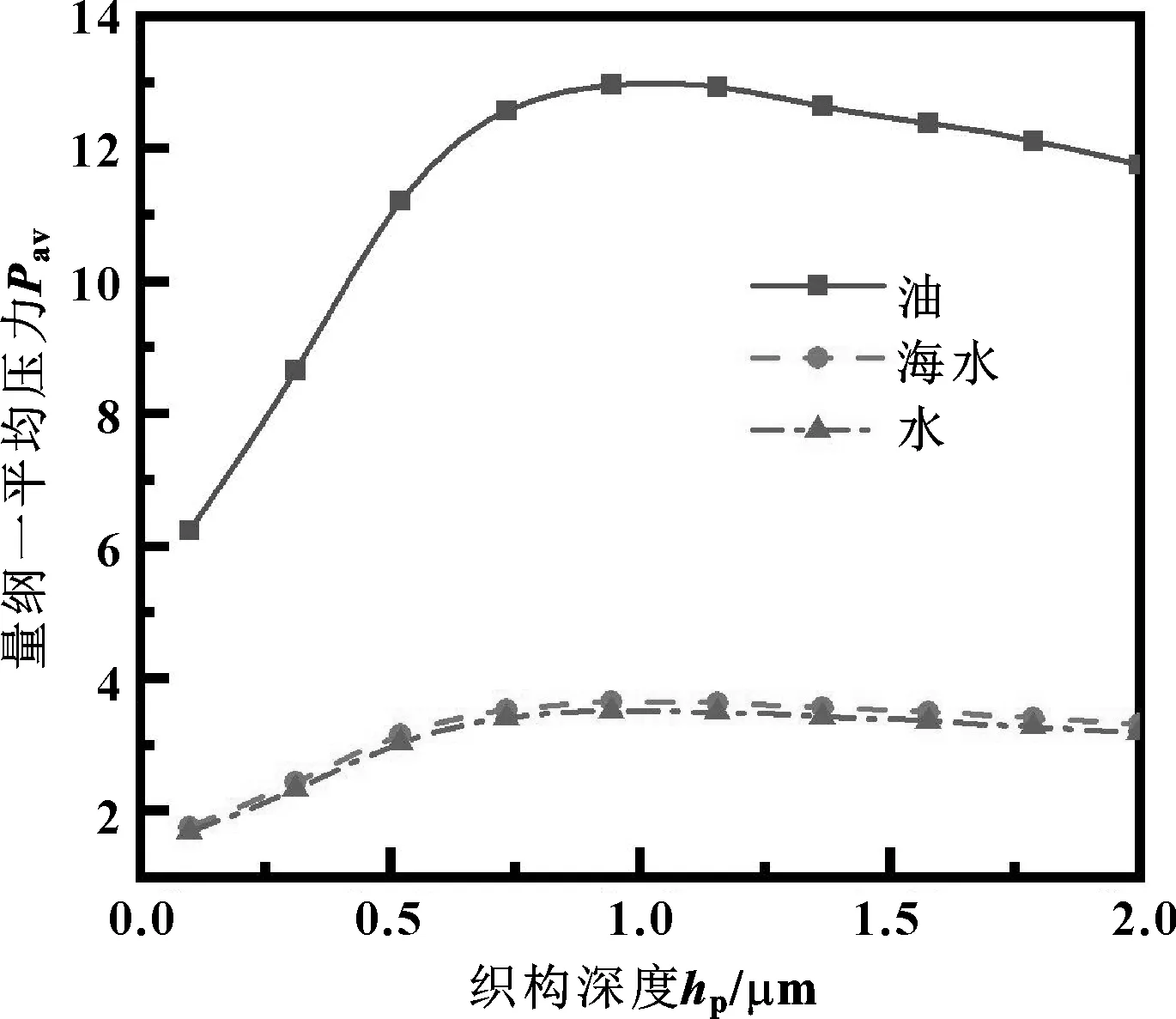
图8 微凹坑深度对量纲一平均压力的影响
由图8可知,量纲一平均压力随微凹坑深度的增大呈现先增大后减小的趋势,可以得出,存在一个最佳的织构深度,即织构深度取1 μm时,量纲一平均压力最大。这与文献[16]中曲线趋势基本一致。
4.2.3 织构大径对液膜压力的影响
取微凹坑织构间距为600 μm,织构深度为2 μm,小半径为50 μm,摩擦副的相对运动速度为5 m/s。圆台型微凹坑织构大径对润滑膜量纲一平均压力的影响如图9所示。
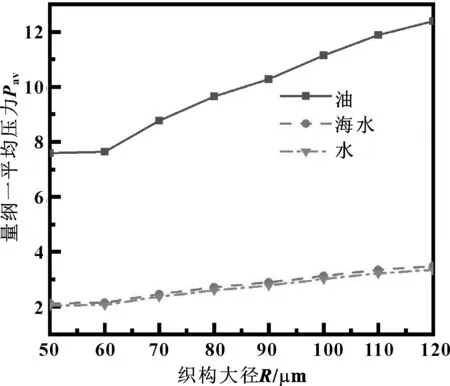
图9 微凹坑织构大径对量纲一平均压力的影响
由图9可知,织构小径不变时,量纲一平均压力随大径的增大而逐渐增大。当织构大径值趋近小径值时,即圆台型织构可近似看作底面半径为50 μm的圆柱型织构,此时量纲一平均压力最小,增长率也较小;当织构大径大于60 μm时,大径值每增加10 μm,油、海水、水润滑3种条件下量纲一平均压力分别增加0.69、0.19、0.18。
4.2.4 织构小径对液膜压力的影响
取微凹坑织构间距为600 μm,织构深度为2 μm,大半径为100 μm,摩擦副的相对运动速度为5 m/s。圆台型微凹坑织构小径对润滑膜量纲一平均压力的影响如图10所示。
由图10可知,织构大径不变时,量纲一平均压力随小径的增大而逐渐减小。当织构小径值趋近0时,即圆台型织构近似为圆锥型织构,此时量纲一平均压力最大,且平均压力的降低速率较小。当织构小径大于0时,小径值每增加10 μm,油、海水、水润滑3种条件下量纲一平均压力分别降低0.51、0.14、0.13。
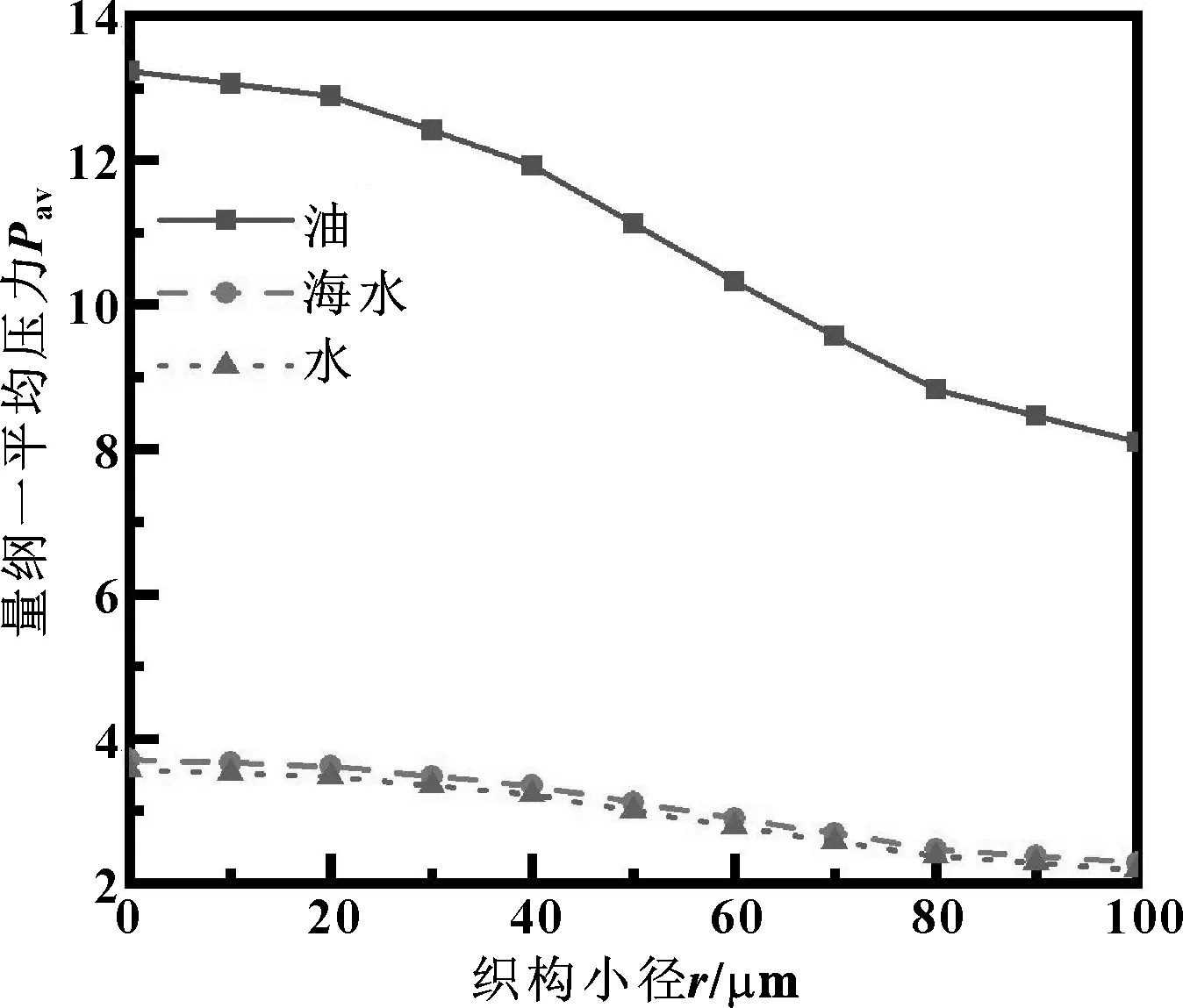
图10 微凹坑织构小径对量纲一平均压力的影响
综合图7—10结果,可以总结出,相同工况下,油作为润滑介质时的量纲一平均压力最大,海水次之,水作为润滑介质时的量纲一平均压力最小。原因是3种润滑介质的黏度不同[17],黏度越大,液膜动压效应越明显,因此量纲一平均压力越大;3种润滑条件下,量纲一压力变化趋势基本一致,说明最优织构参数不随润滑介质黏度的变化而变化。
4.3 余弦模型粗糙峰的影响
4.3.1 粗糙峰峰高对液膜压力的影响
图11示出了不同织构深度时,粗糙度峰高对平均压力的影响。
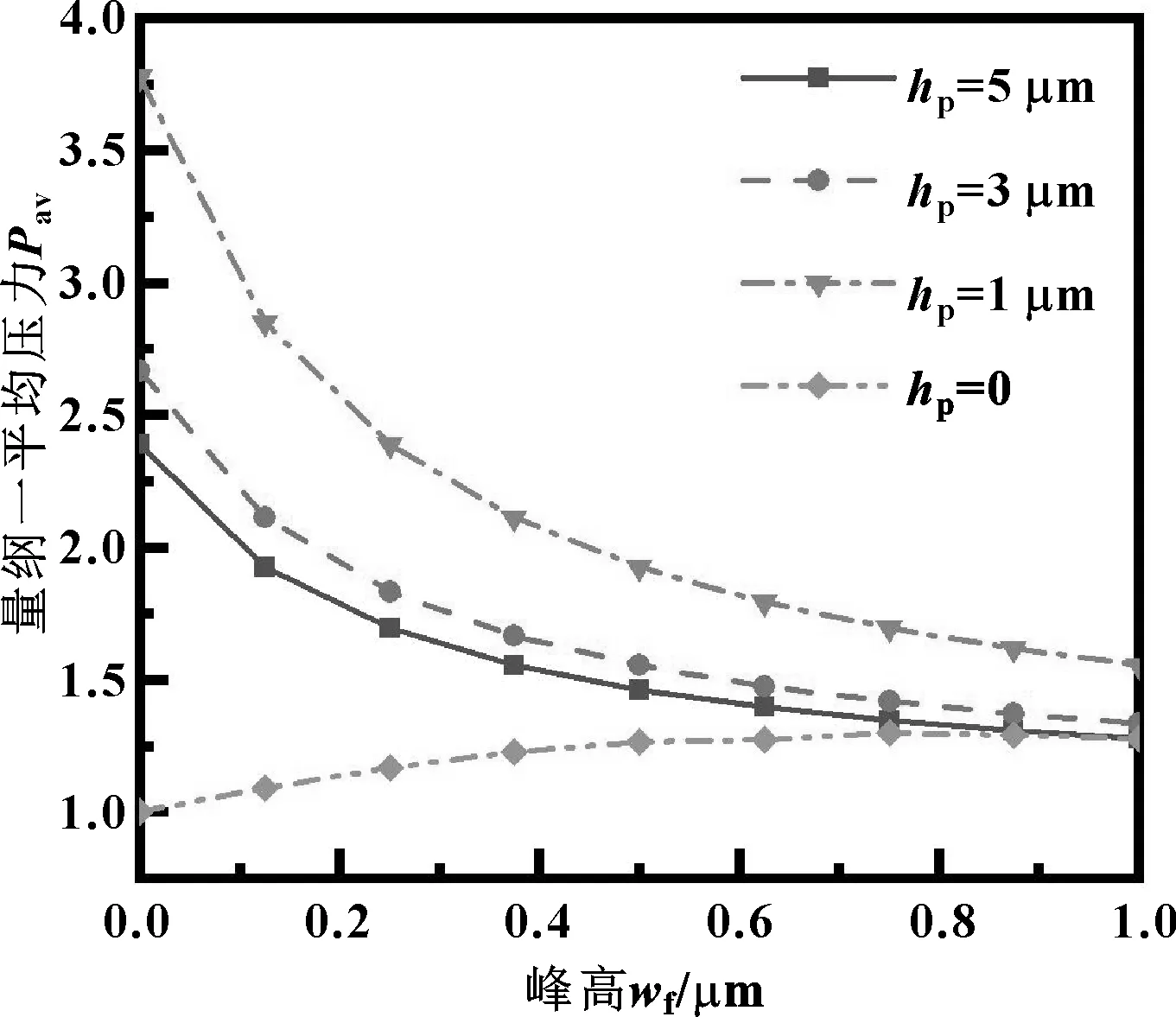
图11 粗糙峰峰高对量纲一平均压力的影响
由图11可知,当织构深度为0,即仅存在粗糙度的情况下,随着峰高的增大,平均量纲一压力呈现先增大后减小的趋势,且存在最佳峰高即0.7 μm,使平均压力达到最大;当织构深度大于0时,平均压力随峰高的增大而减小,原因是织构与粗糙度同时存在,平均压力受到这两方面因素的影响,织构产生的流体润滑效应受到粗糙峰的抑制,且峰高越大,抑制力越强,因此表面织构在实际的生产应用中,粗糙峰应尽可能地小。
4.3.2 粗糙峰波长对液膜压力的影响
图12示出了不同织构深度时,粗糙峰波长对平均压力的影响。
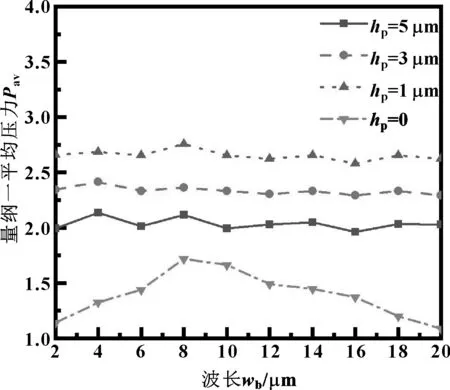
图12 粗糙峰波长对量纲一平均压力的影响
由图12可知,当织构深度为0,即仅存在粗糙度的情况下,随着波长的增大,平均量纲一压力先增大后减小,且存在最佳波长即8 μm,使平均压力达到最大;当织构深度大于0时,平均压力基本不随波长的增大而变化,与文献[12]中曲线趋势基本一致,原因是平均压力受粗糙度和织构两方面影响,当微凹坑织构的深度较大时,峰高相比于织构深度较小,对承载力的影响也较小。
5 结论
(1)圆台型织构的参数特征对以油、海水和水为介质的端面液膜压力有较大影响,相邻两织构的间距越大,液膜压力越小;圆台型织构大径越大,液膜压力越大,当大径近似等于小径时,即为圆柱型织构,此时的液膜压力最小;织构小径越大,液膜压力越小,当小径近似为0时,即为圆锥形织构,此时液膜压力最大;存在最佳织构深度使液膜压力最大。
(2)相同的情况下,密封端面油的平均膜压要高于海水的平均膜压,水的平均膜压相对最小,但油的黏度值过大会使摩擦力增大,温度升高,容易造成润滑膜破裂。因此选用合适的织构参数和润滑介质可以大大提高动静环接触端面的润滑性能。
(3)无织构情况下,存在最佳峰高和波长使端面平均膜压最大;存在圆台型织构的情况下,粗糙峰峰高越大,端面平均膜压越小,而粗糙峰波长对端面平均膜压的影响较小。因此,存在粗糙度参数与织构参数的最优组合使端面平均膜压达到最大值。
