弧面分度凸轮机构分度期润滑状态及油膜研究*

赵 帅 尹明富 朱 洋

(天津工业大学机械工程学院 天津 300387)

弧面分度凸轮机构是一种性能优越并且适用于高速分度的新型蜗杆式凸轮传动机构，又被称为福开森机构[1]。目前，国内外对弧面分度凸轮机构的研究发展很快，在空间啮合原理、运动和几何特性分析、动力学研究等方面都已经取得了一定的研究成果，为该机构的设计和生产提供了强大的理论基础[2]。随着国内机械制造业的飞快发展，空间凸轮机构成为不可或缺的核心传动件，但是缺少对弧面分度凸轮机构润滑性能的研究。

弧面分度凸轮机构能够按照特定规律进行周期性的分度和转位动作,在机构长时间的运动时，弧面分度凸轮工作轮廓曲面与转盘滚子曲面之间接触区域的位置在分度期时容易出现失效情况[3-4]，直接影响其传动效率、平稳性能以及使用寿命。因此，本文作者研究弧面分度凸轮机构分度期润滑状态及形成动态润滑油膜厚度。

1 弧面分度凸轮机构数学模型

1.1 弧面分度凸轮机构工作原理

常规的弧面分度凸轮机构由弧面分度凸轮和转盘组成。当弧面凸轮匀速转动，在其分度期会推动转盘转动，在其停歇期2个相邻的圆柱滚子会停留在凸轮凸脊的两侧。机构在分度期啮合的过程中，由于弧面凸轮与圆柱滚子2个线接触摩擦面的相对运动产生的动压效应，会形成弹流润滑油膜，进而达到保护机构的目的[5-6]。

1.2 建立机构的研究模型

在机构中建立的坐标系如图1所示：O0X0Y0Z0为与机架相连的定坐标系，O1X1Y1Z1为与弧面凸轮相连的动坐标系，O2X2Y2Z2为与转盘相连的动坐标系，O′0X′0Y′0Z′0为与机架相连的辅助定坐标系。

图1 机构中建立的笛卡尔坐标系

通过转盘圆柱滚子的曲面方程，选择一定的从动件的运动规律，以微分几何和旋转变量为基础，根据空间包络曲面的共轭原理，推导计算出弧面凸轮的工作廓面方程[7]。

表1为研究模型所采用的主要运动几何参数。

表1 主要运动几何参数

2 稳态工况下相关润滑参数求解

2.1 弹流润滑油膜厚度计算理论

弧面凸轮与圆柱滚子2个线接触摩擦面在进行相对运动时，会形成弹流润滑油膜。根据文献,可采用Hamrock-Dowson公式进行机构分度期啮合过程的最小油膜厚度Hmin的分析计算[8-9]。

(1)

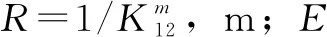
在稳态工况下，一般的传动机构所选用润滑油参数为η0=20×10-3Pa·s，α=2×10-8m2/N[10-11]。

根据公式分析，在机构保证润滑油参数一定的情况下，形成弹流油膜的厚度主要跟机构共轭接触处的卷吸速度、诱导主曲率、接触应力有关。

2.2 求解卷吸速度u

假设弧面凸轮与滚子之间的运动为纯滚动，弧面凸轮的速度为u1,圆柱滚子速度为u2，则

u1=ω1·rp1

(2)

u2=ω2·rp2

(3)

式中：ω1、ω2分别为弧面凸轮和圆柱滚子的角速度，rad/s；rp1、rp2分别为弧面凸轮和圆柱滚子的节圆半径，mm。

卷吸速度u为分度盘滚子接触点的绝对速度，表达式为

u=(u1+u2)/2

(4)

2.3 求解诱导主曲率

两曲面在接触点K处不发生根切的情况下，诱导法曲率在沿瞬时接触线方向为0，即诱导主曲率其中的一个解为0，对另一个诱导主曲率的求解过程如下：

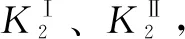
(5)

式中：β为圆柱滚子曲面坐标参数;φ为滚子的位置角。

(6)

(7)

其中

式中：ε2为转盘角加速度;ω1、ω2分别为弧面凸轮与滚子的角速度;c为机构的中心距。

根据欧拉公式可知，诱导主曲率方向为沿垂直于接触线切线方向，其值为

(8)

3 机构接触应力σ的算法推导

3.1 理论推导接触应力

弧面凸轮与圆柱滚子在分度期啮合时，2个曲面的接触形式为线接触，在接触面会有接触应力的产生。假设把弧面凸轮与从动滚子简化成圆柱体与平面相接触，以从动件圆柱滚子为研究对象，对机构分度期凸轮副的受力进行分析，在啮合过程中，凸轮副会产生法向压力Fn，Fn是影响接触应力大小的重要参数。

3.1.1 推导求解凸轮副法向压力Fn

以从动件为研究对象，在S2坐标系中，将法向力Fn分解为沿圆周方向的圆周力Ft，沿分度盘轴向的轴向力Fa和沿分度盘节圆半径的径向力Fr，如图2所示。

图2 受力分析

圆周力与法向力的夹角为β(β为圆柱滚子柱面坐标参数)，而从动件分度盘的节圆半径与法向力是垂直关系，所以Fr=0。因此

(9)

其中：

Fa=Fttanβ

(10)

利用机构的功能守恒原理对圆周力进行求解，将从动滚子简化成一个质点，稳态工况下，弧面凸轮近似做匀速转动，电机的输入功率全部转化为圆周力在分度期所做的功。当电机输入功率为P时，弧面分度凸轮机构在一个分度期内所消耗的功为w=Ptd，其中td机构的转位时间，可知：

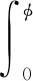
(11)

式中:φ为分度盘角位移;dφ为转盘角位移瞬时增量。

机构选定从动件的运动规律为修正正弦加速度运动，对式(11)进行变形求解得最大圆周力

(12)

式中：ω1为弧面凸轮转速;θh和φh分别为弧面凸轮和分度盘的分度角。

因此可以推导求得在一个分度期内啮合处所受圆周力的表达式为

(13)

将式(10)、(12)、(13)代入式(9)中即可得到凸轮副法向压力Fn。

3.1.2 求解凸轮副接触应力σ

在啮合过程中，主动件与从动件相接触的轮廓形状复杂，因此简化计算不会影响结果，初始接触长度B取滚子的高度。研究模型机构材料采用42CrMo，稳态工况下，弹性模量E1=E2=210 GPa，泊松比为μ1=μ2=0.3。根据弹性接触的Hertz理论对机构分度期凸轮副产生的接触应力进行求解[12]:

(14)

式中：Fn为凸轮副的法向压力。

将已知各参数代入(14)中，即可求凸轮副接触应力σ。

3.2 接触应力算法可行性仿真实验验证

利用ANSYS软件对建立的机构研究模型进行有限元分析，采用静力学分析模块对机构在分度期啮合过程中的接触应力进行求解，对主动件添加初始条件弧面分度凸轮转速为n=300 r/min，材料属性与理论推导条件相同，机构分度期接触应力分布结果如图3所示。

图3 弧面分度凸轮机构应力云图

利用MATLAB对接触应力算法进行仿真计算，与有限元分析保持相同的参数条件不变，表2为所得不同啮合位置接触应力四舍五入后的部分数据。

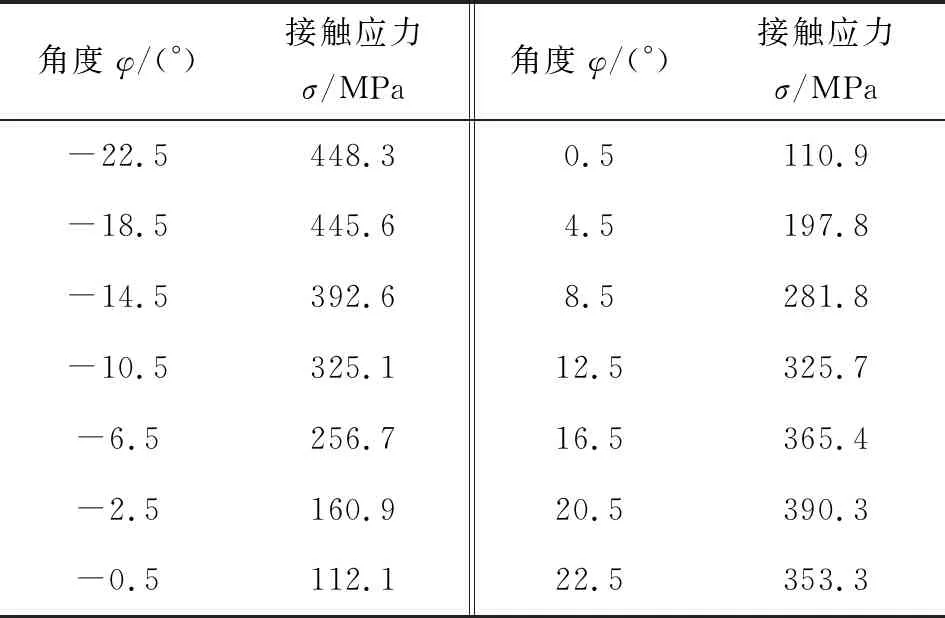
表2 不同啮合位置接触应力

2种不同仿真方法的数据结果相符合，在误差允许范围内，证明接触应力新算法推导可行。

4 实例仿真实验及润滑状态分析

弧面分度凸轮机构是一种中高速、承载能力强的传动机构。保证研究模型其他参数不变，改变主动件弧面分度凸轮的转速，研究不同转速条件下，机构的润滑状态及动态润滑油膜的形成。

4.1 不同转速对接触应力的影响

根据上文推导出的接触应力算法，利用MATLAB编写程序，对不同啮合点的接触应力进行仿真计算，主动件的转速n分别设定为300、600、900 r/min。仿真结果如图4所示。

图4 不同转速对接触应力的影响

凸轮转速越大，机构啮合处接触应力越小，凸轮转速的改变，不会改变接触应力变化的整体走向。

4.2 不同转速对形成弹流润滑油膜的影响

4.2.1 最小油膜厚度仿真

基于Hamrock-Dowson公式对不同啮合位置形成的最小油膜厚度进行仿真，主动件的转速n同样分别设定为300、600、900 r/min。不同转速的仿真结果如图5—7所示，X、Y分别代表凸轮工作廓面的位置坐标。

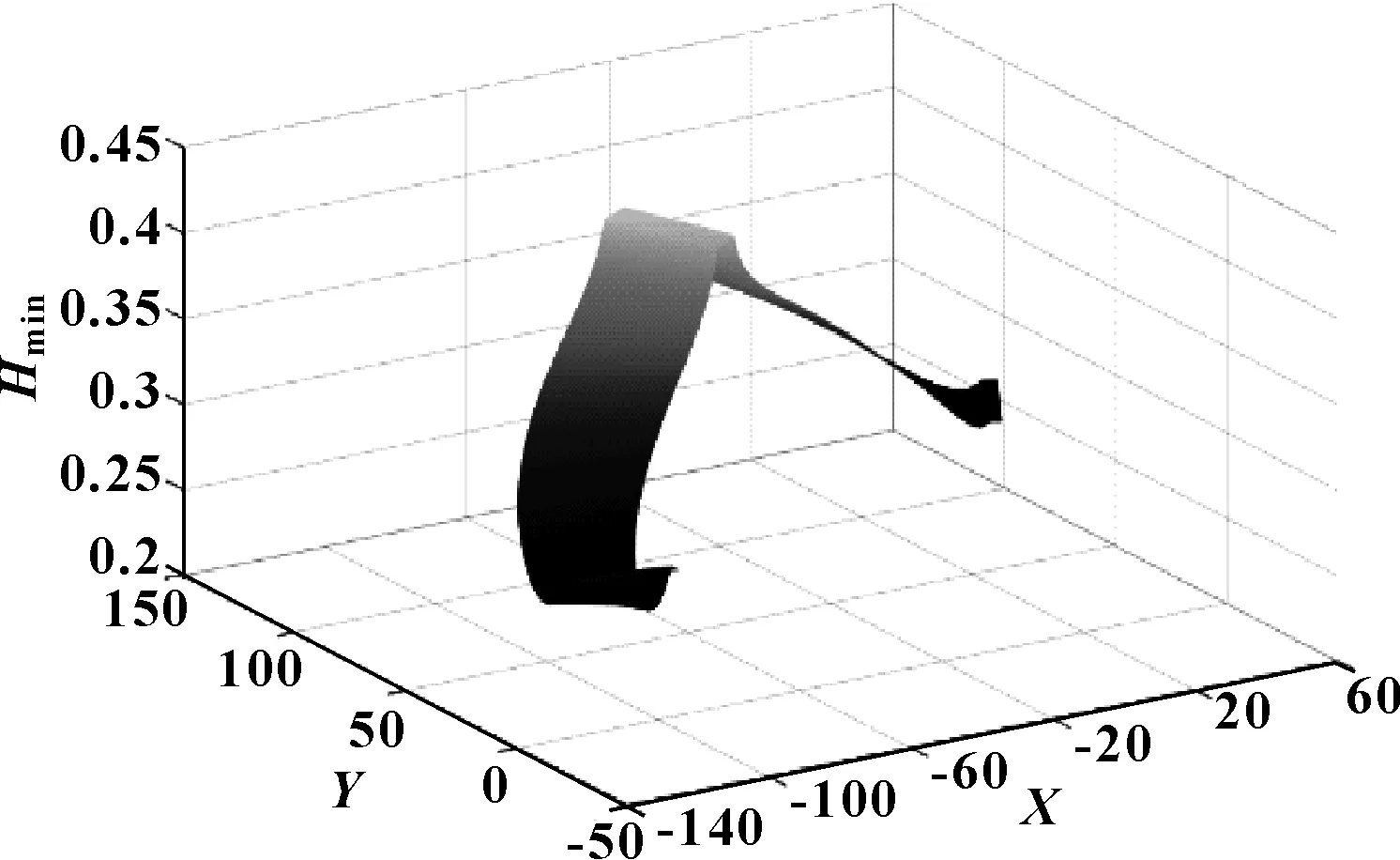
图5 300 r/min条件下的最小膜厚

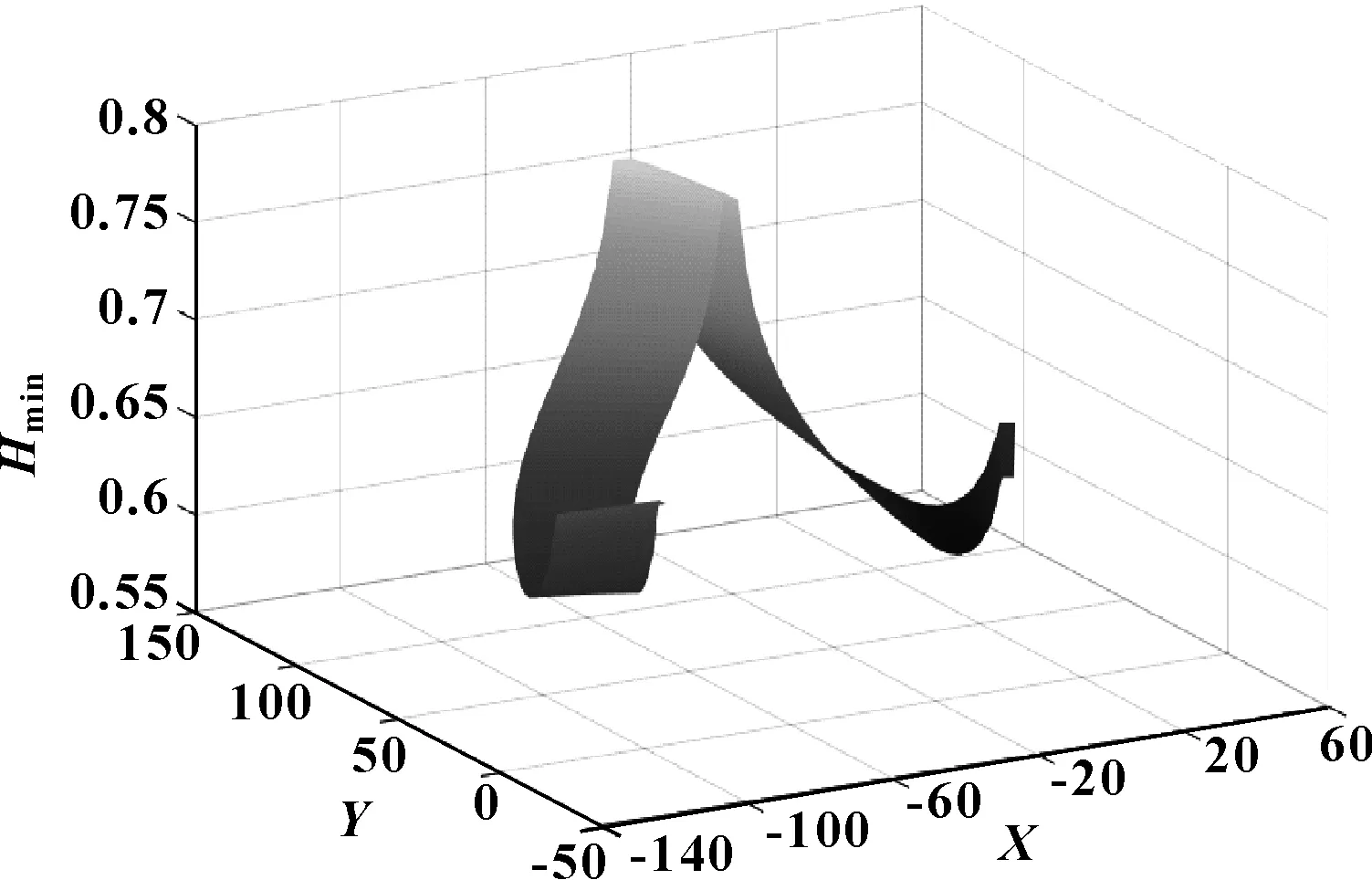
图7 900 r/min条件下的最小膜厚

从图中可以得出，凸轮转速越大，形成的最小油膜厚度越大。

4.2.2 膜厚比计算

为了更加准确地分析机构啮合过程的润滑状态，引用膜厚比概念对弹流润滑油膜进行分析。依据前人的实验数据总结[13-14]，如图8所示，当膜厚比λ<0.7(A区)，没有弹流润滑油膜产生，属于干摩擦状态，机构损伤严重。0.7≤λ≤1.5(B区)，属于混合润滑状态，成膜率小于50%，机构在传动过程中会产生滑动，降低机构寿命。1.5≤λ≤3(C区),成膜率大于50%，啮合过程工作表面的损伤会大大减小。λ≥3(D区)，属于流体润滑状态，不会发生摩擦，但是目前工业技术难以达到。

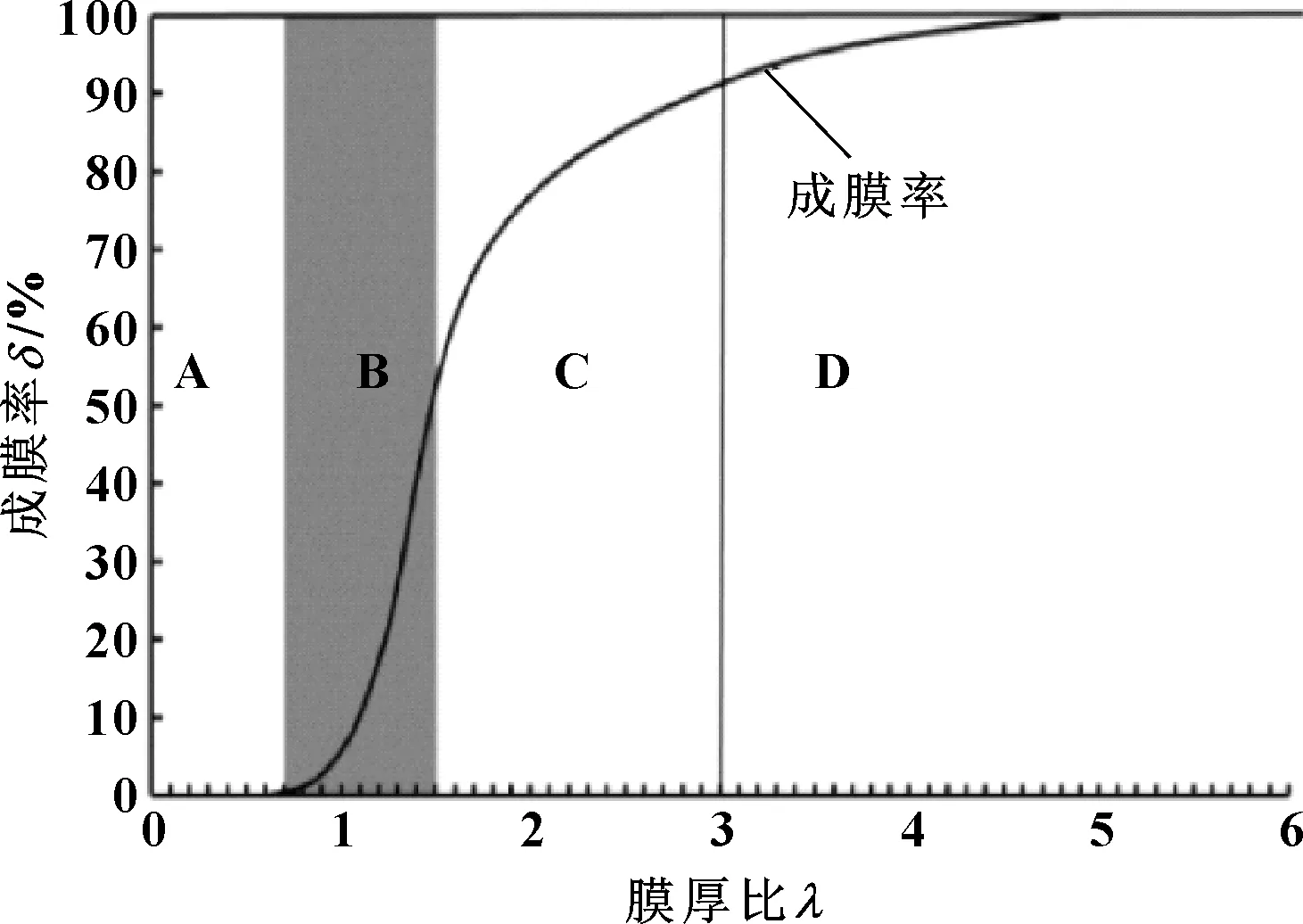
图8 成膜率与膜厚比关系

膜厚比计算公式为

(15)

式中：σ1、σ2分别为从动件和主动件表面粗糙度均方根偏差，分别取0.16、0.3 μm。

对不同转速下的膜厚比进行求解，结果如图9所示。

图9 不同转速条件的膜厚比

当机构低速传动时，分度期啮入段及啮出段膜厚比λ<0.1，成膜率极低，基本不能形成弹流润滑油膜，处于干摩擦状态，需要进行脂润滑。凸轮转速越大，越有利于形成弹流润滑油膜。

4.3 机构润滑状态仿真结果分析

从图4和图9得出的结果可知，接触应力和膜厚比的整体走向成反向。

分度期初期，机构啮合过程为单滚子啮合，期间接触应力较大，膜厚比较小，很难形成弹流润滑油膜。分度期达到中期，机构进行双滚子啮合，接触应力减小，形成的最小油膜厚度增加，成膜率也出现峰值。分度期末期，机构脱离双滚子啮合继续进行单滚子啮合，接触应力逐渐增大，形成的油膜厚度减小。

因此，在分度期初期以及分度期末期，也就是滚子刚进入啮合和即将离开啮合的区域，机构的润滑状态较差，最难形成润滑油膜，最易出现磨损失效。

5 结论

(1)针对弧面分度凸轮机构啮合特点，对分度期润滑状态进行分析，推导出两共轭曲面啮合过程受力的求解方法，并进行可行性验证。分析表明，在稳态工作情况下，卷吸速度、诱导主曲率以及接触应力是影响润滑油膜形成的关键因素。

(2)采用数值分析法对机构啮合分度期的最小油膜厚度进行求解。结果表明，在机构低转速的情况下，啮入段和啮出段极难形成弹流润滑油膜，为提高弧面分度凸轮机构的润滑性能提供理论依据。