无砟轨道箱梁系统振动试验相似模型的设计与校验
2021-07-22汪振国雷晓燕张新亚
罗 锟, 汪振国, 雷晓燕, 张新亚
(1.华东交通大学 铁路环境振动与噪声教育部工程研究中心,南昌 330013;2.大连理工大学 土木工程学院,辽宁 大连 116024)
桥梁结构模型试验是探索桥梁复杂内部规律与外部条件的重要方法之一。Guan等[1]为研究倒Y形主塔结构大跨度斜拉桥在强震荷载作用下的地震反映,按几何比尺35 ∶1设计制作了相似模型,模型中对斜拉索进行简化处理,结果表明简化后的模型误差保持在8%以下;Xu等[2]以几何比尺5 ∶1设计制作了钢箱梁、钢板梁和钢筋混凝土T型梁的相似模型,研究超高卡车与桥梁发生碰撞时,3种梁桥上部结构的动力性能变化;Murray等[3]设计建造了一个小比例尺预应力混凝土工字梁桥,通过开展剪切破坏模型试验,研究该桥的剪切特性。可以发现,桥梁模型试验多用来研究特殊工况条件下(如地震,破坏等)桥梁结构的动力与力学行为,而对于在正常服役状态下桥梁结构振动规律的研究却少有应用,特别是轨道交通中的桥梁结构,目前国内外还未有学者开展相关的模型试验,系统研究轨道交通桥梁结构振动与噪声辐射规律。
在高速铁路和城市轨道交通中桥梁占比很大,其在服役期间所产生的结构振动问题已受到广泛关注,相关研究表明[4-5]:长期处在桥梁结构振动所诱发的低频噪声环境中工作、生活,将会严重危害人的身心健康。此外,桥梁结构振动还会对沿线建筑物的安全以及沿线精密仪器的使用造成一定的影响[6-7]。针对该问题,目前的研究方法主要是数值模拟[8-9]和现场测试[10-11]。然而,单纯依靠数值模拟的方法是很难把握实际桥梁在服役过程中的各种影响因素;现场测试的开展又会受到场地、时限、人员安全等各种条件的制约;因此,以结构模型试验的方法来研究该问题是较为有效的手段之一。但是,如何保证桥梁原型与模型间准确的相似关系,确保模型上所呈现的现象与规律能正确的反演到原型桥上,是桥梁振动相似模型设计制作的难点所在,也是制约该方法在轨道交通桥梁结构振动噪声问题上得以广泛应用的原因。
林皋等[12-13]曾总结出结构动力模型试验有3种基本换算关系:弹性力相似律、重力相似律及弹性力—重力相似律。其中,以研究结构振动特性以及弹性阶段结构动力响应为试验目的时适用弹性力相似律。笔者曾利用该相似律指导制作了单箱梁的1/10缩尺模型,在验证相似理论与模型正确的基础上,开展了系列箱梁结构振动与噪声辐射的模型试验研究[14-16],研究表明:弹性力相似律适用于单体结构(单箱梁)振动相似模型的制作。但对于多层组合结构的振动相似模型,该相似律是否依然适用却未有文献报道。
为探究多层结构原型与模型间的相似关系,研究能准确反映多层结构原型振动规律的相似模型制作方法,本文首先从弹性力相似律理论出发,理清多层结构及其模型间的耦合相似关系;进一步以简单的双层结构为例,探讨结构层几何尺寸变化时对耦合相似关系的影响;之后以无砟轨道箱梁系统(4层结构)为原型,以10 ∶1为几何缩尺比,设计制作无砟轨道箱梁系统的相似模型;最后通过对模型进行自由模态测试以及有限元数值分析,对相似理论及模型进行校验。
1 弹性力相似律
1.1 单体(单层)结构弹性力相似律
弹性力相似律在模型设计中放弃了重力相似的要求,主要保持惯性力与弹性恢复力的相似。由相似理论可知:在动力过程中,无论由什么原因所产生的作用力,其比尺应保持一致。方程式表达为
F/Fm=λF
(1)
式中:F为原型的作用力;Fm为模型的作用力(下标“m”代表模型中的物理量,下同);λF为作用力比尺。
在动力作用过程中,对结构的动力性质产生影响的有重力、惯性力、弹性恢复力及其他外作用力,它们相应的作用力比尺如下。
重力
F/Fm=(ρ/ρm)·λ3
(2)
惯性力
(3)
弹性恢复力
F/Fm=(E/Em)·λ2
(4)
式中:ρ为材料密度;λ为几何比尺;λt为时间比尺;E为材料弹性模量。
依据弹性力相似律,要保持惯性力与弹性恢复力相似,据式(1)、式(3)、式(4)可推出
(5)
整理得
(5a)
由式(5a)可知,当以弹性力相似律指导相似模型设计时,材料的弹模比尺λE、密度比尺λρ和几何比尺λ是相互独立的,可供我们选择,在此基础上可导出时间比尺λt,进一步可导出其他动力特性相关的物理量比尺。例如
(6)
式中:u为位移;v为速度;a为加速度;f为频率;λu,λv,λa,λf分别为位移比尺、速度比尺、加速度比尺和频率比尺。
此外,线刚度比尺λK和面刚度比尺λKA可由作用力比尺λF与位移比尺λu表示,即
λK=(F/u)/(Fm/um)=λF/λu
(7)
(8)
式中,u为位移,其量纲与几何尺寸量纲相同,故其比尺λu与几何比尺λ相同。
由上述理论可知:对于单体(单层)结构,当以弹性力相似律指导相似模型设计时,可不用考虑模型材料问题,这使得相似模型制作更加便携,并降低试验成本。但对于多层结构,严格满足弹性力相似律将会导致各层结构间的材料属性相互关联。
1.2 多层结构弹性力相似律
图1为双层结构。结构原型第1层密度为ρ1,弹模为E1,几何尺寸为L1,第2层密度为ρ2,弹模为E2,几何尺寸为L2;结构模型第1层密度为ρ1m,弹模为E1m,几何尺寸为L1m,第2层密度为ρ2m,弹模为E2m,几何尺寸为L2m。由弹性力相似律可知,该结构具有两套相似关系。
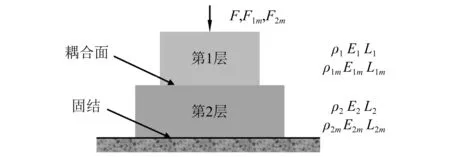
图1 双层结构
当结构原型施加外荷载F时,按第1层材料参数导出的外荷载相似关系可得作用于模型上的荷载为F1m,其关系式为
(9)
式中:λ1F,λ1t分别为按第1层材料参数导出的外荷载相似比与时间比尺;λ为几何比尺,双层结构中各结构层的几何比尺均相同。
按第2层材料参数导出的外荷载相似关系可得作用于模型上的荷载为F2m,其关系式为
(10)
式中,λ2F,λ2t分别为按第2层材料参数导出的外荷载相似比与时间比尺。
为严格满足弹性力相似律,则有:F1m=F2m,结合式(5a)、式(9)与式(10)可得
(11)
可以发现,当双层结构原型材料确定,即E1,E2已知,模型制作时只能自由选择其中一层结构的材料,另一层结构的材料参数则必须由前者导出。对于多层结构,要严格满足弹性力相似律,各层结构间的材料属性必然相互关联,这会极大增加多层结构相似模型的制作难度。
2 多层结构及其模型间的耦合相似关系
多层结构原型的振动方程为
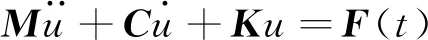
(12)
式中:M,C,K分别为结构的质量、阻尼及刚度矩阵;F(t)为外作用力;u为位移。
(13)
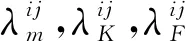
通过1.2节分析可知,若要严格满足弹性力相似律,多层结构的耦合质量、刚度与荷载比尺虽能求出,但实际模型制作时所需的材料却难以满足要求。从式(13)可以看出:多层结构耦合比尺λm,λK,λF不是按某一结构层材料属性所导出的相似比尺,而是由各结构层导出相似比尺耦合的结果,这就是多层结构中不同材料属性结构层间的耦合效应。倘若多层结构中某一层的几何尺寸远大于其他结构层,那么λm,λK,λF中大部分元素将由该结构层及其模型的材料属性决定,亦即λm,λK,λF近似等于该结构层的质量、刚度与荷载比尺,这样便可以忽略多层结构中不同材料属性结构层间的耦合效应,令相似模型近似满足弹性力相似律。
2.1 双层结构算例
以双层结构为例,如图2所示,原型结构尺寸为0.2 m×0.1 m×0.2 m(长×宽×高),分为上下两层,每一结构层几何尺寸相同,结构底面固结。按几何比尺λ=10构建双层结构的相似模型,原型与模型材料参数见表1,依据弹性力相似律,导出该结构的2套相似比尺如表2所示。
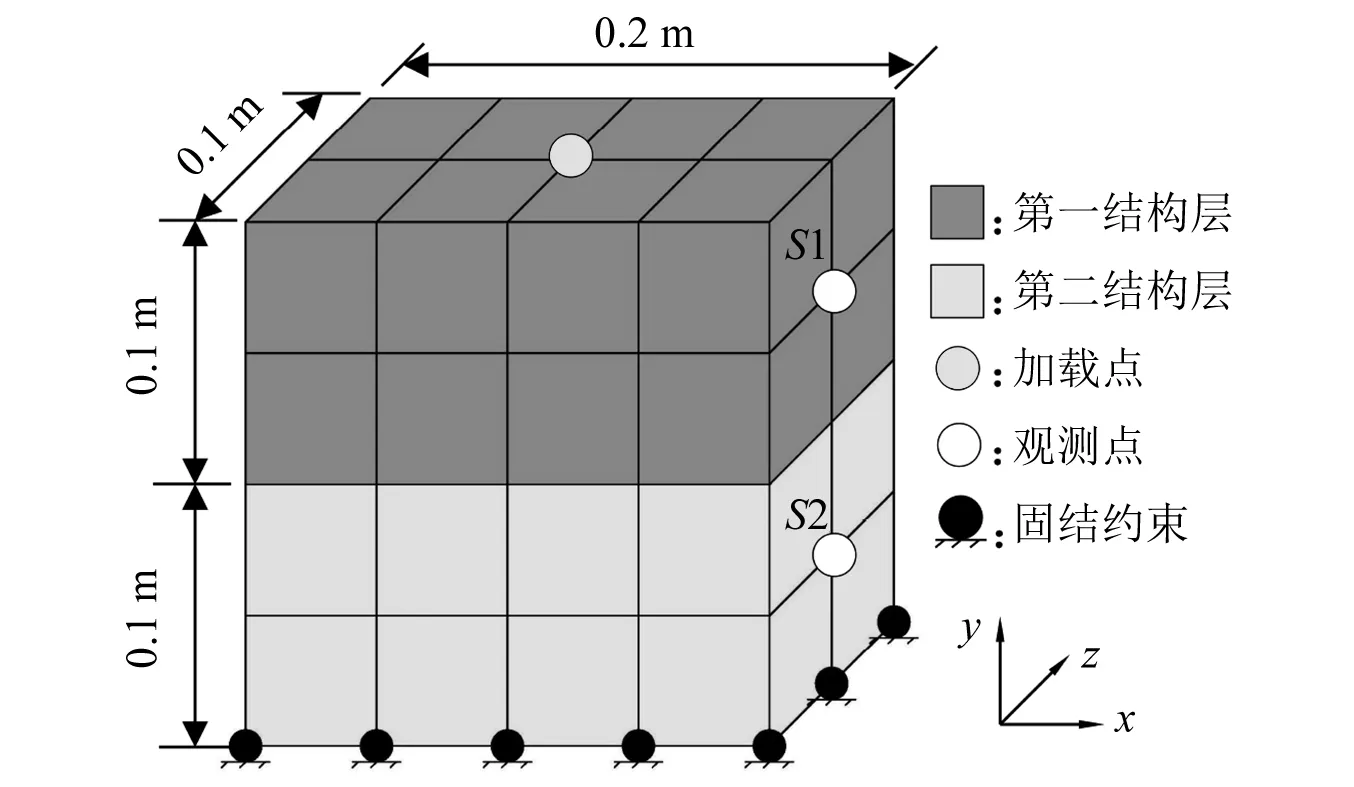
图2 双层结构原型
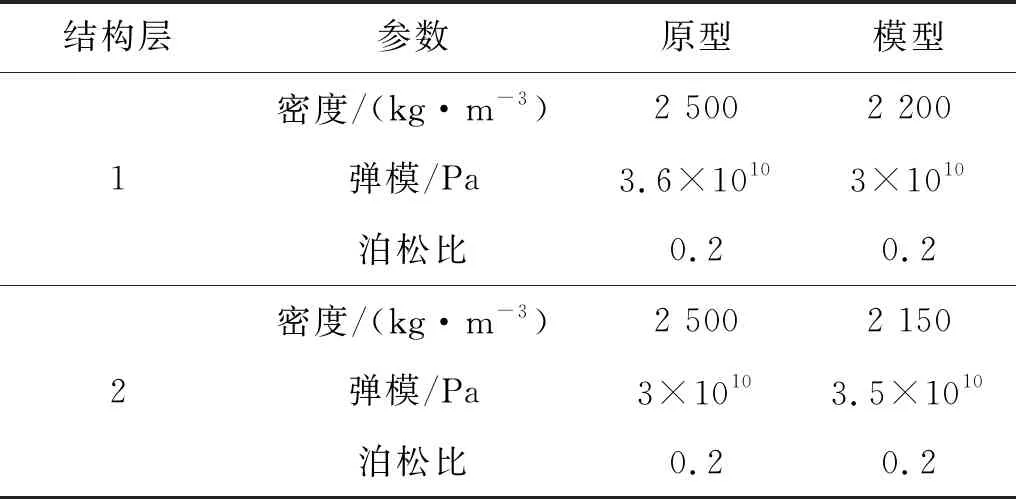
表1 原型与模型材料参数
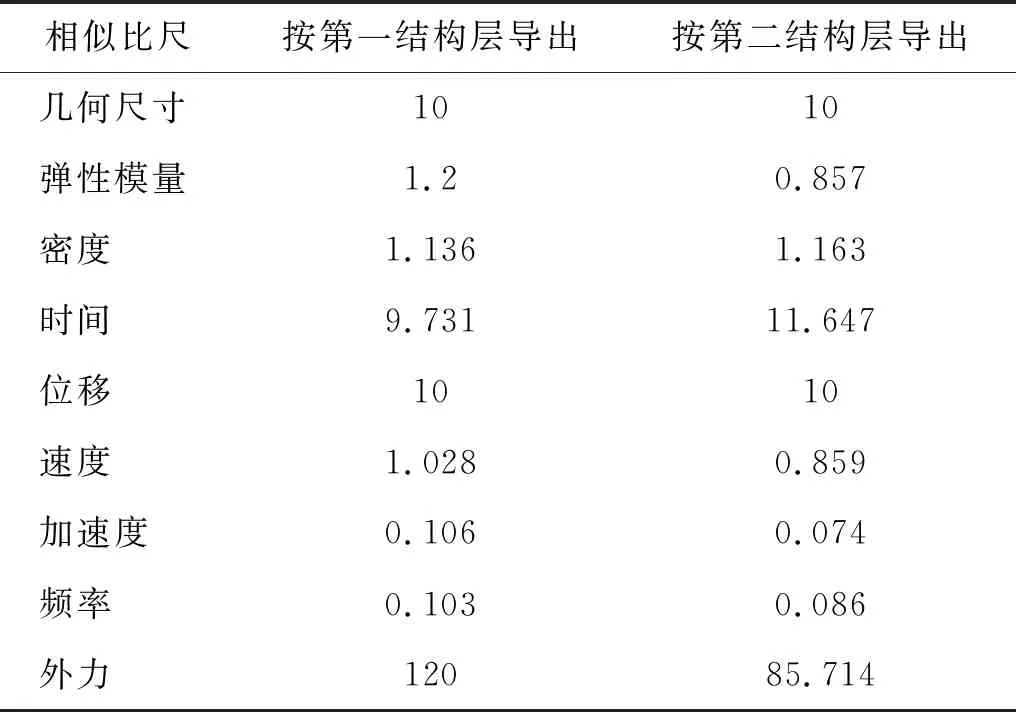
表2 双层结构相似比尺
对原型结构施加简谐荷载F,定义荷载幅值为500 N,频率为1 Hz,作用时间为5 s,步长为0.05 s。依据表2导出的相似关系,按第一结构层材料参数确定的模型上作用力F1m荷载幅值为4.167 N,频率为9.731 Hz,作用时间为0.513 8 s,步长为5.138×10-3s;按第二结构层材料参数确定的模型上作用力F2m荷载幅值为5.833 N,频率为11.647 Hz,作用时间为0.429 3 s,步长为4.293×10-3s。采用8节点正6面体单元划分结构,单元尺寸为0.05 m,采用竖向加载,加载点与观测点位置如图2所示。原型与模型结构外作用力为
(14)
简谐荷载作用下,双层结构观测点的竖向位移、速度和加速度时程如图3所示,图中:F为原型结构在外荷载F作用下观测点的时程曲线;F1m为模型结构在外荷载F1m作用下,观测点按第一结构层导出相似比反演后的时程曲线;F2m为模型结构在外荷载F2m作用下,观测点按第二结构层导出相似比反演后的时程曲线。
从图3可以看出:模型结构按两套相似比尺反演的S1点位移、速度、加速度幅值均与原型结构计算幅值相差很大,最小误差为14.5%;模型结构按第一结构层导出相似比反演,S2点的位移、速度、加速度幅值与原型结构计算幅值相差29%以上;模型结构按第二结构层导出相似比反演,S2点的位移、速度、加速度幅值与原型结构计算幅值相差较小,误差为1.3%。这表明该双层结构相似模型不能全面反映原型结构的振动规律,模型设计错误,弹性力相似律对于结构层几何尺寸相差不大的双层结构并不适用,模型反演结果与原型计算结果存在显著误差,这是由不同材料属性结构层间的耦合效应导致的。
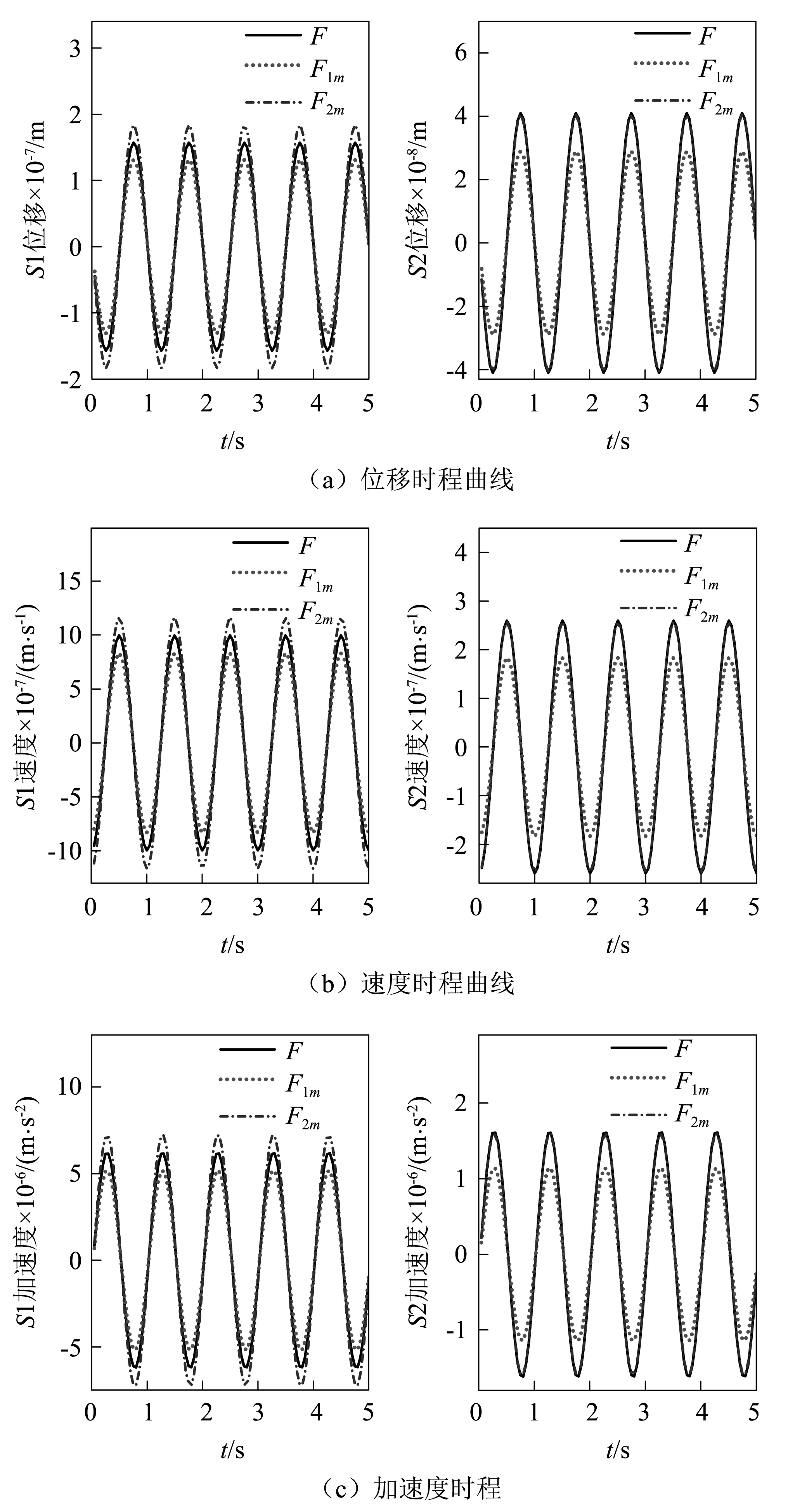
图3 计算结果
2.2 几何尺寸变化影响分析
以2.1节双层结构为初始模型,保持第一结构层几何尺寸不变,将第二结构层几何尺寸沿x,y向增大2倍、3倍和4倍,构成6种计算工况,如表3所示,外荷载大小及方向,加载点与观测点相对位置均与初始模型一致,以原型和模型反演观测点竖向位移、速度、加速度时程曲线幅值误差为指标,探讨双层结构几何尺寸变化对不同材料属性结构层间耦合效应的影响。
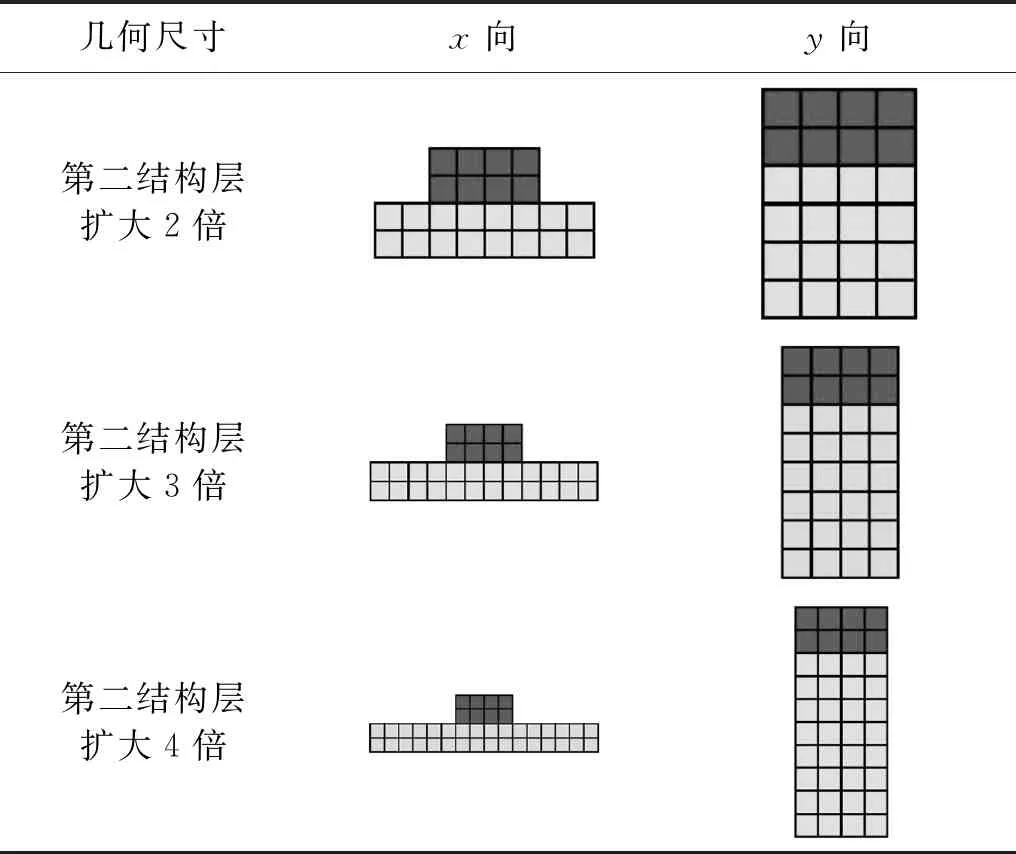
表3 计算工况
图4为第二结构层几何尺寸沿x向扩大时,模型反演结果与原型计算结果误差柱状图,图5为第二结构层沿y向扩大几何尺寸时的模型反演误差。图中:u,v,a分别为位移、速度、加速度;S1,S2为观测点位置;u-S1为模型S1观测点位移反演结果与原型位移计算结果间的误差,其余图例符号意义同上。
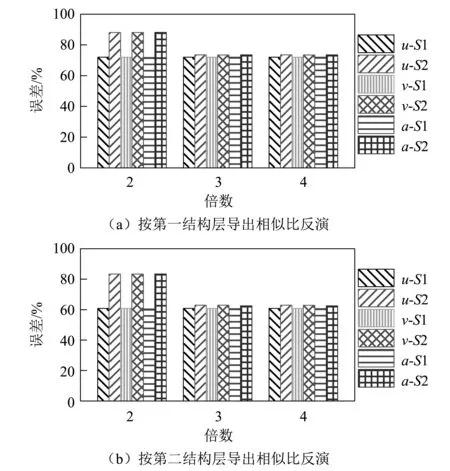
图4 沿x向扩大几何尺寸时模型反演误差
由图4可知:当第二结构层沿x向增大几何尺寸时,模型结构按两套相似比尺反演各观测点的速度、位移和加速度幅值,均与原型结构计算幅值存在显著误差,误差在60.413%~88.161%,且随着扩大倍数的增加,误差变化不大,这是因为荷载为y向,增大x向的几何尺寸对结构层间的耦合效应影响很小。
对比图4(a)与图5(a),发现模型结构按第一结构层导出相似关系反演各观测点的速度、位移和加速度幅值与原型结构计算幅值间的误差降低,且降幅明显,表明荷载方向与几何尺寸扩大方向一致时,能减小结构层间耦合效应。
从图5(a)可以看出:随着第二结构层y向几何尺寸的增大,模型反演与原型计算间的误差变化很小,表明当相似模型按某一结构层导出相似关系反演结果时,另一结构层的几何尺寸变化对结构层间耦合效应影响很小。
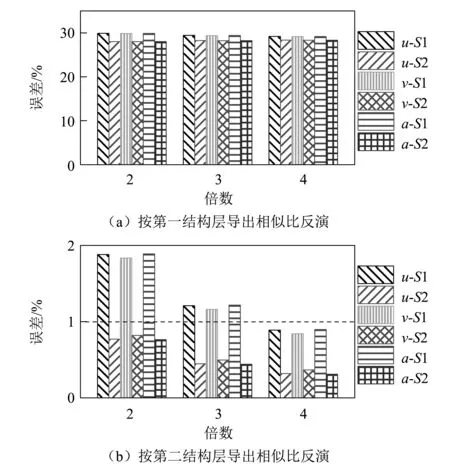
图5 沿y向扩大几何尺寸时模型反演误差
由图5(b)可知:当第二结构层沿y向增大几何尺寸时,模型结构按第二结构层导出相似关系反演各观测点的速度、位移和加速度幅值与原型结构计算幅值相差较小,误差在1.89%以下,且随着扩大倍数的增加,误差逐渐降低;当第二结构层几何尺寸沿y向扩大至4倍时,各观测点误差均小于1%,这表明此时相似模型已能较为精确地反映原型结构上的振动规律。从图5(b)还可看出:在不同扩大倍数工况下,观测点S1的误差均要大于观测点S2的误差,两者并不相等,说明此时原型与模型间的相似关系是近似于双层结构耦合相似关系的。
由此可见,当利用弹性力相似律指导制作多层结构的相似模型,且其某一结构层在荷载方向上的几何尺寸远大于其他结构层时,各结构层间的耦合效应微弱,且按该结构层所导出的相似关系将近似等于原型与模型间的耦合相似关系,制作的相似模型也可较为精确地反映原型结构的振动规律。
3 无砟轨道箱梁系统相似模型设计
以京沪高铁32 m简支箱梁桥为原型,如图6所示,该无砟轨道箱梁系统属于4层耦合结构,其不同材料属性层分别为:CHN60钢轨,CRTSII型轨道板,底座板和箱梁。轨道板与钢轨间通过扣件连接;底座板直接浇筑在箱梁之上,同时与轨道板间通过灌注CA砂浆连接;箱梁与下部结构通过支座进行连接。
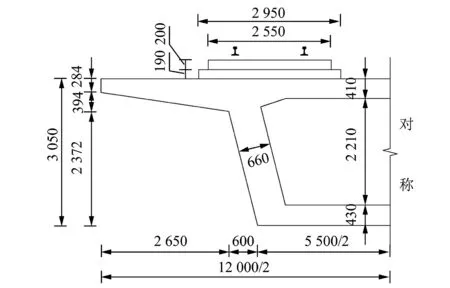
图6 无砟轨道箱梁系统跨中截面(mm)
轨道箱梁系统相似模型各结构几何尺寸均为原型的1/10,钢轨采用缩尺比为10 ∶1的定制钢轨,其材料参数由厂商提供;扣件采用螺栓紧固+弹性垫层模拟(见图7(a));轨道板、底座板和箱梁采用H60—Ⅲ型灌浆料进行分层浇筑,该型号灌浆料具有早强高强、自流动性好、无需振捣等特点,能较好地满足小尺寸模型桥梁的材料要求;CA砂浆层采用橡胶板模拟(见图7(b));采用钢板+弹性橡胶材料+钢板的形式模拟板式橡胶支座(见图7(c))。制作的轨道箱梁系统相似模型如图7(d)所示。轨道板、底座板及箱梁的密度、弹性模量通过试验浇筑过程中预留的试块进行测定,橡胶材料压缩刚度通过刚度测定装置试验确定。原型与模型的材料参数在表4列出。

图7 无砟轨道箱梁系统相似模型

表4 32 m简支箱梁桥原型与模型材料参数
列车过桥时,无砟轨道箱梁系统主要受竖向与横向荷载的作用,箱梁结构在这两个方向上的几何尺寸均要大于其他结构,因而轨道箱梁系统原型与模型间的相似关系可近似按箱梁结构材料参数导出,系统各物理量的相似比尺如表5所示。
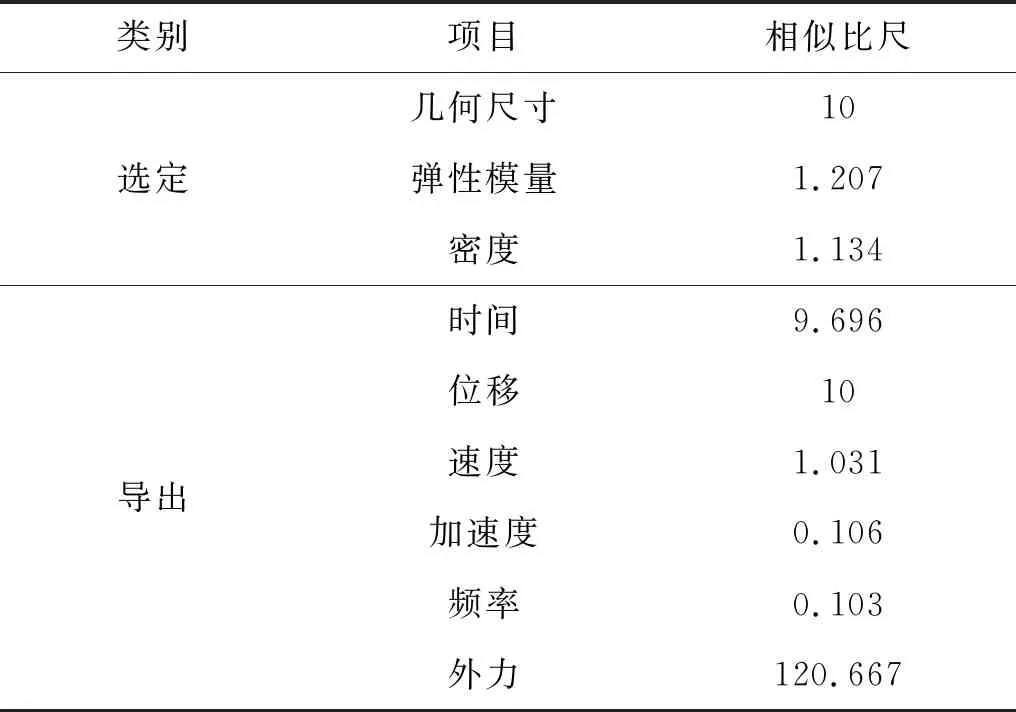
表5 无砟轨道箱梁系统相似关系
4 无砟轨道箱梁系统相似模型校验
4.1 自由模态测试
试验时将无砟轨道箱梁系统相似模型悬置(见图8(a)),在支座断面翼板处(见图8(b))布设一个激振点,同时沿桥长方向每隔0.4 m选取一个断面,共9个断面,每个断面布置22个拾振点(见图8(c)),全桥共计198个拾振点。拾振点上布设加速度传感器,激振点处布设力传感器,试验时采用LMS Test. Lab 软件的MIMO FRF Testing 模块测定相似模型的自由模态,该模块输出随机信号,经功率放大器放大后输出至激振器,激振器将随机信号以力的形式作用在模型上形成激励,此时数采设备通过传感器采集加速度与力信号,软件将两种信号处理成频响函数,通过对其进行分析处理便可获得相似模型的模态信息,测试方案如图8(d)所示。
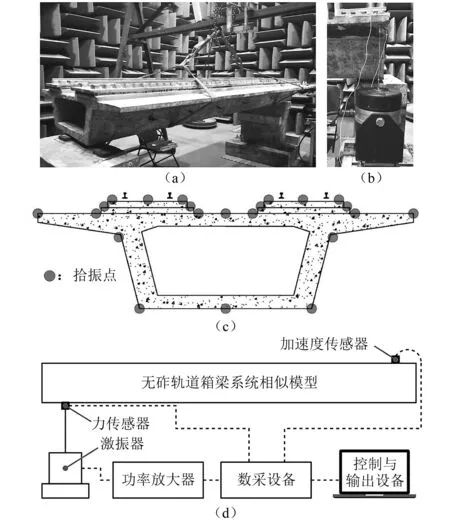
图8 自由模态测试
在0~250 Hz频率范围内共识别3阶模态,其模态置信度矩阵如表6所示。由表6可知:模态置信度矩阵非对角元均小于1%,对角元均为100%,表明所识别的各阶模态具有较好的独立性。
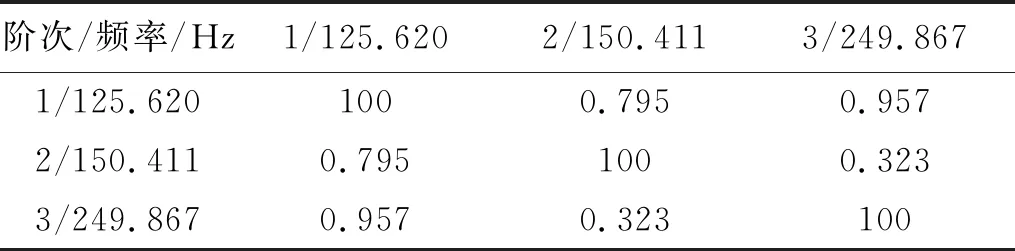
表6 模态置信度矩阵
利用ANSYS软件建立该相似模型的有限元模型。各结构层均采用实体单元模拟,材料参数见表4。对有限元模型进行模态分析,得到前三阶模态频率,将其与实测模态频率对比列于表7,模态振型对比如图9所示,其中左侧为有限元分析所得模态振型,右侧为实测模态振型。
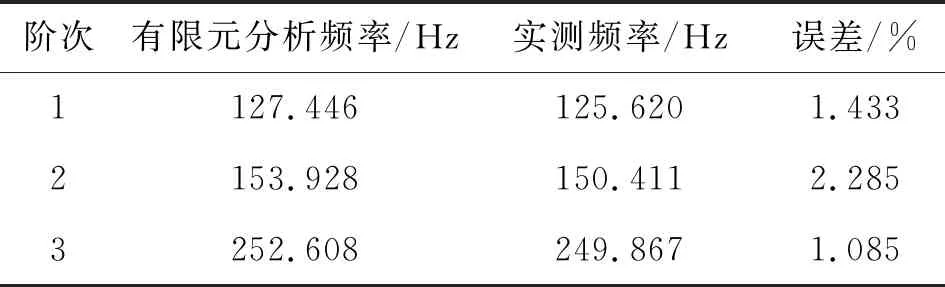
表7 自由模态频率对比

图9 自由模态振型对比
从表7和图9可以看出:前三阶自由模态实测结果与有限元分析结果吻合较好;实测结果与有限元分析结果具有较好的一致性,这表明相似模型制作正确,也说明ANSYS软件环境所建立的有限元模型较为可靠。
4.2 频率比尺校验
利用ANSYS软件建立无砟轨道箱梁系统原型和相似模型的有限元模型,材料参数见表4,对约束状态下的原型与模型进行模态分析,选取前5阶约束模态频率,考察两者间模态频率比尺与导出频率比尺是否一致,结果列于表8。由表8可知,有限元分析所得模态频率比尺与推导得出的频率比尺相差极小,表明频率比尺正确。
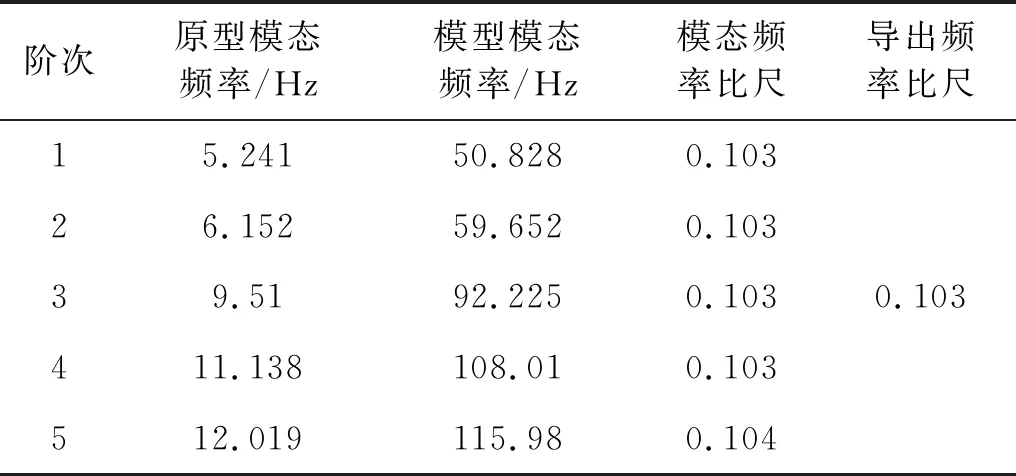
表8 模态频率比尺校验
4.3 动力参数比尺校验
分别建立无砟轨道箱梁系统原型和相似模型的有限元模型,并对其施加竖向简谐荷载,定义原型作用荷载F幅值为5 000 N,频率为1 Hz,作用时间为5 s,步长为0.05 s。依据表5导出的相似比尺,可得模型作用荷载Fm幅值为41.436 N,频率为9.696 Hz,作用时间为0.515 7 s,步长为5.157×10-3s。原型桥与模型桥外作用力为
(15)
在跨中截面选择轨顶处为加载点,并在每个部件上选择一个观测点,如图10所示。
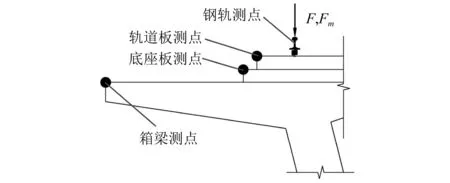
图10 加载点与观测点位置
将原型和模型(按表5相似比尺反演)各测点的位移u、速度v、加速度a幅值频谱曲线进行对比分析,以此校验各动力参数比尺的正确性,如图11所示。图中:F为原型测点幅值谱;Fm为模型测点按相似关系反演后的幅值谱;w为峰值误差。
从图11可以看出:原型轨道箱梁系统各测点处位移、速度、加速度幅值谱,与模型按相似关系反演后相应的幅值谱近乎重合,仅峰值大小稍有差别;各测点处峰值频率均为1 Hz,这是由原型简谐荷载的频率决定的;钢轨测点处原型与模型反演后的位移、速度、加速度峰值相差较大,误差分别为:3.652%,3.682%,4.02%,而其余测点处两者误差极小,均在0.5%左右,这可能是因为钢轨与轨道板间存在特殊的连接方式(0.65 m固定间距的扣件),使得相似模型中钢轨与其他结构层间的关联性降低,所以当按箱梁材料属性导出的相似关系反演钢轨的振动响应时,结果误差会增大,但从本例来看,该误差是可接受的。
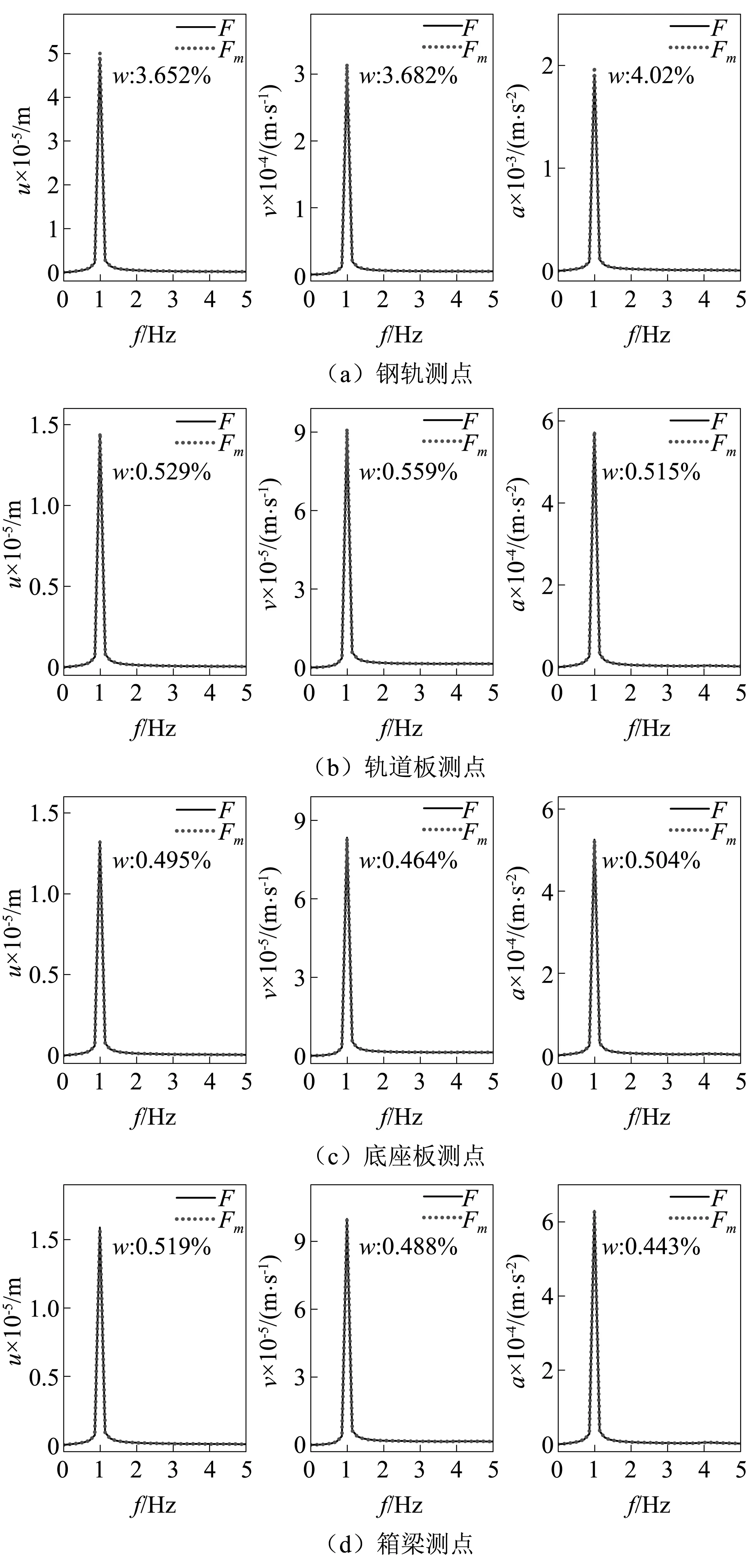
图11 原型与模型反演后各测点幅值谱对比
由此可见,针对无砟轨道箱梁系统,可依据弹性力相似律设计其振动试验相似模型,相似关系只需按箱梁材料属性导出,且模型中其他结构所用材料可根据需要合理选择,这将极大方便模型制作,同时降低试验成本。
5 结 论
(1) 对于各结构层沿荷载方向上几何尺寸相当的多层结构,由于不同材料属性结构层间存在耦合效应,弹性力相似律将不适用于多层结构振动相似模型的设计。
(2) 当利用弹性力相似律指导制作多层结构振动试验的相似模型,且其某一结构层在荷载方向上的几何尺寸远大于其他结构层时,按该结构层材料属性导出的相似关系将近似等于原型与模型间的耦合相似关系,制作的相似模型也可较为精确地反映原型结构的振动规律。
(3) 针对无砟轨道箱梁系统,可依据弹性力相似律设计其振动试验相似模型,相似关系只需按箱梁材料属性导出,且模型中其他结构所用材料可按需要合理选择。
