防屈曲支撑在结构设计中的若干参数匹配问题讨论
2021-07-22吴克川余文正张龙飞
吴克川, 陶 忠, 余文正, 兰 香, 张龙飞
(1. 昆明学院 建筑工程学院,昆明 650214; 2. 昆明理工大学 土木工程系,昆明 650500)
防屈曲支撑[1](buckling-restrained brace,BRB)是一种通过限制失稳获得较高受压承载力的耗能减震构件,主要由核心耗能部件与外围约束部件组成,其中,核心耗能部件由耗能段、过渡段及弹性连接段串联而成。对于不同的抗震性能需求及工程应用模式,BRB既可发挥普通支撑的功能(增加结构抗侧刚度),也可起到消能器的作用(屈服耗能增加结构阻尼),目前BRB在日本、美国、意大利等地震多发国家得到广泛应用[2-3]。随着抗震技术的发展和提高,我国自主设计生产的各类BRB在工程中的应用日益增多,相关技术规范也逐渐得到完善。从工程应用的角度来看,BRB主要分为承载型、耗能型及阻尼型三种[4](分别记为第Ⅰ类、第Ⅱ类及第Ⅲ类BRB),承载型BRB在各水准地震作用下均保持弹性,仅提供附加刚度;耗能型BRB在多遇地震作用下保持弹性,在设防地震作用和罕遇地震作用下屈服耗能;阻尼型BRB则在多遇地震作用下即屈服作为阻尼器使用。对于承载型BRB结构的设计,仅需考虑刚度需求,设计人员往往较易把握,然而,对于耗能型及阻尼型BRB结构的设计,涉及到BRB产品自身技术参数(屈服承载力、屈服位移,轴向刚度、芯材屈服强度等)及其与结构参数(屈服位移、弹性刚度等)的匹配问题,设计人员由于对设计方法的不熟悉,可能给出不合理的BRB技术参数,导致难以实现结构的抗震性能目标,或无法顺利完成产品设计,同时这些技术参数还受到BRB结构等效模型参数的影响,使其合理的设计取值更为复杂。
目前,关于BRB在结构设计中参数合理控制的研究较少[5],基于此,本文对不同类型BRB的性能参数与结构间参数的关系进行理论推导,建立BRB各参数间以及各参数与结构参数间的关系式,分析影响BRB与结构间参数匹配的影响因素,并给出相应的参数控制建议,采用算例分析验证所提出参数控制建议的有效性,以供工程设计参考。
1 BRB产品技术参数的合理匹配
在进行防屈曲支撑减震结构设计时,通常涉及到的BRB产品技术参数有5个,包括屈服承载力、屈服位移、轴向刚度、第二刚度系数、支撑长度,设计人员在结构设计中应用BRB时须明确给上述5个参数,以提供给产品工程师完成产品设计。由于目前国内的主流结构设计软件PKPM及YJK等无法精确模拟包含连接节点板在内的BRB的完整力学行为,因此设计人员通常在结构模型中采用一等代钢支撑来等效模拟BRB,见图1,并且可根据确定的结构方案及结构刚度需求明确给出支撑长度及轴向刚度两个参数,同时根据等代钢支撑的应力水平给出截面面积,但该长度为BRB两端工作点间的长度(与BRB相连接梁、柱交点间距离),轴向刚度为包含节点板在内的等效轴向刚度,截面面积为等代钢支撑的等效截面面积,并非BRB产品自身实际的长度、轴向刚度及截面面积,如果给出的以上3个参数不相匹配,则可能无法完成产品设计。然而,设计人员对上述参数间的合理匹配及BRB等效参数与实际参数间的关系不甚了解,往往难以判断所给出的参数是否合理。
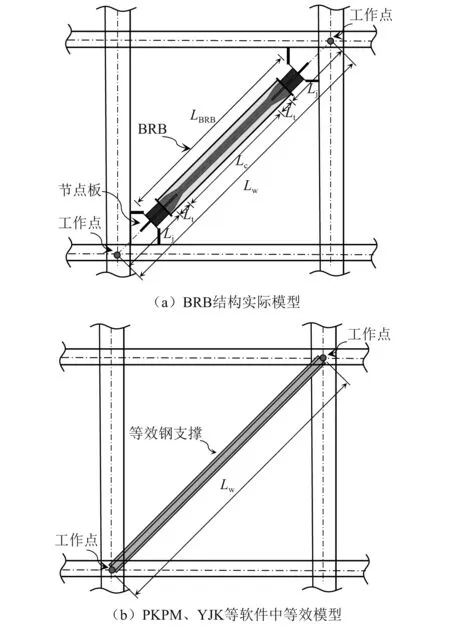
注:Lw为BRB工作点间长度; Lc,Lt,Lj分别为BRB耗能段、过渡段、连接段长度; LBRB为BRB实际长度。
1.1 BRB实际参数与等效参数间关系
防屈曲支撑的等效轴向刚度Keff与其各串联部分的组成有关,见图2,设计人员容易明确给出的等效参数为等代钢支撑的刚度Keff、工作点间的长度Lw及截面面积Ae,但BRB的芯材截面面积Ac及材料强度fy等实际参数如何合理取值不被设计人员所熟知。
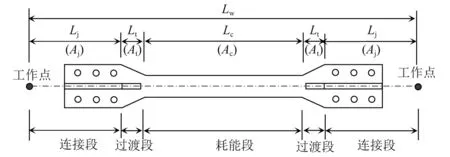
图2 BRB轴向串联组成
根据图2中BRB轴向串联组成,BRB连接段、过渡段、耗能段的长度及截面面积有如下关系[6]
Lc=ξcLw, 2Lt=ξtLw, 2Lj=ξjLw
(1)
At=βtAc,Aj=βjAc
(2)
式中:ξc+ξt+ξj=1;βt,βj分别为过渡段截面面积At、连接段截面面积Aj与耗能段截面面积Ac之比。
BRB的等效轴向刚度由连接段、过渡段、耗能段三部分串联而成,则按刚度串联原则有
(3)
将式(1)式(2)代入式(3)得
(4)
式中,E为芯材弹性模量。
在进行结构设计时,BRB的等效轴向刚度应与等代钢支撑的轴向刚度保持一致,即
(5)
将文献[7]中的等效刚度系数扩展应用到描述BRB实际参数与等效参数关系,即定义参数匹配系数Qm,进一步将式(5)改写为
(6)
式(5)及式(6)即为防屈曲支撑等效参数与实际参数间的关系式,不难看出,两参数间的变化关系与匹配系数Qm的取值有关,即两参数间的匹配程度受到BRB各组成部分的长度及截面面积的影响,如果Qm的取值不合理,则可能无法完成产品设计,相应可通过合理控制Qm的取值避免这一问题。
在BRB的轴向组成中,过渡段的作用是使轴力平缓传递,避免出现应力集中,其长度变化范围较小,约为BRB总长度的5%,截面面积约为耗能段截面面积的1.5~2.0倍[8]。图3为式(6)中βt取2、ξt取0.05时,匹配系数Qm在不同βj取值下随变量ξc的变化曲线,从图中可以看出:①BRB芯材截面积的取值主要受耗能段长度及连接段截面积影响;②耗能段长度相同时,连接段截面积越大,耗能段截面积取值越小;③连接段截面积相同时,耗能段长度越长,其截面积取值越大;④连接段截面积越大,耗能段长度对BRB芯材截面积取值的影响越显著。
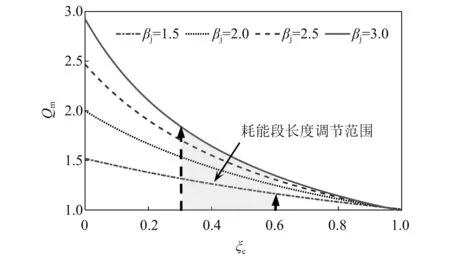
图3 匹配系数Qm变化曲线
当匹配系数Qm取值过小时,可能出现BRB耗能段长度及截面面积过大的情况,以致阻尼型及耗能型BRB无法实现屈服耗能的目标;Qm取值过大时,则可能出现BRB耗能段长度及截面面积过小的情况,以致承载型及耗能型BRB无法实现多遇地震作用下保持弹性工作的目标,甚至无法保证在罕遇地震作用下的变形需求而被拉断。因此,对于不同类型的BRB应合理控制系数Qm的取值,使其实现不同水准地震作用下的性能目标。目前,工程中应用的BRB芯材材料有BLY100、BLY160、BLY225、Q235、Q345、Q390等,根据以上材料强度范围,通过调整耗能段长度及截面积大小可实现各类BRB的工作性能目标,当ξc取值为0.3~0.6时[9],可在实现上述BRB性能目标的基础上完成产品设计,相应的Qm=1.1~1.8,即Ac=(0.55~0.90)Ae,设计人员在进行BRB结构设计时,可通过具体的Qm取值确定合理的BRB芯材截面面积。
1.2 BRB屈服荷载Fy与等效刚度Keff的合理匹配
设计人员在确定等代钢支撑参数的过程中,需要合理控制的另一个参数为钢支撑在多遇地震作用下的应力比κ(支撑实际受力与屈服承载力之比),即当等代钢支撑的材料强度fye及长度Lw确定的情况下,应当合理的确定等效截面积Ae,此时钢支撑的等效轴向荷载为
Fe=κfyeAe
(7)
BRB可根据等代钢支撑不同的应力水平选择材料强度fy,以使其屈服荷载与等效轴向荷载匹配,其实际屈服荷载为
Fy=fyAc
(8)
对于各类型BRB在多遇地震作用下保持弹性或塑性工作状态的临界条件为式(7)与式(8)相等,即
fyAc=κfyeAe
(9)
式(9)可进一步改写为等效轴向刚度与屈服荷载的关系式
(10)
由1.1节分析可知,Qm取值范围为1.1~1.8,fy/fye的取值范围为0.43~1.66(设计人员通常选用的等代钢支撑材料强度为235 MPa,BRB芯材材料强度范围为100~390 MPa)。图4为应力比κ对应BRB不同工作状态时的取值与匹配系数Qm的关系,从图中可以看出,等代钢支撑应力水平的大小影响着BRB在多遇地震作用下的工作状态,κ值不能过大也不能过小,应合理控制其取值范围,当根据刚度需求确定等代钢支撑轴向刚度后,如果应力比κ的取值落在图中虚线与点划线之间,则可通过选用低屈服点钢材或减小耗能段长度的办法实现在较小屈服荷载下获得较大的支撑轴向刚度,并可使BRB保持弹性工作状态;如果应力比κ的取值落在图中虚线与点线之间,则可通过选用高强钢或增加耗能段长度的办法实现在较大屈服荷载下获得较小的支撑轴向刚度,并可使BRB屈服耗能;如果应力比κ的取值落在图中阴影区域以下或以上,则超过低屈服点钢材或高强钢材的选择范围,且无法通过合适的Qm取值进行调整。因此在结构设计中确定等代钢支撑轴向刚度时,应使支撑应力比κ的取值落在图中阴影区域内,不同类型BRB对应等代钢支撑应力比κ的建议取值范围见表1。
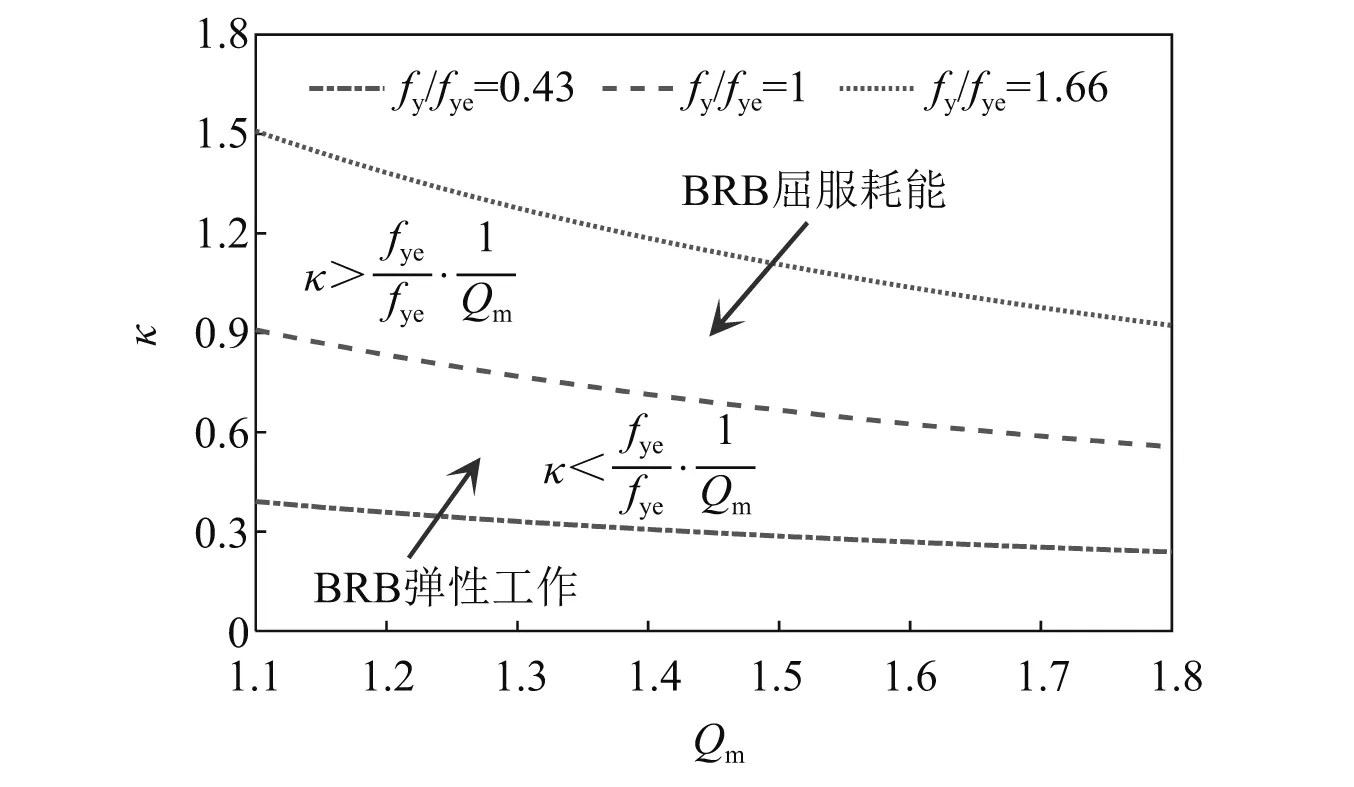
图4 应力比κ合理取值范围
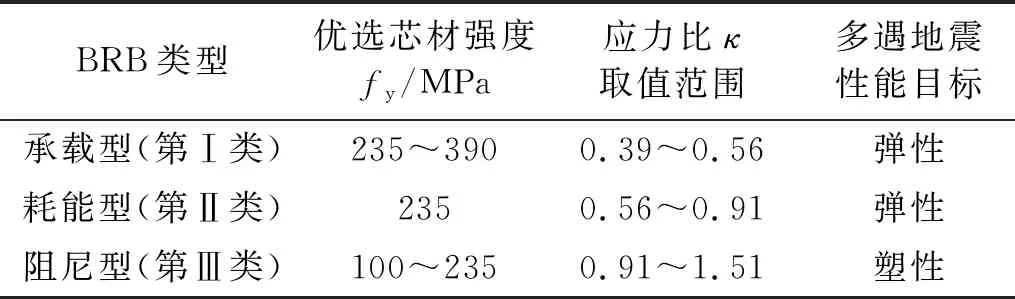
表1 各类BRB等代钢支撑应力比合理取值
1.3 BRB屈服位移δy与支撑长度Lw的合理匹配
防屈曲支撑在轴向由各组成部分串联而成,屈服位移也与各部分的组成相关,屈服位移δy与其长度Lw的关系为
(11)
由式(11)可知,在支撑长度Lw确定的情况下,屈服位移的大小主要取决于材料强度fy及匹配系数Qm的取值,即材料强度fy与耗能段长度Lc的影响,想要提高屈服位移,可通过选用高强钢或增加耗能段长度实现,反之可选用低屈服点刚或减小耗能段长度。图5为根据式(11)绘制的BRB屈服应变εy在保证可完成产品设计的基础上合理的取值范围,从图中可以看出,匹配系数Qm对屈服应变的影响程度随材料强度的增加而提高,采用低屈服点钢材时,在BRB产品设计过程中耗能段的长度有更广的调节范围。
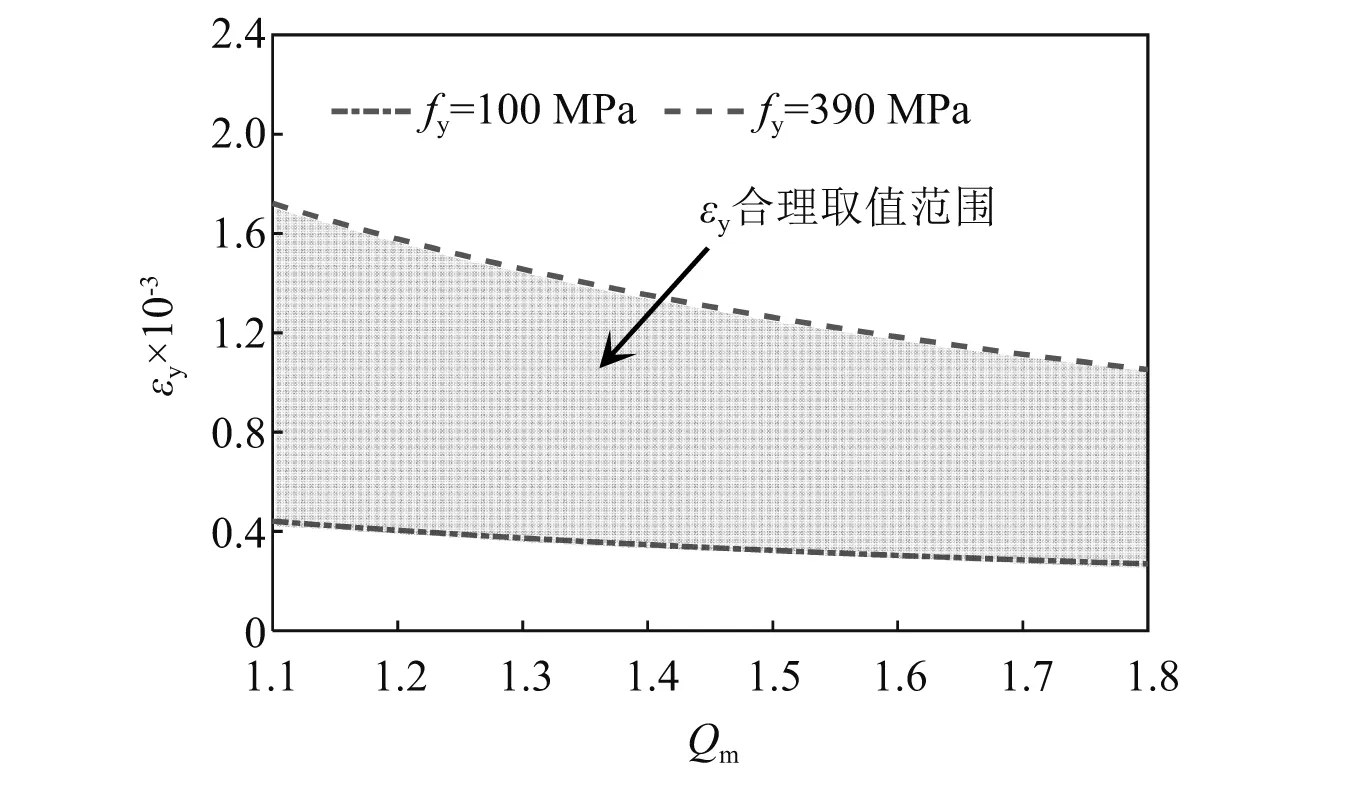
图5 屈服应变εy合理取值范围
2 BRB参数与结构参数的合理匹配
地震作用下,结构中的防屈曲支撑作为耗能减震构件,起到结构第一道抗震防线的作用,应先于主体框架进入屈服耗能状态,BRB与主体结构间的先后屈服顺序与其自身的产品技术参数及结构的性能参数有关,二者的匹配关系将影响设计结果的合理性,同样,BRB在何水准地震作用下进入屈服耗能状态,并且在罕遇地震作用下保持正常工作而不断裂破坏的条件与上述参数间的合理匹配相关。本文以BRB在结构中的布置形式为单斜撑布置为例建立BRB参数与主体结构参数间的关系,并分析参数间的合理匹配关系,其结论同样适用于BRB为“人字型”或“V字型”布置的结构。
2.1 BRB耗能段应变εc与结构层间侧移θ关系
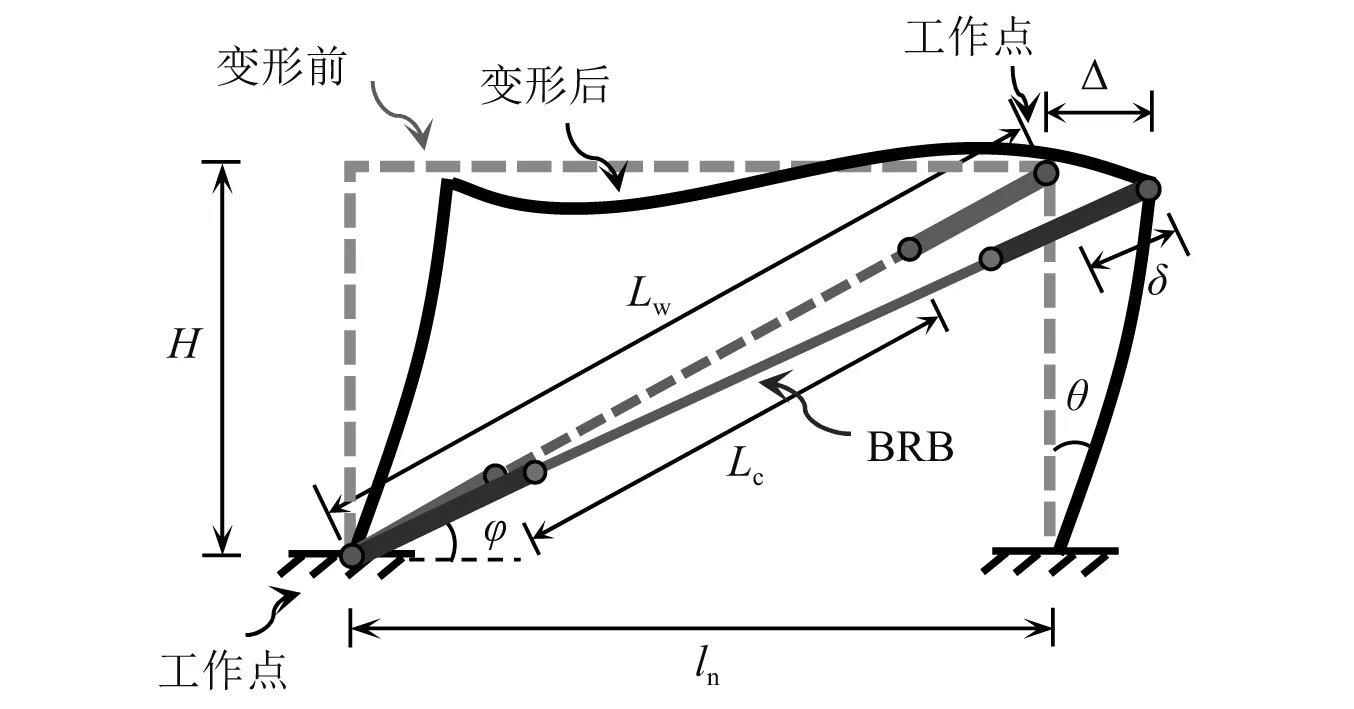
图6 BRB结构变形计算简图
BRB的轴向平均变形δa为耗能段变形δc、过渡段变形δt及连接段变形δj之和,即
δa=δc+δt+δj
(12)
进一步将式(12)改写为应变的表达方式
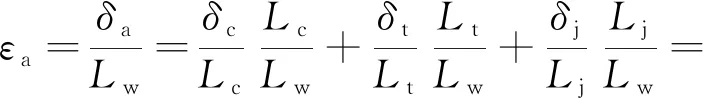
(13)
式中,εa,εc,εt,εj分别为BRB轴向平均应变、耗能段应变、过渡段应变、连接段应变。
由于BRB连接段及过渡段在各水准地震作用下均保持弹性,即该部位的最大应变小于材料的屈服应变,尤其在大变形情况下,已有的研究表明[11],该应变占BRB轴向平均总应变的比例小于6%,因此略去该部分变形对轴向应变的贡献,即
(14)
图7为BRB布置角度为45°,耗能段长度不同取值下,BRB耗能段应变随结构层间位移角的变化曲线。从图中可以看出,耗能段长度占BRB总长度一半时(ξc=0.5),其应变值与层间位移角呈正相关变化关系;当结构层间变形确定时,耗能段应变随ξc的增加而减小;在结构产生大变形时(例如θ=3%),ξc的取值对耗能段应变的影响更为显著。
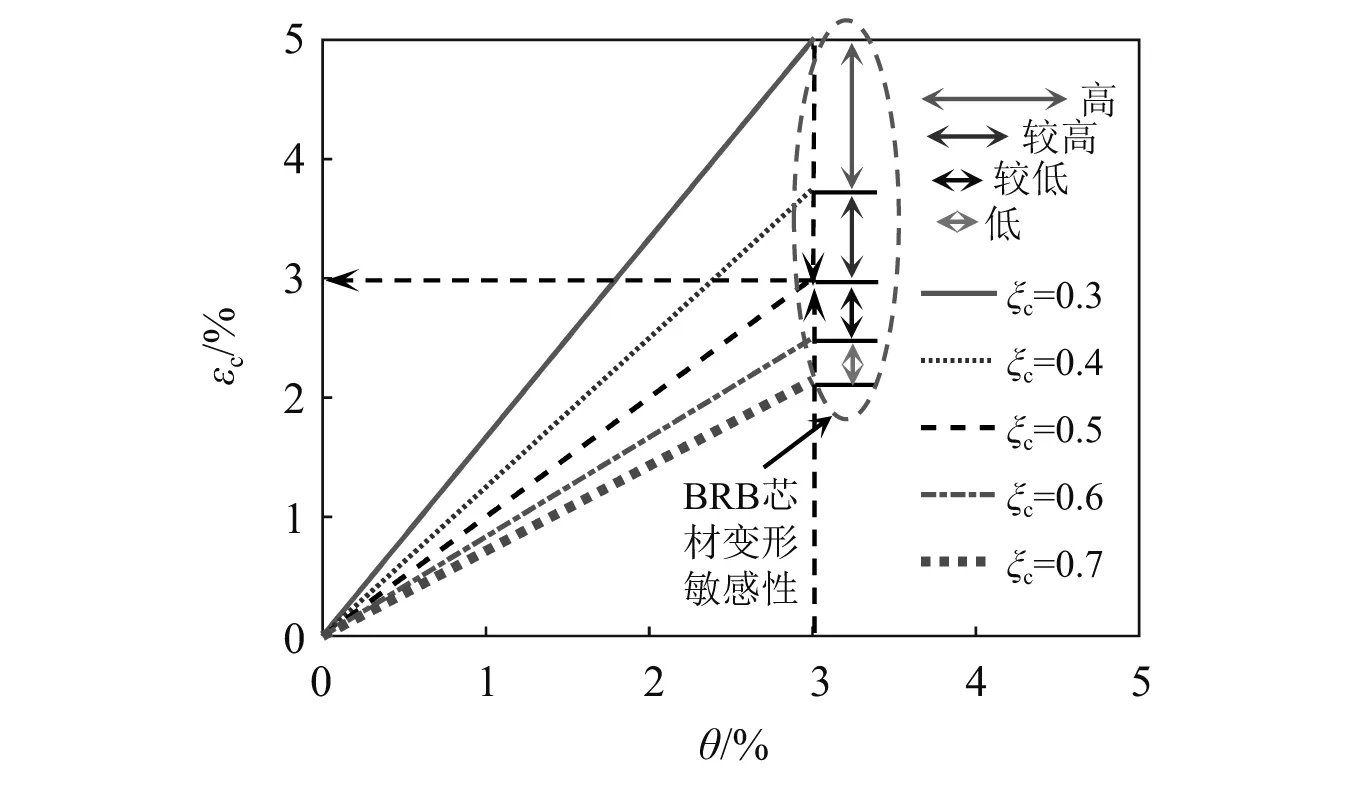
图7 BRB芯材应变与层间位移角关系曲线
2.2 BRB先于主体框架屈服条件
设框架产生水平变形Δ时,BRB芯材的应力为σ,则有下式
(15)
进一步将式(15)改写为
综上所述,八角枫水提液能够减轻CIA模型大鼠的炎症反应、关节软骨退变及骨破坏,其机制可能与下调血清IL-1β、TNF-α水平,调节OPG/RANKL/RANK系统平衡有关。但八角枫水提液对其他炎症因子及信号通路的影响尚需进一步探讨;此外,八角枫虽可治疗RA,但仍有患者误服致死的案例报道,故其安全用药剂量有待进一步明确,其相关用药知识也还需广泛普及。
(16)
由式(16)可知,当BRB屈服时,芯材应力σ=fy,此时对应的结构层间位移角θby为
(17)
要求BRB先于主体框架进入屈服耗能的条件为层间位移角θby为小于结构的屈服层间位移角θy,即
(18)
式(18)即为BRB结构设计过程中保证BRB先于主体框架进入屈服耗能的参数匹配条件。图8为BRB在不同材料屈服强度、布置角度及Qm取值下,BRB屈服时对应的结构层间位移角分布,从图中可知,其他条件相同时,采用低屈服点钢更易实现BRB先于主体框架屈服的目标,并且容易实现多遇地震屈服耗能;随着匹配系数Qm取值的增大,结构可在更小的层间变形下实现BRB屈服;对于混凝土框架结构,无法采用高强钢(如Q390钢)完成第Ⅲ类BRB产品的设计,当采用Q235钢时,在保证完成产品设计的基础上可通过调整合适的匹配系数Qm的取值及支撑布置角度φ实现多遇地震耗能;BRB布置角度为45°时,较其他布置角度更易实现先于主体框架屈服。
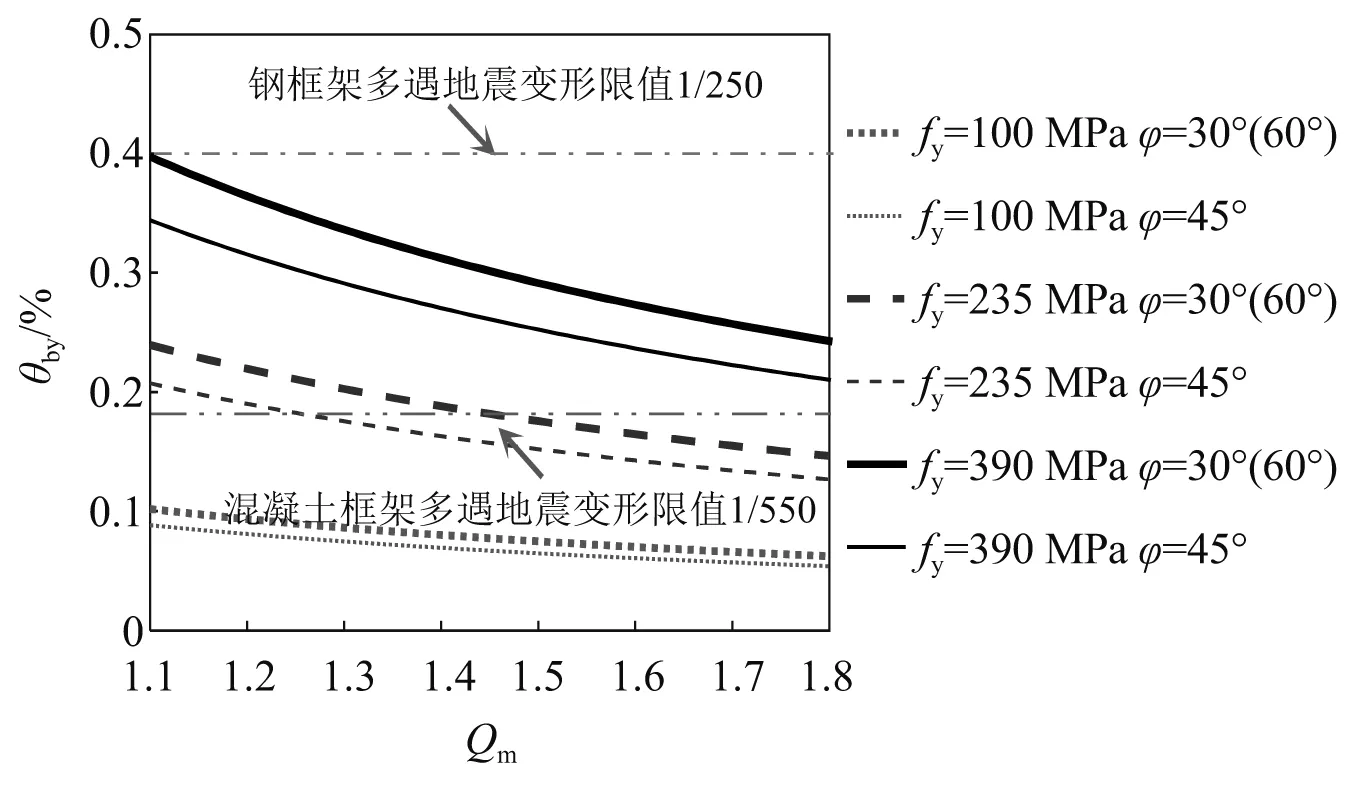
图8 BRB屈服时对应结构层间位移角分布
2.3 各水准地震作用下BRB屈服耗能条件
由前文的分析可知,设计人员可通过选用不同屈服强度钢材来实现BRB在不同水准地震作用下进入耗能状态,但目前可供选择的钢材种类有限,甚至当设计条件严苛时无法通过该方法有效的进行BRB的选型与设计,另一种可行的途径是通过调整BRB耗能段的长度(即调整ξc的取值),并配合选择合理的材料屈服强度实现BRB的工作性能目标。BRB在特定水准地震作用下屈服耗能的条件为
(19)
即
(20)
式中,θi(i=1,2,3,分别代表多遇地震、设防地震、罕遇地震)为结构在特定水准地震作用下的层间位移角。
为便于分析,记参数λi为结构在各水准地震作用下的实际层间位移角θi与相应的层间位移角限值[θi]之比,即
(21)
将式(21)代入式(20)得
(22)
通常,对于结构不同的性能目标及经济性要求,λi的取值范围约为0.6~1.0。式(22)即为BRB在特定水准地震作用下屈服耗能的判定条件,定义式(22)右边的表达式为屈服因子γ,即
(23)
由于GB 50011—2010《建筑抗震设计规范》中未对设防地震作用下结构的变形限值做出明确规定,设计人员也往往更加关注BRB在多遇地震作用和罕遇地震作用下的性能,下面分别对钢筋混凝土框架结构及多、高层钢结构体系在多遇地震作用下BRB是否屈服耗能的条件进行讨论。
从式(23)可以看出,屈服因子γ的取值越大,BRB越容易实现相应水准地震作用下的屈服耗能,反之,需将ξc的取值控制在较小范围内,即减小BRB耗能段的长度,这可能导致BRB在罕遇地震作用下延性性能不足而断裂破坏。当结构性能目标确定后,其在多遇地震作用下的层间变形即确定,屈服因子γ的取值仅受BRB布置方向与水平方向夹角φ及采用材料强度fy的影响。图9为式(23)中λ1取1,[θ1]分别取1/550及1/250时,屈曲因子γ随BRB布置角度及材料屈服强度的变化曲线,从图中可以看出,当BRB布置方向与水平方向的夹角为π/4时,在其他条件相同的情况下,式(22)最易满足,即最易实现在多遇地震作用下屈服耗能的设计目标;当BRB采用低屈服点钢进行设计时(如BLY100),对于钢筋混凝土结构体系和钢结构体系,γ的最大取值分别为1.96和4.12,由于ξc的取值总是小于1,因此低屈服点钢材BRB在多遇地震作用下屈服耗能的条件自然满足;当BRB采用高强钢进行设计时(如Q390),对于钢筋混凝土结构体系和钢结构体系,γ的最大取值分别为0.48和1.05,可见当采用高强钢时,钢筋混凝土结构体系较难实现BRB多遇地震耗能,而钢结构体系由于变形限值更大,合理设计下仍可实现BRB多遇地震耗能。同样,在设防地震作用下,可通过预估结构的变形,调整式(22)中ξc的取值及选用合适的钢材实现BRB在设防地震作用下的屈服耗能。屈服因子γ相当于给出了相应水准地震作用下BRB进入耗能时耗能段的最大长度限制。
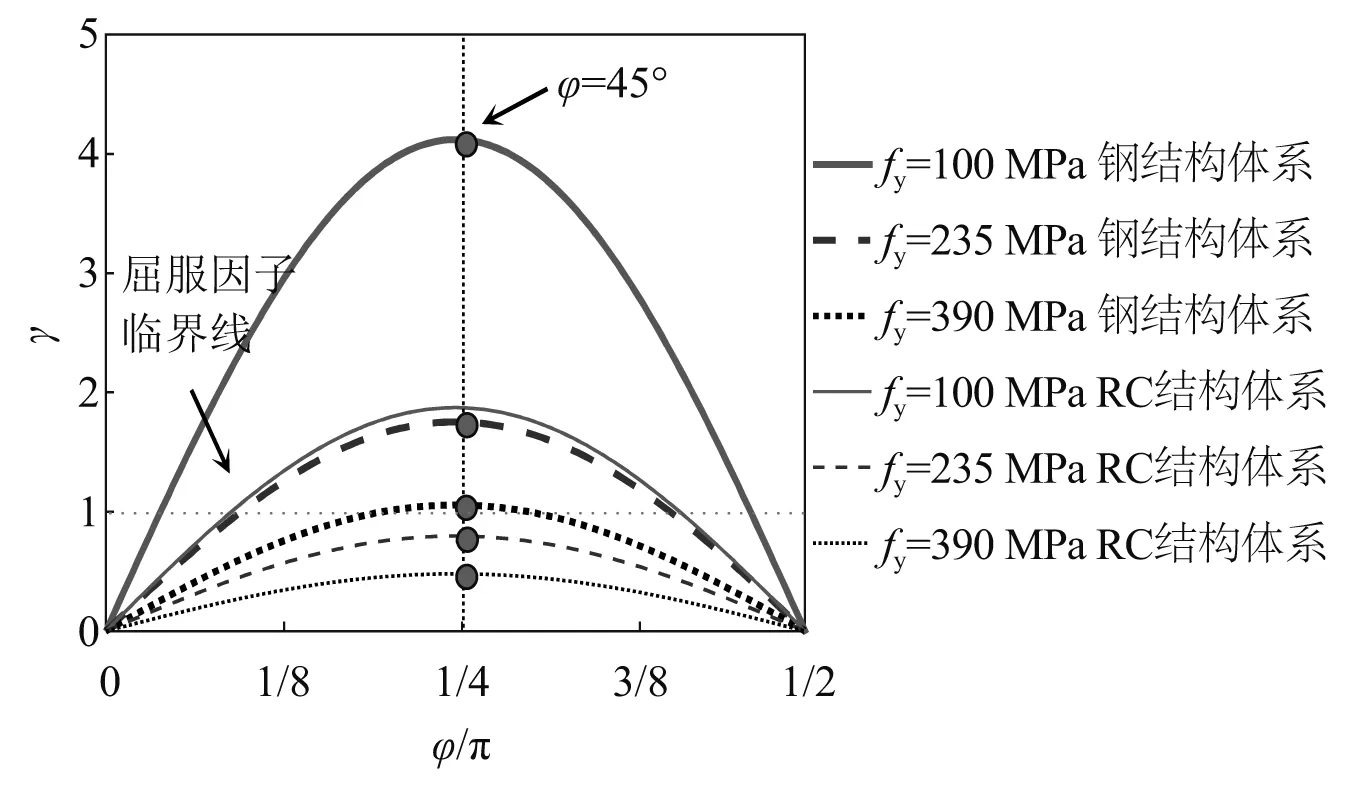
图9 屈服因子γ变化曲线
2.4 罕遇地震作用下BRB变形需求及安全保证条件
BRB越早进入屈服耗能状态即意味着罕遇地震作用下耗能段将产生较大的塑形应变,已有的研究成果表明[12],BRB耗能段的最大应变超过3%时,受压侧的摩擦力幅值增长较快,滞回曲线受压侧容易出现不稳定现象,且容易导致屈曲破坏,当BRB耗能段的最大应变控制在3%以内时,具有较为稳定的滞回耗能能力,因此,本文将3%的应变值作为BRB在罕遇地震作用下的安全保证条件,即
(24)
也即
(25)
BRB在罕遇地震作用下的变形能力并不一定是在结构弹塑性变形限值处满足延性需求即可,仍需考虑一定的安全余量,即估算BRB在罕遇地震作用下的延性需求时,应考虑结构在正常使用年限内可能遭遇的超过设防烈度的大地震作用。FEMA450规定[13], BRB的设计变形应按照最大层间设计变形的1.5倍确定,因此λ3的最大取值为1.5,定义式(25)右边的表达式为安全因子β,即
(26)
图10为钢筋混凝土结构体系([θ3]=1/50)、钢结构体系([θ3]=1/50)、框架剪力墙结构体系([θ3]=1/100)、剪力墙结构体系([θ3]=1/120)的安全因子β的取值范围,从图中可以看出,当BRB置角度为π/4时,其安全保证条件最为严苛,对于同一种结构体系,BRB采用不同钢材时,其安保证条件均为同一标准,这一点与屈服条件有所不同,主要是由于对于不同种类钢材的BRB均规定其在罕遇地震作用下的峰值应变不超过 3%,这相当于给出了BRB耗能段的最小长度限制。
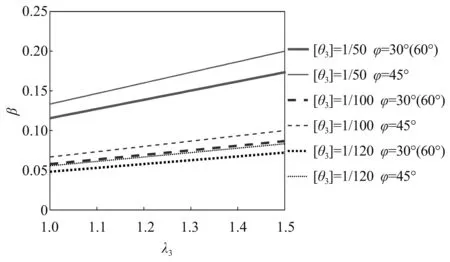
图10 安全因子β变化曲线
2.5 参数合理取值讨论
基于前文防屈曲支撑在特定水准地震作用下的屈服耗能条件及罕遇地震作用下的安全保证条件分析结果,既要实现BRB在特定水准地震作用下屈服耗能,又不至于在罕遇地震作用下断裂失效,则参数ξc应同时满足式(22)及式(25),即
(27)
分析式(27)可知,对于不同结构体系及BRB采用不同强度材料时,式(27)不总是成立,即可能出现不等式左边表达式取值大于不等式右边表达式取值的情况,也即BRB只能满足屈服条件和安全保证条件两者之一。不同结构体系及不同材料强度对应的式(27)左右两边表达式的取值见表2及表3。
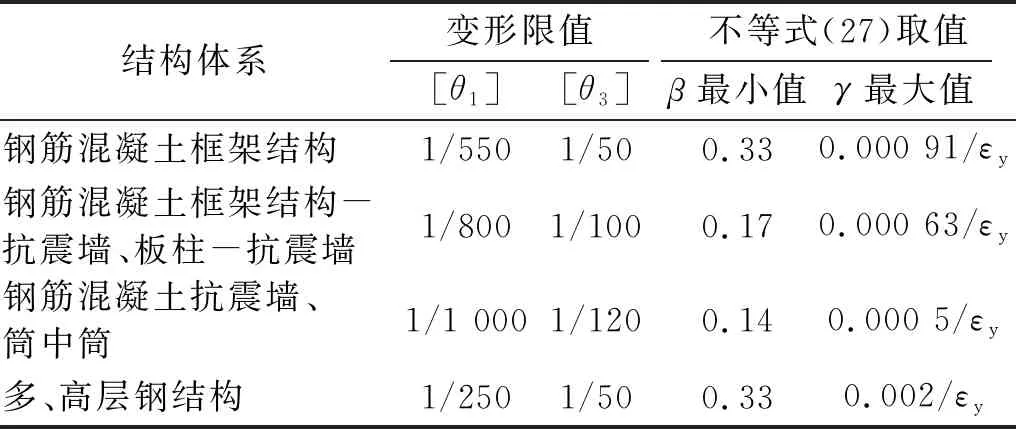
表2 不同结构体系对应安全因子β取值
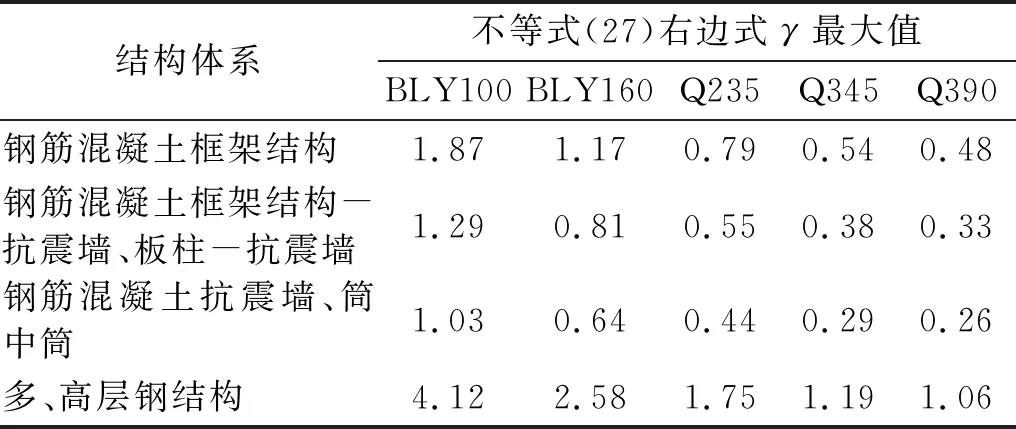
表3 不同材料强度对应屈服因子γ取值
从表2及表3中可以看出,当采用BLY100钢材时,理论上各结构体系通过合理设计均能实现BRB的多遇地震耗能并满足罕遇地震延性需求;当采用高强钢(如Q390)时,框架剪力墙结构及剪力墙结构则无法应用阻尼型BRB(第Ⅲ类),主要是ξc的取值受到限制而无法完成产品设计;对于多、高层钢结构体系,由于允许其在多遇地震作用下产生较大的侧向变形,即使采用Q390钢,通过合理设计也能实现阻尼型BRB的应用,并完成产品设计。总体上,钢材延性随其屈服强度的提高而降低,因此在应用BRB时应根据不同结构体系及不同的性能需求(刚度需求或耗能需求)合理选用。
3 BRB参数设计流程及算例分析
3.1 BRB产品参数设计流程
图11为基于前文分析结果的BRB参数设计流程图。值得注意的是,在参数设计过程中,等效钢支撑的应力水平κ的取值是非常关键的控制因素,其影响着BRB耗能段长度、芯材截面积及材料屈服强度的取值,从而影响着BRB能否实现既定的工作性能目标以及能否顺利完成产品设计。根据图11可确定BRB芯材屈服强度fy、耗能段长度Lc及截面面积Ac、过渡段长度Lt及截面面积At、屈服承载力Fy及屈服位移δy,基于以上参数可进一步按式(1)及式(6)计算连接段长度Lj及截面面积Aj,从而得到BRB连接段的刚度。
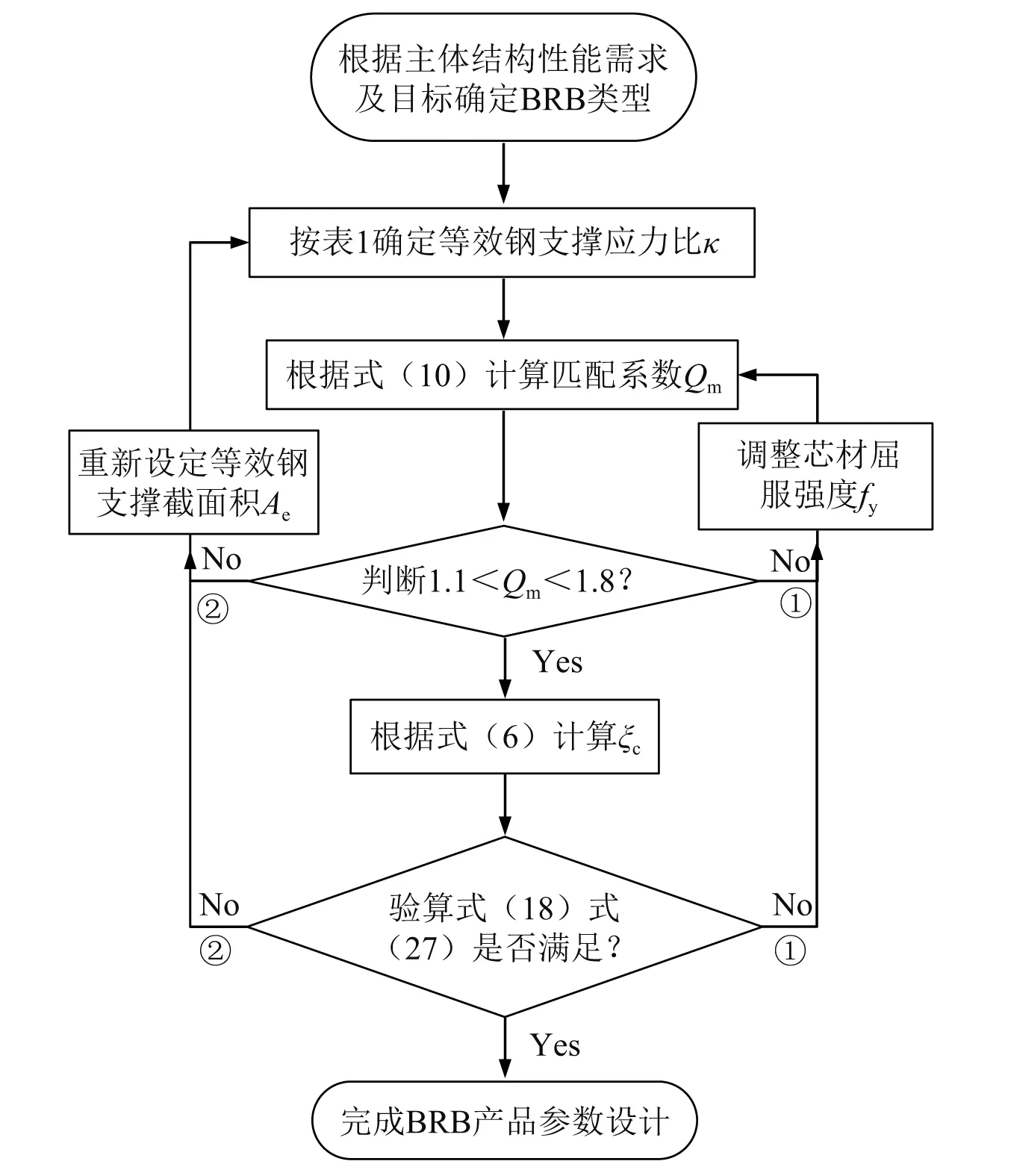
注:①表示优先执行;②表示按①执行仍不满足要求时执行。
3.2 算例分析
某框架结构共4层,底层层高4.5 m,标准层层高4.2 m,总高15.9 m,见图12(a),该结构抗震设防烈度为8度(0.2g),设计地震分组为第二组,场地类别为Ⅱ类,场地特征周期Tg=0.4 s。BRB的设计性能目标为多遇地震下弹性工作,设防地震及罕遇地震下屈服耗能,并作为结构的“保险丝”先于主体框架屈服,BRB的平面布置见图12(b)。按上述参数设计流程确定结构X向及Y向BRB各项参数,表4分别给出了X向及Y向各一根代表性BRB的产品设计参数,采用SAP2000软件建立非线性分析模型进行弹塑性时程分析验证所设计的BRB参数的合理性,其中BRB通过采用矩形截面钢杆并在钢杆上设置纤维塑性铰的方式来模拟其弹塑性力学行为,纤维塑性铰材料采用基于双线性本构关系的Q235钢材,滞回模型采用“BRB硬化模型”,纤维塑性铰的面积为BRB芯板截面面积。地震波根据GB 50011—2010《建筑抗震设计规范》对时程分析地震波输入的要求,基于地震动加速度峰值、有效持时及频谱特性进行选取。图13为X向及Y向BRB在选取的ChiChi地震波作用下的滞回曲线,从图中可以看出,BRB在多遇地震工况下保持弹性工作状态,在设防地震工况及罕遇地震工况下屈服耗能,X向及Y向BRB在罕遇地震工况下的最大轴向变形分别为13.36 mm,13.85 mm,即相应的BRB耗能段的应变分别为0.42%,0.41%,均未超过3%的安全保证条件,表明BRB在罕遇地震作用下可正常发挥耗能作用而不断裂失效,实现了设计的工作性能目标。图14为结构塑性铰的发展顺序,从图中可以看出,两方向BRB均先于梁、柱构件进入屈服耗能状态,成为结构的第一道抗震防线,非线性时程分析结果在一定程度上说明了文中BRB参数控制方法的有效性。
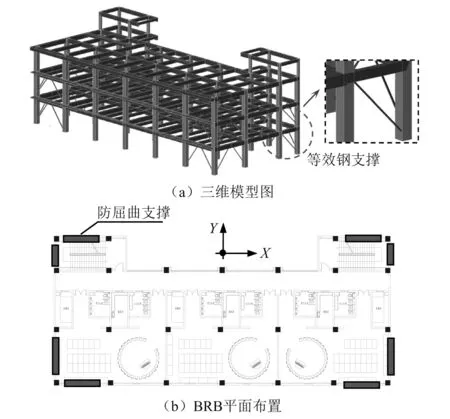
图12 BRB结构等效模型

表4 BRB产品设计参数
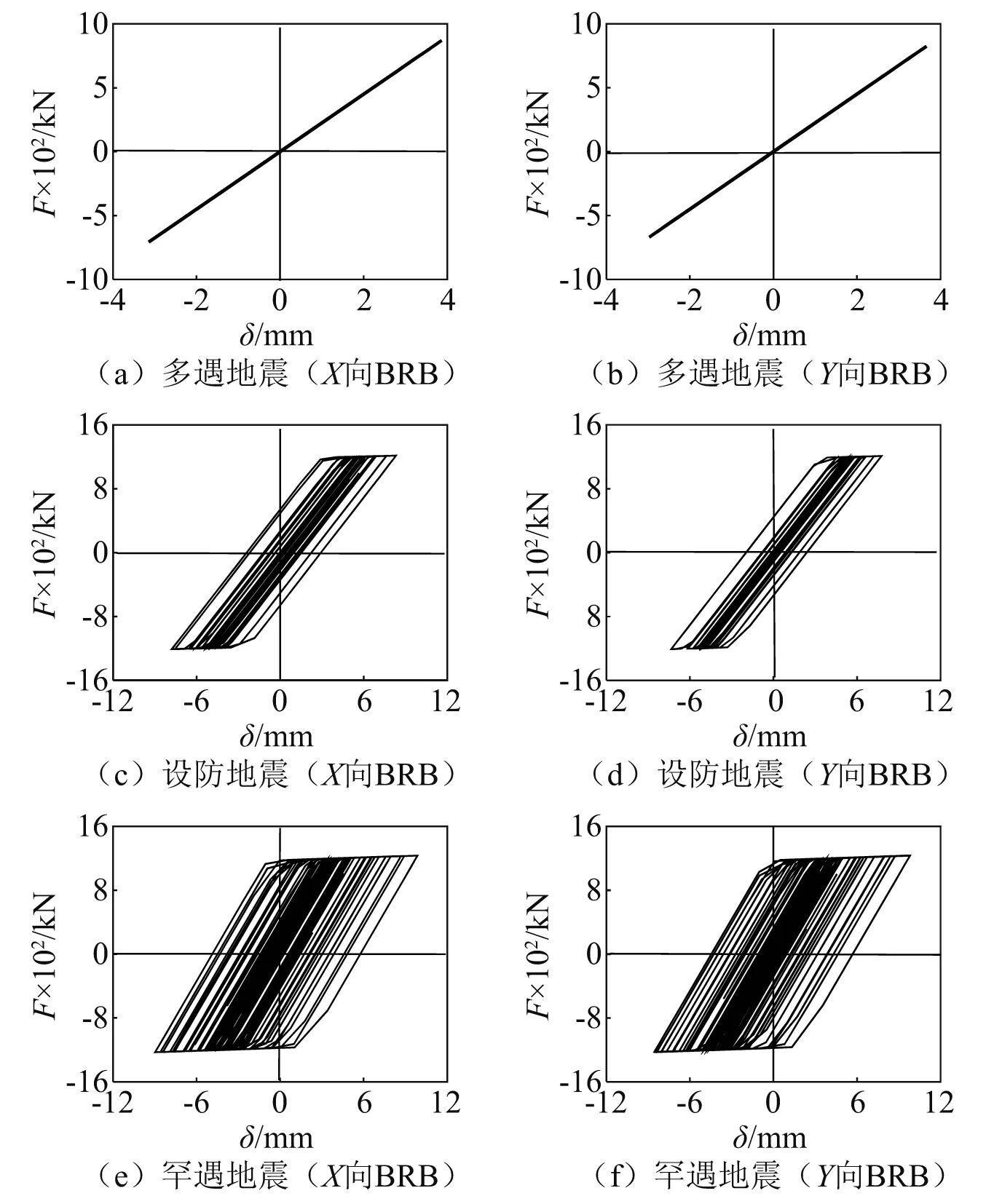
图13 各水准地震作用下BRB滞回曲线
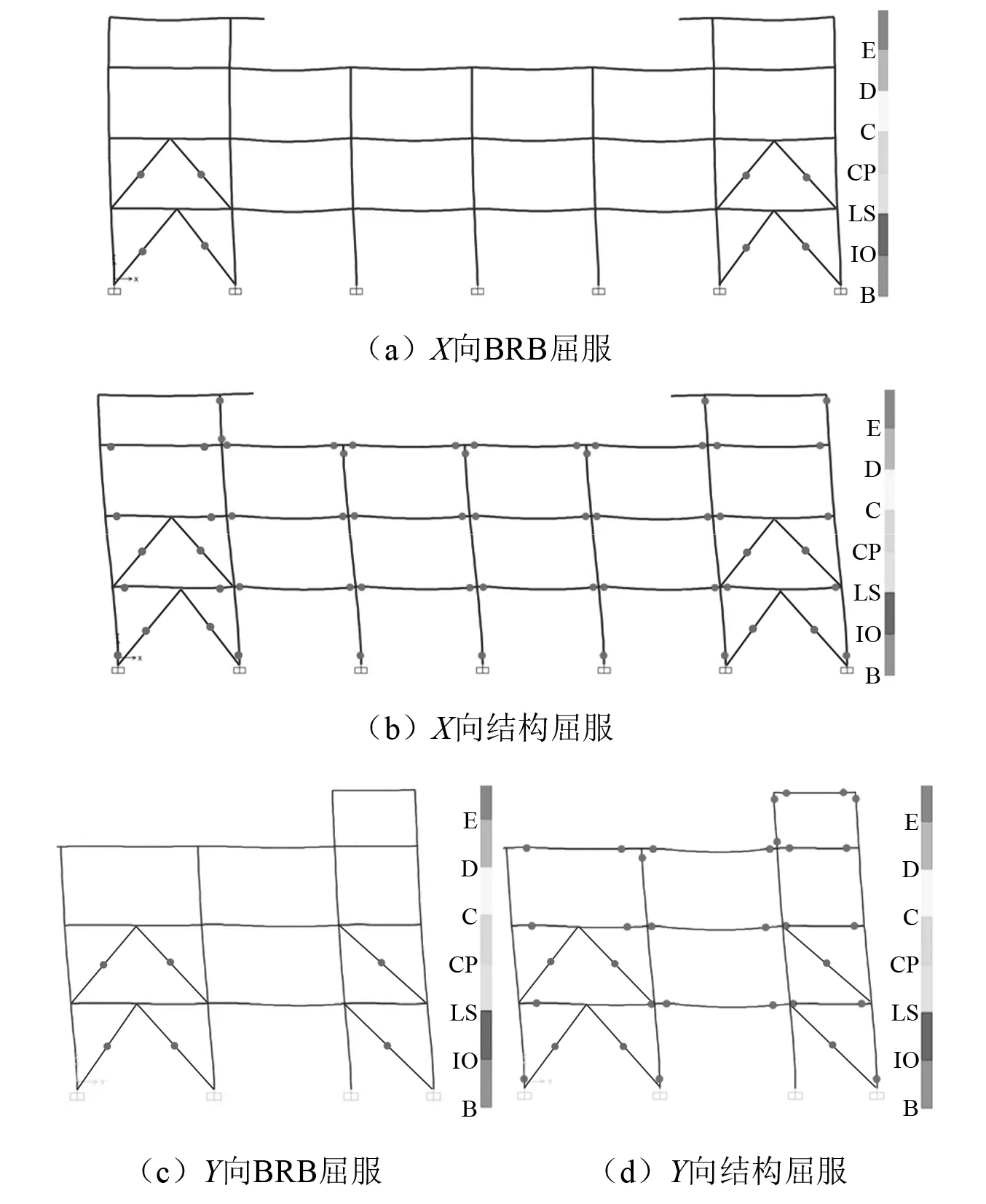
图14 结构屈服顺序
4 结 论
(1) 在进行BRB结构设计时,BRB的实际参数与等效参数间的合理匹配程度可通过系数Qm的取值进行调整,具体取值可参考文中建议数值。
(2) 在确定BRB等效参数过程中,等效钢支撑应力比κ是影响BRB产品参数合理性的关键因素,可根据BRB不同的性能目标按文中表1数值合理控制其取值。
(3) 相同结构变形下,BRB耗能段应变随其长度的增加而减小,采用低屈服点钢更易实现BRB先于主体框架屈服的目标,并且容易实现多遇地震屈服耗能。
(4) BRB材料确定的情况下,可通过式(25)控制耗能段长度的取值实现特定水准地震作用下的屈服耗能,并保证罕遇地震作用下的变形需求。
