内齿轮成形磨削砂轮架振动特性实验研究

2021-07-22苏建新聂少武

振动与冲击 2021年14期

苏建新，蒋闯，聂少武，程琛

(1. 河南科技大学机电工程学院，河南洛阳 471003； 2. 机械装备先进制造河南省协同创新中心，河南洛阳 471003)

近年来，随着高速列车、航空航天、工程机械以及海洋工程等领域的快速发展，对高精度内齿轮的需求量日益增多，同时对其性能也提出了更高的要求[1-2]。成形磨削是目前获得高精度内齿轮最有效的加工方法，因为具有高效率、通用性强、精度高等优点，越来越多的成形磨齿机被大量使用，提高其加工精度是目前齿轮行业的需求[3-4]。在内齿轮成形磨削中，磨削头作为磨齿机的磨削装置，用来保证砂轮主轴的回转精度、刚度和抗振性。砂轮架是磨削头的安装本体，用来支撑砂轮的旋转运动，保证砂轮高速回转的平稳性，减少磨削振动和噪音。但是受内齿轮加工空间的限制，要求砂轮架的结构尺寸尽可能小，同时砂轮架又是悬臂结构，受力工况恶劣，如何优化砂轮架的结构参数，保证其具有足够的强度和刚度,增大砂轮架的支撑稳定性，直接影响着内齿轮成形磨削精度和质量稳定性[5]。本文基于有限元技术对砂轮架进行静、动态特性分析，建立边界约束，对砂轮架结构参数进行多目标优化设计，优化砂轮架结构。通过磨削工况下的振动特性测试和数据分析，验证有限元仿真建模和结构参数优化的有效性和工程适用性。

基于上述原因，对岸桥起重机结构的有限元建模进行了分析，对模型的简化和约束处理作了探讨，的固有特性及动态响应。该研究对考虑动力设备(如计算起重机结构的模态，了解该型起重机的动力特性；并对岸桥起重机进行了模态和动态分析, 得到了系统电动机) 的振动可能传递给起重机引发的结构振动、控制和避免动力设备的振动引起的结构共振具有实际意义。

1 磨削头结构

数控内齿轮磨齿机主要由床身、底座、磨削头、数控滑台、数控回转台等组成。如图1所示，内齿轮磨齿机磨削头结构主要由砂轮架、电主轴、电主轴支座、磨头连接座、轴承、砂轮、皮带及带轮等组成，图2为该磨削头总成的三维模型。

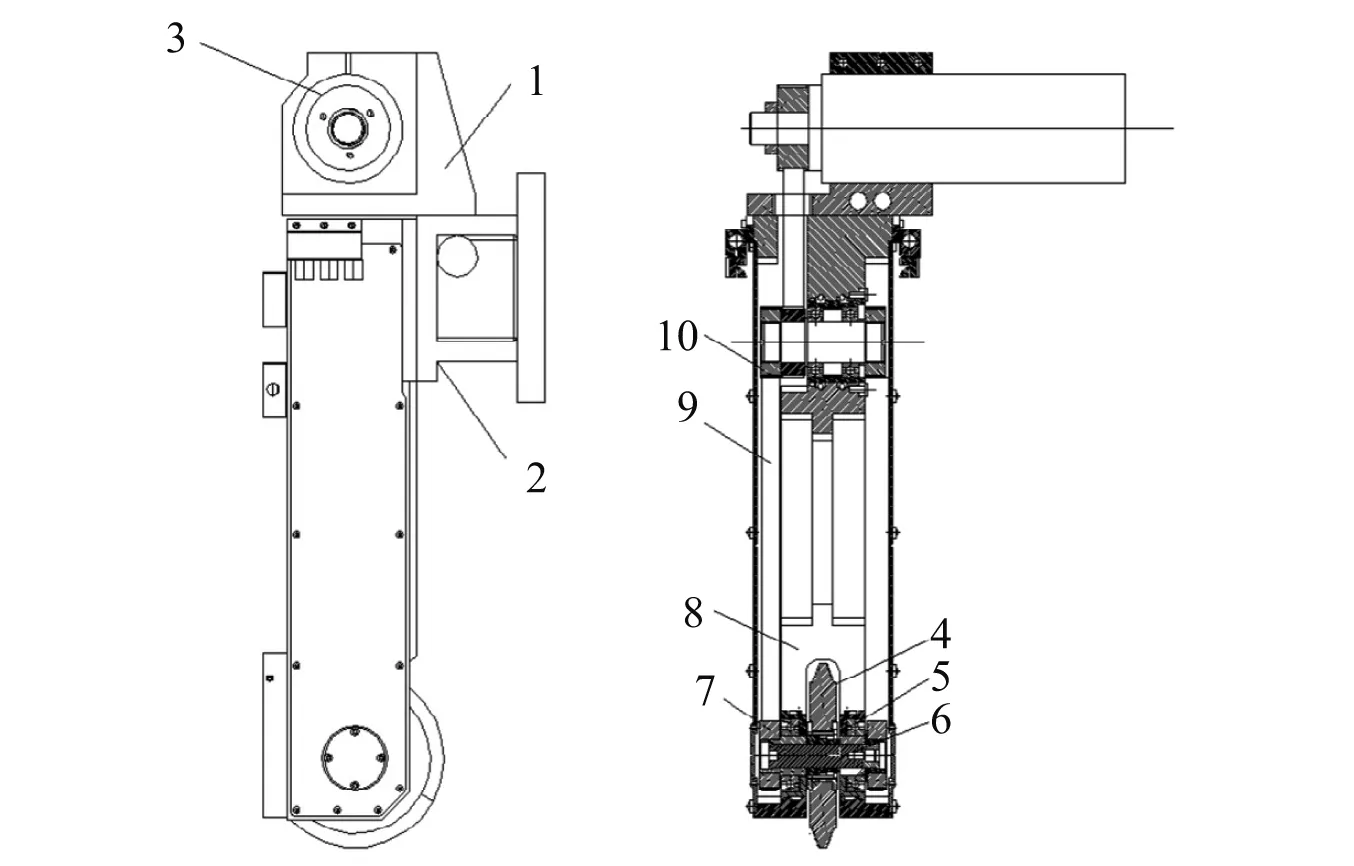
1.电主轴支座；2.磨头连接座；3.电主轴；4.砂轮；5.轴承；6.砂轮轴；7,10.带轮；8.砂轮架；9.皮带。

图2 磨削头总成三维模型

图3为砂轮架结构图。砂轮架是数控成形磨齿机的关键部件，砂轮架的强度和刚性对齿廓的加工精度、齿面粗糙度、砂轮寿命以及整机的性能都有直接影响。

图3 砂轮架

2 磨削头结构有限元分析

2.1 模态分析

应用Solidworks建立内齿轮数控成形磨齿机磨削头结构的三维模型，导入Workbench进行网格划分和有限元分析。砂轮架、磨头连接座、电主轴支架材料选用QT450-10，密度为7 100 kg/m3，弹性模量为182 GPa，泊松比为0.3，抗拉强度为450 MPa。轴承外套、内套、砂轮轴、砂轮端盖、中间带轮轴等材料为20CrMnTi，密度为7 800 kg/m3，弹性模量为207 GPa，泊松比为0.25，抗拉强度为1 080 MPa，砂轮架侧盖选用铝合金，密度为2 700 kg/m3，弹性模量70 GPa，泊松比0.3。磨削头三维模型导入有限元软件后，在材料库选取相对应的材料赋予给相应部件。采用六面体划分网格，分别包含275 624个节点和142 781个单元体，如图4所示。

图4 磨削头有限元模型

由磨削头装配模型可知，砂轮架与磨头连接座、电主轴支架通过螺钉固结在一起，砂轮架与侧盖通过螺钉固结。因此，砂轮架与磨头连接座、电主轴支架、侧盖之间定义为绑定接触。砂轮主轴与砂轮端盖、轴承内套之间有摩擦，所以定义为摩擦接触。所有接触都要定义接触刚度，过大的接触刚度可能会引起总刚矩阵的病态，而造成收敛困难，范围一般在0.01～10.00，通常取1.5或更大。阻尼取值范围通常为刚度值的0.1%～1.0%。设置分析模型的前6阶固有频率和振型，其固有频率如表1所示，各振型如图5所示。

表1 磨削头前6阶固有频率

由表1和图5可知结构的1阶频率为280.9 Hz，振型为砂轮架往Y方向弯曲变形，变形幅度较小；2阶频率为311.5 Hz，振型为砂轮架沿X方向弯曲变形；3阶频率为423.0 Hz，振型为电主轴支座沿X方向弯曲变形；4阶频率为659.0 Hz，振型为电主轴支座沿Y方向弯曲变形，变形幅度较大；5阶频率为1 052.0 Hz，振型为砂轮架沿Y的负方向变形；6阶频率为1 160.0 Hz，振型为砂轮架下部扭转变形。

图5 磨削头模态振型图

从磨削头的模态振型可知，当砂轮架的振动频率达到其固有频率时，其振动幅度会变大，这将对结构造成一定的破坏，因此，在实际加工过程中应避免砂轮架长时间处于共振频率下工作。

2.2 谐响应分析

谐响应分析是通过计算磨削头结构在少量频率下的响应，确定磨削头线性结构在承受随时间按正弦规律变化载荷时的稳态响应，获取响应曲线上峰值响应频率与响应幅值。为了准确预测磨削头在连续频率区间的振动特性，必需对磨削头结构进行谐响应分析。在对磨削头结构进行有限元模态分析的基础上，采用模态叠加法对砂轮架结构作有限元谐响应分析，实现材料属性、模型、网格划分等数据的调用。根据文献[6]可知磨削头主要受两个力，分别是切向磨削力Ft和法向磨削力Fn，磨削力由通过磨削力试验推导出的磨削力公式获得，这里取Ft为50 N，Fn为130 N，在磨削头结构主要受力变形处施加载荷。在设置中Range Minimum为0，Range Maximum为2 000 Hz。模型的应力响应曲线如图6所示。由图6可知，在200～500 Hz，800～1 200 Hz这两个频率区间，应力响应比较大，X，Y，Z三个方向的应力峰值分别为11.42 MPa，2.094 MPa，14.545 MPa，模型在Z方向的应力响应最大，该方向是主要响应方向。

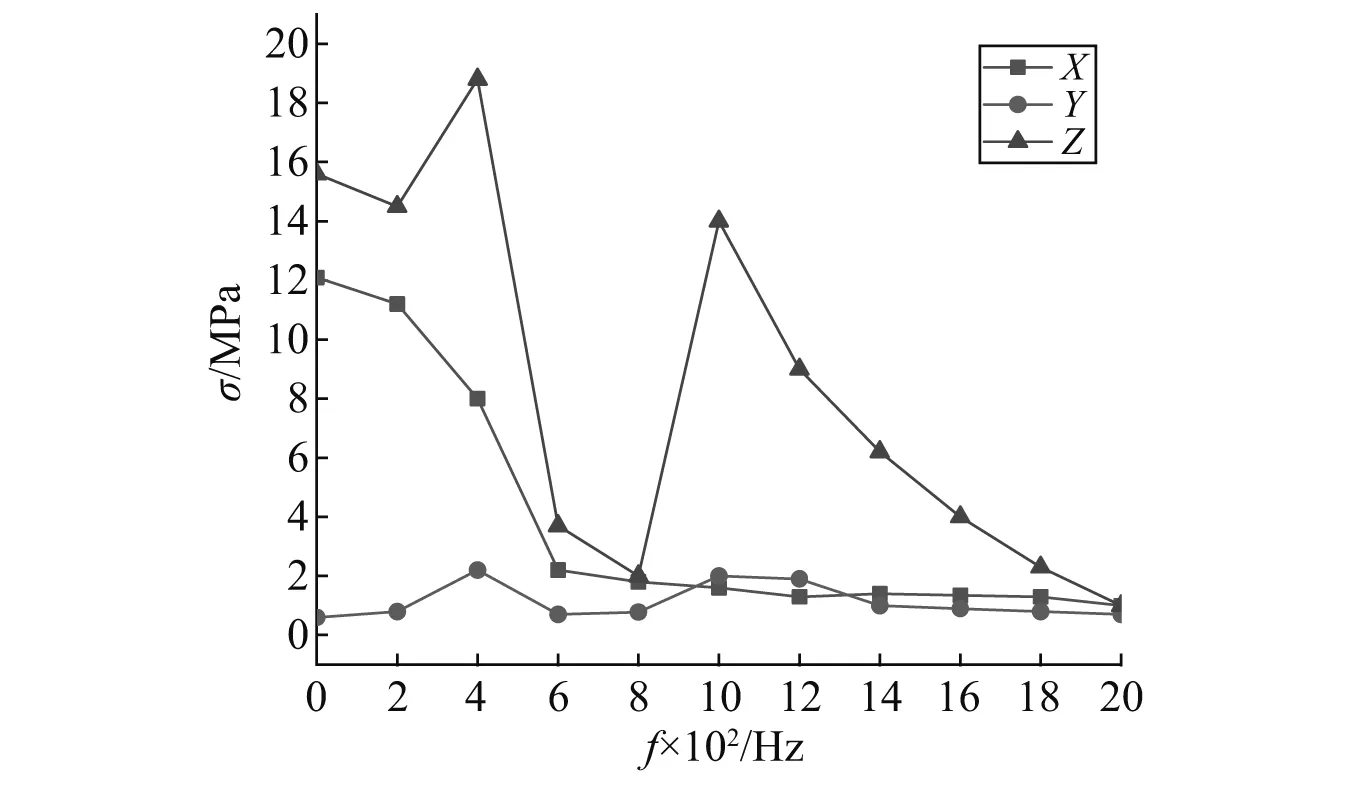
图6 应力响应曲线

模型的位移响应曲线如图7所示，由图7可知，在200～500 Hz，800～1 200 Hz这两个频率区间，位移响应比较大，X，Y，Z三个方向的位移峰值分别为2.07 μm，0.37 μm，3.19 μm。磨削头的工作频率在200～500 Hz，800～1 200 Hz这两个区间内时，位移值较大，会对磨齿加工精度和可靠性造成影响。有必要对磨削头结构进行改进，改善磨削头的幅频特性，减小磨削头幅频响应的位移峰值。

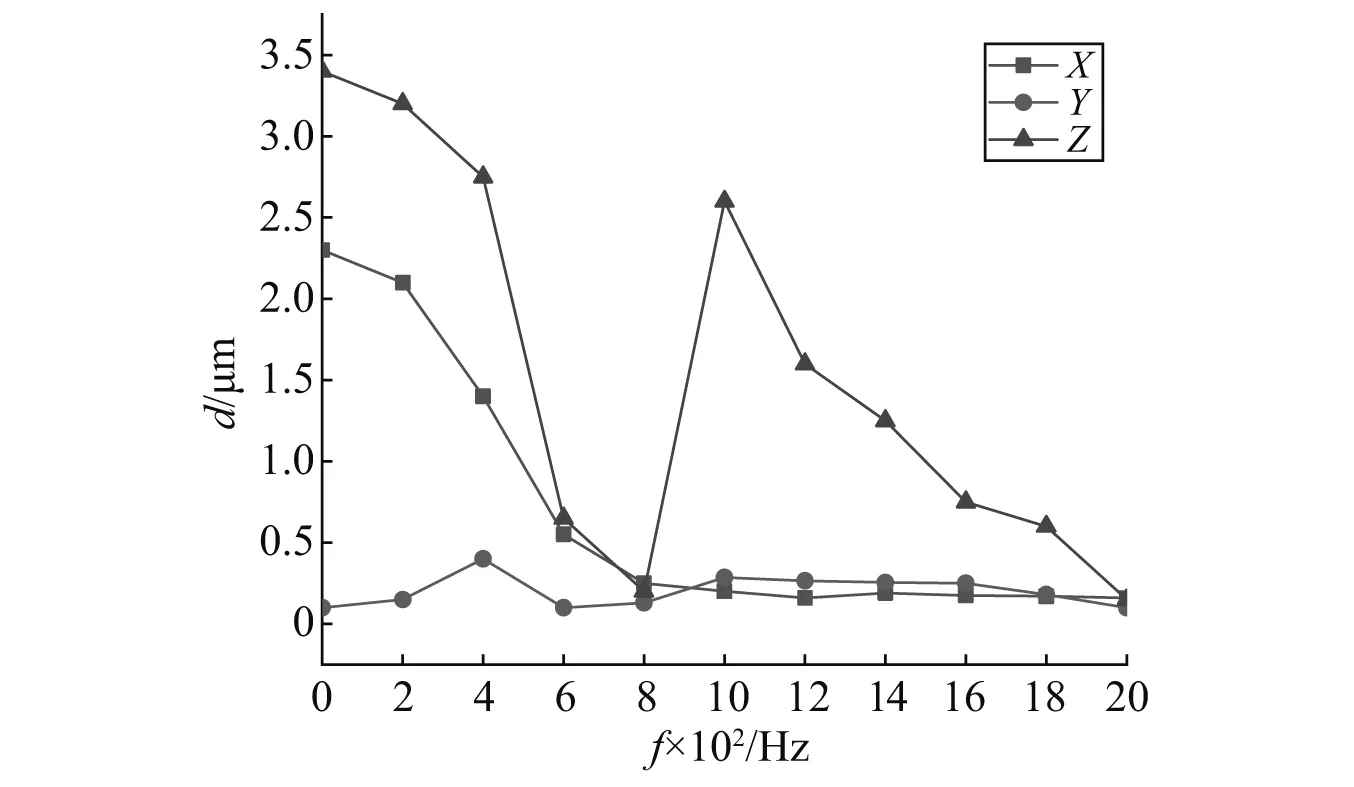
图7 位移响应曲线

3 砂轮架优化设计

根据第2章的分析，砂轮架是磨削头结构里的薄弱环节，且砂轮架的强度和刚度对磨削头整体结构的动态性能及安全性有显著影响，本节采用ANSYS Workbench软件中Design Exploration模块下的响应曲面优化分析工具(response surface optimization，RSO)对砂轮架进行优化。

3.1 砂轮架参数化模型

为了提高砂轮架的性能，这里着重对其进行基于响应面法的多目标优化[7-9]。参数分布情况如图8所示，P6，P4，P5依次为凹槽一的长、宽、高，P3，P2，P1依次为凹槽二的长、宽、高，具体的参数选取及取值范围，如表2所示。

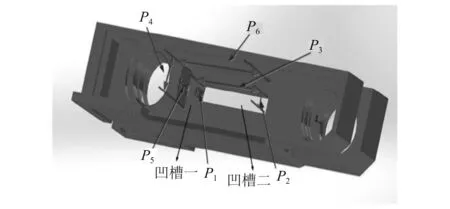
图8 砂轮架参数结构图

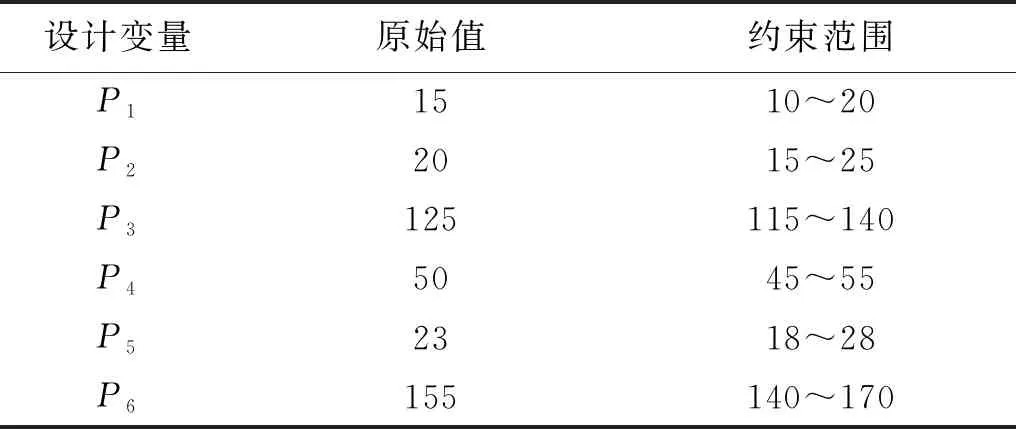
表2 砂轮架结构参数变量取值

将表2中砂轮架的设计变量运用数学方法的表现形式，可以表示为

x=[x1,x2,x3,x4,x5,x6]T=[P1,P2,P3,P4,P5,P6]T

(1)

式中，Pi为砂轮架的设计变量。

砂轮架的约束范围可以表示为

ui≤xi≤vi,i=1,2,3,…,6

(2)

式中，ui和vi分别为设计变量下限和上限。

砂轮架优化设计目标是在减小砂轮架的体积的同时，使其最大变形和最大应力最小化，故三个目标函数分别定义为

(3)

式中：M(xi)为砂轮架的质量； Defmax(xi)为砂轮架的最大变形量； Stfmax(xi)为砂轮架的最大应力值。

砂轮架的设计变量、约束条件和目标函数的优化设计数学模型为

(4)

3.2 灵敏度分析

通过灵敏度分析的结果可以看出哪些优化参数对结构的性能指标具有较大的影响作用。运用ANSYS中Design Exploration模块对砂轮架进行参数优化，将砂轮架的质量、最大等效应力、最大位移及安全系数作为优化目标，将其尺寸作为优化设计变量，采用中心复合实验设计确定仿真试验样本点，基于上百组仿真设计样本点的求解结果，获得P1，P2，P3，P4，P5，P66个设计变量对优化目标的灵敏度，图9为6个设计变量对砂轮架4个优化目标的灵敏度直方图。

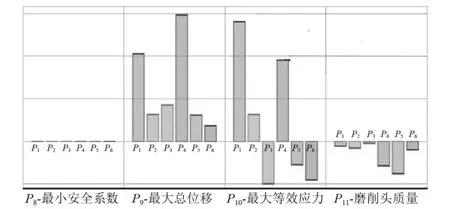
图9 砂轮架灵敏度直方图

由图9可以看出，在对砂轮架进行尺寸优化设计时，P1，P4对砂轮架总位移灵敏度较高，其中P1，P4参数值越大则总位移越大；P1，P4对砂轮架最大等效应力的灵敏度较高，且其参数值越大则应力越大；P4，P5对砂轮架质量的灵敏度较高，其参数值越大则质量越小。基于图9分析结果，需要重点关注P1，P4，P5参数值对砂轮架总位移、等效应力、质量的影响。

3.3 响应曲面分析

响应曲面法是通过对多元二次回归方程的分析来寻求最优参数，解决多变量问题的一种统计方法[10-11]。在对砂轮架灵敏度分析的基础上，对砂轮架性能影响最大的P1，P4，P5进行响应曲面分析，图10为P1，P4对砂轮架最大等效应力的响应曲面，图11为P1，P4对砂轮架总变形的响应曲面，图12为P4，P5对砂轮架质量的响应曲面。由图10和图11可以看出，砂轮架最大等效应力与总变形随着P1，P4的增大呈缓慢增大趋势；由图12可以得到，砂轮架的质量随着P4，P5的增大呈快速减小趋势。

图10 P1，P4对等效应力的响应曲面

图11 P1，P4对总位移的响应曲面

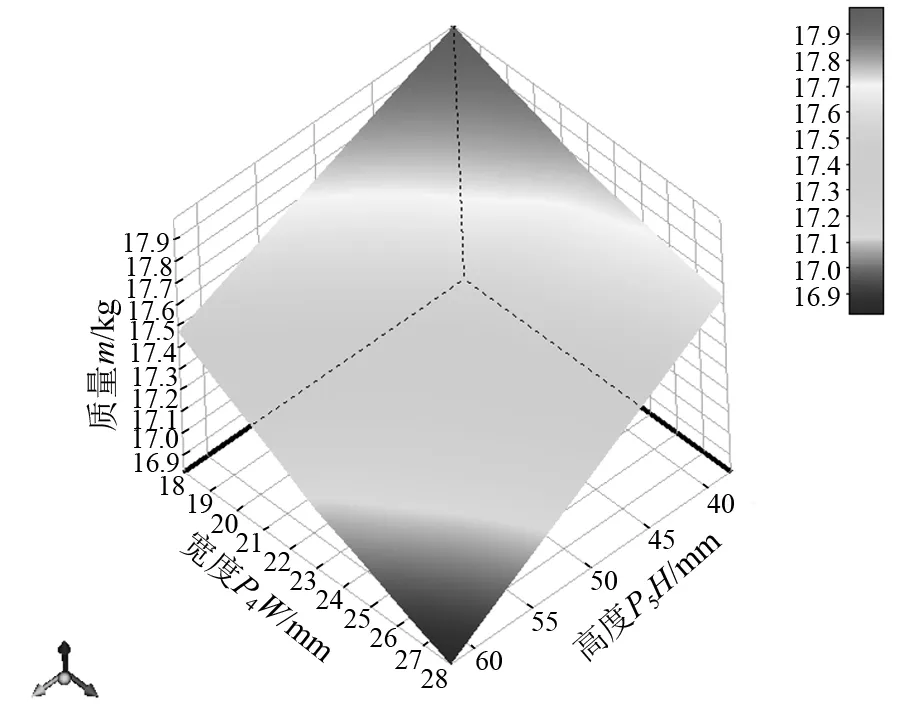
图12 P4，P5对总质量的响应曲面

图13～图18描述了P1，P4，P5等参数对等效应力、总质量、总位移的影响规律。由图13和图14看出，P1，P4与等效应力之间呈现不规律的变化。由图15和图16看出，随着P1和P4的增大，总位移也随着增大。由图17和图18看出，随着P4和P5的增大，总质量随着减小。

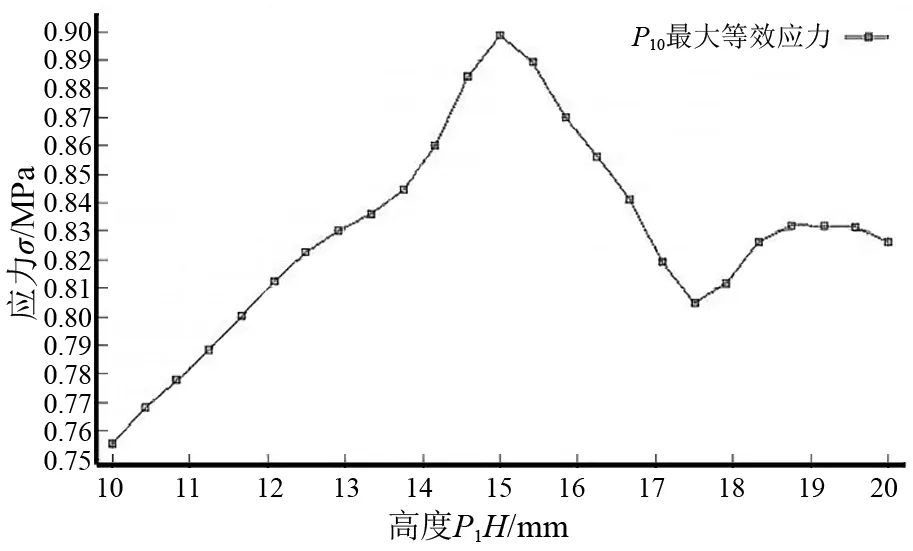
图13 P1-应力变化曲线

图14 P4-应力变化曲线

图15 P1-位移变化曲线

图16 P4-位移变化曲线

图17 P4-质量变化曲线

图18 P5-质量变化曲线

3.4 优化结果分析

根据砂轮架响应曲面和灵敏度参数优化结果，在RSO模块施加约束条件和多个约束目标，最后得到满足约束条件的三组最优设计方案，如图19所示，表3为三组最优设计方案修正后的具体数据。

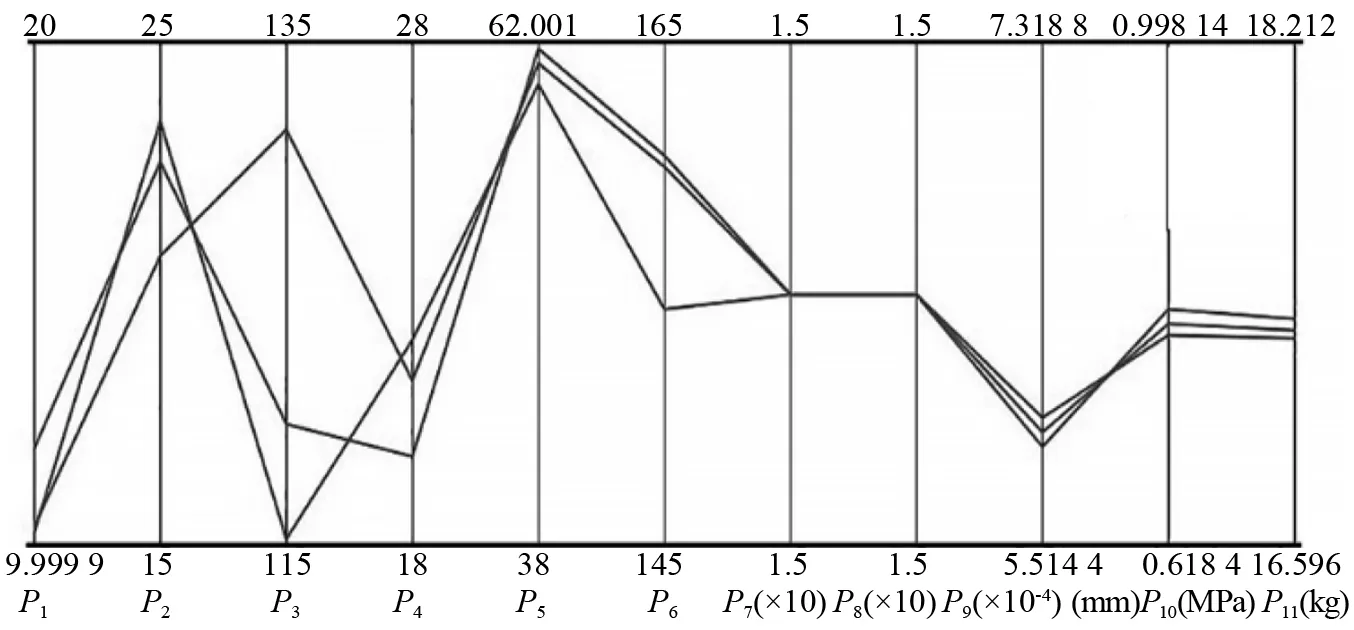
图19 三组候选方案

表3 砂轮架参数修正后尺寸

对优化后的磨削头模型进行模态分析和谐响应分析，优化前后磨削头的动态性能对比情况如表4所示。通过表4可以看出，优化后的磨削头前6阶固有频率均得到一定程度上的提升，其中1阶固有频率提升较大，相较于优化前磨削头结构的固有频率增加了4.97%，这对于增强机床的抗振性能具有重要意义。

表4 优化前后磨削头的动态性能对比

优化后模型的应力响应和位移响应，如图20和图21所示，其中优化后模型在三个方向的最大应力响应分别为7.412 MPa，0.894 MPa，9.345 MPa，与优化前相比分别减小了35.0%，57.3%，35.8%；优化后模型在三个方向的最大位移响应为1.324 8 μm，0.296 0 μm，2.679 6 μm，与优化前相比分别减小了36%，20%，16%。

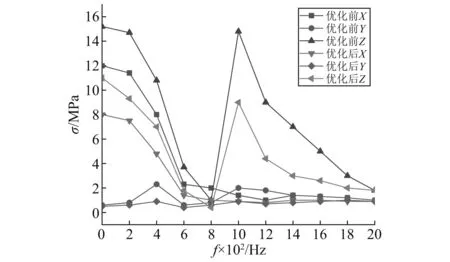
图20 应力响应对比

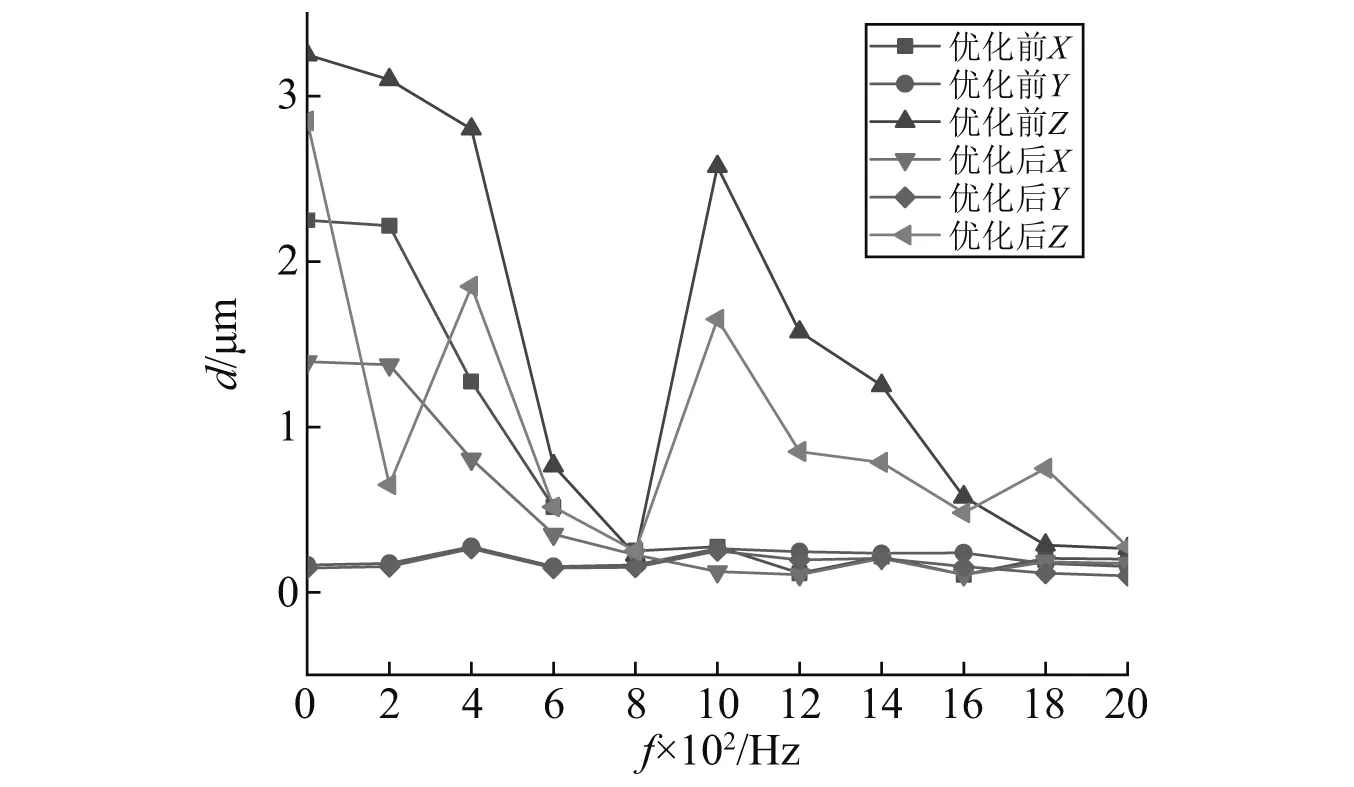
图21 位移响应对比

4 磨削头振动试验分析

为了验证磨削头结构优化的有效性，分别对优化前后的磨削头进行了磨削工况下的振动试验。首先搭建测试平台，测试平台主要是采集磨削头结构在磨削加工中的振动加速度信号，测试平台硬件主要有：电脑、振动加速度传感器、多通道数据采集卡、数控成形磨齿机，加速度传感器的灵敏度为1 000 mV/g, 量程0.01～49.99g；数据采集卡选用的是一款8通道24位USB电压信号采集卡。测试平台如图22所示。

图22 磨削头振动测试平台

为准确反映磨削头的振动情况，选择测点的位置靠近旋转支撑点振源，测点分布如图23所示。

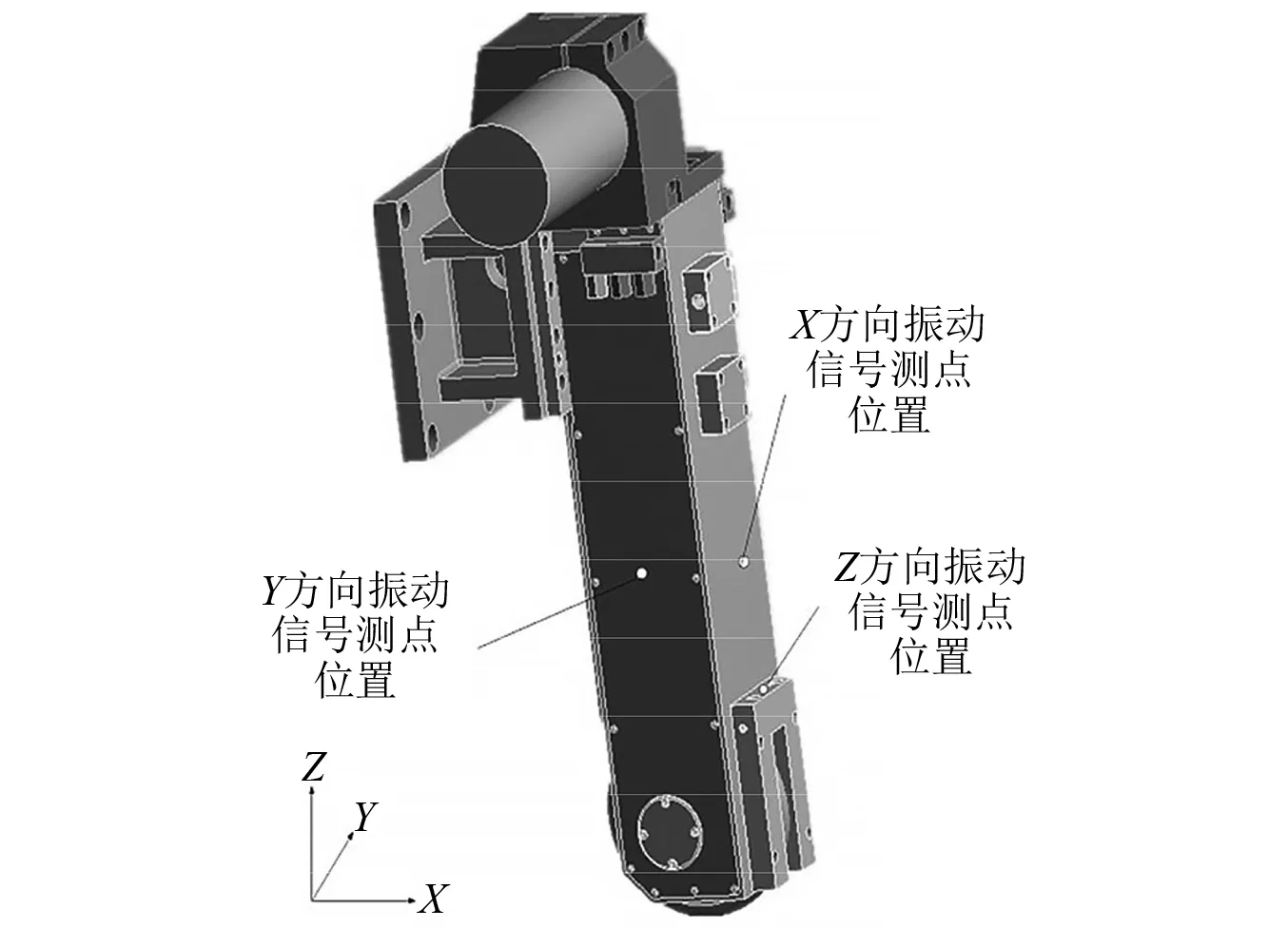
图23 磨削头振动试验测点位置分布

取两种磨削工况下的振动信号进行对比：工况一，主轴转速4 800 r/min，磨削深度ap为0.02 mm，进给速度2 400 r/min；工况二，主轴转速6 000 r/min，磨削深度ap为0.02 mm，进给速度2 400 r/min。优化前后的振动情况如图24～图27所示。

图24 优化前磨削头在工况一下振动信号

图25 优化后磨削头在工况一下振动信号

图26 优化前磨削头在工况二下振动信号

图27 优化后磨削头在工况二下振动信号

由图24和图25看出，优化前磨削头在工况一的振动加速度范围在±0.06g内，优化后磨削头在工况一下的振动加速度范围在±0.03g内；由图26和图27看出，优化前磨削头在工况一的振动加速度范围在±0.09g内，优化后磨削头在工况一下的振动加速度范围在±0.06g内。可以发现，优化后的磨削头结构在相同磨削工况下振动加速度信号比优化前的小。

时域信号不能很直观的显示出整个运动过程中的振动情况，所以需要对频域信号也进行处理分析。对时域信号进行傅里叶变换得到频域信号，可以获得信号的频率成分、相位变化，进而进行频谱分析。

优化前后的振动频谱图如图28～图31所示。