基于循环频谱相干和DCNN的隔膜泵单向阀故障诊断方法研究

冯泽仲， 熊 新， 王晓东

(1. 昆明理工大学 信息工程与自动化学院，昆明 650500；2. 云南省矿物管道输送工程技术研究中心，昆明 650500；3. 昆明理工大学 云南省人工智能重点实验室，昆明 650500)

矿浆管道是一种新型物料运输方式，有效解决了矿源地输送困难的问题，具有节能、环保、廉价等优点。作为矿浆管道输送的核心动力设备，隔膜泵能够在高压、高温及高腐蚀等工况下较好的输送浆体介质[1]。其中，由于单向阀受较高的工作频率及复杂机理的影响，致使其成为隔膜泵中最易发生故障的部件，因此，开展单向阀故障诊断技术的研究对保障系统安全可靠运行，避免重大事故的发生具有非常重要的意义[2]。

目前，随着信号分析、数据挖掘及人工智能等相关技术的迅猛发展，基于数据驱动的智能故障诊断方法逐渐成为该领域的重点研究方向[3]。众所周知，该诊断过程通常包括两个主要步骤：通过信号处理技术实现特征的提取；使用分类算法完成故障的识别。传统的分类技术，如人工神经网络(artificial neural network, ANN)、支持向量机(support vector machine, SVM)[4]和k-NN[5]等，由于其实现速度快、分类性能好而被广泛采用[6]。然而，受限于浅层的体系结构，它们很难从原始的高维输入中有效地学习差异性特征[7]。

近年来，深度学习凭借其强大的非线性建模以及特征表征能力，在机械设备故障诊断方面表现出了极大的潜力[8]。其中，深度卷积神经网络(deep convolutional neural networks, DCNN)以其优秀的局部特征提取能力和灵活的结构得到了广泛的应用[9]。高佳豪等[10]利用自参考自适应消噪技术对信号进行周期和随机预处理，将分离出的信号送入一维卷积神经网络中进行特征学习，提出了一种新的齿轮箱故障诊断方法。李恒等[11]对收集到的振动信号进行短时傅里叶变换，然后将得到的时频谱样本送入构建的卷积神经网络进行学习，最后将训练好的模型应用于轴承的故障诊断当中。Wen等[12]将原始的一维时序信号转换为二维灰度图，以得到适用于二维卷积神经网络的输入数据，提出了一种电机轴承的故障诊断方法。虽然以上深度学习方法均在故障诊断中展现出了良好的性能，但大都未能充分考虑实际工况环境下异常干扰对诊断性能的影响。Chen等[13]验证了将领域知识和深度学习结合的方式在噪声环境下轴承故障诊断中的优越性，考虑到单向阀工作在强干扰环境下，背景噪声容易将重要特征信息淹没，因此，有必要在网络学习之前将领域知识融入于特征提取过程，以增强诊断网络输入的特征表示。

当单向阀发生故障时，其动力学行为发生的变化难以通过现有特征提取方法有效表示，从而限制了最终的诊断结果。为了克服这一缺点，本文首先利用循环平稳特性分析了隔膜泵单向阀不同健康状况存在时的物理特性，循环平稳性可以看作为一个具有隐含周期性的随机过程，当由往复式部件组成的系统出现故障时会改变这一特性，通常又会在运行周期内通过另一种节奏释放能量，这种现象通常会在机械信号中产生瞬态信号，继而可能携带有关机器运行状况的关键信息。因此，循环平稳性常被用来解决往复式机械中的故障检测问题[14-15]。其中，循环频谱相干(cyclic spectral coherence, CSCoh)已被证明是循环平稳分析的有效工具，它通过将信号潜在的循环平稳调制信息表示为频域的双变量映射，从而揭示调制频率及其谐波，可以很好的将循环信息表征在双频谱图中[16]。而循环频谱相关(cyclic spectral correlation, CSC)作为实现CSCoh的重要步骤，其检测的精确程度直接影响了CSCoh的检测效果。为了提升循环平稳信息的检测能力和效率。Antoni等[17]将循环调制频谱和平均循环周期图[18]两者有机的结合，提出了快速循环相关谱计算方法[19]。

综上所述，本文针对实际工况环境下，隔膜泵单向阀的振动特性很容易被强烈的背景噪声和其他干扰成分所掩盖，从而限制最终诊断性能的问题，提出将CSCoh和DCNN结合的隔膜泵单向阀故障诊断方法，首先利用快速循环相干谱构建出大量带标签的样本；然后利用设计的DCNN网络对隔膜泵单向阀故障进行识别。通过构建的领域知识增强的深度故障诊断模型，大大降低了小样本数据集情况下深度卷积神经网路的学习难度，实现了隔膜泵单向阀的精确智能诊断。

1 循环相干谱分析

1.1 循环频谱相干

循环平稳信号代表了在时间上保持恒定统计行为的物理现象。它由周期机制产生，且包含了其他的信息，这些信息通过隐藏的周期特性所携带。通常可利用循环平稳的二阶特征来表征这种信号隐藏的周期性行为。对于一个循环平稳信号x(t)，可以将循环平稳的二阶矩分解为周期为T的瞬时自相关函数(auto correlation function, ACF)，描述为

R2x(t,τ)=R2x(t+T,τ)=

E{x(t+τ/2)x(t-τ/2)*}

(1)

式中：上标*为复共轭；τ为时滞，该ACF的傅里叶系数对应于循环ACF，描述为

(2)

式中，α定义为循环频率。从式(2)可以看出，循环ACF表示了α相对于时滞信号R(t,τ)的傅里叶系数。

循环平稳性的二阶统计描述符称为循环频谱相关，可通过在循环ACF上进行傅里叶变换来估计，如式(3)所示

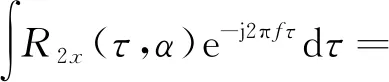
∬R(t,τ)e-j2π(ατ+fτ)dtdτ

(3)

对式(3)进行数学上的分析，可以等效为在时间t上的傅里叶级数，和在时滞τ上的傅里叶变换，其通过瞬时自相关函数的双离散傅里叶变换表示，如式(4)所示

(4)

式中：Fs为采样频率；tn=n/Fs；τm=m/Fs。对于循环平稳信号，CSC表现为在频率f上连续，在循环频率α上离散的特征信号，即信号相对于“调制频率”α和“载波频率”f的分解。

(5)

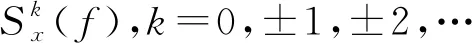
然后，可以将标准化过程添加到CSC中，以最大程度地减少不均匀分布，这被称为循环频谱相干，如式(6)所得

(6)

CSCoh用于测量两个频谱分量之间的关联程度，可以解释为一个白化信号的CSC，它趋向于使具有不同能级的区域均衡，从而放大微弱的循环平稳信号。

此外，在所有频率f上的频谱相关性积分对应于信号平方的期望值进行傅里叶变换。因此，它相当于信号的平方包络谱。而与平方包络谱相比，增强包络谱(enhanced envelope spectrum, EES)由于集成了复数值，因此EES可以更好地增强非零循环分量。在给定频带[f1;f2]上测量的EES定义为

(7)

1.2 循环相关谱快速计算方法

目前，CSC的一种流行估计方法是通过平均循环周期图(averaged cyclic periodogram, ACP)获得,对于一个对称的数据窗口w[n]，其定义为

(8)

式中：Xw(i,f)为对时间索引i和频率f的Gabor滤波；Nw为短时傅里叶变换(short-time Fourier transform，STFT)的窗口长度；K=(L-Nw+R)/R表示当信号长度为L时，移位窗口长度为Nw的R个样本总块数。通过均方的概率极限计算可得

(9)

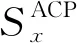
对于循环平稳信号的另一种表述方式称为循环调制谱(cyclic modulation spectrum, CMS)，它通过评估滤波器组来输出平方包络的傅里叶变换从而跟踪频带内的周期性能量波动。可利用谱图的离散傅里叶变换(discrete Fourier transform, DFT)进行有效的CMS计算。描述为

(10)

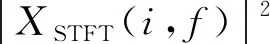
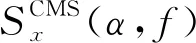
对应于式(8)，在第k个离散频率fk处，信号x的扫描光谱相关性通过式(11)获得。

(11)

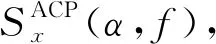
对应于STFT中的移位块R，其采样周期为R/Fs，则αmax表示为

αmax～Fs/2R

(12)

Q为最接近最大可观测循环频率αmax的频率索引

Q=[Fs/2RΔf]=[Nw/2R]

(13)

式中，[x]为通过四舍五入得到的整数，则快速循环相关谱通过式(14)定义

(14)

式中，Rw(α)为|w[n]|2的离散傅里叶变换。如式(9)一样，通过概率极限计算即可得到信号的循环频谱相关性信息。即

(15)

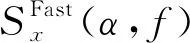
2 深度卷积神经网络

DCNN是深度学习中最常用的神经网络之一，由于具有多个隐藏层，在图像识别方面有着强大的学习能力。DCNN属于一种前馈神经网络，由一些过滤阶段和一个分类阶段构成。过滤阶段主要由卷积层、批量归一化层、激活层和合并层组成。分类阶段一般由几个全连接层和分类器组成。

2.1 卷积层

卷积层由一组需要参数学习的滤波器(卷积核)构成，每个滤波器都与对应的输入量相结合，通过加权平均的方法提取输入局部区域的函数，计算出神经元构成的激活图。然后将所有滤波器的激活映射按深度叠加得到输出，通过一系列的核权值和激活函数生成一个输出函数映射。在DCNN中广泛使用的线性整流函数(ReLU)被用作激活函数。卷积层的输出可以通过式(16)表示

(16)

式中：f为一个激活函数；k为卷积核；Mj为与输入对应的函数；l为网络层的顺序。

2.2 池化层

池化层通常放置在卷积层之后，以降低卷积特征映射的空间维数。通过对前一层生成的特征映射进行向下采样来实现空间不变性，输入图像被分成几个局部区域，并对每个区域执行池化函数来计算新值。常用的池化方法有平均池化、最大池化和规范池化。本文采用最大池化。在池化层l中，最大池化表示为

xl=down(xl-1,s)

(17)

式中：down(·)为最大池化层的下采样函数；xl为池化层的输出特征向量；xl-1为上一层的特征向量；s为池化大小。

2.3 全连接层

经过数个卷积层和池化层后，全链接层将二维特征映射的输出转换为一维向量，它将成为分类器的输入。其函数表达式为

h(x)=f(wx+b)

(18)

式中：x为输入特征向量；w为权重；b为偏执；f(·)为激活函数；h(x)为全连接层的输出。

2.4 分类器

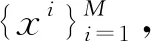
(19)

式中：θ=[θ1,θ2,...,θk]T为Softmax回归模型的参数向量；O为最终预测结果，所有预测结果之和为1。

3 基于循环相干谱和深度卷积神经网络的隔膜泵单向阀故障诊断

当隔膜泵单向阀工作在不同状态时，其仍然会保持组件的周期性运动，继而可能会激发结构的一个或多个固有频率。此外，在矿浆输送过程中，由于粗颗粒介质的存在，导致振动信号中产生异常冲击，并且其振幅也经常呈现随机波动。在这种情况下，传统的频谱分析方法通常不能在强噪声背景下揭示故障行为，尤其是在出现早期故障的情况下。因此，本文首先引入CSCoh作为数据的预处理步骤，通过对隔膜泵单向阀不同运行状态的循环平稳特性进行分析从而获得良好的特征表示。然后，利用快速循环相干谱生成的图片作为DCNN的输入；最后，通过设计的DCNN模型对隔膜泵单向阀进行故障诊断。所提出的隔膜泵单向阀故障诊断方法流程图如图1所示。具体实现步骤如下所述：

图1 CSCoh-DCNN方法的流程图

步骤1使用加速度传感器采集不同工作状态下隔膜泵单向阀的振动信号。并对每类信号按固定比率分段截取，然后将截取好的每段数据进行CSCoh变换生成新的样本集。

步骤2将样本集中的每个样本进行修剪和平滑处理为256×256尺寸大小的图片，这些图片将作为CNN的输入。

步骤3构建DCNN网络，对网络超参数进行初始化，如卷积核大小、偏置、全连接权值、迭代次数和学习率等；并选择交叉熵作为模型的损失函数。

步骤4用训练样本对DCNN模型进行训练，进而可将平滑处理过的CSCoh图逐层变换抽象以拾取各故障特征分布。

步骤5利用反向传播(back propagation, BP)算法以迭代方式来训练网络，并且使用自适应矩估计(adaptive moment estimation, Adam)优化器来加速模型训练，直至模型收敛。通过调整DCNN模型中卷积核权重以及各全连接层间权值以使实际预测不断收敛于期望输出，得到特征空间与状态空间的映射。

步骤6输出分类结果以提供全面的诊断分析。

4 工程实验验证

4.1 隔膜泵单向阀工作原理及实验平台

从结构上来看，隔膜泵的动力由电动机经过齿轮箱传递给三拐曲轴和连杆，使三拐曲轴的连续转动变为十字滑头的往复运动，从而带动活塞在活塞缸内做往复运动，进而带动隔膜做凹凸往复运动，使隔膜室内的压力发生变化，最终实现入料浆和排料浆的动作。当活塞向左时，带动隔膜做凸向动作，使隔膜室内的压力变小，进料单向阀打开而吸入矿浆；当活塞向右时，带动隔膜做凹向动作，使隔膜室内的压力变大，出料单向阀打开而排出矿浆。隔膜泵的简易结构图如图2(a)所示，加速度传感器安装位置及数据采集装置如图2(b)所示，表1为实验采集信号所用器件及其型号。本文中隔膜泵冲程数为30～31次/min，即运行频率为0.5～0.517 Hz，数据采样频率为2 560 Hz。

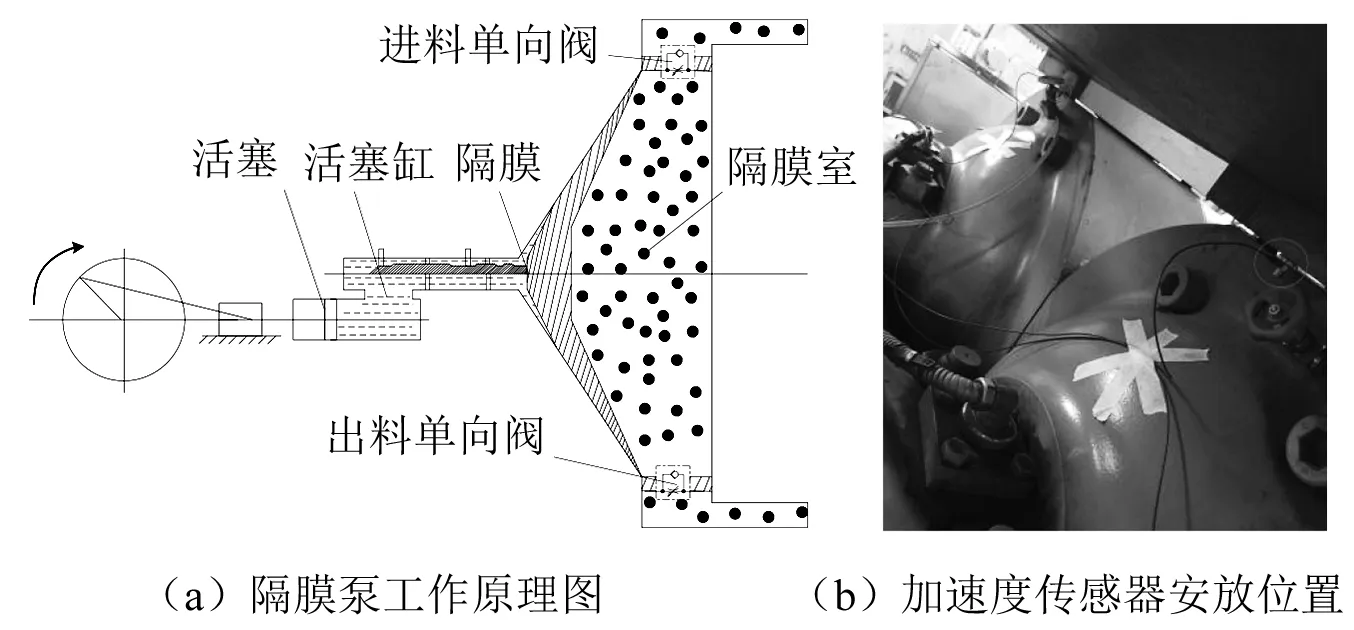
图2 隔膜泵工作原理图及加速度传感器安放位置

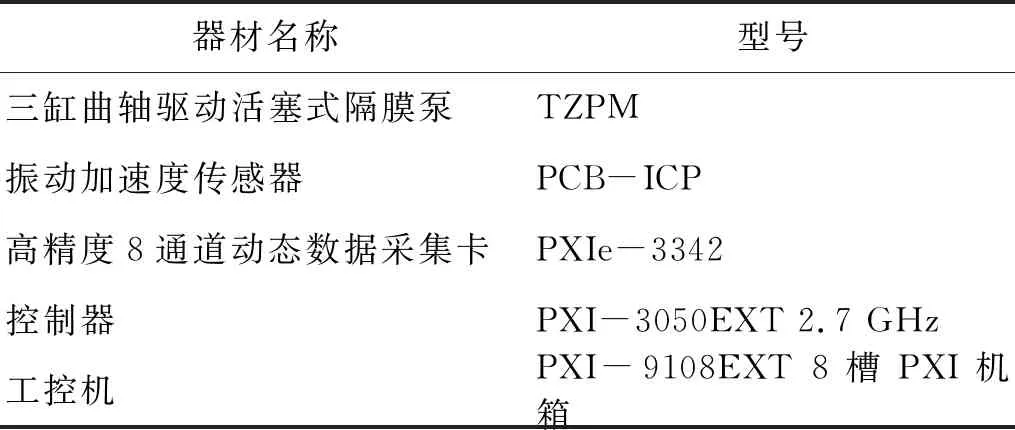
表1 数据采集器件和型号

4.2 单向阀振动信号特性分析

由于矿浆中固体颗粒的磨擦作用，泵组的进、出口单向阀工作一段时间之后势必将产生磨损。一旦进、出口单向阀产生损坏直至伤及阀室，导致浆体进入阀室将产生重大经济损失和安全隐患。因此，单向阀属于隔膜泵状态监测系统中重点监测对象。单向阀在隔膜泵系统中的安放位置及单向阀损坏故障图，如图3所示。

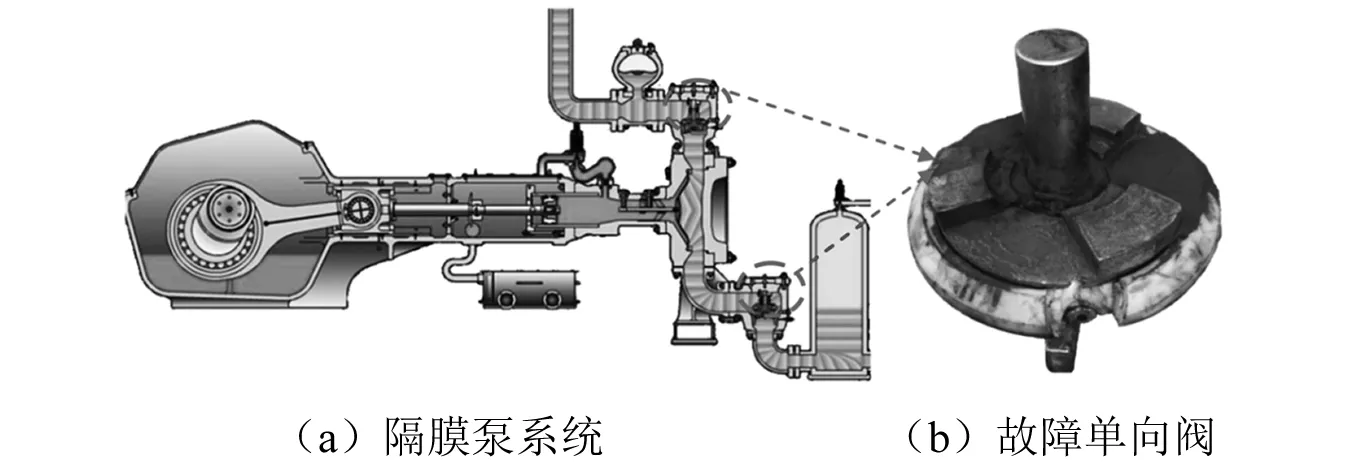
图3 隔膜泵系统及故障单向阀

隔膜泵单向阀数据集由4种类型组成，分别是正常数据(平稳的随机信号)；矿浆中存在的高硬度颗粒引起的划伤故障数据(时域中出现强脉冲)；输送介质持续冲击阀门密封面产生凹坑并引起泄露的磨损故障数据(信号中出现强噪声干扰)以及阀体击穿故障(清晰的周期性脉冲信号)。4种类型数据的时域信号如图4所示。

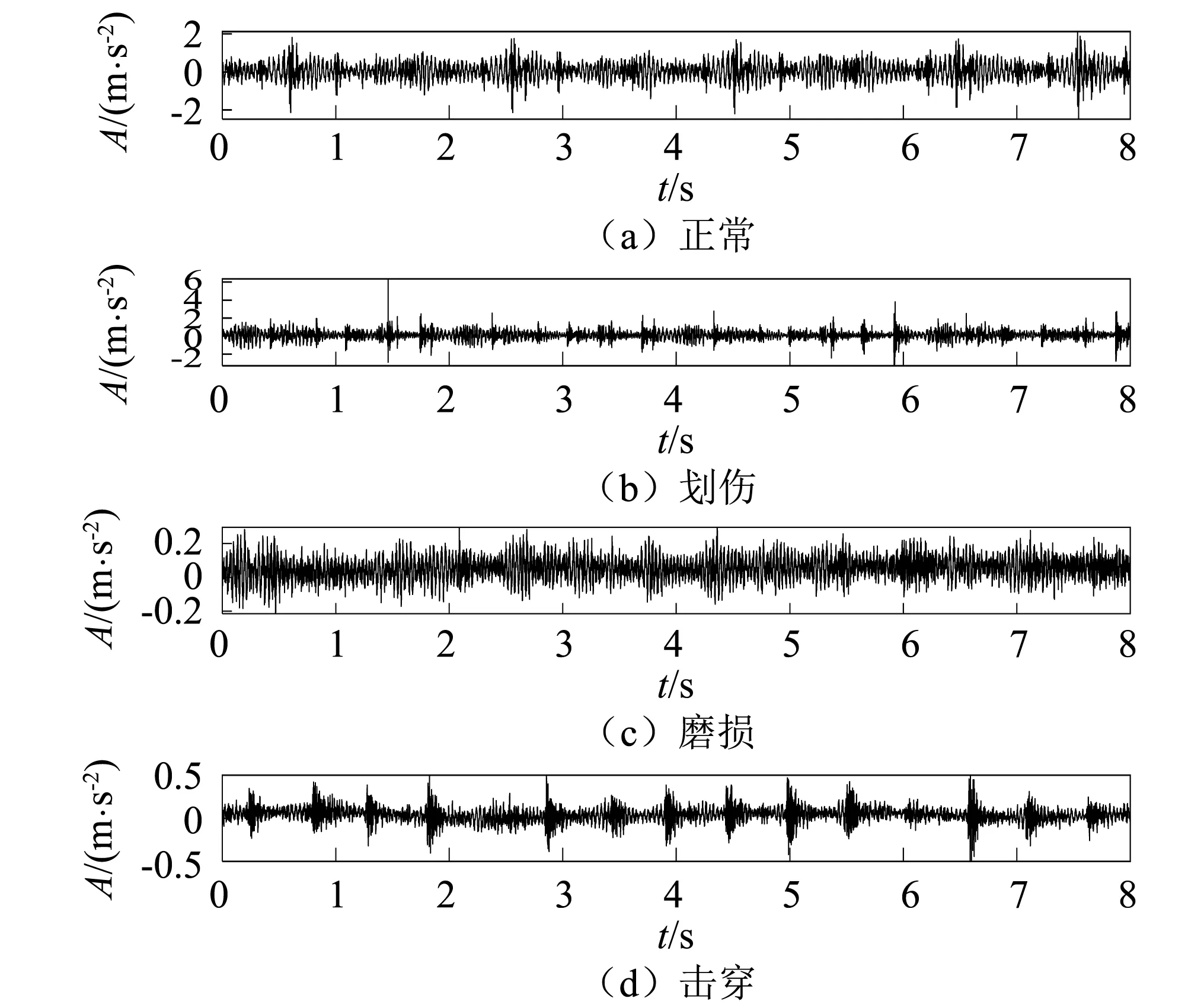
图4 单向阀不同工作状态下振动信号的时域波形图

同时，为研究CSCoh在揭示单向阀故障模式方面的有效性，分别在图5～图8中给出了不同健康状态下的CSCoh图以及对应的增强包络谱。可以观察到，CSCoh图为不同的故障类型提供了独特的特征信息。

在图5中，与平稳的随机信号特性相对应，CSCoh图和对应的增强包络谱中均表现为稳定的运行频率及其谐波；在划伤故障信号中，由于矿浆中坚硬粗颗粒的存在，破坏了原来的信号稳定性，信号变得无规则且存在强脉冲干扰，这在CSCoh图和对应的增强包络谱中均表现为杂乱的循环信息。在磨损故障中，通过图4(c)可知信号中存在强背景噪声的干扰，在时域中不能观察到有用信息，而在图7中则可以捕捉到击穿故障频率和高频干扰频率以及其对应的谐波信息，在CSCoh图中可以观察到对应光谱的存在(如椭圆虚线所示)，表明在磨损阶段，故障信息通常耦合于背景噪声之中，同时滋生出的高频干扰信息使信号变得更加复杂，常规手段难以检测到差异性特征；图8中CSCoh图和对应的增强包络谱中均可以清晰的观察到击穿故障频率以及谐波信息。综合可知，循环平稳性分析可以很好的反映隔膜泵单向阀不同故障类型的特征。

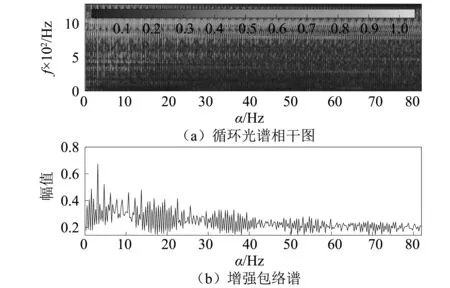
图5 正常信号的CSCoh图和对应的增强包络谱

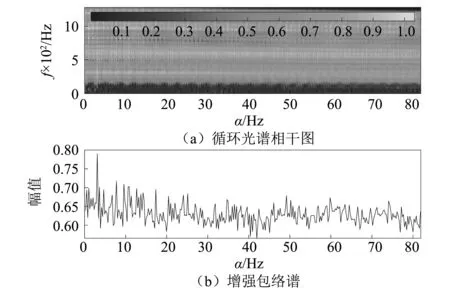
图6 划伤故障信号的CSCoh图和对应的增强包络谱

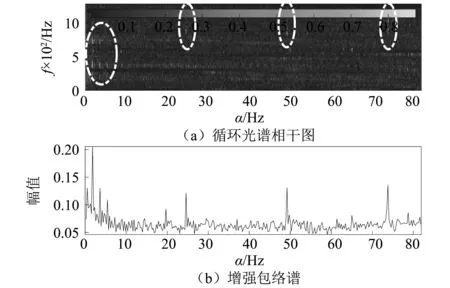
图7 磨损故障信号的CSCoh图和对应的增强包络谱

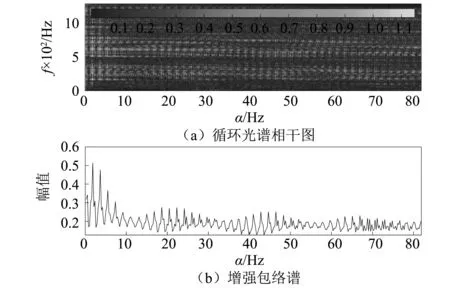
图8 击穿故障信号的CSCoh图和对应的增强包络谱

4.3 深度卷积神经网络设计

为实现隔膜泵单向阀的智能故障诊断，首先将收集到的诊断信号分为多个部分，在该实验中，4类数据通过无重叠截取10 240个数据点生成一个样本，然后将每个样本生成平滑和修剪处理后的CSCoh图，如图9所示，并将生成的图片作为DCNN的输入。共获得4×100个样本，按照8 ∶2的比例划分为训练样本集和测试样本集。

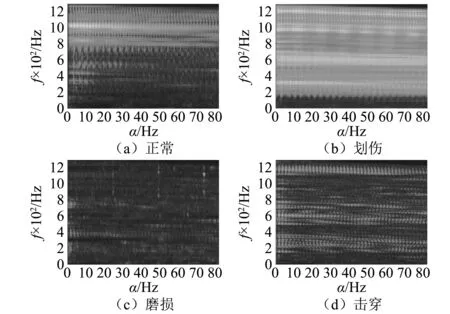
图9 不同健康状况平滑和修剪处理后的CSCoh图

为了有效实现对隔膜泵单向阀的精确诊断，必须构建合适的DCNN模型。考虑到复杂网络结构将导致计算过程更复杂，训练时间更长且易出现过拟合现象，所以充分利用前期研究成果以及实验条件，构建具有三层卷积层以及三层池化层模型结构，其激活函数选ReLu函数。在模型的全连接层部分，引入Dropout方法防止过拟合，并采用Softmax分类器对故障进行分类。具体模型参数如表2所示，其中：Conv1，Conv2，Conv3为卷积层；Pool，Pool2，Pool3为池化层；FC4，FC5为全连接层。

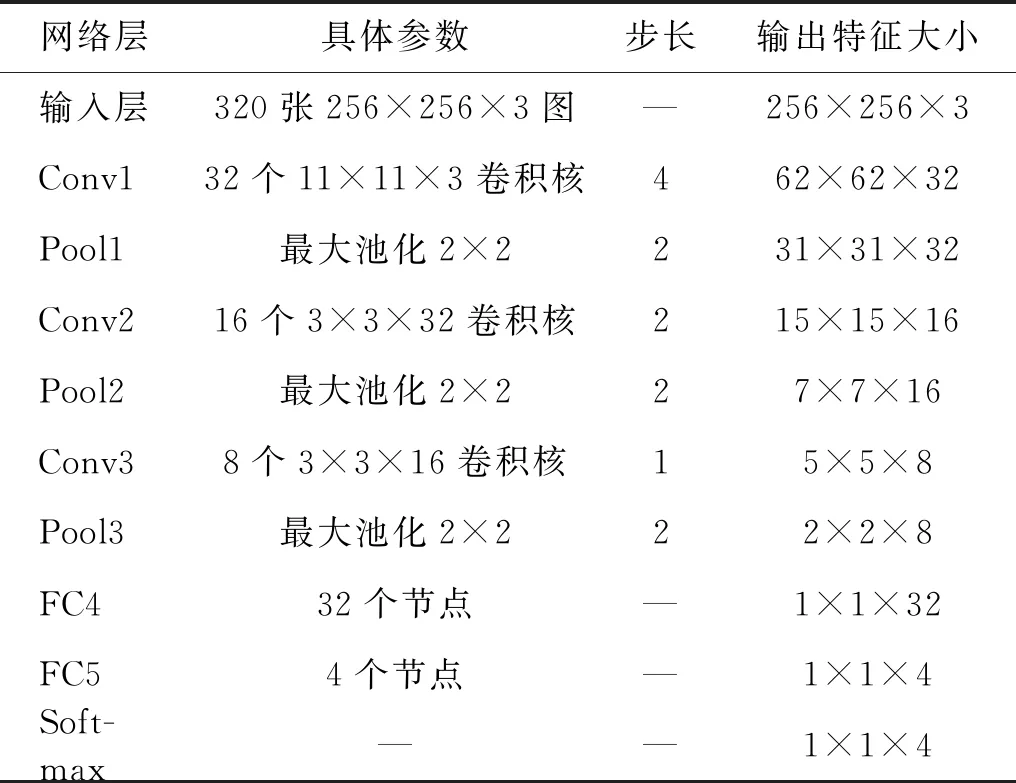
表2 DCNN模型具体参数

4.4 实验结果及分析

本文实验的环境配置：CPU为Intel@Core TMi7-8750H，GPU为Nvidia GeForce GTX1060，操作系统为ubuntu16.04，深度学习框架为Pytorch，软件平台为Matlab & Python。为了获取高精度的DCNN诊断模型，选择合适的超参数很重要，本实验基础学习率设置为0.001，训练以r=0.1，p=0.75进行迭代下降。MaxEpochs为30，采用Softmax分类器输出分类结果并最小化交叉熵损失函数。

训练过程如图10所示，其Accuracy曲线和Loss曲线反映了模型训练过程发生的变化，可以观察到随着迭代次数增加，模型诊断精度不断升高，误差不断下降并趋近于零。由图10可知当迭代数接近第20次时，DCNN模型达到了绝对收敛，训练平均总耗时107.31 s，对单张图片的平均分类时间约为0.018 s。

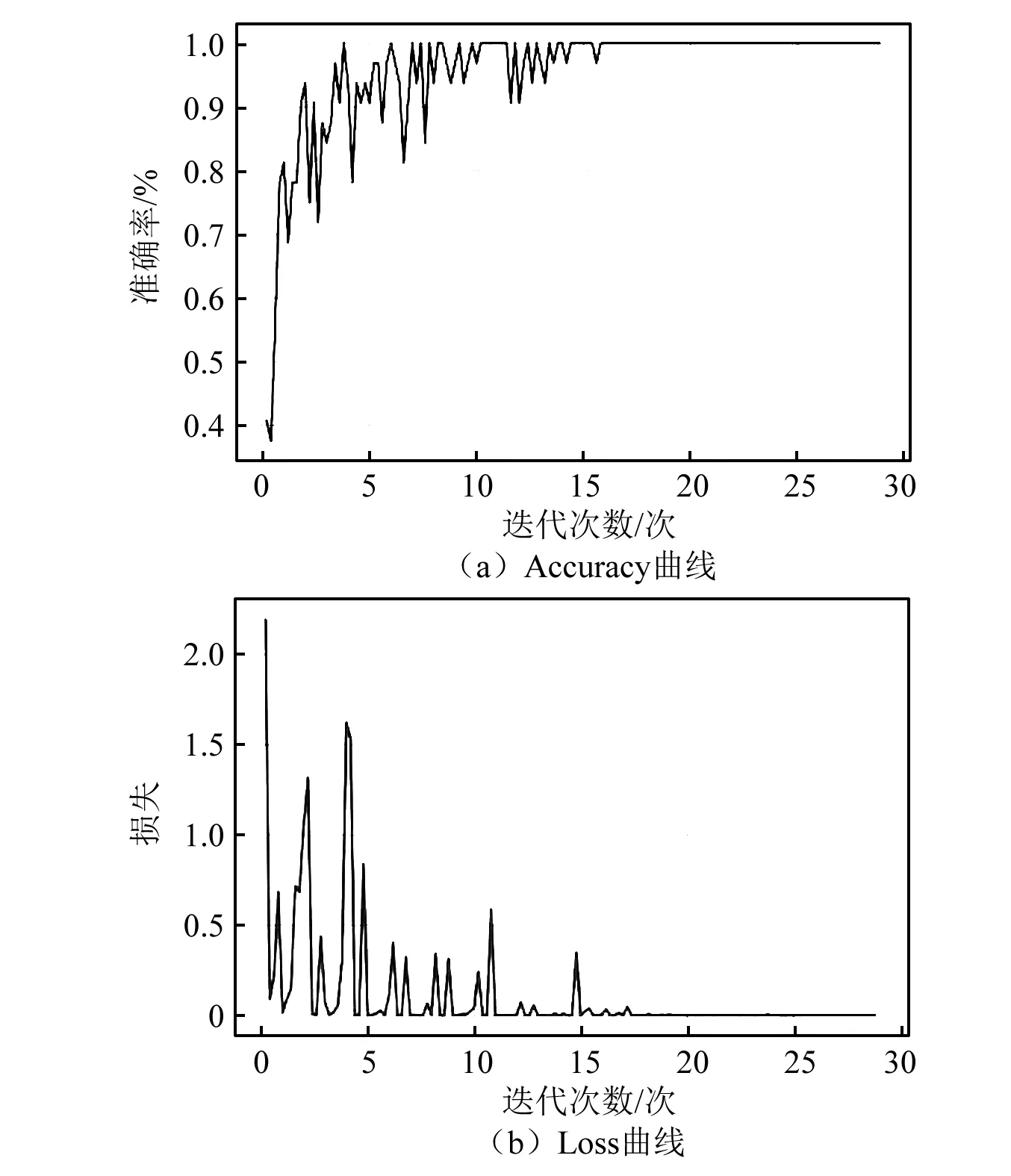
图10 训练结果曲线

为了清晰展现模型对每类故障的分类效果，本文采用混淆矩阵将测试集分类结果可视化。

如图11所示，可以观察到，模型对测试样本的分类准确率中，击穿故障准确率为95%，整体准确率达到了98.75%。可见，本文所构建的CSCoh+DCNN模型能完全识别不同类型的隔膜泵单向阀工作状态。同时，为了避免随机因素干扰，构建不同测试集进行10次实验，并采用F1分数(F1-Score)综合评价指标来表征模型的稳定性和泛化能力，每类故障的实验结果如图12所示。

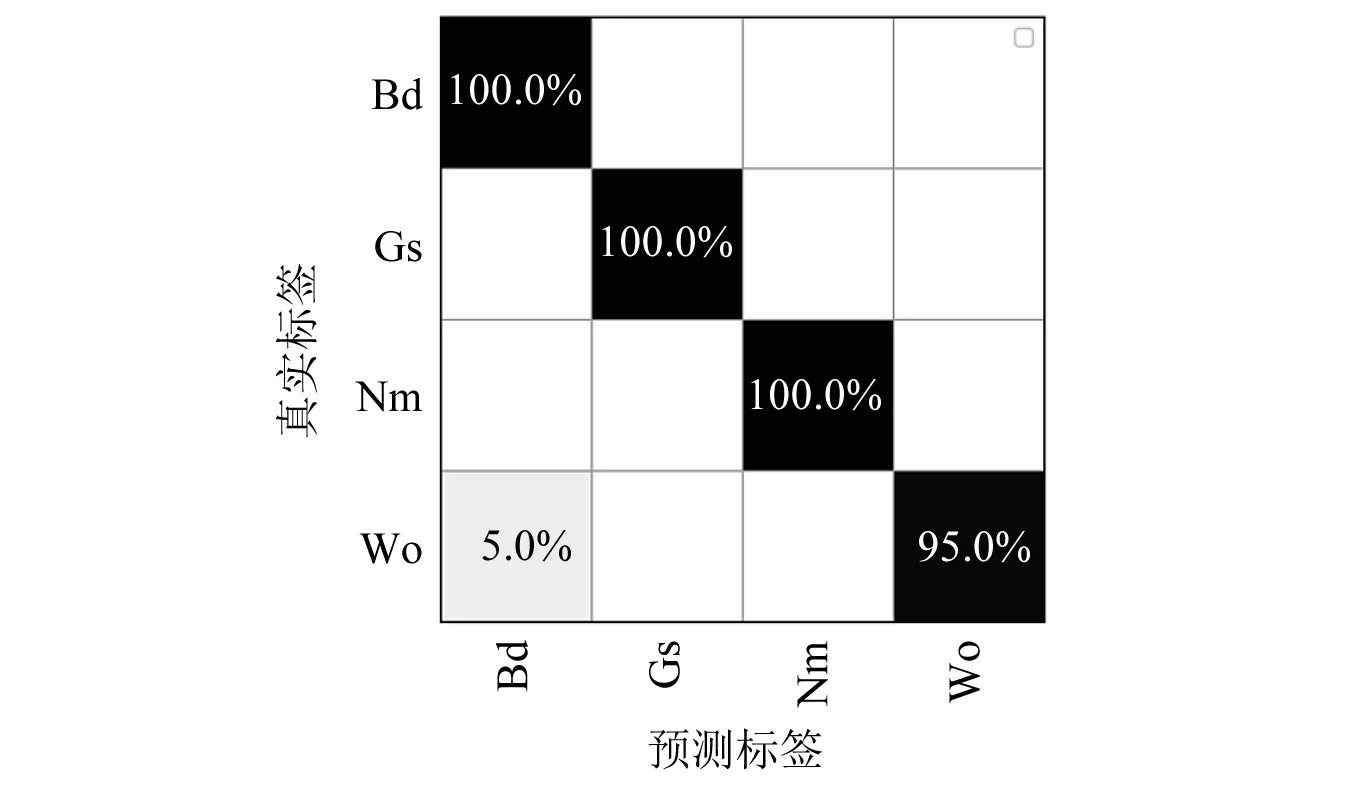
注：Bd为击穿； Gs为划伤； Nm为正常； Wo为磨损。

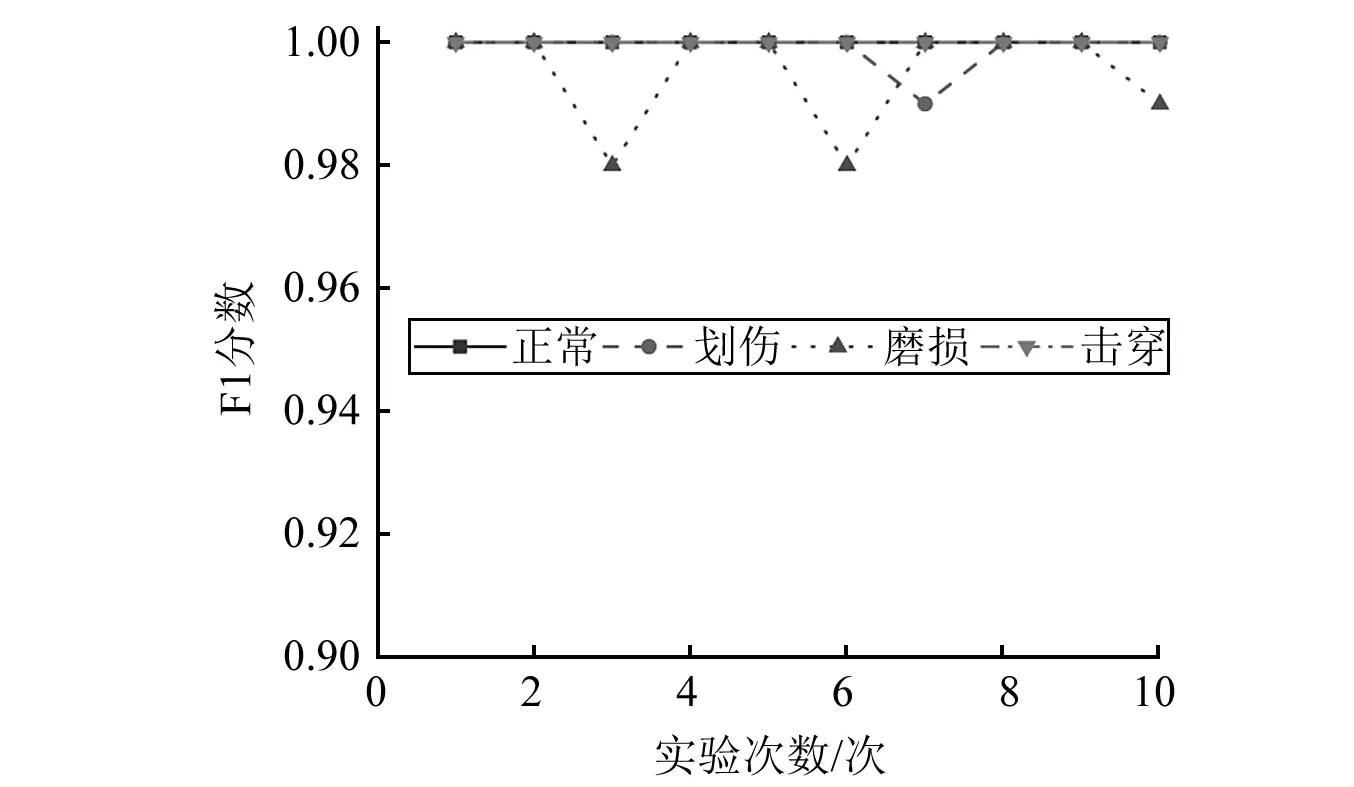
图12 10次实验F1分数评价

由于F1分数综合考虑了精确率和召回率两个指标，所以对模型分类性能具有更加客观的衡量。观察图12可知，本文所构建模型在10次实验中对正常和击穿2类故障均保持在100%的分类精度，其F1值均达到了1。而模型对划伤和磨损故障分类效果相当，其F1值在0.98～1.00。据此可知，本文所提方法确实对隔膜泵单向阀具有很好的分类性能，其稳定性以及泛化性能均表现优异。

同时，为说明本文所提方法相较于其他智能诊断方法的优势，将本文所提方法与Liu等的方法、Zhao等的方法、1D-CNN和STFT+DCNN等先进方法进行性能比较。同样为了避免随机因素干扰，上述实验均在不同测试集上进行10次，并统计其平均准确率以及标准差。实验结果如表3所示。

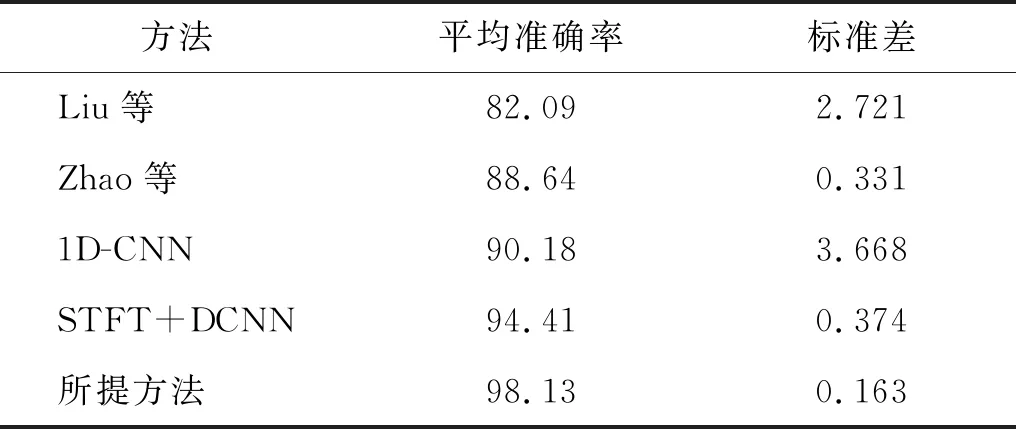
表3 10次实验诊断结果

通过分析表3可知，在与不同方法对比中，本文所提方法取得最好的分类效果，平均精确率达到98.13%。而Liu等和Zhao等采用常规特征+浅层分类器的方式，由于提取特征的方式未能捕捉到信号中的循环平稳分量，同时采用的是浅层学习的方式，使诊断性能仍然存处于较低的水平。1D-CNN和STFT+DCNN虽然采用了深度学习的方式，但由于信号中繁杂的干扰因素，使诊断精度和稳定性仍存在一定的局限性，其整体性能依然次于本文所提方法，验证了所提方法在隔膜泵单向阀故障诊断中的卓越性能。

5 结 论

隔膜泵单向阀在实际工况环境下运行时，通常伴随着复杂的背景噪声和强烈的异常冲击，这导致故障诊断中存在难以设计有效的特征指标和诊断性能有限的问题。基于此，本文设计了一种将CSCoh和DCNN相结合的隔膜泵单向阀故障诊断方法，与传统的人工智能方法相比，基于DCNN的故障诊断模型在特征提取和分类方面具有强大的功能。同时，考虑到DCNN的性能会受到数据集的规模和质量的影响，将CSCoh用于揭示不同类故障性质的预处理步骤，通过领域知识与信号处理技术的有机结合大大减轻了网络的学习难度。通过与其他机器学习方法和1D-CNN、STFT+DCNN等深度学习方法对比，验证了所提方法的优越性。