含噪多频信号频率估计算法

陈 鹏， 刘春华， 苏 欣， 涂亚庆， 赵少美

(1. 中国空气动力研究与发展中心 空气动力学国家重点实验室，四川 绵阳 621000；2. 中国空气动力研究与发展中心 设备设计及测试技术研究所，四川 绵阳 621000；3. 陆军勤务学院 军事物流系，重庆 401311)

多频信号可理解为多个单频信号的叠加，其频率估计广泛应用于线性系统识别、低频机械光谱学、电力系统、核磁共振波谱分析以及无损检测等诸多领域[1-3]。

目前，针对多频信号的频率估计算法大致可分为两大类：时域法和频域法。时域法如线性预测法(linear prediction, LP)[4]、计算量更加复杂的多重信号分类法(multiple signal classification, MUSIC)[5]、旋转不变估计法(estimating signal parameter via rotational invariance techniques, ESPRIT)[6]。时域法分辨率高，但所需采样序列长，导致计算量大，且抗噪性差，不利于实际应用。频域法主要利用离散傅里叶变换法(discrete Fourier transform，DFT)对信号进行频谱分析，可利用DSP(digital signal processing)和FPGA(field programmable gate array)等硬件直接实现、计算速度快，抗噪性好，是研究多频信号频率估计的主要方向[7]。

单频信号是多频信号的一种特例，也是研究重点。文献[8]通过频谱两点插值和迭代计算，实现了频率高精度估计，后续称为AM法。文献[9]利用频谱三点插值得到频率估计值，后续称为Candan法。针对单频信号，AM法和Candan法分别是迭代类算法和非迭代类算法中综合性能最好的算法，但处理多频信号时，二者均受其他非待估计频率分量频谱泄漏的影响，频率估计精度差，不能直接使用。

为抑制频谱泄漏影响，文献[10-11]在AM法的基础上，采用频谱相减策略实现了频谱泄漏校正，提高了频率估计精度，但在信号频率间隔较近和中高信噪比条件下的频率估计精度有待提高。

文献[12]首先用改进的AM法求取多频信号各频率分量的频率粗估计值，然后构造信号中非待估计的所有频率分量，并通过相减策略以抑制频谱泄漏的影响，与Ye等研究中的YA法具有相当的估计性能。但该算法减去非待估计频率分量这一步骤只进行了一次，导致频率估计精度受频率粗估计值的影响。特别是在信号频率间隔较近、频谱粗估计存在较大偏差时，由于信号中的非待估计频率分量减去不彻底，使得算法仍受频谱泄漏的影响，降低了频率估计精度。

Djukanovi[13]通过滤除信号中非待估计频率分量的方式来提高频率估计精度，针对单频实信号，提出了DFE-1法。首先利用Candan法对信号进行预处理，得到频率粗估计值，并生成参考信号；然后将信号与参考信号相乘以实现频率搬移，通过滤除直流分量的形式降低频谱泄漏的影响；最后采用AM法对滤除了非待估计频率分量的信号进行迭代计算，提高了信号频率估计精度。针对多频信号，在DFE-1法的基础上进行了推广，提出了DFE-2法，实现了多频信号频率的高精度估计[14]。

DFE法对提高多频信号的频率估计精度提供了思路，但存在设计缺陷，影响了频率估计精度。本文在分析频谱泄漏影响和DFE法缺陷的基础上，提出了新的频率估计算法，并通过仿真实验验证了所提算法的有效性。

1 问题描述

根据信号参数是否随时间变化，采样信号可分为平稳信号和非平稳信号，本文以平稳信号为模型进行分析。不失一般性，具有M个频率分量的平稳多频信号如式(1)所示。

(1)

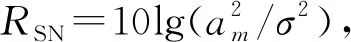
特别说明：频率分量个数M可以是已知的，也可以是未知的。在实际应用中，M一般是未知的，可通过广义阿卡克信息准则和最小长度描述法等方式计算得到。对频率分量个数M进行估计属于信号检测范畴，不属于信号参数估计领域，是一个独立的问题。本文直接利用已有算法得到信号频率分量个数，然后将M作为先验知识进行处理，后续不再对其进行讨论。

特别地，当M=2，且ω1=-ω2，a1=a2，θ1=θ2时，采样信号称为单频实信号。

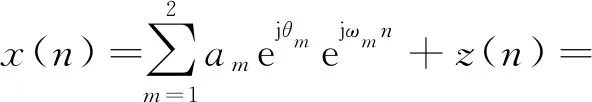
(2)

单频实信号是一种特殊的多频信号，含有正频率分量和负频率分量。设计多频信号频率估计算法时，对单频实信号的频率估计进行讨论，是有必要且具有代表性的。

在对多频信号进行频谱分析时，可将其频率表示为

(3)

式中：km=[ωmN/2π]为第m分量在频谱中能量最大值点的索引； [·]为取最接近于·的整数；-0.5≤δm≤0.5为第m分量的频谱偏移量。因此，要得到精确的频率估计值，需要得到准确的频谱索引和精确的频谱偏移量。

在对信号第m分量进行频率估计时，频率估计精度受其他频率分量频谱泄漏和噪声的叠加影响。由于DFT法具有很强的抗噪性，噪声的影响相对较小。为直观理解频谱泄漏的影响，在无噪条件下，对多频信号和单频信号进行频谱分析，如图1所示。

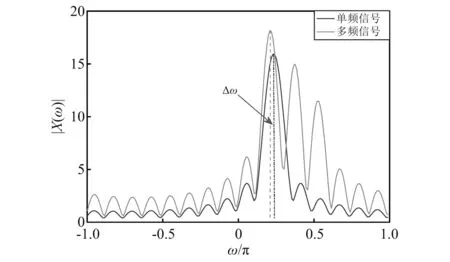
图1 单频信号和多频信号频谱

可以看出，受其他频率分量频谱泄漏的叠加影响，多频信号待估计频率分量的频谱值大于同频单频信号的频谱值，从而影响由频谱分析得到的频率估计值，与真实的频率值存在估计偏差。

2 DFE算法

针对单频实信号，Djukanovic提出了DFE-1算法，流程如表1所示。

表1 DFE-1算法流程

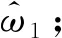
在此基础上，Djukanovic提出了针对多频信号的频率估计算法，后续称为DFE-2法。与DFT-1法相比较，两个算法的流程一致。DFE-2法沿用了DFE-1法滤除信号中非待估计频率分量的思路，但在进行频率粗估计和精估计时，均结合了Candan法和三点周期图最大化法，没再使用AM法。

DFE法抑制了非待估计频率分量频谱泄漏的影响，但存在设计缺陷：

(1) DFE-1法分别利用非迭代类Candan法和迭代类AM法对单频实信号进行频率粗估计和精估计，但将粗估计和精估计两个步骤完全分开，既增加了计算量也降低了频率估计精度。特别是在信号频率较低，即信号正频率和负频率相隔很近、频谱泄漏严重时，容易导致负频率分量滤除不彻底，使得频率估计精度受频率粗估计的影响更加严重。

(2) 相位是关于频率的函数，但DFE-1法在进行频率搬移时，只考虑了信号频率，没有考虑相位，降低了频率估计精度。

(3) 针对多频信号，DFE-2法分别进行了一次频率粗估计和频率精估计，可以理解为进行了迭代计算。但在处理滤除了非待估计频率分量的单频信号时，选用了非迭代类Candan法和三点周期图最大化法，导致频率估计精度受频率粗估计的影响，且三点周期图最大化法计算更加复杂，增加了计算量，降低了算法实时性。

(4) DFE-2法也没有考虑相位的影响。

3 所提算法

为提高多频信号的频率估计精度，利用DFE法的思路，提出了新的参数估计算法，详细步骤如下：

步骤1对采样信号进行FFT计算，并求信号频谱中最大的M个极大值。

(4)

(5)

式中：f(·)为求函数·中最大M个极大值的索引；ki为第i分量的索引，i根据各频率分量频谱最大值递减的顺序依次排列，即k1和kM分别为信号频谱M个极大值中最大值和最小值的索引。

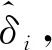
(6)

(7)

式中，|·|和∠·分别为取复数·的模和角度。

步骤3对信号进行频率搬移，滤除信号中的其他非待估计频率分量。

分析时，按照信号频谱能量最大到最小的顺序进行分析，即从k1依次分析到kM。

首先构造其他非待估计频率分量的参考信号

(8)

式中，m根据非待估计分量频谱最大值递减的顺序依次排列。

其次将参考信号与多频信号相乘，将非待估计中的第m分量(m=1)搬移到0频附近，得到搬移信号。

ym(n)=x(n)rm(n)

(9)

然后将搬移信号中0频附近的信号能量视为直流分量，利用式(10)滤除直流分量，并将信号搬移回原频率处，得到抑制了第m分量的降频信号。

(10)

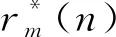
最后将降频信号xM-1(n)代入式(9)和式(10)，滤除非待估计频率分量中的第m分量(m=2)，得到降频信号xM-2(n)。按照m的取值顺序，重复式(9)、式(10)，依次滤除信号中非待估计频率分量，最终得到只含有第i分量的降频信号x1(n)。

步骤4采用AM法对降频信号x1(n)进行分析，在索引ki两边插值，间隔为0.5。利用式(11)计算插值点的频谱值，并根据两个插值点的频谱由式(12)计算频谱偏移量。

(11)

(12)

步骤5按照i的取值顺序，循环计算步骤2～步骤4，得到每个频率分量的参数粗估计值。

步骤6迭代计算步骤2～步骤5，进一步提高各频率分量的参数估计精度，得到各频率分量的幅值和初相位估计值，并利用式(3)得到各频率分量的频率估计值。

综上分析，算法的具体流程如表2所示。

表2 算法流程

此外，针对单频实信号，根据表2的算法流程，即可得到滤除了负频率分量频谱泄漏影响的频率估计值。

与DFE法的不同处在于：

(1) 不单独区分信号频率粗估计和精估计，均在迭代中进行计算，既可以更加有效地滤除非待估计频率分量的影响，提高频率估计精度，也可以降低计算量，提升算法实时性。

(2) 滤除非待估计频率分量时，考虑了相位的影响，有利于更加彻底地滤除非待估计频率分量，从而提高频率估计精度。

所提算法和DFE法、以及其他现有优秀算法的性能将在仿真验证中进行对比分析，检验所提算法的优越性。

4 仿真验证

为检验所提算法的有效性，利用MATLAB软件在不同条件下，对多频信号和单频实信号进行频率估计，且主要对多频信号进行分析。为降低计算时的随机误差，每组仿真进行2 000次蒙特卡罗实验。为方便分析，将估计结果转换为均方误差(mean square errors, MSEs)，并用对数表示。

(13)

式中，L式蒙特卡罗实验次数。

实验时，以含有3个频率分量的信号为例进行频率估计，并与YA法、AK法、DFE-1法、DFE-2法、Ye法[15]以及克拉美罗下限(Cramer-Rao lower bound，CRLB)[16]进行对比分析。设采样信号x(n)=1.5ej(3.1ωsn+θ1)+1.4ej((4.7+Δk)ωsn+θ2)+1.2ej((8.3+Δk)ωsn+θ3)+z(n)，长度为128，索引间隔Δk以1为步长从1增加到32，初相位θ1，θ2和θ3独立随机取值。

(1) 不同迭代次数

所提算法属于迭代类算法，首先分析算法在不同迭代次数下的频率估计性能。仿真时，设SNR为30 dB，迭代次数为1，2，3和4，结果如图2所示。

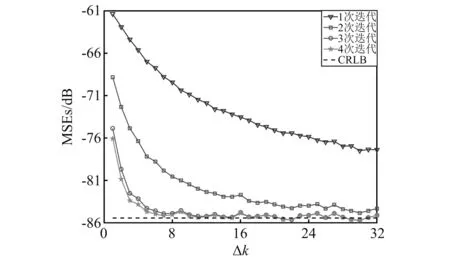
图2 不同迭代次数的频率估计结果

经由1次或2次迭代时，算法整体估计效果较差，但随着频率间隔增大而逐渐变好，且2次迭代的频率估计精度高于1次迭代的频率估计精度。当频率间隔较大(Δk≥5)时，3次和4次迭代具有相当的估计性能，信号各频率分量频谱间相互泄漏对所提算法的频率估计精度影响非常小，频率估计结果靠近CRLB。当频率间隔相距非常近时，4次迭代效果更好，考虑到算法的估计精度，特别是在信号频率相隔较近、频谱泄漏严重时频率估计精度，后续实验均采用4次迭代计算。

(2) 无噪声

由前文分析可知，利用频域法对多频信号进行频率估计时，受频谱泄漏和噪声的影响。因此，在无噪声环境下，可以检验各算法对频谱泄漏的抑制能力，仿真结果如图3所示。

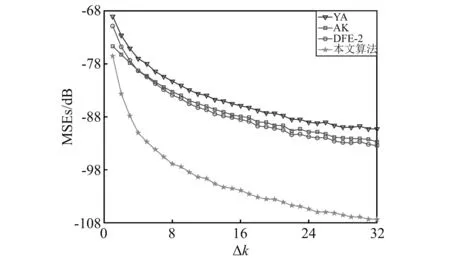
图3 无噪声条件下的频率估计结果

在不同频谱泄漏程度下，AK法的频率估计精度优于YA法。当频率相隔较近、频谱泄漏严重时，AK法优于DFE-2法；当频率间的间隔较大、频谱泄漏影响减小时，DFE-2法的效果优于AK法。相比其他算法，本文算法采用频率搬移策略滤除了信号中其他非待估计频率分量，抑制了多频信号中其他频率频谱间的泄漏影响，具有更强的频谱泄漏抑制能力，明显强于其他几种算法，达到了算法的设计目的。

(3) 不同信噪比a

为说明算法在不同信噪比下的估计性能，设x(n)=1.5ej(3.1ωsn+θ1)+1.35ej(7.2ωsn+θ2)+1.2ej(10.3ωsn+θ3)+z(n)，在SNR以1 dB为步长从0增加到30 dB的条件下进行了仿真实验，结果如图4所示。

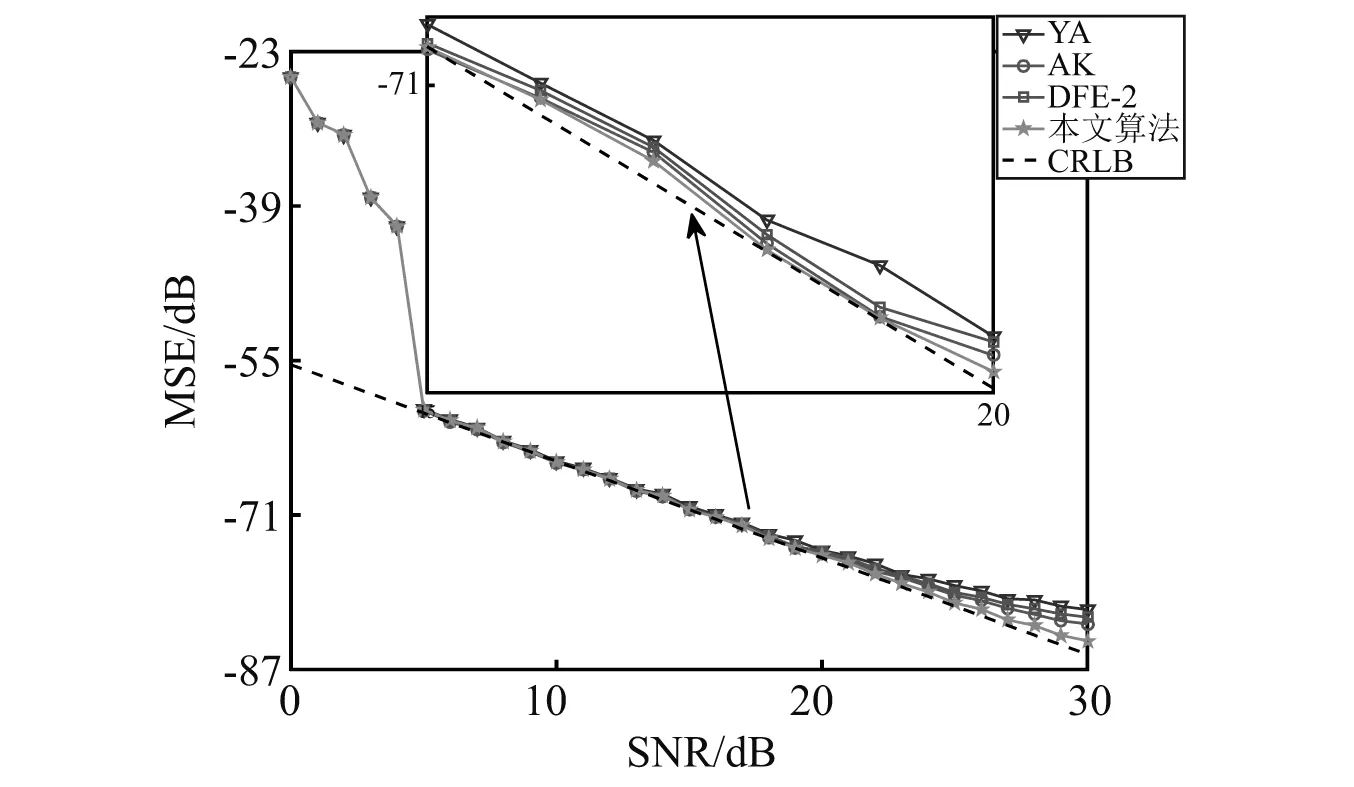
图4 不同信噪比条件下的多频信号频率估计结果

当信号频率间隔小且各频率分量的能量大小相近时，算法受噪声影响大，在SNR<5 dB时的频率估计精度很差。在5 dB15 dB、即频率估计精度受频谱泄漏影响更严重时，各算法均出现了频率估计偏差，逐渐偏离CRLB，但相比于YA法、AK法和DFE-2法，本文算法的频谱泄漏抑制能力更强，频率估计精度最高，最接近CRLB，优于其他几种算法。

(4) 不同信噪比b

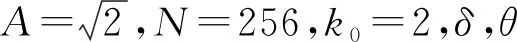
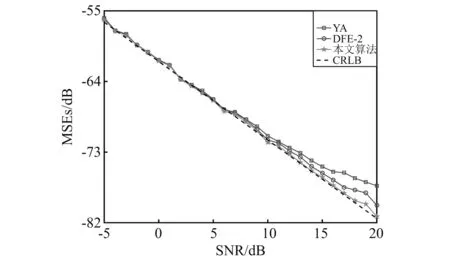
图5 不同信噪比条件下的单频信号频率估计结果

当信号频率较低，即信号正频率和负频率分量相隔较近、频谱泄漏严重时，本文算法优势明显。当SNR<5 dB时，Ye法、DFE-1法和本文算法具有相当的估计精度，均靠近CRLB。当SNR>5 dB时，Ye法和DFE-1法的估计精度逐渐降低、逐渐偏离CRLB，且DFE-1法优于Ye法。当-5 dB

5 结 论

本文算法通过信号预处理、构造参考信号、频率搬移、滤除非待估计频率分量等方式抑制了多频信号中非待估计频率分量频谱泄漏的影响，并经迭代计算得到了各频率分量精确的频率、幅值和初相位估计值。

仿真实验结果表明，所提算法有效地抑制了多频信号中频谱泄漏的影响，具有更高的频率估计精度，频率估计值的均方误差比DFE法和其他现有优秀算法的频率估计结果更靠近CRLB。