精密机床角接触球轴承打滑特性仿真分析

许世钰，李伦，李济顺，牛宝禛，金喜洋

(1.河南科技大学 机电工程学院,河南 洛阳 471003；2.河南省机械设计及传动系统重点实验室,河南 洛阳 471003)

角接触球轴承是精密机床的核心部件，其运动状态将直接影响精密机床的加工精度和运转性能。在高速工况下，球会打滑，保持架运转不稳定，轴承各零件之间会发生摩擦磨损和剧烈碰撞，这不但会影响机床主轴的精度和性能，更会导致轴承过早失效，故有必要对精密机床主轴轴承打滑特性进行分析。

国内外学者对滚动轴承打滑做了大量研究：文献[1]基于弹流润滑理论提出一种可以预测保持架角速度的方法，并通过保持架角速度的变化来预测滚动体打滑；文献[2]建立角接触球轴承打滑动力学模型，分析了角接触球轴承在不同工况下的打滑特性，结果表明适当的轴向载荷可以避免严重的打滑；文献[3]建立了在径向载荷下滚动轴承进入载荷区时的打滑动力学模型，分析了滚动体由无载区进入承载区时的打滑特性；文献[4]建立了考虑保持架动态不平衡的动力学分析模型，分析了动态不平衡量对圆柱滚子轴承保持架打滑特性的影响；文献[5]考虑径向游隙、滚子凸度等因素建立了圆柱滚子轴承打滑动力学模型，研究结果表明增大径向载荷、弯矩或时变载荷幅值可减小滚子的打滑；文献[6]建立了滚动体打滑非线性动力学模型，考虑径向游隙、保持架兜孔间隙等因素，分析了不同工况下的滚动体打滑，结果表明转速增大会导致承载区滚动体打滑速度增加，载荷增大会缩小滚动体打滑范围；文献[7]建立了减速工况下的圆柱滚子轴承动力学模型，分析了不同工况下结构参数对圆柱滚子轴承减速阶段打滑特性的影响，并通过试验对稳定工况下的打滑特性进行验证；文献[8]在考虑油气阻力和滚子与保持架的摩擦力基础上，推导出能够更好分析高速圆柱滚子轴承打滑的拟动力学模型；文献[9]建立了考虑沟道波纹度的深沟球轴承动力学分析模型，分析了表面波纹度波数及最大幅值对保持架打滑率的影响；文献[10]基于欧拉方程建立角接触球轴承打滑动力学模型，分析了在轴向和径向载荷联合作用下球滑动速度的变化规律；文献[11]以FAG-B71956E 角接触球轴承为研究对象，通过试验得到该球轴承的打滑临界曲线。

国内外学者对轴承打滑特性的研究主要集中在通过建立动力学模型进行理论分析，在仿真分析方面的研究较少，已有的仿真分析大多假设轴承为全刚体。鉴于此，以H7006C角接触球轴承为研究对象，考虑油膜对轴承接触刚度的影响，基于ANSYS对轴承内外圈及保持架进行柔性化处理，并采用ADAMS多体动力学软件建立角接触球轴承刚柔耦合动力学模型，分析内圈转速、径向载荷和轴向载荷对角接触球轴承打滑特性的影响。

1 角接触球轴承刚柔耦合多体动力学模型

H7006C角接触球轴承主要结构参数见表1，内外圈材料为GGr15Z轴承钢，球材料为Si3N4陶瓷，保持架材料为聚酰亚胺，材料参数见表2。润滑采用4106航空润滑油，动力黏度为0.055 Pa·s，黏压指数为1.85×10-8Pa-1。

表1 H7006C角接触球轴承主要结构参数Tab.1 Main structural parameters of H7006C angular contact ball bearing

表2 H7006C角接触球轴承材料参数Tab.2 Material parameters of H7006C angular contact ball bearing

1.1 刚柔耦合模型

基于Solidworks建立H7006C角接触球轴承三维模型，转换为Parasolid格式后导入ADAMS中进行仿真分析。ADAMS仿真默认进行全刚体动力学分析，无法准确计算运动过程中球与内外圈的弹性变形，且轴承零件之间的相对运动主要依靠接触力传递，将内外圈和保持架作为刚体无法准确模拟球与保持架的运动状态。鉴于此，基于ANSYS分别对角接触球轴承内外圈和保持架进行柔性化处理，导出MNF文件，并在ADAMS中替换刚性内外圈和保持架，建立刚柔耦合多体动力学模型，如图1所示。

图1 H7006C角接触球轴承刚柔耦合模型Fig.1 Rigid-flexible coupling model of H7006C angular contact ball bearing

1.2 施加约束与载荷

限制外圈6个方向的自由度，保留内圈绕轴线方向的旋转、轴向和径向平移3个自由度，保留球和保持架6个方向的自由度。

在内圈上施加沿轴线方向的轴向力及沿重力方向的径向力，并施加绕其轴线方向的转速。保持架和内、外圈与球之间建立Impact函数接触副，球数为18，需建立54组接触对。

1.3 接触参数的设定

基于赫兹接触理论，将2个碰撞体之间考虑为非线性弹簧阻尼器模型，用冲击函数法计算球与内、外圈和保持架之间的接触力，impact接触力函数表达式为

(1)

式中：Fimpact为法向接触压力；q为两接触体发生碰撞后的实际距离；q0为两接触体之间的初始距离；K为等效接触刚度；e为法向接触压力指数，对于点接触，e取1.5；cmax为最大阻尼系数，一般取等效接触刚度的0.1%～1%[12]；dq/dt为两接触体之间的相对速度；d为法向穿透深度，最大阻尼系数和法向穿透深度的关系如图2所示，其取值决定最大阻尼系数，考虑到仿真收敛性，d取0.1 mm；step为阶跃函数。

ADAMS软件采用Coulomb模型计算接触体之间的摩擦力，摩擦因数为

图2 最大阻尼系数与穿透深度的关系Fig.2 Relationship between maximum damping coefficient and penetration depth

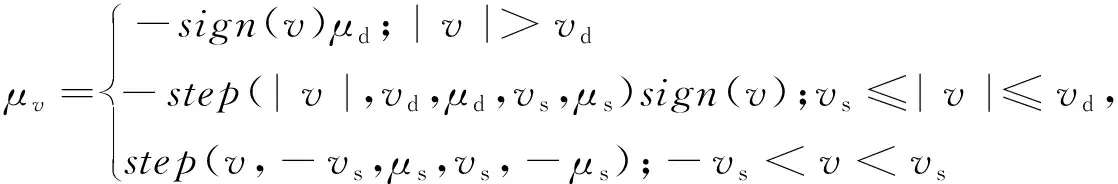
(2)

式中：sign为符号函数，影响动摩擦因数取值的正负；v为两接触体之间的相对滑移速度；μd为两接触体的动摩擦因数；vd为动态滑移速度；μs为两接触体的静摩擦因数；vs为静态滑移速度。

文中定义vs=100 mm/s，μs= 0.1，vd=1 000 mm/s，μd=0.02[13]。

2 角接触球轴承等效接触刚度计算

转速和载荷的变化会引起轴承接触刚度的变化，接触刚度的变化会使轴承接触特性变化，进而影响轴承打滑特性。

角接触球轴承在高速运转时，球与内、外圈之间会存在弹流动力润滑。基于赫兹接触理论计算的接触力忽略了油膜对球与沟道之间的接触弹性变形的影响。考虑弹流润滑作用，球与沟道的等效接触刚度可简化为球与内(外)圈的接触刚度Ki(e)和弹流润滑油膜刚度K0的串联。

图3 弹流润滑接触模型Fig.3 Contact model of elastohydrodynamic lubrication

2.1 赫兹接触刚度

根据赫兹接触理论，球与内、外圈的接触刚度Ki和Ke可表示为

(3)

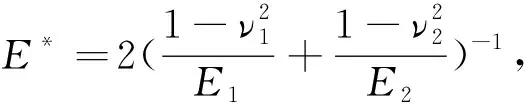
(4)

式中：E*为综合弹性模量；E1，E2分别为套圈和球材料的弹性模量；ν1，ν2分别为套圈和球材料的泊松比；ρi，ρe分别为球与内、外圈接触点的主曲率；ndi和nde为接触变形系数。

2.2 油膜刚度

由弹流动力润滑理论可知，轴承最小油膜厚度决定油膜刚度，油膜刚度可近似由载荷对最小油膜厚度求导得到。在等温且供油充足的情况下，球与内、外圈之间的最小油膜厚度为[14]

hmin=3.63U0.68G0.49W-0.073(1-e-0.68k)Rx，

(5)

U=vmη0/(E*Rx)，

G=α1E*，

k=1.039 9(Ry/Rx)0.636，

式中：vm为轴承平均速度；η0为常压下润滑油的动力黏度；Rx，Ry分别为球在x，y方向的当量半径；α1为润滑油黏压指数；Q为法向接触载荷；k为接触椭圆率。

球与内、外圈之间的油膜刚度K0为

(6)

2.3 等效接触刚度

球与内、外圈的等效接触刚度为

(7)

转速和轴向载荷对轴承等效接触刚度的影响分别如图4和图5所示：1)随转速增大，球与内、外圈的等效接触刚度减小；2)随轴向载荷增大，球与内、外圈的等效接触刚度增大。

图4 转速对H7006C轴承等效接触刚度的影响Fig.4 Effect of rotational speed on equivalent contact stiffness of H7006C bearing

图5 轴向载荷对H7006C轴承等效接触刚度的影响Fig.5 Effect of axial load on equivalent contact stiffness of H7006C bearing

3 角接触球轴承打滑仿真分析

角接触球轴承高速运转时，在离心力和陀螺力矩的作用下球的运动状态复杂，不易检测，而保持架依靠球与其之间的碰撞力围绕轴线公转，可将保持架打滑率作为衡量球打滑程度的重要指标。保持架打滑率为

S=(1-ωbs/ωb)×100%，

(8)

ωb=ω(1-Yi)cos(αe-β)/[(1+Ye)·

cos(αi-β)+(1+Yi)cos(αe-β)]

Yi(e)=Dwcosαi(e)/Dpw，

式中：ωbs为保持架实际角速度；ωb为假设球纯滚动时保持架理论角速度；ω为内圈角速度；αi，αe分别为内、外圈接触角；β为姿态角。

3.1 转速对轴承打滑特性的影响

当轴向载荷为200 N、径向载荷为0时，通过仿真得到内圈转速分别为5 000，7 000，9 000，11 000，13 000 r/min时的保持架角速度如图6所示，再根据(8)式计算得到不同转速下的保持架打滑率，如图7所示，随转速增大，保持架打滑率增大。这是由于随转速增大，球离心力增大，压向外沟道，与内沟道的接触力变小，球与内沟道的摩擦力随之减小，内圈对球的拖动力减小，球相对内沟道发生打滑，球对保持架的拖动力也会减小，保持架转速增大，最终导致保持架打滑率增大。

图6 不同转速下保持架角速度Fig.6 Angular velocity of cage under different rotational speeds

图7 不同转速下保持架打滑率Fig.7 Slip rate of cage under different rotational speeds

3.2 径向载荷对轴承打滑特性的影响

当轴向载荷为200 N、内圈转速为11 000 r/min时，通过仿真得到径向载荷分别为50，100，150，200，250 N时的保持架角速度如图8所示，随径向载荷增大，保持架角速度也逐渐增大。根据(8)式计算得到不同径向载荷下的保持架打滑率如图9所示，随径向载荷增大，保持架打滑率减小。这是由于球和保持架的运转是依靠内外圈沟道对其产生的拖动力带动，当径向载荷增大时，球与内外圈之间的接触载荷和拖动力均会增大，球对保持架拖动力也会增大，保持架转速增大，保持架打滑率减小。

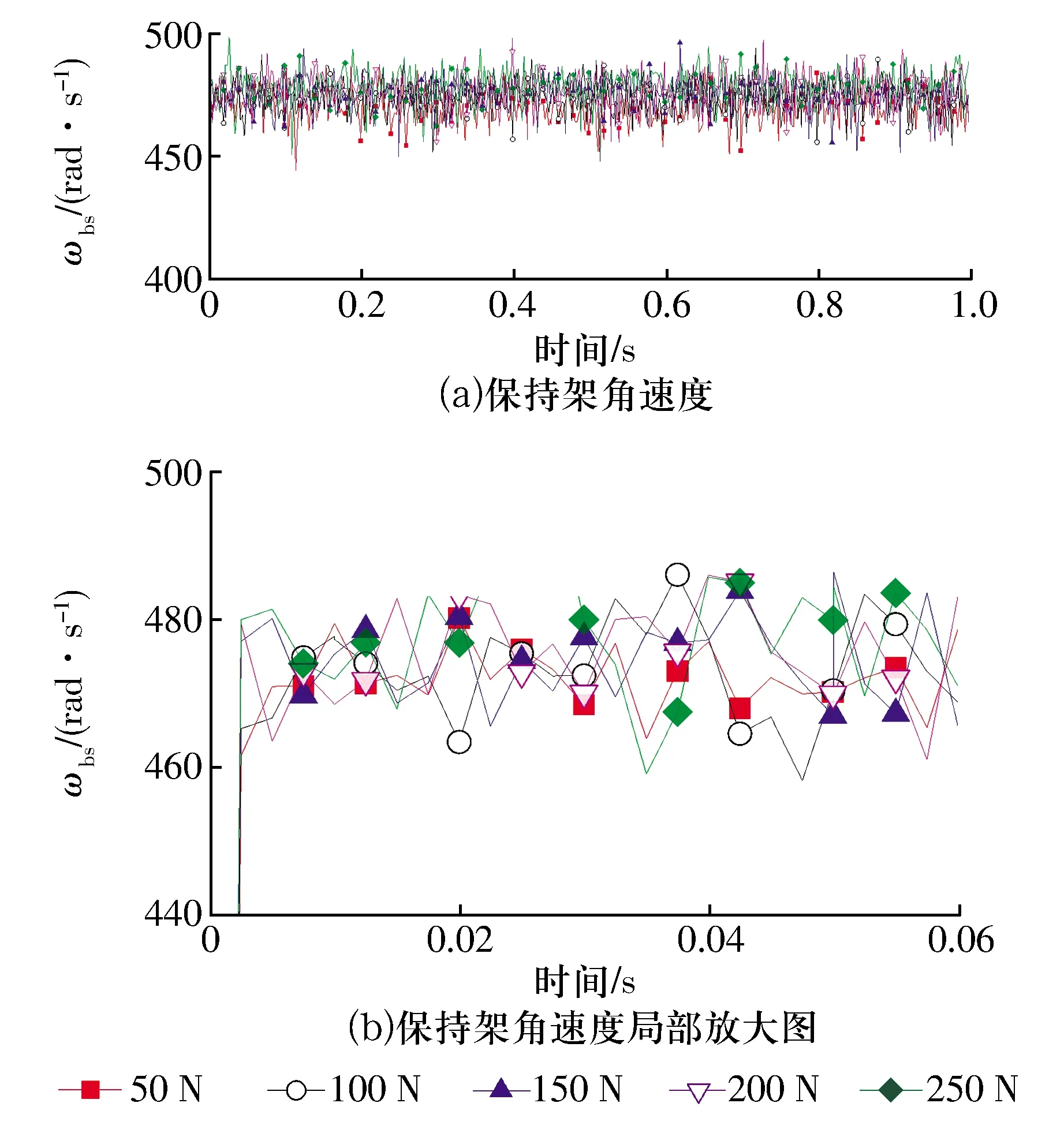
图8 不同径向载荷下保持架角速度Fig.8 Angular velocity of cage under different radial loads

图9 不同径向载荷下保持架打滑率Fig.9 Slip rate of cage under different radial loads

3.3 轴向载荷对轴承打滑特性的影响

当径向载荷为0,内圈转速为11 000 r/min时，通过仿真得到轴向载荷分别为200，250，300，350，400 N时的保持架角速度如图10所示，随轴向载荷增大，保持架角速度也逐渐增大。再根据(8)式计算得到不同轴向载荷下的保持架打滑率如图11所示，随轴向载荷增大，保持架打滑率减小。这是由于球和保持架的运动是依靠球与内外圈沟道之间的拖动力带动，轴向载荷增大时，球与沟道之间接触载荷增大，拖动力也随之增大，使保持架角速度增大，从而使打滑率减小。

图10 不同轴向载荷下保持架角速度Fig.10 Angular velocity of cage under different axial loads

图11 不同轴向载荷下保持架打滑率Fig.11 Slip rate of cage under different axial loads

3.4 小结

径向载荷从50 N增大到250 N时，保持架打滑率从7.21%减小到5.53%，而轴向载荷从200 N增大到400 N时，保持架打滑率从8.19%减小到5.31%。同一转速下，增大轴向载荷比增大径向载荷更有利于减小保持架打滑率，应根据使用工况合理施加轴向载荷和径向载荷。

4 结论

基于赫兹接触理论和弹性流体润滑理论，通过ADAMS多体动力学软件建立了考虑润滑作用下的H7006C角接触球轴承刚柔耦合动力学模型，分析了转速、轴向载荷和径向载荷对角接触球轴承打滑特性的影响，得出以下结论：

1)随转速增大，保持架打滑率增大。

2)随轴向载荷和径向载荷增大，保持架打滑率减小，且打滑率减小幅度不断降低。

3)同一转速下，施加一定轴向载荷相比于径向载荷更有利于减小轴承高速运转下的打滑。