Approximate controllability of fractional order evolution equations with integral impulse conditions
2021-07-21MALinaGUHaiboCHENYiru
MA Lina,GU Haibo,CHEN Yiru
(School of Mathematics Science,Xinjiang Normal University,Urumqi 830017,Xinjiang,China)
Abstract:In the paper,we study a class of fractional evolution equations with integral impulse conditions.By using fixed point theorem and noncompact measure method,we obtain a sufficient condition to ensure the existence of mild solution.A suitable condition for approximate controllability is formulated.Finally,an example is given to explain the reliability of the results.
Key words:fractional order evolution equation;mild solution;approximate controllability;noncompactness measure
1 Introduction
Recently,fractional order evolution equations(FEES)have attracted more and more attention,and have been a valuable tool for modeling many real world dynamic systems[1−3].As we all know,non-local problems are more widely used than classical problems in many areas[4−7].By using Laplace transformation,ZHOU and JIAO[8]first gave the concept of mild solutions to a class of fractional neutral evolution equations.GOU and LI[9]studied the existence of mild solutions to a class of fractional nonautonomous evolution equations.Many practical problems are related to sudden changes in their state,such as catastrophic events,shocks,and heartbeats.This sudden change is called impulse.Sometimes these change stay over a period of time,and these impulses are called noninstantaneous impulses.For many comprehensive studies of non-instantaneous impulsive systems,we can see the papers[10–13].
The concept of controllability is one of the fundamental concepts in mathematical control theory introduced by Kalman in 1960.There are mainly three types of controllability:exact controllability,approximate controllability,and null controllability.Approximate controllability theory of FEES has been widely developed,and some basic results can be found in[14–20].LIU et al[21−22]used iterative learning control(ILC)to give approximate controllability of noninstantaneous impulsive fractional order system.
GE et al[16]studied the controllability of the following fractional order semilinear evolution equations by using approximate solution theory and fixed point theory:
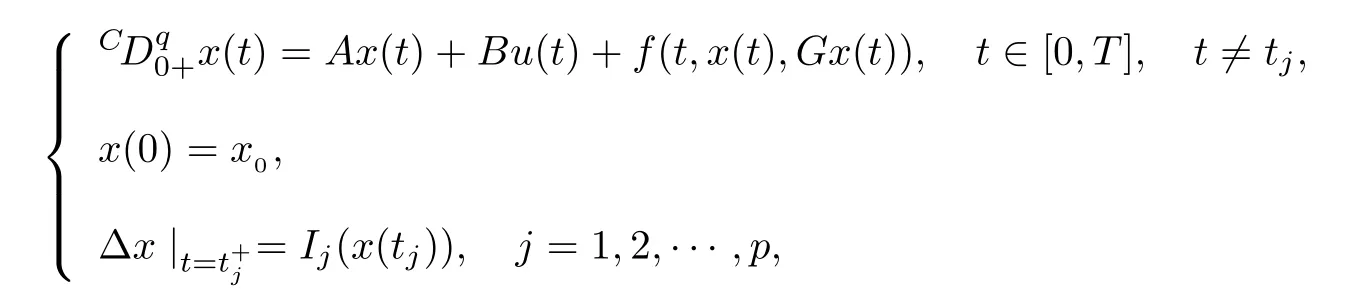
MAHMUDOV[23]studied the approximate controllability and finite-dimensional precise controllability of the semilinear fractional order evolution equation:

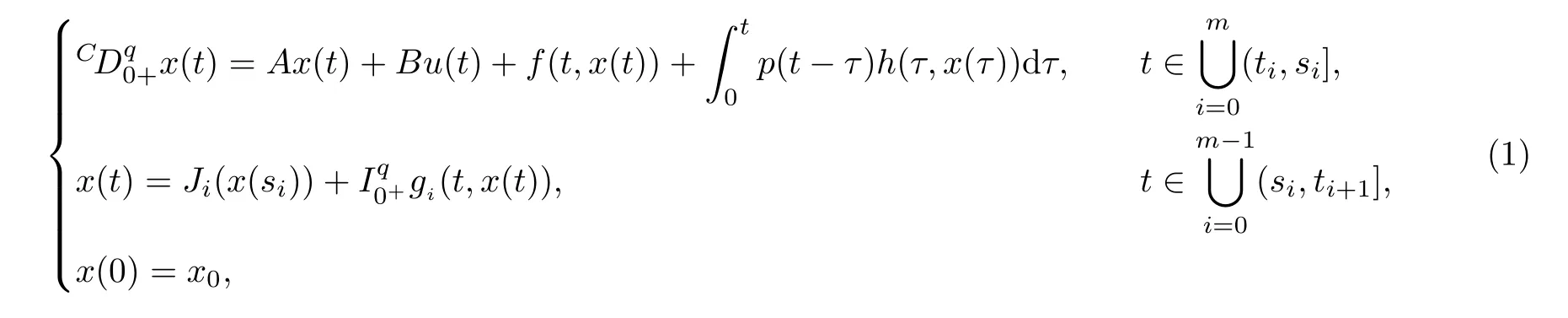
Inspired by the above research,in this paper,we will study the following non-instantaneous fractional evolutionequations with integral impulse conditions:where 0
The motivations of this paper are two aspects.On the one hand,integral equations with fractional integral impulsecondition appear naturally in the fields of biophysics,viscoelasticity,electricalcircuits,etc.WANG[24]obtained existence,uniqueness theorems and stability results for a class of impulsive differential equations.Controllability problem with integral impulse condition is seldom studied.People may ask whether the appropriate solution exists for any given control u and whether the system is approximate controllable.On the other hand,many articles used the fixed point theorem to obtain the approximate controllability of the solution.Rather,in this paper,the approximate controllability of system(1)is discussed by assuming that the linear equation is approximately controllable on the final subintervals(tm,b].
The rest of this paper is organizedas follows.In section 2,some notations and preparationare given.A suitable concept on mild solution for our problem is introduced.In section 3,the existence of mild solutions of system(1)is discussed,and approximate controllability of system(1)is obtained.In section 4,an example is given to explain the validity of our results.
2 Preliminaries

Definition 3[8]If h satisfies a uniform H¨older continuity with exponent β∈(0,1],then the unique solution of the following linear Cauchy problem

Lemma 1[4]The operators S(t)and Q(t)(t0)have the following properties:
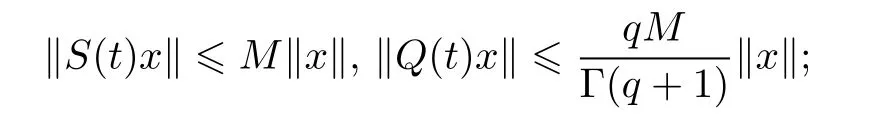
(ii)For every x∈X,t→S(t)x and t→Q(t)x are continuous functions from[0,∞)to X;
(iii)The operators S(t)and Q(t)are strongly continuous in[0,∞).
By[22],we obtained the following definition.
Definition 4For given u∈U,a function x∈PC(I;X)is said to be a mild solution of the system(1),if it satisfies
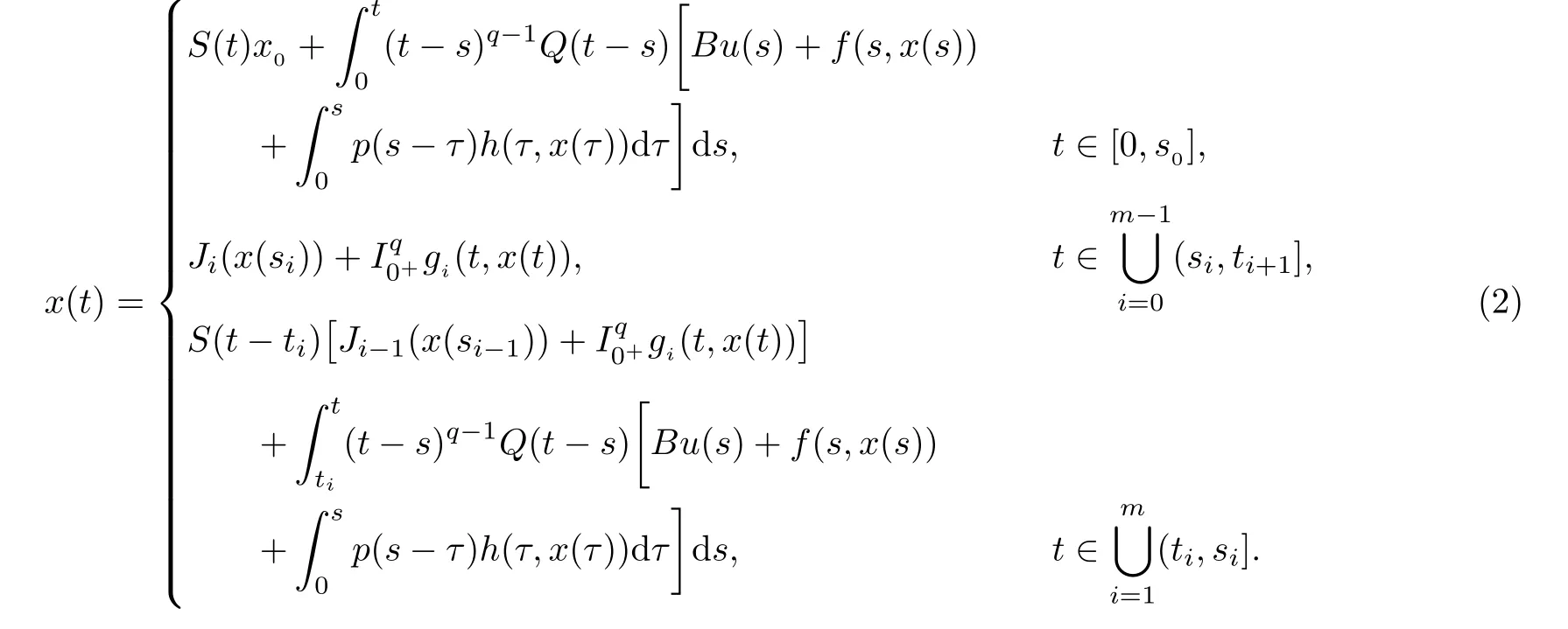
Next,we recall some properties of the measure of noncompactness which will be useful for the proof of our main results.We denote α(·)the KURATOWSKI measure of noncompactness of the bounded sets.For more details about noncompact measure,see[25–26].
Lemma 2[4]For all bounded subsets Ω,Ω1,Ω2of X,the following properties are satisfied:
(1)Ω is precompact if and only if α(Ω)=0;
(3)α(Ω1)α(Ω2)when Ω1⊂Ω2;
(4)α(Ω1∪Ω2)max{α(Ω1),α(Ω2)};
(5)α(lΩ)=|l|α(Ω),for any l∈R;
(6)α(Ω1+Ω2)α(Ω1)+α(Ω2),where Ω1+Ω2={x+y;x∈Ω1,y∈Ω2};
(7)The map Q:D(Q)⊆X→Y is said to be an α-contraction,if there exists a positive constant k<1 such that α(QB) Lemma 3[16]Let X be a Banach space,and V⊂C(I;X),V(t)={v(t):v∈V}(t∈I).If V is bounded and equicontinuous in C(I;X),then α(V(t))is continuous on I,and α(V)=(V(t)). Lemma 4[16]Let X and E be Banach spaces,and Q:D(Q)⊂E→X be Lipschitz continuous with constant L,then α(Q(V))Lα(V)for any bounded subset V⊂D(Q). Lemma 5[16]Let X be a Banach space,and S be a nonempty subset of X.A continuous map Q:S→X is called ρ-set contractive if there exists a constant ρ∈[0,1)such that for every bounded set Ω⊂S,α(Q(Ω))ρα(Ω). Definition 5[21]System(1)is said to be approximatecontrollable on[0,b],if for every x0,xb∈X and ε>0,there exists a control u∈U such that the solution x satisfies x(0)=x0and the inequalityx(b)−xbXε holds. In this section,we will study the existence result of mild solutions of system(1).We also obtain results in the approximate controllability.We first introduce the following assumptions: According to definition 4,the mild solution of system(1)is equivalent to a fixed point of the operator F defined in equation(4).Next,by reference[4],we obtain the existence result of the solution.We will prove that F has a fixed point.Firstly,we obtain In this paper,sufficient conditions for the approximate controllability of a class of fractional evolution equations with integral impulse conditions are considered.By adopting the fixed point theorem and noncompactness measure method,we obtain the existence of solutions and approximate controllability result for fractional evolution equations with integral impulse conditions.In particular,conditions are formulated and proved under the assumption that the linear equation is approximately controllable on the final subintervals.3 Main results


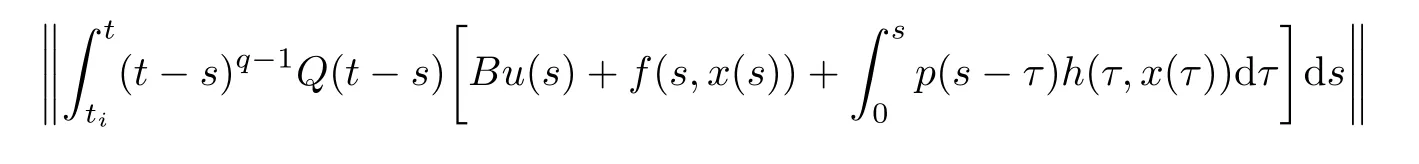







4 An example


5 Conclusion
杂志排行
上海师范大学学报·自然科学版的其它文章
- Multiple rogue wave and multiple lump solutions of a(3+1)-dimensional Korteweg-de Vries equation
- Asymptotic stability of linear multistep methods and Runge-Kutta methods for homogeneous differential-algebraic equations with rectangular coefficients
- A spectral method for Burgers equation using Jacobi polynomial
- A graph-theoretic approach to topology identification of stochastic multi-group models with multiple dispersal
- Reflection ordering in the imprimitive complex reflection group G(m,p,n)
- Anti-periodic solution for fuzzy differential equations
