A spectral method for Burgers equation using Jacobi polynomial

WANG Chenchen,LI Tingting,JIAO Yujian

(Mathematics and Science College,Shanghai Normal University,Shanghai 200234,China)

Abstract:This paper proposes a spectral method for the Burgers equation using Jacobi polynomial.Ample numerical experiments are carried out to validate the efficiency of the new algorithm.

Key words:Burgers equation;spectral method;nonlinear problem;Jacobi polynomial

1 Introduction

Let Λ={y|−∞0 is the kinetic viscosity,f(y,t)and V0(y)are the source term and the initial state,respectively.T is a fixed positive number.The Burgers equation is as following:

where V0(y)→0,∂yV0(y)→0 as y→±∞.

A large number of problems in applied mathematics can be modelled by the Burgers equation.So,it plays a fundamental role in application areas,such as gas dynamics,waves in shallow water,turbulence in fluid dynamics etc[1−6].

There are many scholars who have studied the Burgers equation numerically.Some authors reported the finite difference methods for the Burgers equation[7−9].A number of researchers investigated the finite element approaches for the Burgers equation[10−13].Many authors researched spectral and spectral collocation methods of the Burgers equation[14−17].

In this paper,we propose a spectral method for the Burgers equation by Jacobi polynomial.

2 Preliminaries

In this section,we recall some definitions and relations which will be used in the forthcoming discussion.Let I={x||x|1},α,β>−1 and χα,β(x)=(1−x)α(1+x)β.The Jacobi polynomial of degree l in the interval I is given by

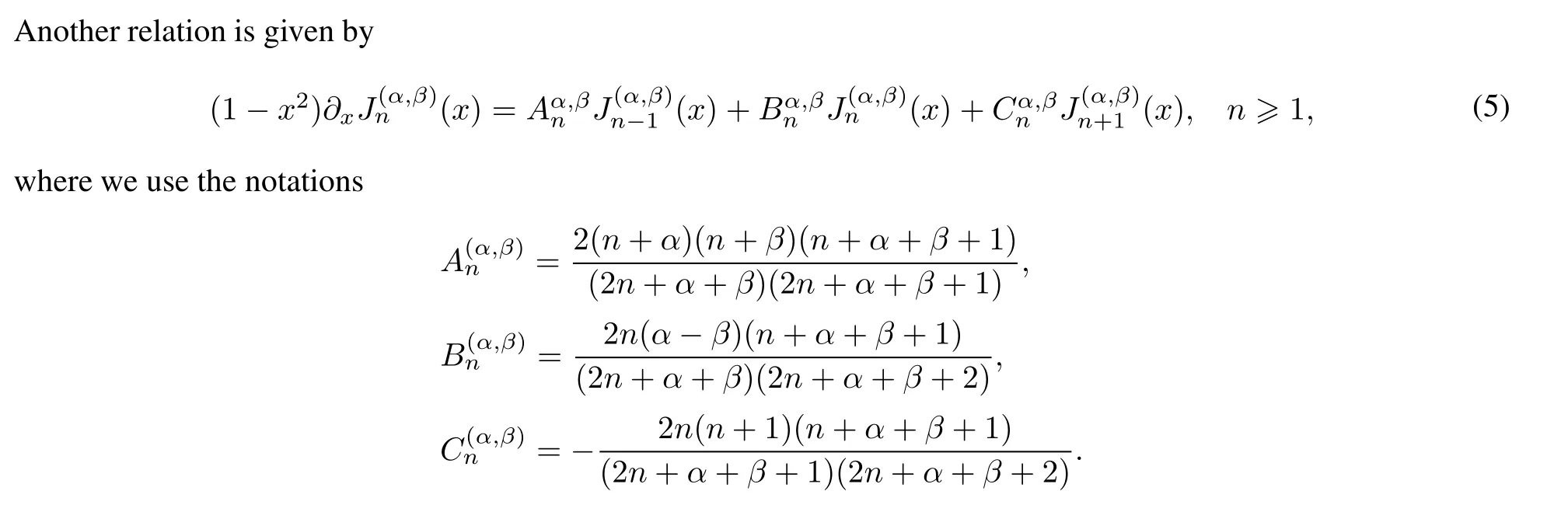
Lemma 1[18]Let f(t)be a non-negativeintegrable functionover(t0,T],and let g(t)and E(t)be continuous functions on[t0,T].If E(t)satisfies

3 Spectral method using Jacobi polynomial

In this section,we propose a spectral method for mapped Burgers equation using the Jacobi polynomial.

The mapping between y∈Λ and x∈I,and its inverse are given by[18]:

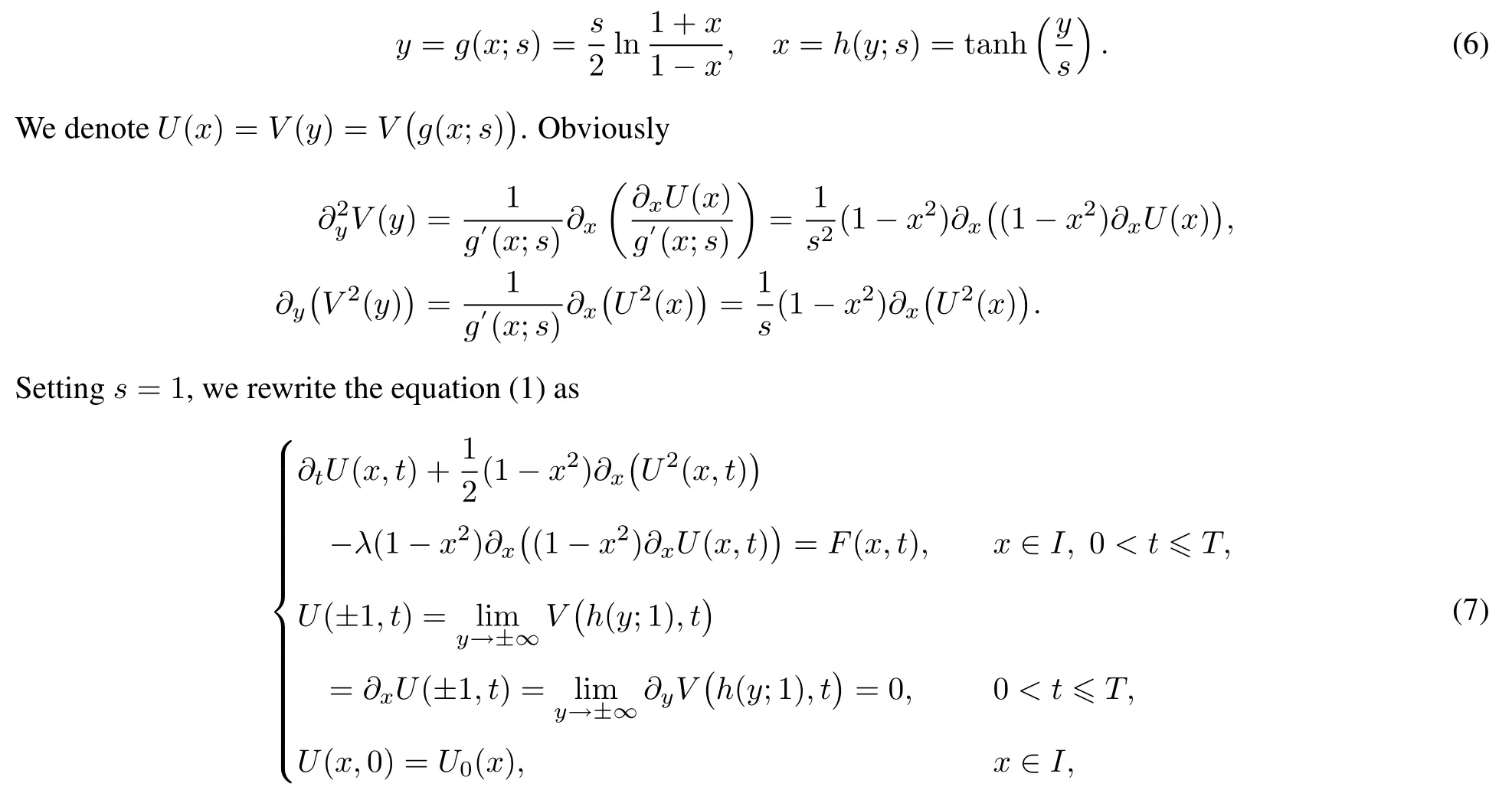
4 Numerical implementation

In this section,we describe details of a numerical implementation,and give some numerical results.

According to(4)and(5)with α=β=2,we derive that

where ξiand ωiare the Jacobi-Gauss nodes and weighs.Then(29)can be written in the following compact matrix form

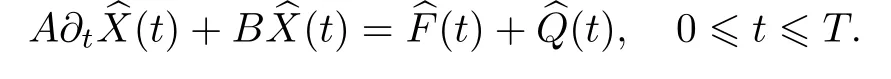
In actual implementation,we use the Crank-Nicolson scheme in time t with the step∆t.The numerical errors are measured by discrete L2-norm

Example 1Take the test function

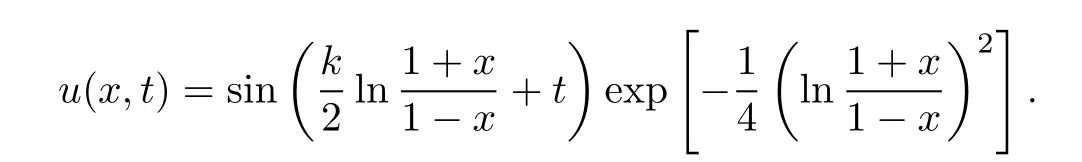
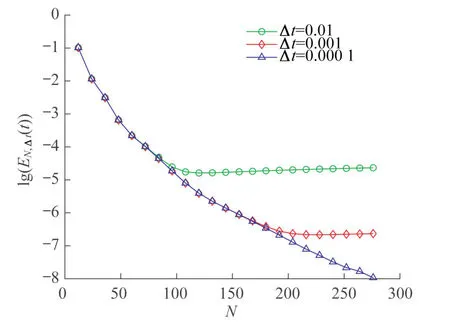
Figure 1 L2-errors against N with λ=1,t=1 and various∆t

Figure 2 L2-errors with λ=1,∆t=0.001 and various t

In figure 1,we plot the errorslg(EN,∆t(t))against modes N with k=2,λ=1,t=1,∆t=0.01,∆t=0.001 and∆t=0.000 1.This shows that the errors decay exponentially.

In figure 2,we sketch the errors lg(EN,∆t(t))with T=100,λ=1,∆t=0.001 and various t.We find that the new proposed scheme is stable for long time computation.

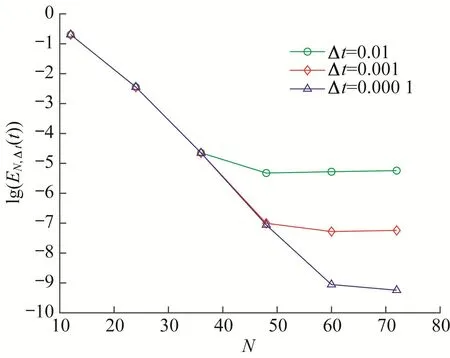
Figure 3 L2-error against N with λ=1,t=1 and various∆t

Example 2Take the test function

In figure 3,we depict the errors lg(EN,∆t(t))against modes N,with λ=1,k=1,t=1,∆t=0.01,∆t=0.001 and∆t=0.000 1.The curves indicate the spectral accuracy in space.

Example 3Take the test function

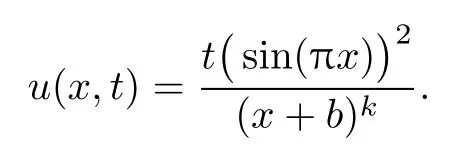
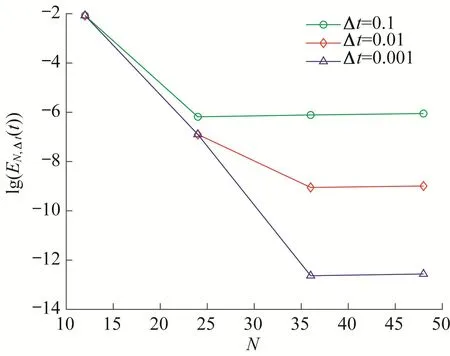
Figure 4 L2-errors against N with λ=1,t=1 and various∆t

In figure 4,we draw errors lg(EN,∆t(t))versus the modes N,with λ=1,k=1,b=2,t=1,∆t=0.1,∆t=0.01 and∆t=0.001.The figure demonstrates high efficiency of the computation.

5 Concluding discussion

In this paper,we studied a spectral method for the Burgers equation using the Jacobi polynomial with parameters α=β=2.We first recalled some definitions and relations of the Jacobi polynomial.Then,we proposed a spectral method to solve the transformed Burgers equation numerically.Numerical results demonstrated the efficiency of this new algorithm.The use of the Jacobi polynomial(x)simplifies the actual computation and brings a sparse system.Then it can be solved efficiently by iteration scheme.