A graph-theoretic approach to topology identification of stochastic multi-group models with multiple dispersal

XIA Dan,ZHANG Chunmei,YAO Xupan,CHEN Huiling

(School of Mathematics,Southwest Jiaotong University,Chengdu 610031,Sichuan,China)

Abstract:In this paper,we investigate topology identification of stochastic multi-group models withmultiple dispersal (SMGMMD).The adaptive observer is designed to identify multiple topological structures of SMGMMD based on adaptive synchronization method.By using Lyapunov stability theory and graph-theoretic approach,we provide some criteria to successfully identify the unknown topological structures of SMGMMD with and without time delay.Finally,topology identification of coupled Lorenz systems with and without time delay are given to illustrate the availability of proposed results.

Key words:topology identification;graph-theoretic approach;multi-group models;synchronization

1 Introduction

In recent years,many researchers pay more attention to the dynamics of multi-group models,due to their widespread use in epidemiology,ecological areas and other fields[1−6].There are many results about multi-group models[7−13].For a better description of the real-world systems,multiple dispersal among groups and stochastic perturbations are considered into multi-group models to get stochastic multi-group models with multiple dispersal(SMGMMD).Researchers have obtained many results about SMGMMD[8,14−17].Therein,most researchers have investigated the dynamics of SMGMMD based on given topological structures.For example,in[8]and[15],GUO et al have shown the input-state stability of stochastic diffusion multi-group networks with and without time delay.However,the topological structure is often unknown(uncertain)or partially unknown in practice.Hence,it is necessary to identify topological structures of multi-group models.

In the literature,some researchers focus more on topology identification of networks[18−29].They usually useadaptive synchronization method to study topology identification of single network[19−23].Other researchers have investigatedtopology identification of multiple networks by using compressed sensing[24−25]or adaptive synchronization[26−29].There exist few results about topologyidentification of multiple dispersal networks in multigroup models.

Based on the above discussion,this paper attempts to identify topological structures of SMGMMD based on adaptive synchronization.By the method of network split,SMGMMD can be split into multiple sub-networks,in which each sub-networkhas the same kind of dispersal.There exist multiple topological structures of networks to be identified.The key point is to construct appropriate Lyapunov function.However,multiple dispersal among groups and stochastic perturbation makes it difficult to construct Lyapunov function for SMGMMD directly.So,this paper tends to use graph-theoretic method to construct it indirectly[30−35].Based on Kirchhoff’s Matrix-Tree Theorem,Lyapunov function of this model can be obtained by weighted summation of Lyapunov function of each group.

The contributions of this paper are threefold.Firstly,the model is much more reasonable in real applications,in which multi-dispersal and white noise are all considered into multi-group models.Secondly,by using the driveresponse concept and graph-theoretic method,we construct a Lyapunov function indirectly for the error system of drive-response system.Thirdly,the appropriate adaptive controller is designed in response system.When driver esponse system achieves synchronization,multiple topological structures of drivesystem are successfully identified.

The rest of this paper is arranged as follows.In section 2,preliminaries are introduced.Based on adaptive synchronization,sufficient identification criterion for multiple topological structures of SMGMMD are provided in section 3.In section 4,a numerical simulation is reported to illustrate analytical results.Finally,some conclusions are provided.

2 Preliminaries

We write C2,1(Rn×R+;R+)for the family of all nonnegative functions V(x,t)on Rn×R+that are continuously differentiable twice in x and once in t.Define a diffusion operator L acting on V∈C2,1(Rn×R+;R+),

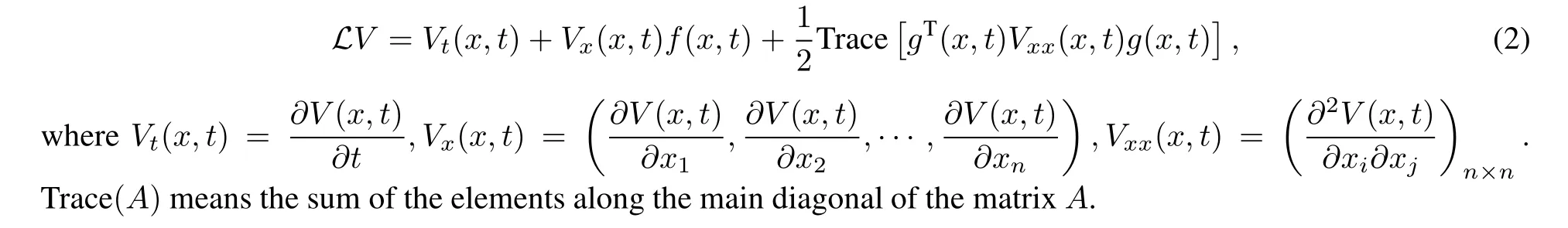
The following two important lemmas will be used in our proof.

Lemma 3(Theorem 2.1 in[36])Assume that there is a function V ∈C2,1(Rn×R+;R+),a function γ∈L1(R+;R+),and a continuous function φ:Rn→R+such that

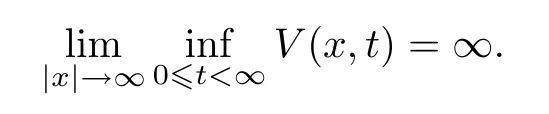
Assume the diffusion operator L acting on V along with the trajectories of(1)satisfies

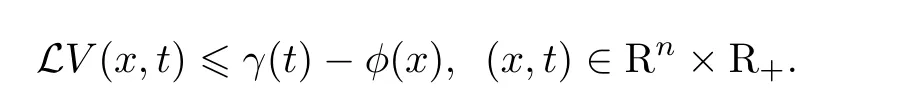
Furthermore,assume that g is bounded.Then,for every initial value x0∈Rn,exists and is finite almost surely.Moreover,

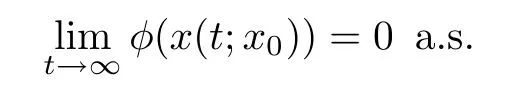
Now we consider an n-dimensional stochastic differential equation with delay

3 Main result

In this section,we are going to investigate the problem of SMGM,which is described as a coupled system on multi-network.Suppose that there are l individual groups or patches.In each group,there are s components.Then,we take s×l vertices to denote s×l dynamical systems and connect them by s dispersal networks.Two theorems with respect to topology identification of SMGMMD with or without delay are presented.

3.1 Topology identification based on adaptive synchronization

In this subsection,we mainly study topology identification of SMGMMD without delay.Adaptive synchronization method,graph theoretic method and Lyapunov theory are used to identify unknown topological structure.

The drive system of SMGMMD can be described by the following equations:

Through this paper,for any given initial values e0∈Rm×l,we denote the unique solution of(7)as e(t;t0,e0).In most cases,we write e(t;t0,e0)as e(t)for simplicity.

The adaptive controller and updating law are designed as

Remark 2In[7–8,13,15–16],they study the dynamics of multi-group models with multiple dispersal based on known dispersal networks.In fact,topological structures of multiple dispersal systems in real applications are always unknown.So,it is necessary to identify them.Based on graph-theoretic method and adaptive control technique,we successfully identify the topological structures of multiple dispersal networks.Thus the work of this paper is significant.

There are many results about the topology identification of single network based on adaptive synchronization method[19−23].But this paper identifies the topological structures of multiple dispersal networks,which is different from the literature results.There exist few papers about the identification of multi-layer networks by compressed sensing[24−25]or adaptive synchronization[26−29].But this paper combines graph-theoretic method and adaptive synchronization to get the identification of multi-groupmodels with multi-dispersal and stochastic perturbation.The research method is novel and different from[24–29].

3.2 Topology identification based on adaptive synchronization with time delay

Time delay is an inevitable factor that cannot be ignored because it may promote the generation of bad dynamical behavior.Many practical systems can not avoid its influence.Therefore,in order to better reflect the essential characteristics of SMGMMD,we must consider time delay.In this subsection,we are going to investigate topology identification of SMGMMD with time delay.Each diffusion network considers different time delay.This subsection uses adaptive synchronization method,graph theoretic method and Lyapunov theory to study topology identification of SMGMMD with time delay.

First,we define the drive system of SMGMMD with time delay,

Remark 3[19]WU et al have studied topological structure of stochastic single-weighted complex dynamical networks with and without delay.But this paper investigates SMGMMD with and without time delay,which is different from[19].Moreover,the graph-theoretic method is used in this paper that is totally different from their method.In all,the model and method in this paper are different from[19].YAO et al[39]aim to identify the topological structures of multi-weighted complex networks with and without time delay based on adaptive synchronization.This paper investigates topology identification of stochastic multi-group models with multiple dispersal.The model is totally different from the model in[39].

4 Numerical examples

In this section,coupled Lorenz systems with and without time delay are identified to demonstrate the feasibility and effectiveness of our theoretical results.

We consider a typical benchmark chaotic system:Lorenz chaotic system.There are six groups and each group has three components.Each component disperses among six groups.

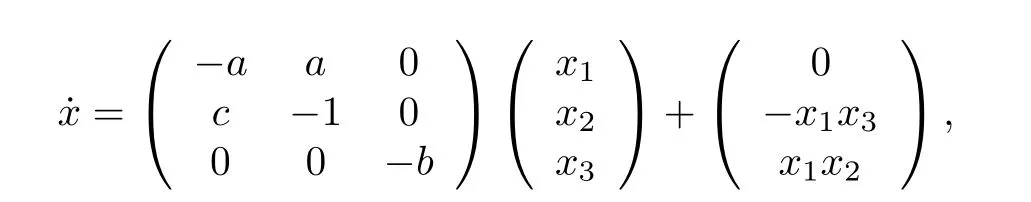
where a=10,b=8/3,c=28.

Example 1We consider a complex system with three weights and six nodes as a drive system without time delay:

Then in order to synchronize this system via feedback control,the response system with stochastic perturbation can be designed as(k=1,2,···,6):

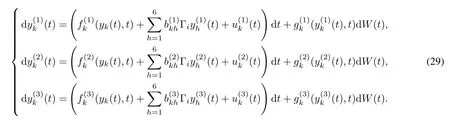
Lorenz system satisfies(A1).For details,please refer to reference[40–41].Here(i=1,2,3,k=1,2,···,6)are trigonometric functions,so they obviously satisfy(A2).According to the theorem 1,drive-response systems(28)and(29)achieve synchronization and diffusion matrices A(i)=,i=1,2,3 can be estimated by matrices B(i)=, i=1,2,3 under the following controllers and update law.

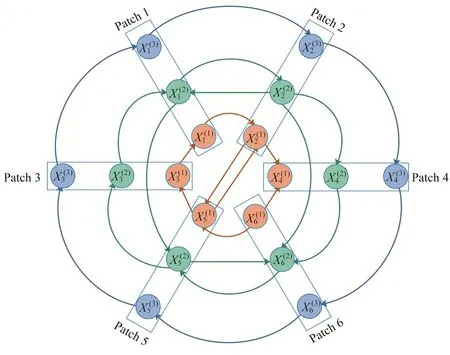
Figure 1 Topological structure of weighted graph in(28)

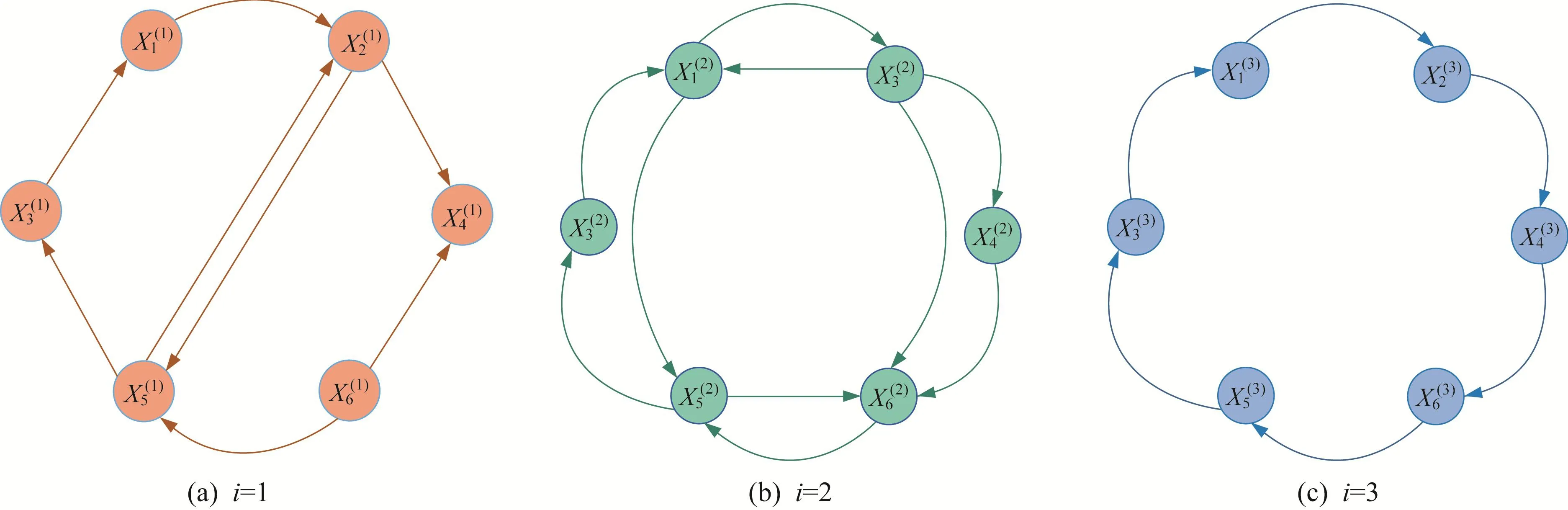
Figure 2 Topological structures of weighted subgraphs(G,A(i)),i=1,2,3

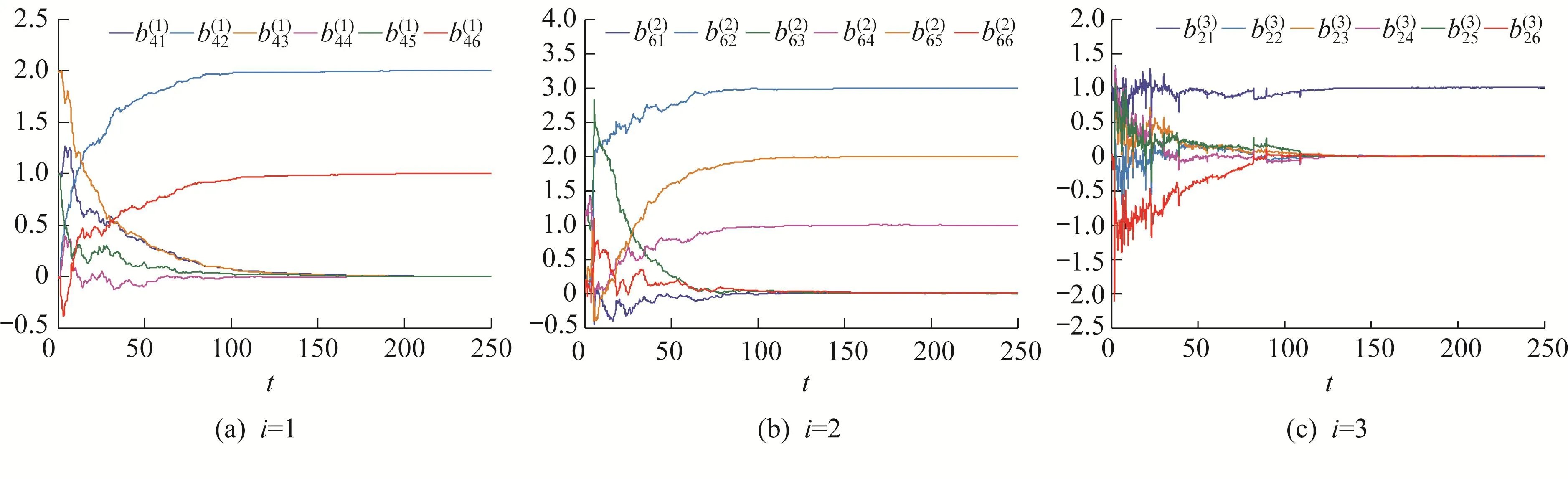
Figure 3 Identification of partial coupling configuration matrices()6×6(k,h=1,2,···,6;i=1,2,3)in model(28)

Figure 4 Sample path of synchronization error for drive-response systems(28)and(29)

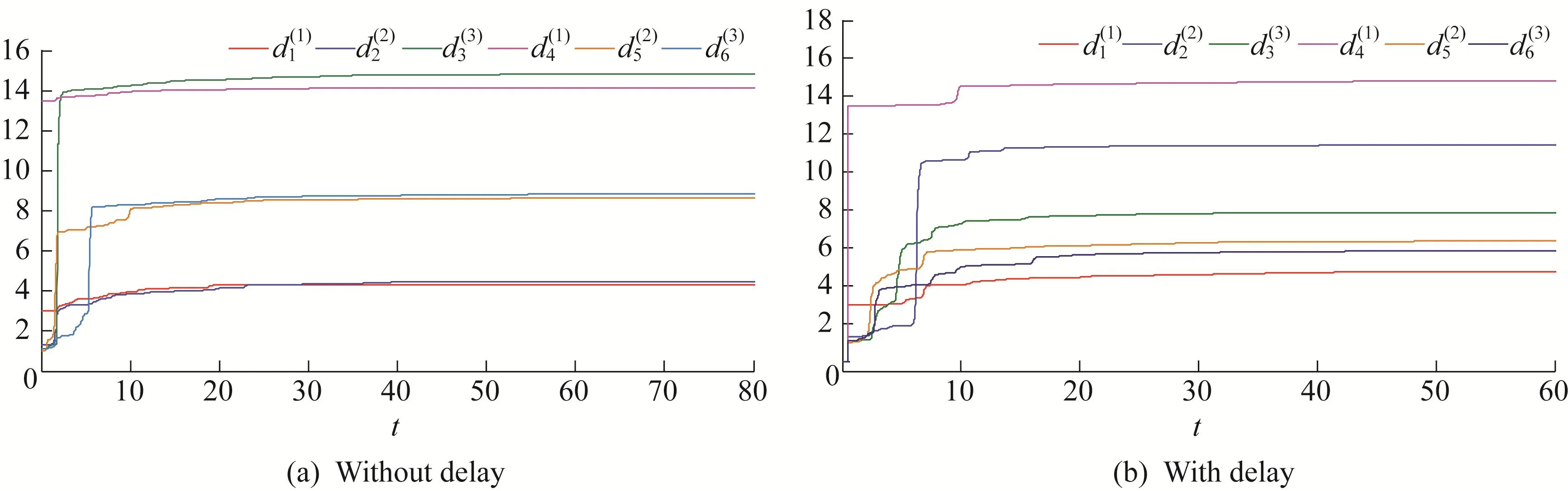
Figure 5 Feedback gains varying with time t

Example 2Consider the drive system(28)with constant delay τ1=0.2,τ2=0.4,τ3=0.5.The drive system with delay can be described as(k=1,2,···,6):

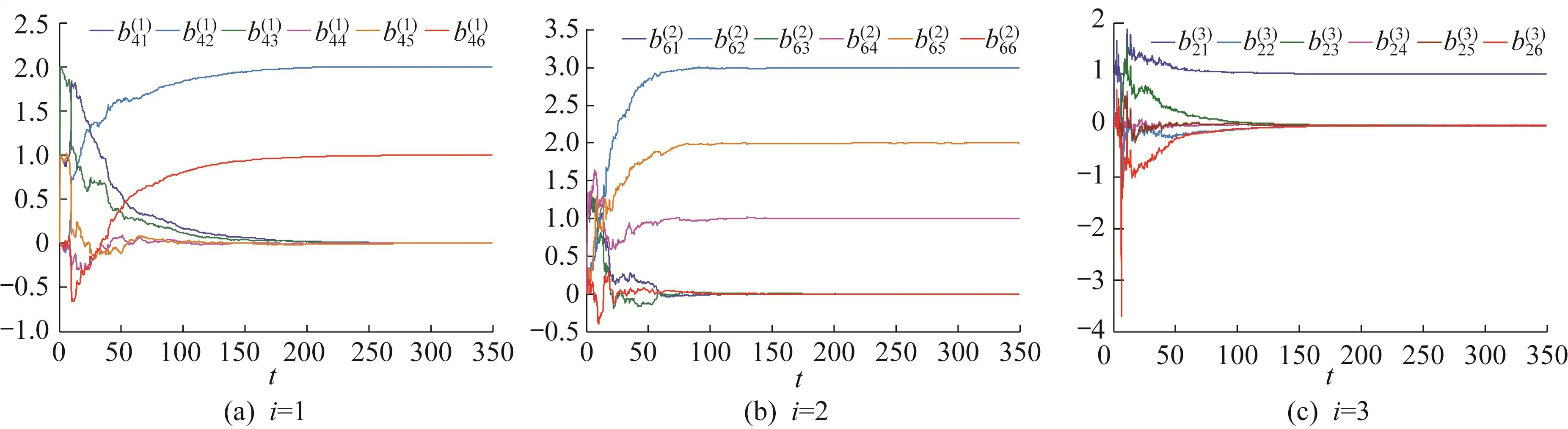
Figure 6 Identification of partial coupling configuration matrices()6×6(k,h=1,2,···,6;i=1,2,3)in model(30)

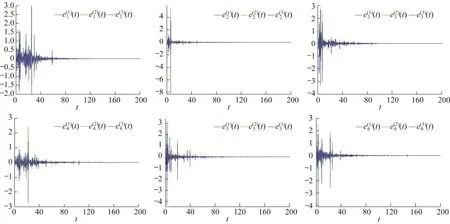
Figure 7 Sample path of synchronization error for drive-response systems(30)and(31)

4 Conclusions

In this paper,topology identification of SMGMMD with and without time delay are studied based on adaptive synchronization.The key point is to construct global Lyapunov function for SMGMMD by using graph-theoretic method.By combining stochastic analysis and control theory,drive-response systems achieve synchronization under the appropriate adaptive controller.Meanwhile,the unknown multiple topological structures in the drive system are identified successfully.Topology identification of coupled Lorenz systems are also shown to illustrate the effectiveness of our theoretical results.In future,we will study the partial topology identification of SMGMMD.