Anti-periodic solution for fuzzy differential equations

ZHU Shumin,WANG Qi

(School of Mathematical Sciences,Anhui University,Hefei 230601,Anhui,China)

Abstract:In this paper,using differential inclusions’approach,we obtain existence results of antiperiodic solutions for a class of fuzzy differential equations.An example shows the feasibility of the main results.

Key words:fuzzy differential equations;differential inclusions;anti-periodic solutions

1 Introduction

Differential inclusions is an important tool to investigate fuzzy differential equations[1−2].In[3],the authors considered the periodic solutions to first order fuzzy differential equations using differential inclusions’approach.Motivated by[3],we consider the T-anti-periodic solutions to fuzzy differential equations

where 0∈I(a real interval);y0and b(t)∈RF(will be defined later),a(t)∈R(the set of all real numbers)for all t∈I and a,b are continuous on I.More results on boundary value problems and periodic solution for fuzzy differential equations,see[4–13]for details.More details of anti-periodic boundary problems and anti-periodic solutions,see[14–18]for details.

2 Preliminaries

Definition 1[19]Let the set X∅.A fuzzy set u on X is characterized by its membership function u:X→[0,1].Thus for each x∈X,u(x)is the degree of membership of the element x to the fuzzy set u.

The space of fuzzy numbers denoted by RFis defined as the class of fuzzy subsets of the real axis R,i.e.u:R→[0,1]such that

Consider the first order linear ordinary differential equations

where 0∈I,a,b:I→R are both continuous and c∈R.

Definition 4The solution to(2)is

It is said to be the T-anti-periodicif x(t)=−x(t+T)for t,T,t+T∈I,T>0.

About the condition x(0)+x(T)=0,we have the following lemmas.

Lemma 1The function in(3)satisfies the condition x(0)+x(T)=0 if and only if

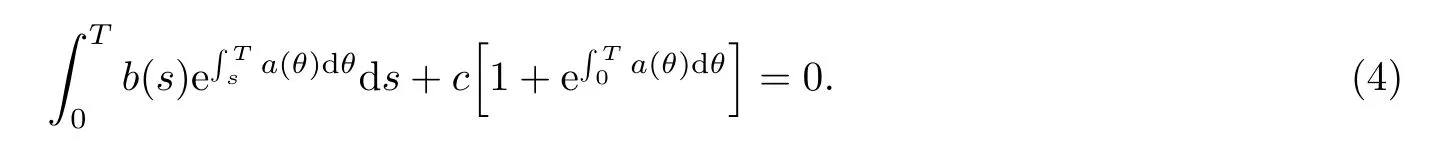
Lemma 2If a(t)is T-periodic,b(t)is T-anti-periodic,then(3)satisfies x(t)+x(t+T)=0.Furthermore,equation(2)has a unique T-anti-periodic solution provided that(4)holds.

ProofBy(2),a(t)=a(t+T),b(t)+b(t+T)=0.It follows that

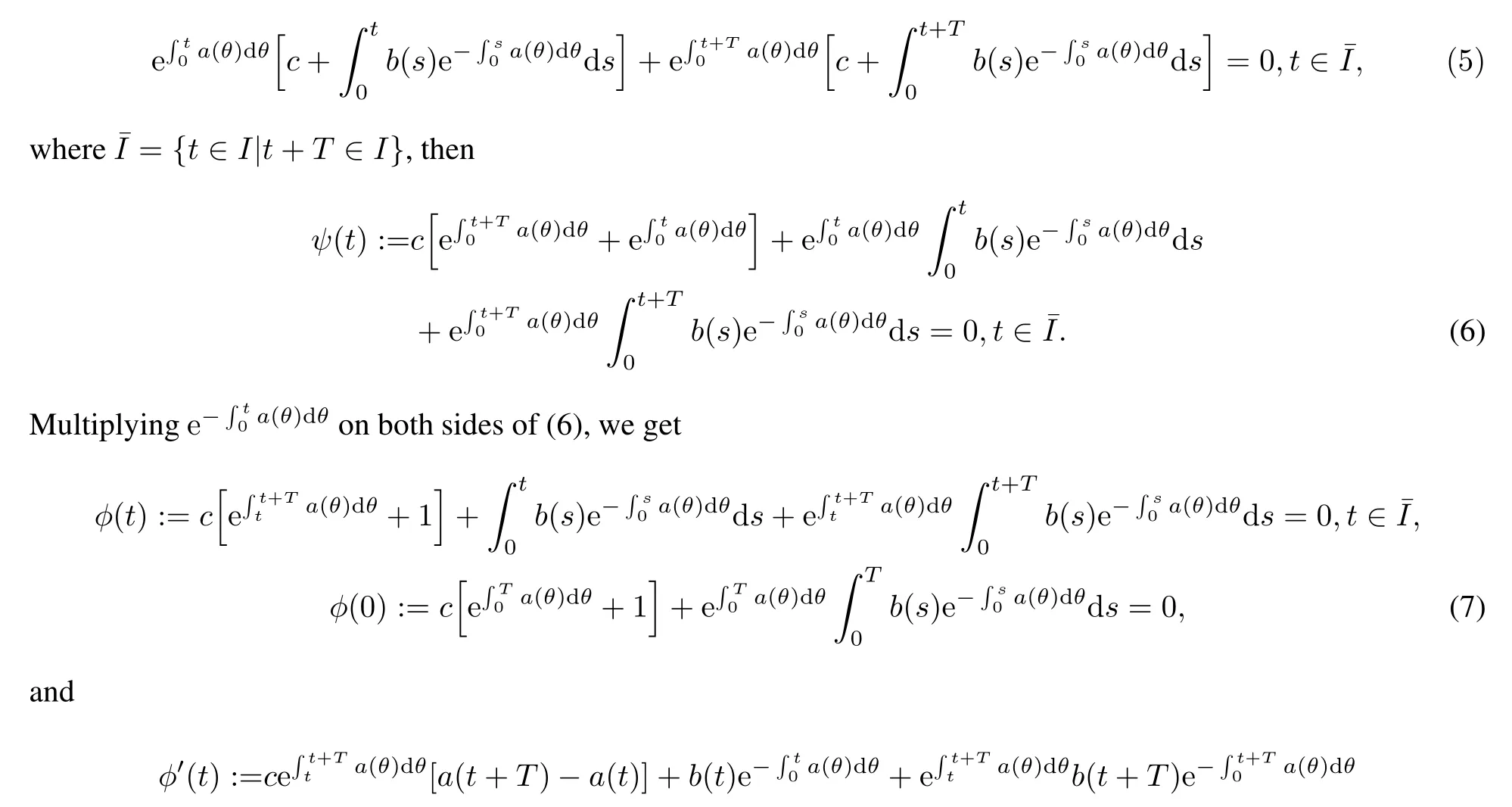
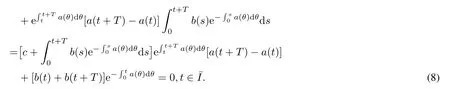
Since the above process is reversible,so x(t)+x(t+T)=0,t∈holds.

From lemma 1,lemma 2,it follows the next lemma.

Lemma 3Let the function x in(3)be T-anti-periodic.Then

(a1)The equality(4)holds.

(a2)c(a(T)−a(0))=b(T)+b(0).Furthermore a(T)=a(0)implies that b(T)=−b(0).

(a3)b(t)is T-anti-periodic provided that the function a(t)is T-periodic.

(a4)x is independent of a(t)provided that c=0,b=0.

(a5)a(t)is T-periodic provided that c0,b=0.

Proof(a1)If x is T-anti-periodic,then x(0)+x(T)=0 and(4)holds by lemma 1 naturally.

(a2)If the function x in(3)is T-anti-periodic.Let t=0 in(8),then

The proof of(a3),(a4),(a5)can be derived from(8)easily.

3 Main results

Following the method in[1],we only consider this fuzzy differential inclusion

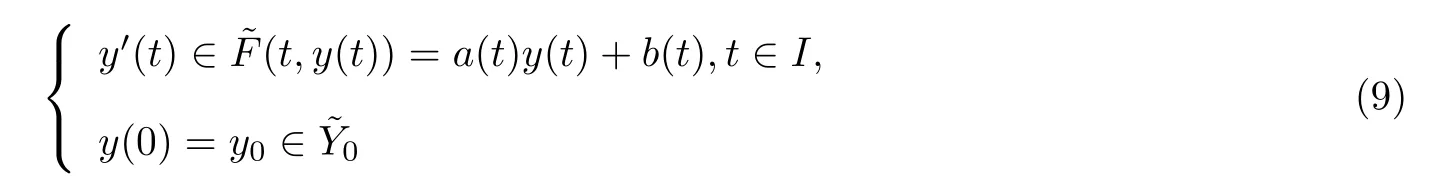
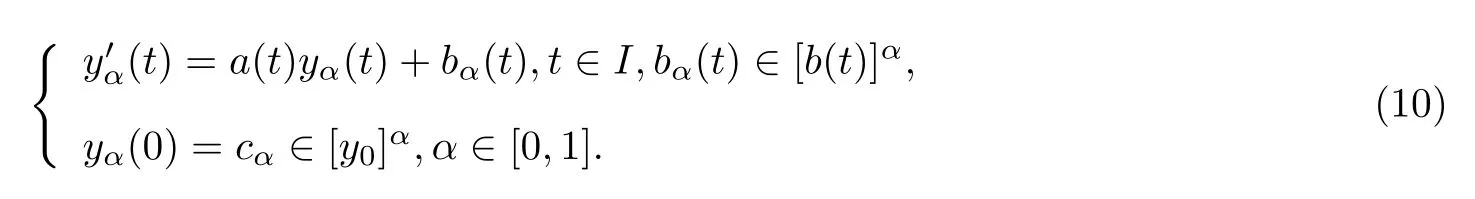
Then problem(9)can be understood as the α-level family of differential inclusions(10).

Definition 5[1]A function y(t):I→Rnis said to be an α-solution to(9)on the interval I if it is a solution to(10)for α∈[0,1].

Definition 6The following set is called the attainable set of the α-solution at t∈I,

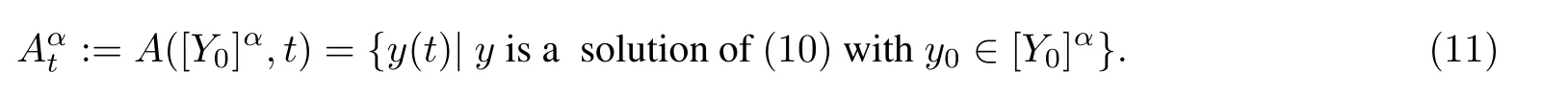
From(10),it follows that

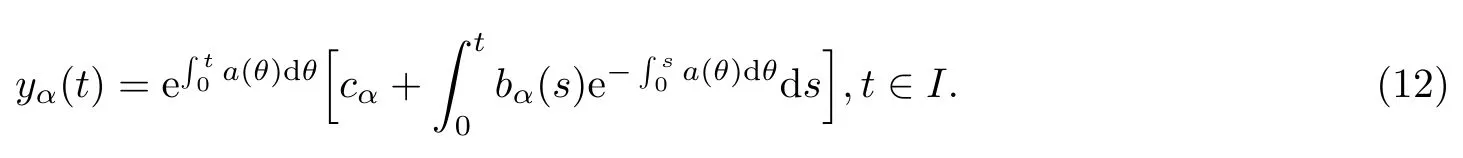
Using the nondecreasing property of yα(t)in cαand bα,then we get

where Dα(t)denotes the diameter of the attainable sets Aα(y0,t)at t∈I.

Replacing b(t),c by diam([b(t)]α),diam([y0]α)respectively,and using the method as lemma 2,we get

Theorem 1Assume that a(t)is T-periodic,diam([b(t)]α),α∈[0,1]is T-anti-periodicand

then the function Dα(t)in(14)is T-anti-periodic in t∈I,α∈[0,1].

Theorem 2If a(t)is T-periodic,then Aα(y0,0)+Aα(y0,T)=0,α∈[0,1]if and only if

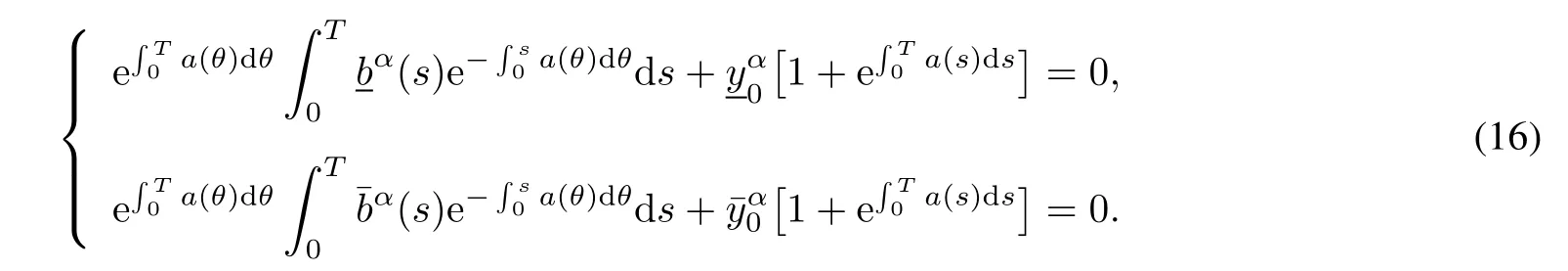
ProofIf a(t)is T-periodic and Aα(y0,0)+Aα(y0,T)=0.Then the solutions to the following problems

satisfy y(0)+y(T)=0,which implies(16)by lemma 1.From(16)and lemma 1,the solutions to(17)satisfy the boundary condition y(0)+y(T)=0.Thus the same conclusion can be deduced for Aα(y0,t),t∈I,α∈[0,1].

Theorem 3Assume that a(t)is T-periodic,b(t)is T-anti-periodic with(16)hold.Then the solution to(1)under differential inclusions approach(the solution to(9))is T-anti-periodic.

ProofFor any α∈[0,1],replacing c,γ(t)byrespectively,using theorem 2 and a(t)=a(t+T),b(t)+b(t+T)=0,we see that the T-anti-periodicity of the functions

in t,which coincides with hypothesis(16)and the conclusion is obtained.

Theorem 4Let the solution to(1)be T-anti-periodic.Then

(b1)Condition(16)holds.

(b2)If a(t)is T-periodic,then b(t)is T-anti-periodic.

(b3)If y0=b=χ{0},then the solution of(1)is T-anti-periodic independently of a(t).

(b4)If A0(y0,t),[b(t)]0are T-anti-periodic and A0(y0,t)={0}for a.e.t∈I,then a(t)is T-periodic.

(b5)If b is T-anti-periodicand A0(y0,t)={0}for a.e.t∈I,then a(t)is T-periodic.

on J and A0(y0,t)={0}on J.This contradicts with A0(y0,t){0}for a.e.t∈I.

(b5)This holds by the conclusion in(b4).

Considering the T-anti-periodicity of the midpoint of the α-attainable set at time t,we get

then the function Mα(t)is T-anti-periodic in the variable t∈I,α∈[0,1].

ProofSimilar to the proof of theorem 1,we replace b(t)and c by mp([b(t)]α)and mp([y0]α)respectively.Then theorem 5 holds by lemma 2.

Theorem 6Let a(t)be T-periodic,then the interval-valued function

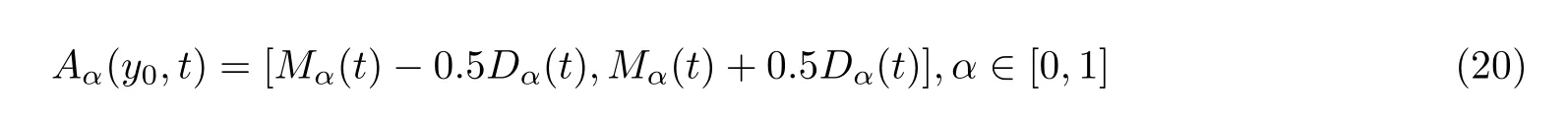
is T-anti-periodic if and only if the functions Mα(t),Dα(t)are both T-anti-periodic.

In the following part,let I=[0,+∞).By(20),we have the following results.

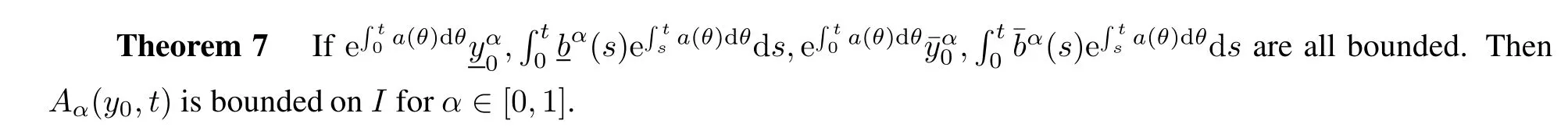
4 Example

Consider the following first order fuzzy differential equation:

where γ,δ∈RFare given by[γ]α=[α+1,3−α],[δ]α=[0.5α+1,2−0.5α],α∈[0,1].Then by theorems 1 and 3,the function Dα(t)is T-anti-periodicand the solution is T-anti-periodicsolution with T=π.